

| Es la
inversa del muestreo. Una vez que el ordenador ha analizado o efectuado un control
sobre la señal discretizada se tiene que devolver una salida continua. Para
ello se hace necesario reconstruir la señal. El radio de acción de un
reconstructor esta entre muestra y muestra. |
| Entre
muestra y muestra se pueden hacer múltiples cosas, desde mantener la señal,
hasta con una función polinómicas tratar de acercarse más a la señal continua
deseada. Como es lógico, cuanto más complejo es el polinomio, más se tarda en procesar
todos los datos, y la señal continua tarda más en crearse. |
| Se
clasifica a los diferentes tipos de reconstructores, según su complejidad en el
polinomio más sencillo. |
| Un
reconstructor ideal es imposible dado que, modelando matemáticamente el reconstructor,
obtenemos que seria un filtro no causal, es decir, dependeria de entradas
futuras, lo cual, en la realidad es imposible. |
| Ahora bien, si existen reconstructores sencillos y que logran hacer una aproximación bastante buena de la señal continua que deseamos. Brevemente vamos a analizar dos: el retenedor de orden cero y el retenedor de primer orden. |
Retenedor de orden cero |
| El retenedor de orden cero es el más sencillo de los reconstructores. Su funcionamiento se basa en mantener constante la señal entre muestra y muestra. Es el más usado por su sencillez, y porque además suele venir incluido en los convertidores analógico-digital. Además este reconstructor tiene la ventaja extra de que se puede utilizar en sistemas con muestreo no periódico. También al ser tan sencillo, y como ya hemos mencionado, tarda menos en construir la señal continua y es el más rapido. |
| En los ejemplos podemos ver como se crea
una serie de bloques como función del resultado de arrastrar el valor de cada
muestra hasta la siguiente muestra. La función de transferencia de este
retenedor seria la siguiente: |
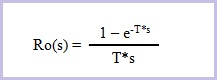 |
Retenedor de primer orden |
| El
retenedor de primer orden es menos utilizado que el retenedor de orden cero,
con lo que no entraremos en tantos detalles con él. El retenedor de primer
orden se basa en obtener la derivada en la muestra exacta, calcular su
pendiente y entre muestra y muestra crear una recta con la pendiente obtenida
anteriormente. |
| La función de transferencia del retenedor de primer orden seria la siguiente: |
|
|
| Como vemos la formula del retenedor del primer orden, es igual que la del retenedor de orden cero, solo que se le suma una recta con una derivada. Eso coincide con la definición del retenedor de primer orden: la derivada de la curva que pasaria por la muestra para obtener la pendiente y hacer una recta a partir de esa muestra hasta la siguiente muestra y así conseguir aproximarse a la tendencia que tendria la curva real. |
| Existen
más tipos de retenedores y más precisos. Un ejemplo seria el retenedor
poligonal. Dicho retenedor entre muestra y muestra crea una línea entre cada
muestra. Es mucho más preciso, pero por contra es más lento. |
| En conclusión nos quedaremos mejor con el retenedor de orden cero, dado que aunque es peor reconstruyendo la señal, es el más rápido y el más sencillo. |
 |
 |
 |