2 Análisis de datos de dos variables

2.1 Introducción.

En el capítulo anterior estudiamos las principales medidas utilizadas para describir una caractarística, una variable. En este capítulo vamos a considerar que estamos interesados en analizar dos características/variables de los individuos/observaciones.

Cuando consideramos dos variables podemos trabajar con cada una de ellas por separado (análisis unidimensional o de una variable: es de aplicación todo lo visto en el capítulo anterior) y con las dos variables conjuntamente (análisis bidimensional). En esta última situación nos preguntaremos, por ejemplo, si las variables consideradas están relacionadas entre sí y, en su caso, cómo es la fortaleza o intensidad de dicha relación. Como se trata de un curso introductorio, nos centramos en el caso más sencillo, aquél en el que la relación entre las variables es de tipo lineal.

Tabla 2.1: Datos de una muestra de 15 empleados de una gran compañia.

Empleado	Experiencia (variableX)	Salario (variableY)
1	4	1,400
2	2	1,200
3	3	1,200
4	4	1,300
5	2	1,300
6	4	1,400
7	2	1,200
8	2	1,200
9	3	1,300
10	4	1,400
11	4	1,400
12	3	1,300
13	2	1,200
14	4	1,400
15	3	1,300

Vamos a introducir la notación que utilizaremos en el resto del capítulo a través de un ejemplo. Supongamos que en una gran empresa se seleccionan aleatoriamente 15 trabajadores que trabajan en el mismo departamento. Sobre esta muestra de empleados estamos interesados en estudiar la posible relación entre el salario bruto mensual (en euros) y el número de años experiencia en la empresa. Recogemos los datos relativos a estas dos variables en la Tabla 2.1.

Como ahora sobre cada individuo u observación (los trabajadores) estamos interesados en analizar dos características (X: experiencia, Y: salario mensual), la Tabla 2.1 es una representación de una variable estadística bidimensional (X,Y). Esta forma tabular es la habitual en la que encontraremos los datos; y es la estructura sobre la que los tratamos cuando utilizamos el ordenador.

La variable X puede tomar I valores distintos ($x_i$ con $i=1,2,...,I$) y la variable Y puede tomar J valores distintos ($y_j$ con $j=1,2,...,J$). Siguiendo con el ejemplo, y como vemos en la Tabla 2.1, tenemos:

un total de n observaciones ($n=15$).
un total de 15 pares de datos ($x_i,y_i$) con $i=(1,2,..,15)$.
la variable X toma 3 valores distintos ($I=3$), que ordenados de menor a mayor son:
$x_1=2,\thinspace x_2=3,\thinspace x_3=4$
la variable Y también toma 3 valores distintos ($J=3$), ordenados de menor a mayor:
$y_1=1,200,\thinspace y_2=1,300,\thinspace y_3=1,400$

Recordad, si trabajamos con una muestra, el número de observaciones se presenta por n (tamaño de la muestra); si trabajamos con la población, el número de observaciones se representa por N (tamaño de la población).

2.2 Distribuciones de frecuencias bidimensionales.

En este apartado vamos a introducir los tipos de distribuciones de frecuencias con las que habitualmente se trabaja cuando tenemos dos variables: las distribuciones de frecuencias conjuntas, las distribuciones de frecuencias marginales y las distribuciones de frecuencias condicionadas.

2.2.1 Distribución de frecuencias conjuntas y marginales.

Los datos en la Tabla 2.1 podemos resumirlos tanto en forma tabular, en una tabla de frecuencias conjunta, como en forma gráfica a través, por ejemplo, de un diagrama de dispersión (Sección 2.3).

Vamos a definir una serie de términos para construir la tabla de frecuencias conjuntas:

$n_{ij}$: es el número de veces que se repite el par $(x_i,y_j)$
$n_{i \bullet}$: es el número de veces que se repite el valor $x_i$
$n_{\bullet j}$: es el número de veces que se repite el valor $y_j$
$f_{ij}$ : es el tanto por uno de veces que se repite el par $(x_i,y_j)$
$f_{i \bullet}$: es el tanto por uno de veces que se repite el valor $x_i$
$f_{\bullet j}$: es el tanto por uno de veces que se repite el valor $y_j$

La tabla de frecuencias absolutas conjuntas (Tabla 2.2) se construye introduciendo por filas los valores que toma una variable (generalmente la variable X) y por columnas los que toma la otra variable (variable Y). A continuación, cada celda de la tabla represente el número de veces que se repite cada par de valores ($x_i,y_j$), es decir, $n_{ij}$

Tabla 2.2: Tabla de frecuencias absolutas conjuntas.

X`\`Y	$y_1$	$y_2$	$\cdots$	$y_j$	$\cdots$	$y_J$
$x_1$	$n_{11}$	$n_{12}$	$\cdots$	$n_{1j}$	$\cdots$	$n_{1J}$
$x_2$	$n_{21}$	$n_{22}$	$\cdots$	$n_{2j}$	$\cdots$	$n_{2J}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$x_i$	$n_{i1}$	$n_{i2}$	$\cdots$	$n_{ij}$	$\cdots$	$n_{iJ}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$x_I$	$n_{I1}$	$n_{I2}$	$\cdots$	$n_{Ij}$	$\cdots$	$n_{IJ}$

Si las variables son cuantitativas la tabla de frecuencias conjunta también se denomina tabla de doble entrada, tabla cruzada o tabla de correlación.

Sin embargo, cuando las variables son cualitativas, la tabla de frecuencias conjuntas suele referirse como tabla de contingencia.

Las tablas cruzadas o de doble entrada se construyen para resumir la información y tener una idea de cómo se distribuyen las variables. Las medidas estadísticas se obtienen siempre a partir de los datos brutos.

Ejemplo 2.1 Obtén la distribución de frecuencias absolutas conjuntas a partir de los datos brutos que se recogen en la Tabla 2.1.

Solución: Ordenamos por filas, de menor a mayor, los distintos valores ($x_1=1,\text{ }x_2=3,\text{ }x_3=4$) que toma la variable X (Experiencia), y por columnas los que toma la variable Y (Salario): $y_1=1,200,\text{ }y_2=1,300,\text{ }y_3=1,400$.

A continuación, contamos el número de veces que se repite el par ($x_1=2,y_1=1,200$) en nuestro conjunto de datos (Tabla 2.1). Vemos que el par ($x_1=2,y_1=1,200$) se repite 4 veces ($n_{11}=4$). El par ($x_1=2,y_2=1,300$) se repite $n_{12}=1$ y así sucesivamente. La tabla cruzada de frecuencias conjuntas quedaría:

Tabla 2.3: Tabla de frecuencias absolutas conjuntas del ejemplo 2.1.

X`\`Y	$y_1=1,200$	$y_2=1,300$	$y_3=1,400$
$x_1=2$	$n_{11}=4$	$n_{12}=1$	$n_{13}=0$
$x_2=3$	$n_{21}=1$	$n_{22}=3$	$n_{23}=0$
$x_3=4$	$n_{31}=0$	$n_{32}=1$	$n_{33}=5$

Interpretamos algunos resultados:

$n_{22}= 3$: tres empleados tienen una experiencia de 3 años ($x_2=3$) y un salario de 1,300 euros ($y_2=1,300$).
$n_{13}=0$: ningún empleado de los seleccionados tiene una experiencia de 1 año y un salario de 1,400 euros.
$n_{32}=1$: un empleado tiene 4 años de experiencia y un salario de 1,300 euros.

A la Tabla 2.2 se le puede añadir la columna $n_{i\bullet}$ para contar el número de veces que se repite cada valor $x_i$, y la fila $n_{\bullet j}$ para contar el número de veces que se repite cada valor $y_j$. Esto se muestra en la Tabla 2.4.

Tabla 2.4: Tabla de frecuencias absolutas conjuntas y marginales.

X`\`Y	$y_1$	$y_2$	$\cdots$	$y_j$	$\cdots$	$y_J$	$n_{i\bullet}$
$x_1$	$n_{11}$	$n_{12}$	$\cdots$	$n_{1j}$	$\cdots$	$n_{1J}$	$n_{1\bullet}$
$x_2$	$n_{21}$	$n_{22}$	$\cdots$	$n_{2j}$	$\cdots$	$n_{2J}$	$n_{2\bullet}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$x_i$	$n_{i1}$	$n_{i2}$	$\cdots$	$n_{ij}$	$\cdots$	$n_{iJ}$	$n_{i\bullet}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$x_I$	$n_{I1}$	$n_{I2}$	$\cdots$	$n_{Ij}$	$\cdots$	$n_{IJ}$	$n_{I\bullet}$
$n_{\bullet j}$	$n_{\bullet1}$	$n_{\bullet2}$	$\cdots$	$n_{\bullet j}$	$\cdots$	$n_{\bullet J}$	$n$

De esta forma, en una misma tabla de frecuencias tendríamos:

la distribución de frecuencias conjuntas de la variable bidimensional (X,Y): $(x_i,y_j,n_{ij})$
la distribución marginal de la variable X: $(x_i,n_{i\bullet})$
la distribución marginal de la variable Y: $(y_j,n_{\bullet j})$

Observemos que en la tabla de doble entrada de frecuencias absolutas (Tabla 2.4) se cumple:\[ \displaystyle\sum_{i=1}^In_{i\bullet}=\sum_{j=1}^Jn_{\bullet j}=\sum_{i=1}^I\sum_{j=1}^Jn_{ij}=n \tag{2.1}\]

Ejemplo 2.2 Añade las frecuencias marginales de experiencia (variable X) y salario (variable Y) a la tabla cruzada obtenida en el Ejemplo 2.1.

Solución: Sumando por filas las frecuencias conjuntas obtendremos las frecuencias absolutas marginales de la variable X.\[ \displaystyle n_{i\bullet}=\sum_{j=1}^Jn_{ij} \tag{2.2}\] Por ejemplo: \[(i=1)\hspace{5mm}n_{1\bullet}=\displaystyle \sum_{j=1}^{J=3}n_{1j}=n_{11}+n_{12}+n_{13}=4+1+0=5\] Sumando por columnas las frecuencias conjuntas obtendremos las frecuencias absolutas marginales de la variable Y.\[\displaystyle n_{\bullet j}=\sum_{i=1}^In_{ij} \tag{2.3}\] Análogamente, para $j=2$, por ejemplo, tendríamos: \[(j=2)\hspace{5mm}n_{\bullet2}=\displaystyle \sum_{i=1}^{I=3}n_{i2}=n_{12}+n_{22}+n_{32}=1+3+1=5\] Por tanto, la tabla de frecuencias absolutas conjunta y marginales queda:

Tabla 2.5: Tabla de frecuencias conjuntas y marginales del ejemplo 2.2.

X`\`Y	$y_1=1,200$	$y_2=1,300$	$y_3=1,400$	$n_{i\bullet}$
$x_1=2$	$n_{11}=4$	$n_{12}=1$	$n_{13}=0$	$n_{1\bullet}=5$
$x_2=3$	$n_{21}=1$	$n_{22}=3$	$n_{23}=0$	$n_{2\bullet}=4$
$x_3=4$	$n_{31}=0$	$n_{32}=1$	$n_{33}=5$	$n_{3\bullet}=6$
$n_{\bullet j}$	$n_{\bullet1}=5$	$n_{\bullet2}=5$	$n_{\bullet3}=5$	$n=15$

Ahora, podemos ver en la Tabla 2.5 que $n_{2\bullet}=4$, es decir, hay 4 empleados que tienen una experiencia de 3 años (no nos importa en este caso sus salarios). También que $n_{\bullet3}=5$, lo que significa que 5 empleados tienen un salario de 1,400 euros (no estamos interesados en sus años de experiencia).

También podemos verificar la relación entre las frecuencias conjutas y marginales dada en Ecuación 2.1:

la suma de las frecuencias absolutas marginales de la variable X es igual al número de observaciones $n$.\[\displaystyle\sum_{i=1}^{I=3}n_{i\bullet}=n_{1\bullet}+n_{2\bullet}+n_{3\bullet}=5+4+6=15\]
la suma de las frecuencias absolutas marginales de la variable Y es igual al número de observaciones $n$. \[\displaystyle\sum_{j=1}^{J=3}n_{\bullet j}=n_{\bullet 1}+n_{\bullet 2}+n_{\bullet 3}=5+5+5=15\]
la suma de las frecuencias absolutas conjuntas es igual al número de observaciones $n$. \[\displaystyle\sum_{i=1}^{I=3}\sum_{j=1}^{J=3}n_{ij}=\] \[=n_{11}+n_{12}+n_{13}+n_{21}+n_{22}+n_{23}+n_{31}+n_{32}+n_{33}=\] \[=4+1+0+1+3+0+0+1+5=15\]

Ejemplo 2.2. con Excel. Podemos construir tablas de frecuencias conjuntas con las tablas dinámicas de Excel.

Abrimos un nuevo libro de Excel y copiamos los datos de la Tabla 2.1 comenzando en la columna A.

Guardad el archivo con el nombre datos_tema_2.xlsx, lo utilizaremos en posteriores ejemplos.

Nos situamos en la celda E1 e insertamos una tabla dinámica. Seleccionamos como rango de datos el rango de columnas A:C y dejamos la opción de insertar la tabla en la celda E1. Pulsamos Aceptar para crear la tabla. Inmediatamente se crea la plantilla de configuración de campos de la tabla dinámica, como se muestra en la Figura 2.1.

Figura 2.1: Tabla dinámcia, plantilla incial.

Observamos que en la caja correspondiente a la selección de campos se listan los tres encabezados de nuestra tabla de datos.

Arrastramos el campo Experiencia a filas y el campo Salario a columnas. A valores vamos a arrastrar Experiencia (es indistinto si arrastramos Salarios); pero no queremos que sume los años de experiencia, la opción por defecto, sino que cuente los trabajadores con los distinos años de experiencia. Para ello, hacemos clic en Suma de Experiencia > Configuración de campo de valor… > Recuento. Ya tenemos nuestra tabla de doble entrada con las frecuencias absolutas conjuntas y las marginales (Figura 2.1), que aparecen con la etiqueta Total general. Cambiamos la etiqueta de fila por Experiencia y la etiqueta de columna por Salario.

Observad el botón de desplegable que se encuentra junto a las etiquetas. Este botón nos permitirá seleccionar o filtrar valores de las variables, muy interesante para obtener distribuciones condicionadas (ver Sección 2.2.2). Ahora lo vamos a usar para eliminar la fila en blanco que se ha añadido en la tabla dinámica. Hacemos clic sobre el botón de la etiqueta Experiencia, quitamos la selección (en blanco) y pulsamos Aceptar. Se ha eliminado la fila en blanco de la tabla. Fijaros que ha cambiado la apariencia del botón, ahora es y nos indica que se ha realizado un filtrado o selección.

Figura 2.2: Tabla dinámica. Frecuencias conjuntas conjuntas y marginales.

Guardad el libro Excel con el nombre ej_2_2.

Puedes seguir cómo realizar una tabla dinámica para obtener la tabla de frecuencias conjuntas en [https://www.uv.es/ticstat/tabla_ej2_2.gif](https://www.uv.es/ticstat/tabla_ej2_2.gif)

Partiendo de la tabla de frecuencias absolutas conjuntas y marginales (Tabla 2.4), si dividimos por el número de total de observaciones ($n$) obtendremos la distribución de frecuencias relativas, tanto conjuntas como marginales (Tabla 2.6).

Tabla 2.6: Tabla de frecuencias relativas conjuntas y marginales.

X`\`Y	$y_1$	$y_2$	$\cdots$	$y_j$	$\cdots$	$y_J$	`\|`	$f_{i\bullet}$
$x_1$	$f_{11}$	$f_{12}$	$\cdots$	$f_{1j}$	$\cdots$	$f_{1J}$	`\|`	$f_{1\bullet}$
$x_2$	$f_{21}$	$f_{22}$	$\cdots$	$f_{2j}$	$\cdots$	$f_{2J}$	`\|`	$f_{2\bullet}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	`\|`	$\vdots$
$x_i$	$f_{i1}$	$f_{i2}$	$\cdots$	$f_{ij}$	$\cdots$	$f_{iJ}$	`\|`	$f_{i\bullet}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	`\|`	$\vdots$
$x_I$	$f_{I1}$	$n_{I2}$	$\cdots$	$f_{Ij}$	$\cdots$	$f_{IJ}$	`\|`	$f_{I\bullet}$
—	—	—	—	—	—	—	—	—
$f_{\bullet j}$	$f_{\bullet1}$	$f_{\bullet2}$	$\cdots$	$f_{\bullet j}$	$\cdots$	$f_{\bullet J}$	`\|`	$1$

Observemos, a partir la tabla cruzada de frecuencias relativas (Tabla 2.6), que se cumple la siguiente relación:\[ \displaystyle\sum_{i=1}^If_{i\bullet}=\sum_{j=1}^Jf_{\bullet j}=\sum_{i=1}^I\sum_{j=1}^Jf_{ij}=1 \tag{2.4}\]

Ejemplo 2.3 A partir de la tabla cruzada obtenida en el Ejemplo 2.2, construye la tabla de frecuencias relativas conjuntas y marginales.

Solución: Divididendo por $n=15$ (número total de observaciones) la Tabla 2.5 se obtiene la tabla cruzada de frecuencias relativas. El resultado se muestra en la Tabla 2.7.

Tabla 2.7: Tabla de frecuencias relativas conjuntas y marginales del Ejemplo 2.3.

X`\`Y	$y_1=1,200$	$y_2=1,300$	$y_3=1,400$	`\|`	$f_{i\bullet}$
$x_1=2$	$f_{11}=4/15$	$f_{12}=1/15$	$f_{13}=0$	`\|`	$f_{1\bullet}=5/15$
$x_2=3$	$f_{21}=1/15$	$f_{22}=3/15$	$f_{23}=0$	`\|`	$f_{2\bullet}=4/15$
$x_3=4$	$f_{31}=0$	$f_{32}=1/15$	$f_{33}=5/15$	`\|`	$f_{3\bullet}=6/15$
—	—	—	—	—	—
$f_{\bullet j}$	$f_{\bullet1}=5/15$	$f_{\bullet2}=5/15$	$f_{\bullet3}=5/15$	`\|`	$1$

Verificamos que se cumple la relación dada en Ecuación 2.4:

la suma de las frecuencias relativas marginales de la variable X es igual a 1.
\[\displaystyle\sum_{i=1}^{I=3}f_{i\bullet}=f_{1\bullet}+f_{2\bullet}+f_{3\bullet}=5/15+4/15+6/15=1\]
la suma de las frecuencias relativas marginales de la variable Y es igual a 1.
\[\displaystyle\sum_{j=1}^{J=3}f_{\bullet j}=f_{\bullet 1}+f_{\bullet 2}+f_{\bullet 3}=5/15+5/15+5/15=1\]
la suma de las frecuencias relativas conjuntas es igual a 1. \[\displaystyle\sum_{i=1}^{I=3}\sum_{j=1}^{J=3}f_{ij}=\] \[=f_{11}+f_{12}+f_{13}+f_{21}+f_{22}+f_{23}+f_{31}+f_{32}+f_{33}=\] \[=4/15+1/15+0+1/15+3/15+0+0+1/15+5/15=1\]

Ejemplo 2.3. con Excel. Una vez tenemos nuestra tabla dinámica, que representa la distribución de frecuencias absolutas conjuntas y marginales, obtener la tabla en términos relativos es sencillo.

Abrimos el archivo Excel ej_2_2.xlsx. Hacemos clic en cualquier parte de la tabla dinámica para mostrar la lista de campos.

Si al clicar sobre la tabla no aparece la lista de campos, haced clic en el botón derecho del ratón y seleccionar la última opción: Mostrar lista de campos.

Figura 2.3: Configuración de campo de valor: Opciones de Mostrar valor.

Con la lista de campos abierta, clicamos en Cuenta de Experiencia > Configuración de campo de valor…. La ventana que se abre muestra por defecto las opciones de la pestaña Resumir valor por; seleccionamos la pestaña Mostrar valores como y desplegamos las opciones, como se muestra en la Figura 2.3. La opción por defecto es Sin cálculo, otras opciones son:

% del total general.
% del total de columnas.
% del total de filas.
etc.

Recordemos que las frecuencias relativas las calculamos respecto del tamaño de la muestra, que es el total de observaciones; por tanto, seleccionamos la opción: % del total general. La tabla de frecuencias relativas conjuntas y marginales quedará como se reproduce en la Figura 2.4.

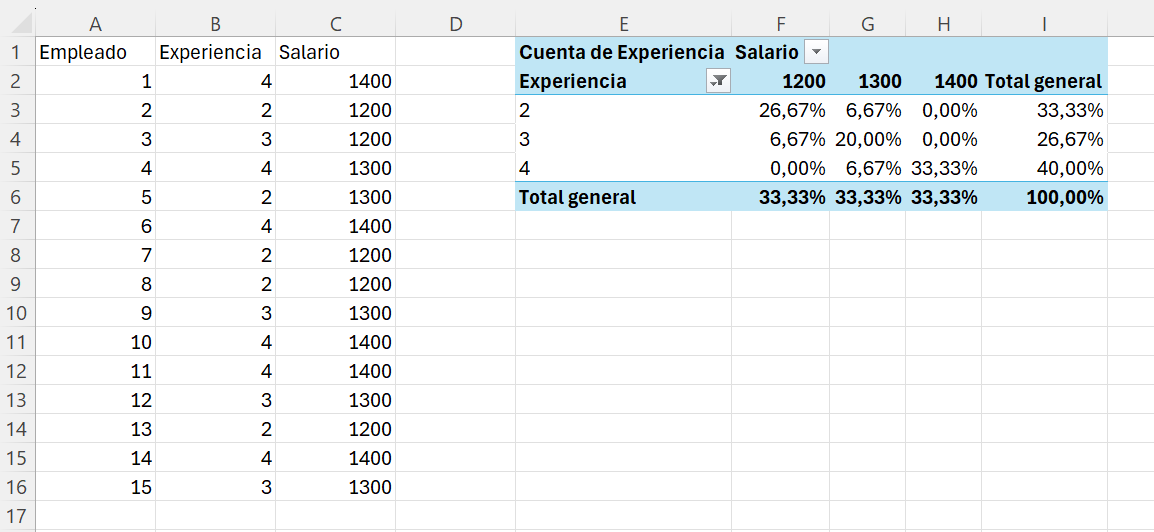
Figura 2.4: Tabla dinámica. Frecuencias relativas conjuntas y marginales.

Guardad el libro Excel con el nombre ej_2_3.

Puedes seguir cómo realizar una tabla dinámica para obtener la tabla de frecuencias relativas en [https://www.uv.es/ticstat/tabla_ej2_3.gif](https://www.uv.es/ticstat/tabla_ej2_3.gif)

Ejemplo 2.4 De una variable bidimensional (X,Y) se ha obtenido la siguiente tabla de frecuencias absolutas conjuntas y marginales:

Tabla 2.8: Tabla cruzada incompleta del Ejemplo 2.4.

X`\`Y	1,000	1,300	1,600	1,900	`\|`	$n_{i\bullet}$
[0,10[	–	3	2	–	`\|`	10
[10,20[	10	–	5	5	`\|`	30
[20,30[	5	10	–	2	`\|`	–
[30,40[	–	7	–	1	`\|`	14
[40,50]	1	2	8	–	`\|`	21
—	—	—	—	—	—	—
$n_{\bullet j}$	20	–	27	21	`\|`	–

Completa la tabla de frecuencias.

Solución: Para resolver este ejercicio debemos tener en cuenta las relaciones reflejadas en la Ecuación 2.1 y la Ecuación 2.4.

Tabla 2.9: Tabla cruzada completada del Ejemplo 2.4.

X`\`Y	1,000	1,300	1,600	1,900	`\|`	$n_{i\bullet}$
[0,10[	2	3	2	3	`\|`	10
[10,20[	10	10	5	5	`\|`	30
[20,30[	5	10	8	2	`\|`	25
[30,40[	2	7	4	1	`\|`	14
[40,50]	1	2	8	10	`\|`	21
—	—	—	—	—	—	—
$n_{\bullet j}$	20	32	27	21	`\|`	100

2.2.2 Distribuciones de frecuencias condicionadas

Cuando trabajamos con dos o más variables en muchas ocasiones resulta de interés obtener determinadas medidas (media, mediana, etc.) de una de ellas condicionada a que otra (u otras) toman ciertos valores.

Las distribuciones de frecuencias condicionadas son distribuciones de frecuencias unidimensionales y, por tanto, es de aplicación todo lo visto en el capítulo 1.

Una distribución de frecuencias, absolutas o relativas, condicionada es un resumen tabular de la distribución de frecuencias de una variable condicionada a que la otra variable toma cierto valor. Si nos centramos en el estudio de dos variables (X,Y), podemos hablar de:

La distribución de frecuencias absolutas y relativas de X condicionada a que Y toma un determinado valor: distribución de $X/Y=y_j$

Tabla 2.10: Tabla de frecuencias absolutas y relativas de X condicionada al valor $Y=y_j$.

$X/Y=y_j$	$n_{ij}$	$f_{ij}$
$x_1$	$n_{1j}$	$f_{1j}=\frac{n_{1j}}{n_{\bullet j}}$
$x_2$	$n_{2j}$	$f_{2j}=\frac{n_{2j}}{n_{\bullet j}}$
$\vdots$	$\vdots$	$\vdots$
$x_i$	$n_{ij}$	$f_{ij}=\frac{n_{ij}}{n_{\bullet j}}$
$\vdots$	$\vdots$	$\vdots$
$x_I$	$n_{Ij}$	$f_{Ij}=\frac{n_{Ij}}{n_{\bullet j}}$
	—	—
	$n_{\bullet j}$	$1$

Ejemplo 2.5 A partir de la tabla cruzada del Ejemplo 2.2, obtener la distribución de frecuencias absolutas de X (Experiencia) condicionada a que Y (Salario) toma el valor 1,300 ($y_2=1,300$).

Solución: Con un salario de 1,300 ($Y_2=1,300$) euros tenemos un total de 5 trabajadores ($n_{\bullet2}=5$), pero estos trabajadores no tienen la misma experiencia. Hay 1 trabajador con 2 años de experiencia, 3 con 3 años y otro con 4 años. Este resumen se refleja en la tabla de frecuencias condicionada:

Tabla 2.11: Tabla de frecuencias de X condicionadas a $Y=1,300$.

$X/Y=y_{j=2}=1,300$	$n_{i2}$
$x_1=2$	$n_{12}=1$
$x_2=3$	$n_{22}=3$
$x_3=4$	$n_{32}=1$
	—
	$n_{\bullet2}=5$

Ejemplo 2.5. con Excel. Abrimos el archivo ej_2_2.xlsx. En nuestra tabla dinámica, para obtener la distribución de frecuencias absolutas de X (Experiencia) condicionada a que Y (Salario) toma el valor 1,300 ($y_2=1,300$), vamos a desplegar los valores que toma Salario y seleccionamos (o filtramos por) el valor 1,300. El resultado será el que se muestra en la Figura 2.5.

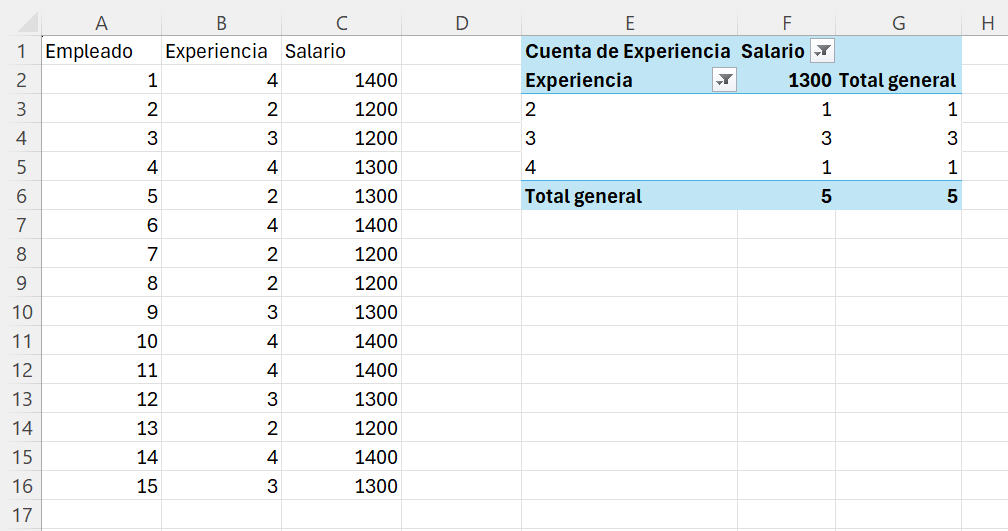
Figura 2.5: Tabla dinámica. Frecuencias conjuntas X/Y=y0.

Guardad el libro Excel con el nombre ej_2_5.

Puedes seguir cómo realizar una tabla dinámica para obtener la tabla de frecuencias absolutas de X condicionada a un valor de Y en [https://www.uv.es/ticstat/tabla_ej2_5.gif](https://www.uv.es/ticstat/tabla_ej2_5.gif)

La distribución de frecuencias absolutas y relativas de Y condicionada a que X toma un determinado valor: distribución de $Y/X=x_i$

Tabla 2.12: Tabla de frecuencias absolutas y relativas de Y condicionada al valor $X=x_i$.

$Y/X=x_i$	$n_{ij}$	$f_{ij}$
$y_1$	$n_{i1}$	$f_{i1}=\frac{n_{i1}}{n_{i\bullet}}$
$y_2$	$n_{i2}$	$f_{i2}=\frac{n_{i2}}{n_{i\bullet}}$
$\vdots$	$\vdots$	$\vdots$
$y_j$	$n_{ij}$	$f_{ij}=\frac{n_{ij}}{n_{i\bullet}}$
$\vdots$	$\vdots$	$\vdots$
$y_J$	$n_{iJ}$	$f_{iJ}=\frac{n_{iJ}}{n_{i\bullet}}$
	—	—
	$n_{i\bullet}$	$1$

Ejemplo 2.6 A partir de la tabla cruzada del Ejemplo 2.2, obtén la distribución de frecuencias absolutas de Y (Salario) condicionada a que X (Experiencia) toma el valor 4 ($X=x_3=4$).

Solución: En este caso, estamos interesados en obtener la distribución de frecuencias del Salario (variable $Y$, que toma los valores $y_1=1,200,y_2=1,300,y_3=1,400$) pero únicamente de aquellos empleados que tienen una experiencia de 4 años ($x_3=4$). Por tanto, la distribución condicionada será:

Tabla 2.13: Tabla de frecuencias de Y condicionadas a $X=4$.

$Y/X_{i=3}=4$	$n_{3j}$
$y_1=1,200$	$n_{31}=0$
$y_2=1,300$	$n_{32}=1$
$y_3=1,400$	$n_{33}=5$
	—
	$n_{3\bullet}=6$

Con 4 años de experiencia no hay ningún trabajador con un salario de 1,200 euros, uno tiene un salario de 1,300 euros y un total de 5 perciben 1,400 euros. En total, de la muestra de 15 trabajadores 6 tienen una experiencia de 4 años.

Ejemplo 2.6. con Excel. Abrimos el archivo ej_2_5.xlsx. En nuestra tabla dinámica, para obtener la distribución de frecuencias absolutas de Y (Salario) condicionada a que X (Experiencia) toma el valor 4 ($X=x_3=4$), desplegamos los valores que toma Salario y seleccionamos (o filtramos por) todos los valores, a excepción de blanco. Seguidamente, seleccionamos de los valores de experiencia únicamente el valor 4. El resultado será el que se muestra en la Figura 2.6.

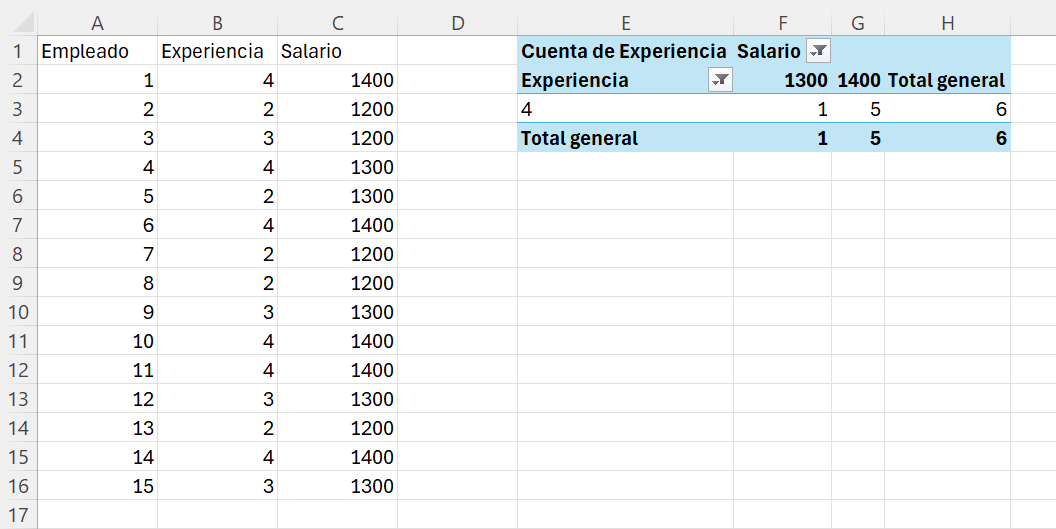
Figura 2.6: Tabla dinámica. Frecuencias conjuntas Y/X=x0.

Guardad el libro Excel con el nombre ej_2_6.

Puedes seguir cómo realizar una tabla dinámica para obtener la tabla de frecuencias absolutas de X condicionada a un valor de Y en [https://www.uv.es/ticstat/tabla_ej2_6.gif](https://www.uv.es/ticstat/tabla_ej2_6.gif)

En las tablas dinámicas, si en lugar de celdas en blanco cuando no hay valores queremos que aparecezca 0, tenemos que hacer clic en cualquier lugar de la tabla y después botón derecho del ratón. Seleccionar Opciones de tabla dinámica… > Diseño y formato, en la caja correspondiente a Para celdas vacías, mostrar: escribir 0.

2.3 Diagrama de dispersión.

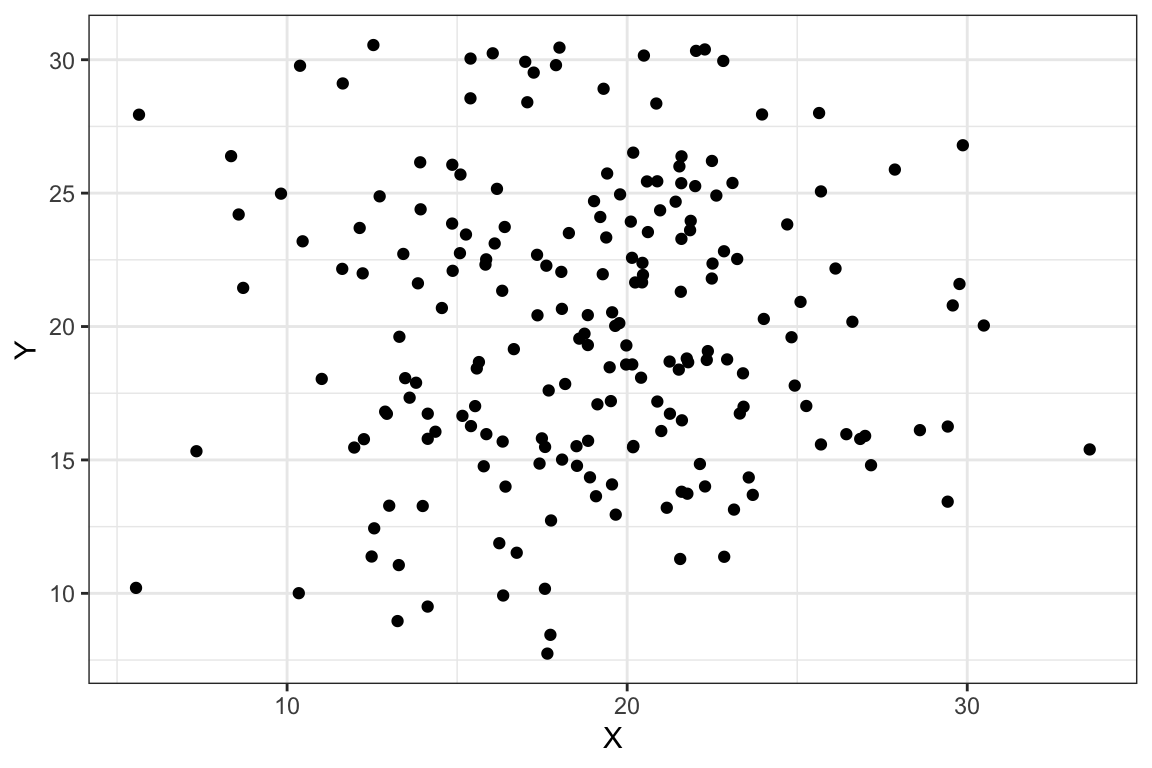
Un diagrama de dispersión es un gráfico en el que se representan los pares de puntos ($x_i,y_i)$. Generalmente, en el eje de abcisas se representan los valores de la variable que puede tener cierto efecto sobre la otra variable considerada, que se representa en el eje de ordenadas. El análisis de la nube de puntos obtenida permite tener una primera idea acerca de la posible relación entre las variables. Consideremos el diagrama de dispersión que se muestra en la Figura 2.7. Si observamos esta nube de puntos, no parece que las variables X e Y estén relacionadas de ninguna manera. La nube de puntos no muestra un patrón, los puntos se distribuyen en el plano de forma aleatoria, lo que sugiere que las variables consideradas no muestran ningún tipo de relación entre ellas.

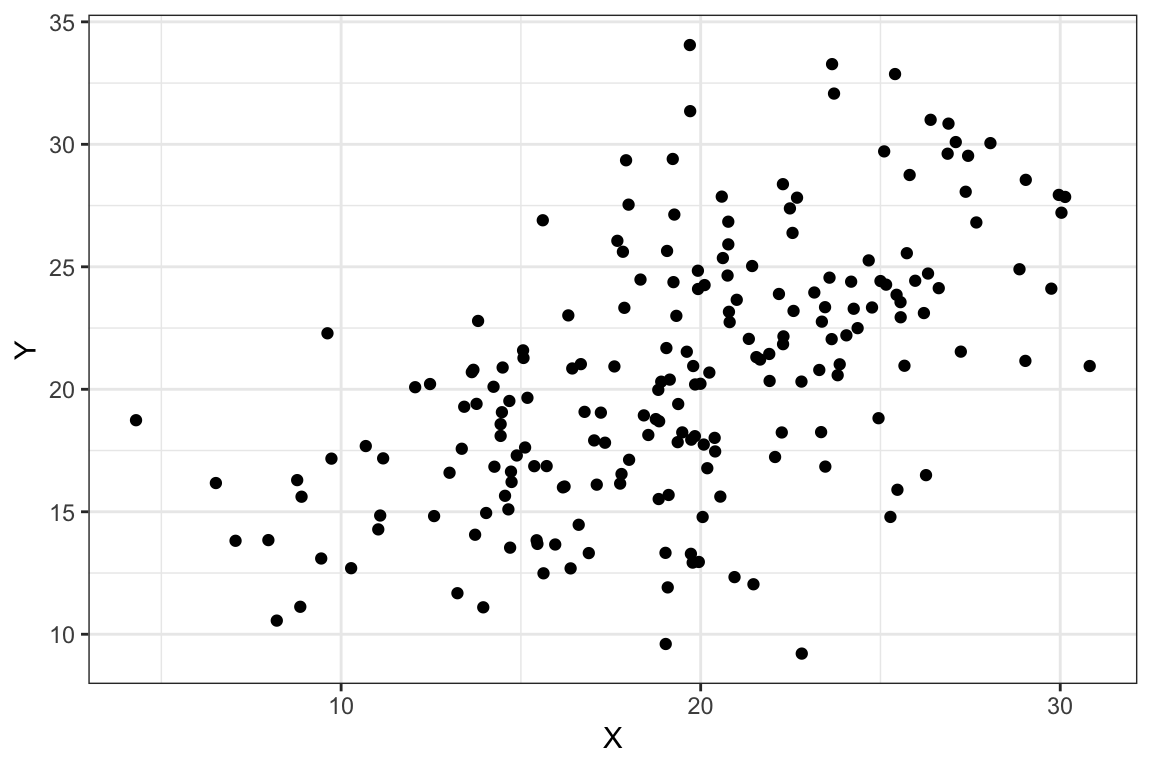
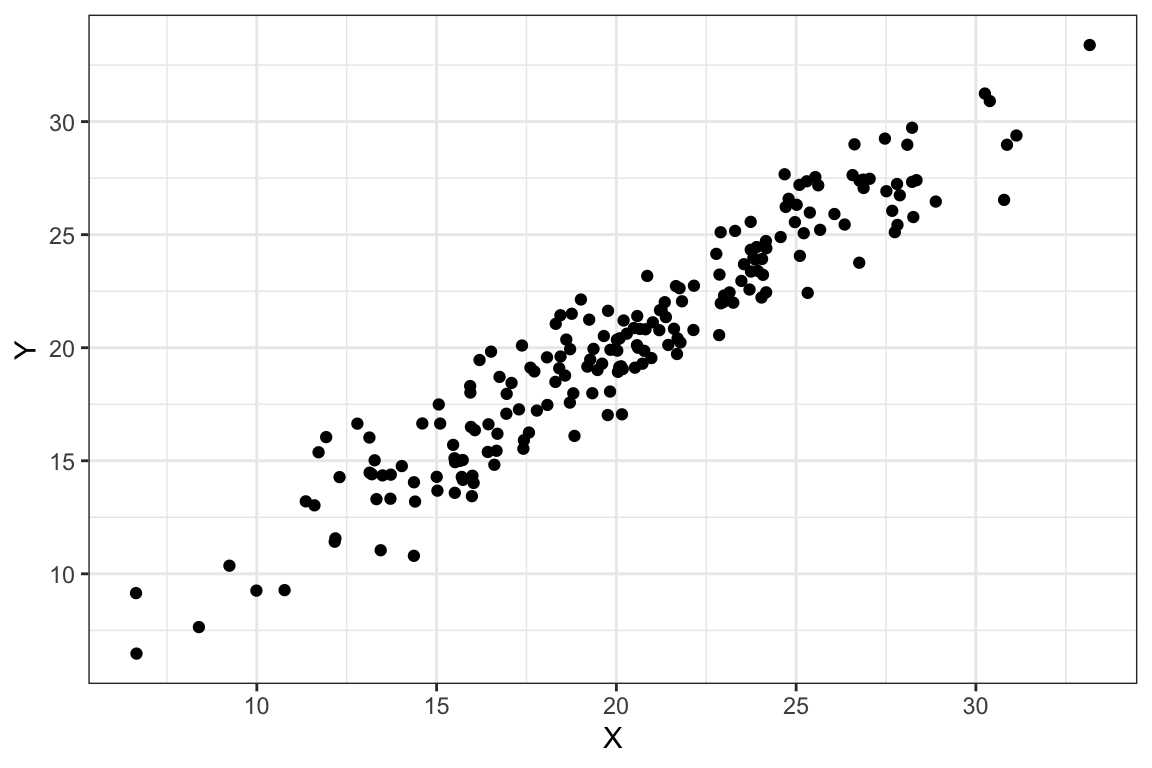
Figura 2.7: Diagrama de dispersión, nube de puntos sin patrón.

Sin embargo, consideremos ahora los gráficos de dispersión que se muestran en la Figura 2.8. En los dos diagramas etiquetados como Figura a y b, se observa una cierta relación lineal, positiva porque la nube de puntos es ascendente y más intensa en el diagrama de la derecha (Figura b) porque la nube de puntos se ajusta mejor a una (hipotética) recta. Similarmente, en los diagramas representados en las Figuras c y d la relación lineal es negativa; la nube de puntos es descendente y más intensa en el diagrama de dispersión de la derecha (Figura d).

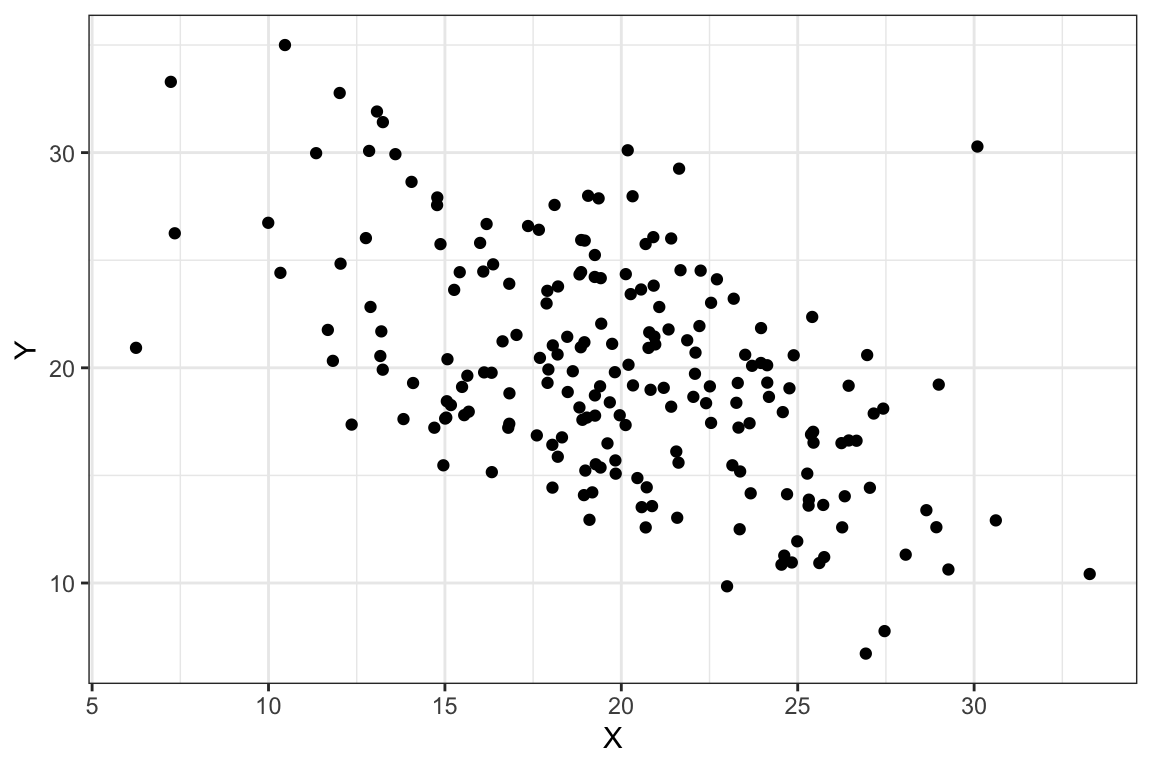
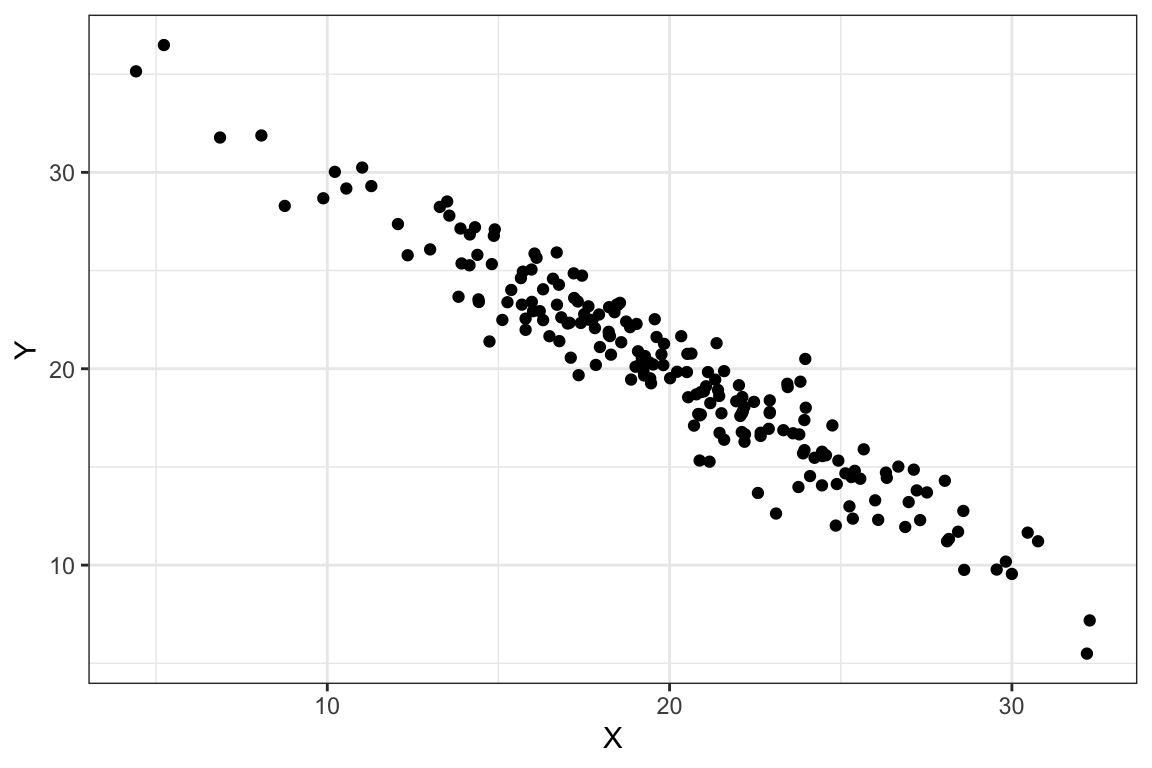
Anteriormente se ha supuesto una hipotética relación lineal entre las variables, pero la relación también puede ser no lineal, como se muestra en los siguientes dos diagramas de dispersión capturados en la Figura 2.9.

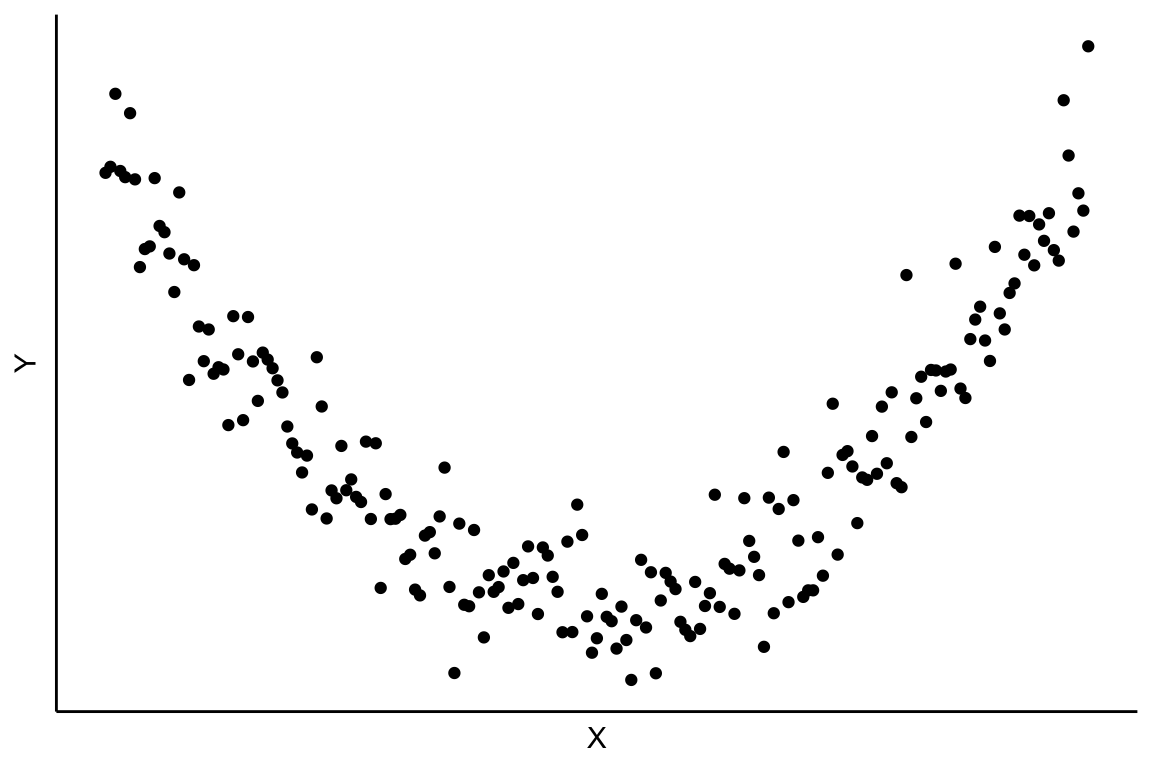
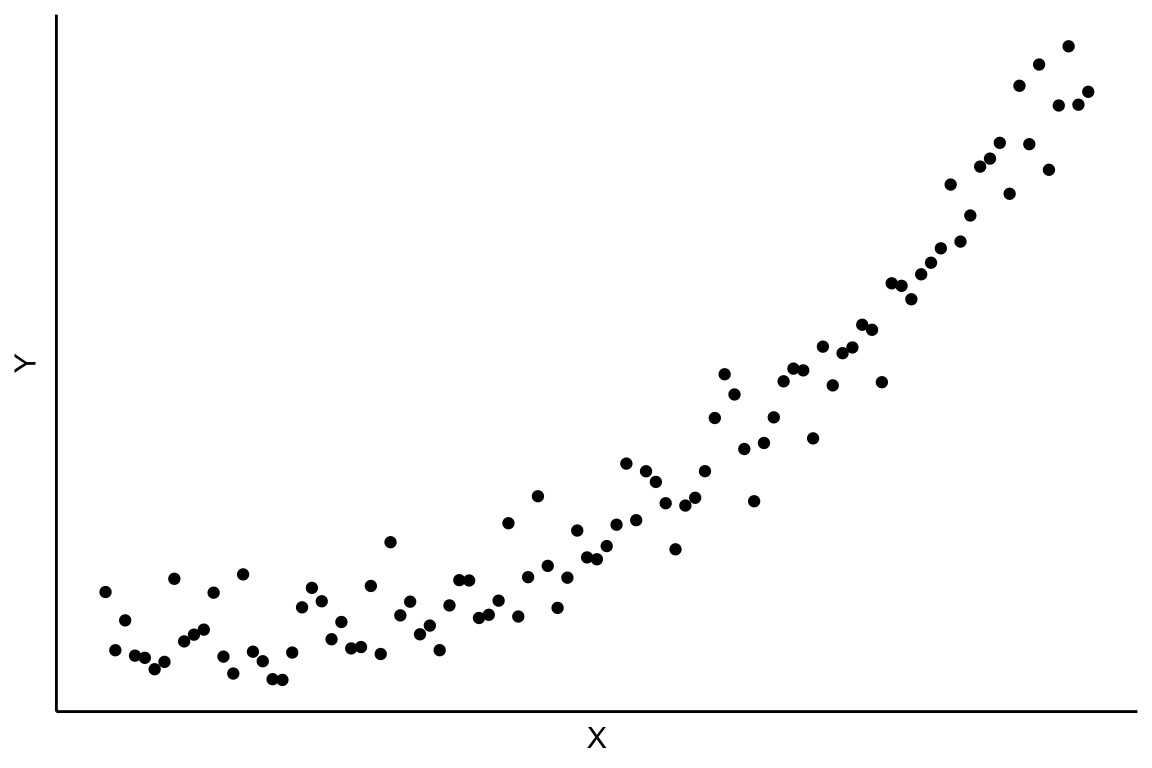
En este y el siguiente capítulo únicamente consideraremos que, si existe, la relación entre las variables X e Y es lineal.

En resumen, cuando realizamos un diagrama de dispersión tenemos que analizarlo intentando dar respuesta a tres cuestiones:

¿Observamos alguna relación funcional entre las variables X e Y?
En caso de observar una relación de tipo lineal, ¿cuál es el sentido de dicha relación? Es decir, la nube de puntos es ascendente (relación positiva = covarianza positiva) o descendente (relación negativa = covarianza negativa).
La nube de puntos se ajusta mucho a una recta (correlación alta) o se ajusta poco (correlación baja).

En general, se sitúa en el eje X la variable que tiene influencia o afecta a la otra variable, que se sitúa en el eje Y.

:::{#exm-2-7} Dibuja e interpretra el gráfico de dispersión del conjunto de datos se que recogen en la Tabla 2.1. Compara tu gráfico con el obtenido en el siguiente ejemplo. :::

Ejemplo 2.7. con Excel. Vamos a representar los pares de datos de la Tabla 2.1 en un diagrama de dispersión.

Abrimos el archivo ej_2_2.xlsx. Nos situamos en la celda E9, clicamos en Insertar > (Insertar gráfico de dispersión (X,Y) o de burbujas). Seleccionamos el primer dibujo, es un gráfico de dispersión básico. Se abre el área de gráfico. Seleccionamos los datos, es decir, el rango B2:C16. Por defecto, la primera columna será la variable que irá al eje X y la segunda columna irá al eje Y. También podemos utilizar las opciones Agregar y/o Modificar para realizar la selección del conjunto de datos. Como hemos hecho en gráficos anteriores, podemos mejorar la apariciencia del diagrama de dispersión introduciendo el título principal del gráfico y de los ejes, eliminando las líneas de cuadrícula, cambiando el color y/o forma de los puntos, ajustando los valores de los ejes, etc.

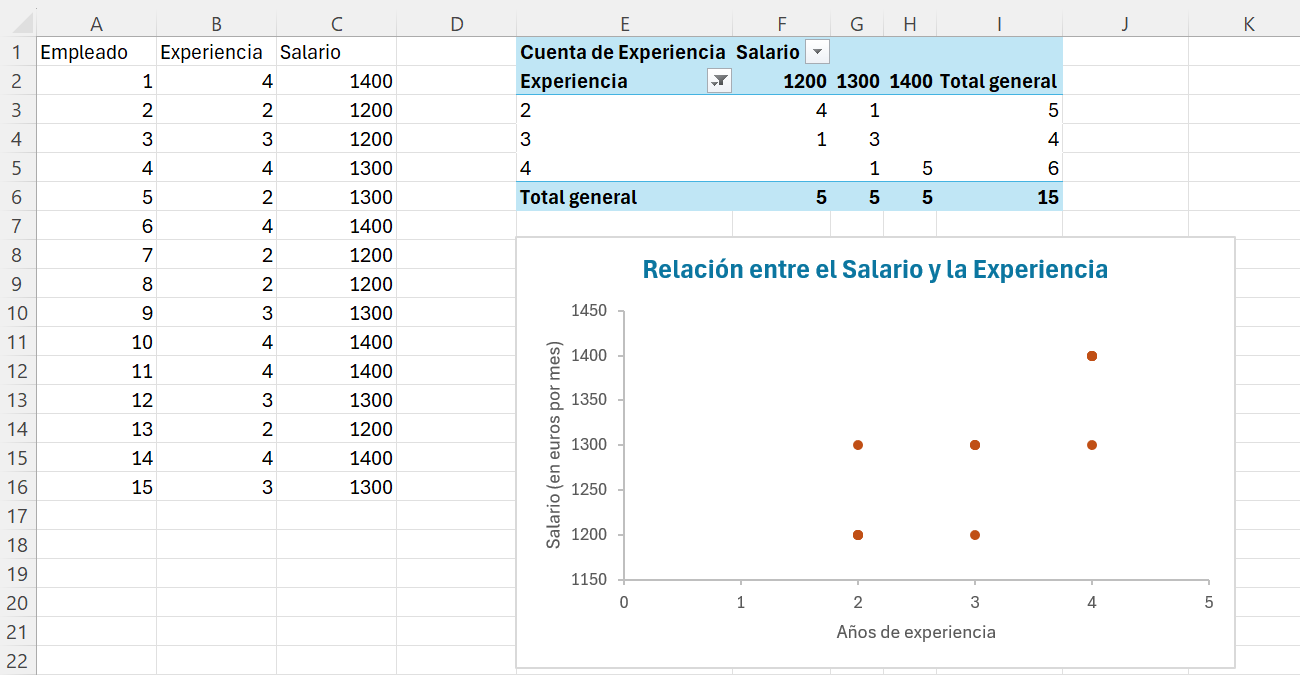
El diagrama de dispersión de nuestro conjunto de datos se muestra en la Figura 2.10.

Evidentemente, el diagrama de dispersión que hemos obtenido es muy limitado porque únicamente disponemos de 15 pares de datos, que además se repiten. Con todo, podemos intuir una nube de puntos ascendente, lo que nos hace pensar en una posible relación (lineal) positiva entre la Experiencia y el Salario. En los siguientes apartados del tema trataremos esta cuestión, la relación o asociación entre variables.

Las representaciones gráficas nos ayudan a hacernos una idea de cómo se distribuye una variable o de la posible relación entre variables, etc.; pero nuestra opinión no se tiene que basar en los gráficos, nuestras opiniones tienen que sustentarse en la interpretación de las oportunas medidas estadísticas.

Figura 2.10: Relación entre Salario y Experiencia. Diagrama de dispersión.

Guardad el libro Excel con el nombre ej_2_7.

Puedes seguir cómo realizar el diagrama de dispersión de la Figura 2.10 en la animación que encontrarás en [https://www.uv.es/ticstat/dispersion_ej_2_7.gif](https://www.uv.es/ticstat/dispersion_ej_2_7.gif)

2.3.1 Detección de valores anómalos

En el Sección 1.8 estudiamos cómo detectar observaciones anómalas en una variable. Sabemos que para detectar estos valores atípicos podemos utilizar, entre otros métodos, el criterio de los valores tipificados y la regla de Tukey (basada en el recorrido intercuartílico). Sin embargo, este primer análisis univariante debe ir acompañado de diagnósticos bidimensionales (entre pares de variables) y multivariantes (Hair, Anderson, y R. L. Tatham (2010)).

Únicamente con carácter informativo, para realizar un diagnóstico bivariante de los valores atípicos podemos recurrir a los diagramas de dispersión. En estos casos lo que hacemos es representar el diagrama de dispersión y sobre él dibujamos una elipse que representa habitualmente el 95% del intervalo de confianza de una distribución normal bivariante. El lector interesado puede consultar Coll-Serrano (2023).

2.4 Independencia estadística

Si dos variables son independientes entonces no tienen ningún tipo de relación; los valores que toma una variable no influyen en absoluto en los valores que pueda tomar la otra. En el otro extremo se encuentra la dependencia funcional entre las variables. En este caso, los valores de una variable determinarán exactamente los valores de la otra.

Realmente, en el análisis estadístico interesa el estudio de aquellos escenarios que se situán entre los extremos: independencia - dependencia funcional.

En la Figura 2.11 se ha representado los tres casos, de izquierda a derecha: (1) independencia estadística, (2) dependencia estadística y (3) dependencia funcional.

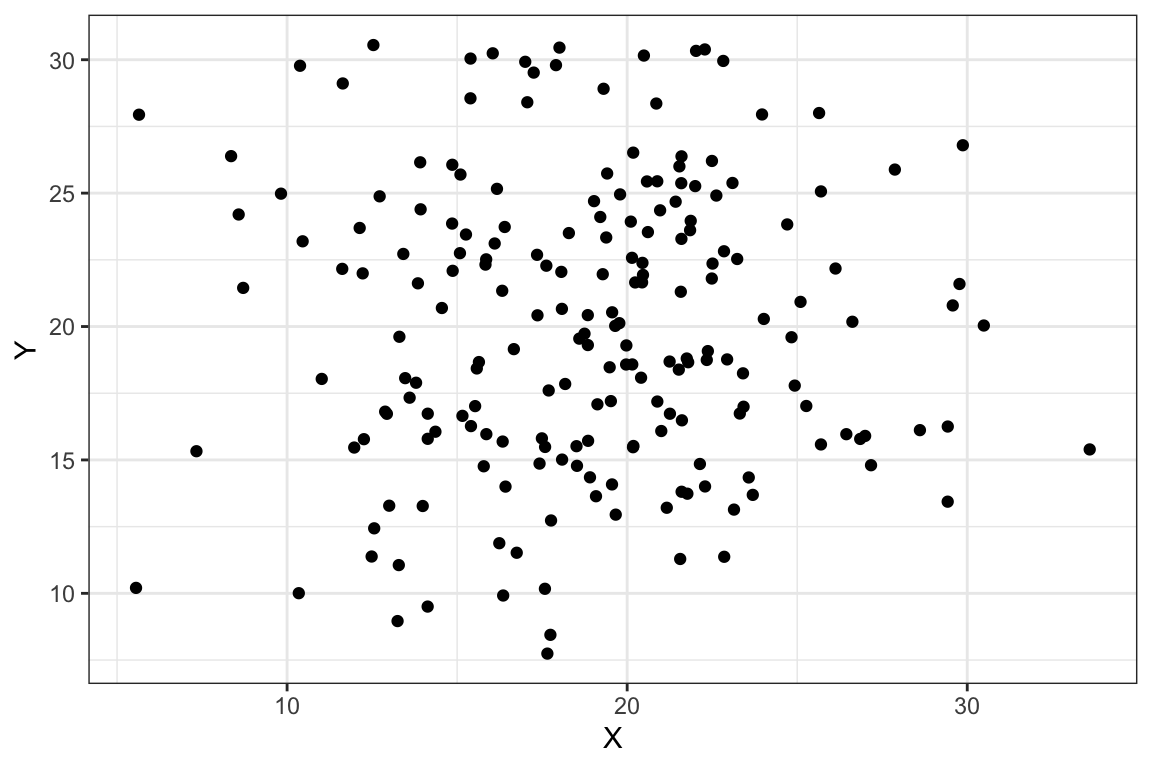
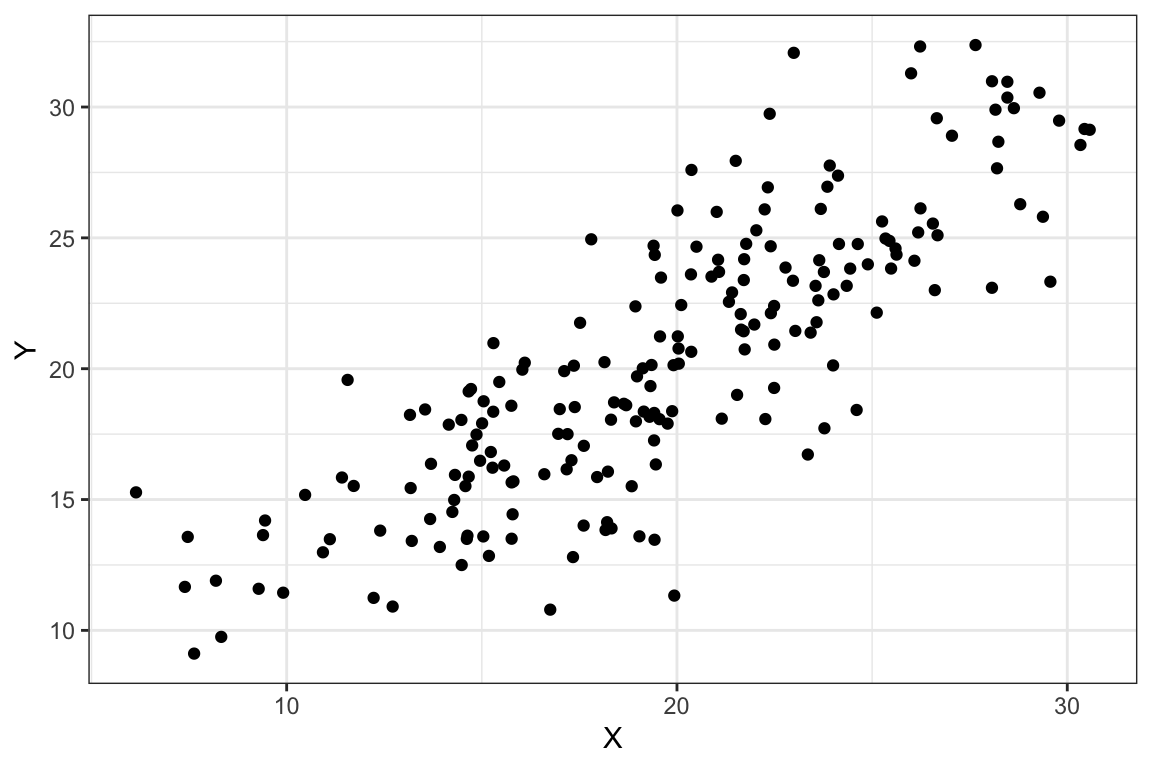
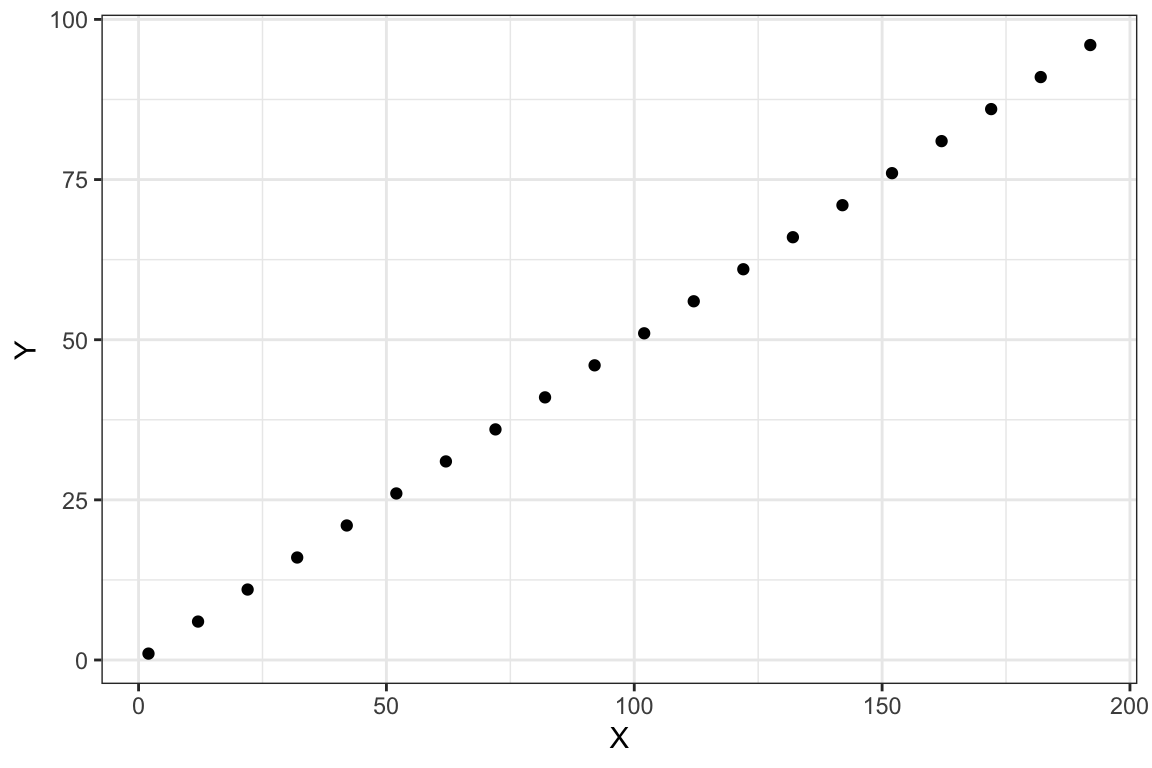
Para comprobar si dos variables X e Y son estadísticamente independientes aplicamos el conocido como teorema de caracterización. Según este teorema, las variables serán independientes si y solo si para todos los pares de valores de las variables consideradas, las frecuencias relativas conjuntas son iguales al producto de las frecuencias relativas marginales.\[ \frac{n_{ij}}{n}=\frac{n_{i\bullet}}{n} \cdot \frac{n_{\bullet j}}{n} \quad \forall i,j \tag{2.5}\]

Ejemplo 2.7 A partir de la tabla cruzada obtenida en el Ejemplo 2.2, que se reproduce más abajo, nos preguntamos: ¿son experiencia (variable X) y salario (variable Y) independientes?

Tabla 2.14: Tabla de frecuencias conjuntas y marginales del Ejemplo 2.2.

X/Y	$y_1=1,200$	$y_2=1,300$	$y_3=1,400$	`\|`	$n_{i\bullet}$
$x_1=2$	$n_{11}=4$	$n_{12}=1$	$n_{13}=0$	`\|`	$n_{1\bullet}=5$
$x_2=3$	$n_{21}=1$	$n_{22}=3$	$n_{23}=0$	`\|`	$n_{2\bullet}=4$
$x_3=4$	$n_{31}=0$	$n_{32}=1$	$n_{33}=5$	`\|`	$n_{3\bullet}=6$
—	—	—	—	—	—
$n_{\bullet j}$	$n_{\bullet1}=5$	$n_{\bullet2}=5$	$n_{\bullet3}=5$	`\|`	$n=15$

Solución: Para responder a la pregunta consideramos la Tabla 2.14 y aplicamos el teorema de caracterización (Ecuación 2.5). Comenzamos con el primer par de valores ($i=1,j=1$): \[\frac{n_{11}}{n} = \frac{n_{1\bullet}}{n} \cdot \frac{n_{\bullet 1}}{n} \longrightarrow \frac{4}{15} \neq \frac{5}{15} \cdot \frac{5}{15}\] Por tanto, como ya no puede cumplirse el teorema de caracterización para todos los pares de valores, concluimos que experiencia y salario no son estadísticamente independientes. Si se hubiese cumplido la igualdad para el par ($i=1,j=1$), deberíamos continuar con la siguiente celda ($i=1,j=2$) y así sucesivamente, hasta que para algún par $(i,j)$ no se cumpla la igualdad, lo que indicará la ausencia de independencia. Si todas las celdas verificasen la condición de independencia, entonces las variables serían estadísticamente independientes.

En la práctica la comprobación de independencia no se realiza manualmente. Cuando estudiemos los principios de la estadística inferencial aplicaremos, por ejemplo, el contraste (de hipótesis) de independencia o de incorrelación.

Cabe considerar que si dos variables son independientes entonces las distribuciones condicionadas serán iguales a las distribuciones marginales. Efectivamente, si son independientes, la variable condicionante no tendrá ninguna influencia sobre la variable condicionada.

La frecuencia relativa de $X$ condicionada a que Y toma el valor $y_j$ será:\[ f_{i/j}=\displaystyle\frac{n_{ij}}{n_{\bullet j}}= \frac{\displaystyle\frac{n_{i\bullet} \cdot n_{\bullet j}}{n}}{n_{\bullet j}} \tag{2.6}\]

Ejemplo 2.8 Consideremos la siguiente distribución bidimensional (X,Y):

Tabla 2.15: Tabla cruzada del Ejemplo 2.8.

X/Y	1	2	`\|`	$n_{i\bullet}$
0	1	2	`\|`	3
1	2	4	`\|`	6
—	—	—	—	—
$n_{\bullet j}$	3	6	`\|`	$n=9$

Obtén las distintas distribuciones condicionadas.

Solución: Si aplicásemos el teorema de caracterización (Ecuación 2.5) comprobaríamos que en este ejemplo las variables X e Y son independientes.

La distribución de frecuencias relativas de $X$ condicionada a $Y=y_1=1$ es:

Tabla 2.16: Distribución $X/Y=1$

X/Y	$f_{i/j=1}$
0	$f_{11}=\displaystyle\frac{n_{11}}{n_{\bullet1}}=\frac{1}{3}$
1	$f_{21}=\displaystyle\frac{n_{21}}{n_{\bullet1}}=\frac{2}{3}$

La distribución de frecuencias relativas de $X$ condicionada a $Y=y_2=2$ es:

Tabla 2.17: Distribución $X/Y=2$

X/Y	$f_{i/j=2}$
0	$f_{11}=\displaystyle\frac{n_{12}}{n_{\bullet2}}=\frac{2}{6}=1/3$
1	$f_{22}=\displaystyle\frac{n_{22}}{n_{\bullet2}}=\frac{4}{6}=2/3$

La distribución de frecuencias relativas de $Y$ condicionada a $X=x_1=0$ es:

Tabla 2.18: Distribución $Y/X=0$

Y/X	$f_{j/i=1}$
1	$f_{11}=\displaystyle\frac{n_{11}}{n_{1\bullet}}=\frac{1}{3}$
2	$f_{12}=\displaystyle\frac{n_{12}}{n_{1\bullet}}=\frac{2}{3}$

La distribución de frecuencias relativas de $Y$ condicionada a $X=x_2=1$ es:

Tabla 2.19: Distribución $Y/X=1$

Y/X	$f_{j/i=2}$
1	$f_{21}=\displaystyle\frac{n_{21}}{n_{2\bullet}}=\frac{2}{6}=1/3$
2	$f_{22}=\displaystyle\frac{n_{22}}{n_{2\bullet}}=\frac{4}{6}=2/3$

2.5 Covarianza.

La covarianza mide el sentido o dirección de la relación/asociación lineal entre dos variables cuantitativas y se define como la media del producto de las desviaciones de los valores de cada variable respecto de su media.

La covarianza muestral se denota por $S_{XY}$ y su expresión es:\[S_{XY}=\frac{\displaystyle\sum_{i=1}^{n}\left ( x_i - \bar{x} \right )\cdot\left ( y_i - \bar{y}\right )}{n-1} \tag{2.7}\]

La gran mayoría de los softwares estadísticos calculan la covarianza a través de la Ecuación 2.7. Sin embargo, en manuales de estadística, sobre todo de origen español, podemos ver expresada la covarianza como:\[ S_{XY}=\frac{\displaystyle\sum_{i=1}^{n}\left ( x_i - \bar{x} \right )\left ( y_i - \bar{y}\right )}{n} \tag{2.8}\] Evidentemente, cuanto mayor sea el tamaño de la muestra n menor será la diferencia entre calcular la covarianza con la Ecuación 2.7 o con la Ecuación 2.8.

Ejemplo 2.9 Las dos primeras columnas de la Tabla 2.20 recogen los datos brutos de la Experiencia (X) y Salario (Y) de una muestra de 15 empleados (nota: el resto de columnas serán calculadas durante la resolución del ejemplo). Calcula la varianza de la Experiencia, la varianza del Salario y la covarianza entre Experiencia y Salario.

Solución: Calculamos las varianzas muestrales a partir de las siguientes expresiones:

\[{S_X^2}=\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}\] \[{S_Y^2}=\frac{\displaystyle\sum_{i=1}^{n}(y_i-\bar{y})^2}{n-1}\] Para el cálculo de las varianzas (muestrales) necesitamos calcular las medias de las variables: \[\bar{x}=\frac{\displaystyle\sum_{i=1}^{n=15}x_i}{n} \hspace{1.5cm} \bar{y}=\frac{\displaystyle\sum_{i=1}^{n=15}y_i}{n}\] Los cálculos necesarios los iremos recogiendo en una tabla, Veamos cómo obtener las distintas columnas de la Tabla 2.20.

Sumando todos los valores de la columna 1 obtenemos que $\displaystyle\sum_{i=1}^{n=15}x_i=46$, y la media será: \[\bar{x}=\frac{\displaystyle\sum_{i=1}^{n=15}x_i}{n}=\frac{46}{15}=3.0667\hspace{1mm}\text{años}\]

Para calcular la media del Salario sumamos los valores de la columna 2, de forma que:

\[\bar{y}=\frac{\displaystyle\sum_{i=1}^{n=15}y_i}{n}=\frac{19,500}{15}=1,300\hspace{1mm}\text{euros}\]

Tabla 2.20: Tabla para cálculos intermedios de la covarianza.

$x_i$	$y_i$	$x_i-\bar{x}$	$y_i-\bar{y}$	$(x_i-\bar{x})^2$	$(y_i-\bar{y})^2$	$(x_i-\bar{x})(y_i-\bar{y})$
4	1,400	0.9333	100	0.871	10,000	93.33
2	1,200	-1.0667	-100	1.378	10,000	106.67
3	1,200	-0.0667	-100	0.0044	10,000	6.7
4	1,300	0.9333	0	0.871	0	0
2	1,300	-1.0667	0	1.378	0	0
4	1,400	0.9333	100	0.871	10,000	93.33
2	1,200	-1.0667	-100	1.1378	10,000	106.67
2	1,200	-1.0667	-100	1.1378	10,000	106.67
3	1,300	-0.0667	0	0.0044	0	0
4	1,400	0.9333	100	0.871	10,000	93.33
4	1,400	0.9333	100	0.871	10,000	93.33
3	1,300	-0.0667	0	0.0044	0	0
2	1,200	-1.0667	-100	1.1378	10,000	106.67
4	1,400	0.9333	100	0.871	10,000	93.33
3	1,300	-0.0667	0	0.0044	0	0
—	—				—	—
46	19,500			10.9326	100,000	900

La columna 3 en la Tabla 2.20 la obtenemos restando a la columna 1 la media de X; y la columna 4 al restar a la columna 2 la media de Y. La columna 5 se obtiene al elevar al cuadrado los valores de la columna 3, la suma de los valores de esta columna será el numerador de la varianza de X. La columna 6 se obtiene al elevar al cuadrado los valores de la columna 4, y su suma será el numerador de la varianza de Y.

Hacemos las operaciones considerando 4 decimales.

Las varianzas (muestrales) de las variables consideradas serán: \[{S_X^2}=\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}=\frac{10.9326}{15-1}=0.7809 \text{ (años}^2)\] \[{S_Y^2}=\frac{\displaystyle\sum_{i=1}^{n}(y_i-\bar{y})^2}{n-1}=\frac{10,000}{15-1}=7,142.8571 \text{ (euros}^2)\]

Para calcular la covarianza vamos a utilizar la Ecuación 2.7:

\[S_{XY}=\frac{\displaystyle\sum_{i=1}^{n}\left ( x_i - \bar{x} \right )\cdot\left ( y_i - \bar{y}\right )}{n-1}\]

Para calcular el sumatorio del numerador añadimos a la Tabla 2.20 la columna 7, que será el producto de las columnas 3 y 4. Una vez calculada la columna, sumamos todos los valores. Obtenemos que: \[\displaystyle\sum_{i=1}^{n=15}\left ( x_i - \bar{x} \right )\cdot\left ( y_i - \bar{y}\right )=900\]

Por tanto, la covarianza será: \[S_{XY}=\frac{\displaystyle\sum_{i=1}^{n=15}\left ( x_i - \bar{x} \right )\cdot\left ( y_i - \bar{y}\right )}{n-1}=\frac{900}{15-1}=64.2857\hspace{1mm}(\text{años}\cdot euros)\]

Ejemplo 2.10. con Excel. El cálculo de la covarianza con Excel podemos hacerlo con las funciones:

COVARIANZA.M(): devuelve la covarianza de la muestra (Ecuación 2.7)
COVARIANCE.P(): devuelve la covarianza de la población (Ecuación 2.11)

Observad que para poder hacer uso de las funciones de Excel los datos no pueden estar resumidos de forma que tengamos las frecuencias de repetición de los pares de valores. En este caso tendríamos que calcular una especie de covarianza poderada, y Excel no lo permite.

Abrimos el fichero de Excel ej_2_2.xlsx. Por ejemplo, nos situamos en la celda E9 y escribimos covarianza muestral. En la celda F9 introducimos la fórmula: =covarianza.m(B2:B16;C2:C16). La covarianza (muestral) es 64.2857 ($años \text{ x } euros$)

Guardad el libro Excel con el nombre ej_2_10_1.

En la animación que encontrarás en [https://www.uv.es/ticstat/ej_2_10_1.gif](https://www.uv.es/ticstat/ej_2_10_1.gif) puedes ver cómo calcular la covarianza con Excel.

Sólo por practicar, también podemos calcular la covarianza en Excel reproduciendo los pasos de cálculo que hemos realizado en el ejemplo 2.10.

Abrimos el archivo de Excel datos_tema_2.xlsx.

En el rango de celdas D1:H1escribimos los siguientes encabezamientos de columna:

x-medx para representar $x_i-\bar{x}$
y-medy para representar $y_i-\bar{y}$
(x-medx)^2 para representar $(x_i-\bar{x})^2$
(y-medy)^2 para representar $(y_i-\bar{y})^2$
(x-medx)(y-medy) para representar $(x_i-\bar{x})(y_i-\bar{y})$

En el rango A18:A23 escribimos:

tamaño n
media x
media y
varianza x
varianza y
covarianza xy

Calculamos el tamaño de la muestra, la media de X y la media de Y en el rango B18:B20.

Recuerda que puedas calcular el tamaño de la muestra con la función CONTAR() y las medias con la función PROMEDIO().

Vamos a redondear los resultados a 4 decimales; para ello utilizaremos la función de Excel: REDONDEAR(). Esta función tiene dos argumentos, el primero es el valor a redondear, el segundo el número de decimales a utilizar en el redondeo.

Indroducimos en las siguientes celdas las fórmulas para reproducir los cálculos intermedios realizado en el ejemplo 2.9.

celda D2: =redondear(B2-$B$19;4)
celda E2: =redondear(C2-$B$20;4)
celda F2: =redondear(D2^2;4)
celda G2: =redondear(E2^2;4)
celda H2: =redondear(D2*E2;4)

Calculamos también las sumas de las columnas F:H porque representarán los numeradores de las varianzas y de la covarianza.

Ya estamos en disposición de calcular las medidas de interés. En la celda B21 introducimos la fórmula =F17/(B18-1) para calcular la varianza de X; en la celda B22 calculamos la varianza de Y con la expresión =G17/(B18-1) y, por útlimo, la covarianza la calculamos haciendo que la celda B23 sea =H17/(B18-1)

Guardad el libro Excel con el nombre ej_2_10_2.

En la animación que encontrarás en [https://www.uv.es/ticstat/ej_2_10_2.gif](https://www.uv.es/ticstat/ej_2_10_2.gif) puedes ver cómo realizar los cálculos intermedios con Excel para calcular la covarianza.

En ocasiones, los datos vienen estructurados de forma que los $K$ pares de puntos $(x_i,y_i),\hspace{1mm}i={1,2,...,K}$ se repiten $n_i$ veces. Sería una estructura de datos como la que se muestra en la Tabla 2.21:

Tabla 2.21: Estructura de datos en la que los pares $(x_i,y_i)$ se repiten.

Observación	$x_i$	$y_i$	$n_i$
1	$x_1$	$y_1$	$n_1$
2	$x_2$	$y_2$	$n_2$
$\vdots$	$\vdots$	$\vdots$	$\vdots$
i	$x_i$	$y_1$	$n_i$
$\vdots$	$\vdots$	$\vdots$	$\vdots$
K	$x_K$	$y_K$	$n_K$

En estos casos, la expresión para calcular la covarianza muestral debe considerar las frecuencias, como se recoge en la Ecuación 2.9. Sería como calcular una covarianza ponderada.\[S_{XY}=\frac{\displaystyle\sum_{i=1}^{K}\left ( x_i - \bar{x} \right )\cdot\left ( y_i - \bar{y}\right ) \cdot n_i}{n-1} \tag{2.9}\]

Ejemplo 2.10 Los datos de nuestra muestra de 15 empleados, relativos a su Experiencia (variable X) y Salario (variable Y) (ver Tabla 2.1), podemos resumirlos como se muestra a continuación:

Tabla 2.22: Datos de 15 empleados. Los pares $(x_i,y_i)$ se repiten.

$x_i$	$y_i$	$n_i$
2	1,200	4
2	1,300	1
3	1,200	1
3	1,300	3
4	1,300	1
4	1,400	5

En esta situación, calcular la covarianza entre Experiencia y Salario.

Solución: Como tenemos un total de 6 pares de datos ($K=6$) y se repiten, haremos uso de la siguiente expresión para calcular la covarianza: \[S_{XY}=\frac{\displaystyle\sum_{i=1}^{K=6}\left ( x_i - \bar{x} \right )\cdot\left ( y_i - \bar{y}\right ) \cdot n_i}{n-1}\] Vamos a construir una tabla que recoja los cálculos necesarios.

Realizamos los cálculos utilizando 4 decimales. Es muy importante ajustar la precisión de los cálculos en función del contexto del problema.

Tabla 2.23: Tabla de cálculos intermedios para la covarianza.

$x_i$	$y_i$	$n_i$	$x_i\cdot n_i$	$x_i\cdot n_i$	$x_i-\bar{x}$	$y_i-\bar{y}$	$(x_i-\bar{x})\cdot(y_i-\bar{y})\cdot n_i$
2	1,200	4	8	4,800	-1.0667	-100	426.60
2	1,300	1	2	1,300	-1.0667	0	0
3	1,200	1	3	1,200	-0.0667	-100	6.67
3	1.300	3	9	3,900	-0.0667	0	0
4	1,300	1	4	1,300	0.9333	0	0
4	1,400	5	20	7,000	0.9333	100	466.65
		—	—	—			—
		$\sum=15$	$\sum=46$	$\sum=19,500$			$\sum=900$

Una vez hemos construido la tabla con los cálculos intermedios, procedemos a obtener las medidas de interés.

\[\bar{x}=\frac{\displaystyle\sum_{i=1}^{K=6}x_i\cdot n_i}{n}=\frac{46}{15}=3.0667\hspace{1mm}\text{años}\]

\[\bar{y}=\frac{\displaystyle\sum_{i=1}^{K=6}y_i\cdot n_i}{n}=\frac{19,500}{15}=1,300\hspace{1mm}\text{euros}\]

\[S_{XY}=\frac{\displaystyle\sum_{i=1}^{6}\left ( x_i - \bar{x} \right )\cdot\left ( y_i - \bar{y}\right ) \cdot n_i}{n-1}=\frac{900}{15-1}\approx 64.2857\hspace{1mm}(\text{años}\cdot euros)\]

Ejemplo 2.11. con Excel. Cuando los datos están dispuestos como se muestra en la Tabla 2.21 no tenemos una función en Excel que calcule lo que sería una covarianza ponderada. Así pues, tenemos que construirnos la tabla de cálculo, similar a la realizada en el Ejemplo 2.10.

Abrimos un nuevo libro de Excel y reproducimos en el rango A1:C7 el contenido de la Tabla 2.22.

En el rango A10:A12 escribimos, respectivamente, medx, medy y covarxy. En el rango D1:F1 escribiremos:

xi-medx para representar $x_i-\bar{x}$
yi-medy para representar $y_i-\bar{y}$
(xi-medx)(yi-medy)ni para representar $(x_i-\bar{x})\cdot (y_i-\bar{y})\cdot n_i$

En la celda C8 calculamos el número total de observaciones (tamaño de la muestra) sumando el rango C2:C7.

En la celda B10 introducimos la fórmula =sumaproducto(A2:A7;C2:C7)/C7 para calcular la media de la variable X. De forma análoga calculamos la media de Y.

En la celda D2 escribimos la fórmula =A2-$B$10; en la celda E2 la fórmula =B2-$B$11; y en la celda F2: =D2*E2*C2.

Seleccionamos el rango D2:F2 y arrastramos hasta la fila 7.

Si sumamos los valores de la columna F tendríamos el numerador de la Ecuación 2.9; por tanto, en la celda F8 sumamos los valores de la columna introduciendo la fórmula: =suma(F2:F7). La suma de los productos de las desviaciones de cada variable respecto de su respectiva media es 900. Ya podemos calcular el valor de la covarianza en la celda B12, que será el resultado de dividir el valor de la celda F8 entre el tamaño de la muestra menos 1, es decir, en la celda B12 escribiremos la fórmula: =F8/(C8-1).

La covarianza es aproximadamente igual $64.2857\hspace{1mm}(\text{años}\cdot euros)$.

Guardad el libro Excel con el nombre ej_2_11.

En la animación que encontrarás en [https://www.uv.es/ticstat/ej_2_11.gif](https://www.uv.es/ticstat/ej_2_11.gif) puedes ver cómo se ha resuelto este ejemplo para calcular la covarianza.

Aunque resultaría de una situación bastante teórica, también podemos calcular la covarianza a partir de una tabla de doble entrada, como la que se muestra en las Tabla 2.4. Para elle deberíamos considerar que cada par $(x_i,y_j)$ con $i={1,2,...,I}$ y $j={1,2,...,J}$ se repite $n_{ij}$ veces. En esta situación I es el número de distintos valores que toma la variable X, y J los que toma la variable Y. La covarianza la calcularíamos mediante la siguiente expresión:\[S_{XY}=\frac{\displaystyle\sum_{i=1}^{I}\sum_{j=1}^{J}\left ( x_i - \bar{x} \right )\cdot\left ( y_i - \bar{y}\right ) \cdot n_{ij}}{n-1} \tag{2.10}\]

La covarianza poblacional se denota por $\sigma_{XY}$ y su expresión es:

\[\sigma_{XY}=\frac{\displaystyle\sum_{i=1}^{N}\left ( x_i - \mu_X \right )\left ( y_i - \mu_Y \right )}{N} \tag{2.11}\]

Si se parte de una tabla de frecuencias como la Tabla 2.21, entonces la expresión equivalente es:

\[\sigma_{XY}=\frac{\displaystyle\sum_{i=1}^{K}\left ( x_i - \mu_X \right )\cdot\left ( y_i - \mu_Y\right ) \cdot n_i}{N} \tag{2.12}\]

y en el caso realizar el cálculo a partir de una tabla de doble entrada:

\[\sigma_{XY}=\frac{\displaystyle\sum_{i=1}^{I}\sum_{j=1}^{J}\left ( x_i - \mu_X \right )\cdot\left ( y_j - \mu_Y\right ) \cdot n_{ij}}{N} \tag{2.13}\]

2.5.1 Intepretación de la covarianza.

La covarianza es una medida de cómo varían conjuntamente las variables X e Y respecto de sus respectivas medias. Si una variable crece o decrece respecto de su media, ¿qué le ocurre a la otra variable? En la Figura 2.12 se han representado dos diagramas de dispersión en los que se ha dibujado:

la media de la variable X (línea discontínua vertical) y la media de la variable Y (línea discontinua horizontal).
en color rojo se han representado las observaciones en las que el producto $(x_i-\bar{x})\cdot (y_i-\bar{y})$ es negativo.
en color azul se han representado las observaciones en las que el producto $(x_i-\bar{x})\cdot (y_i-\bar{y})$ es positivo.

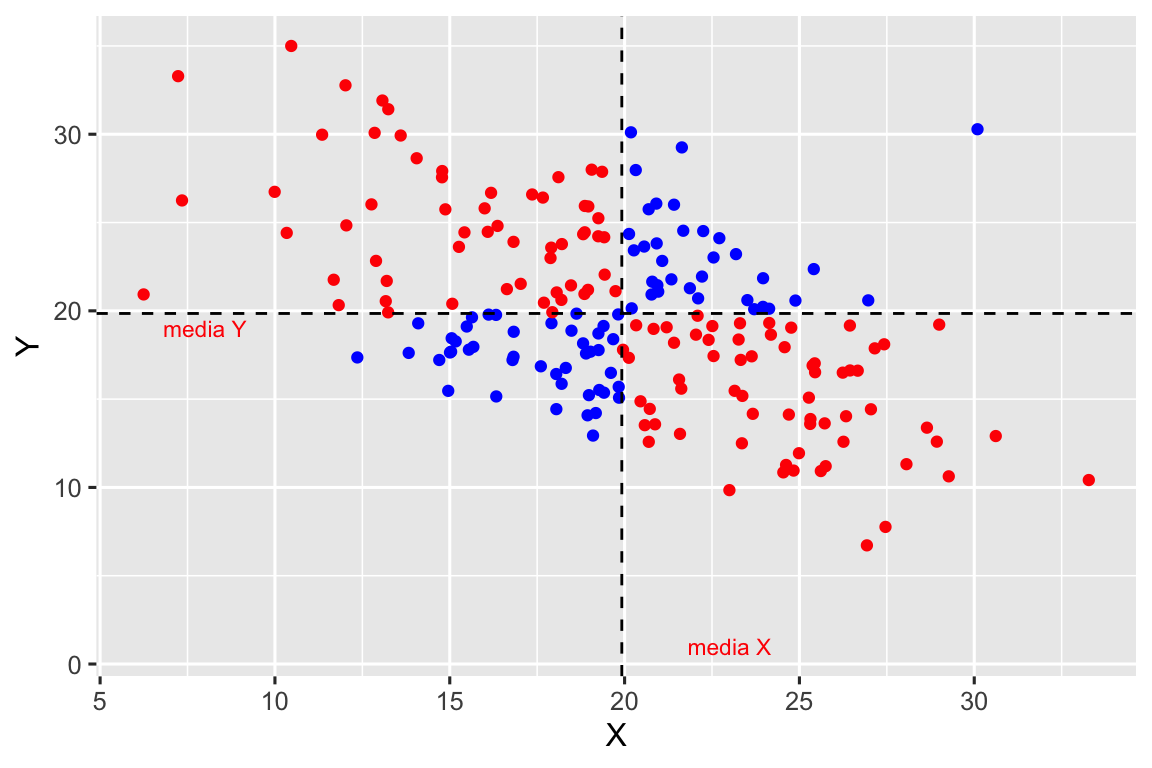
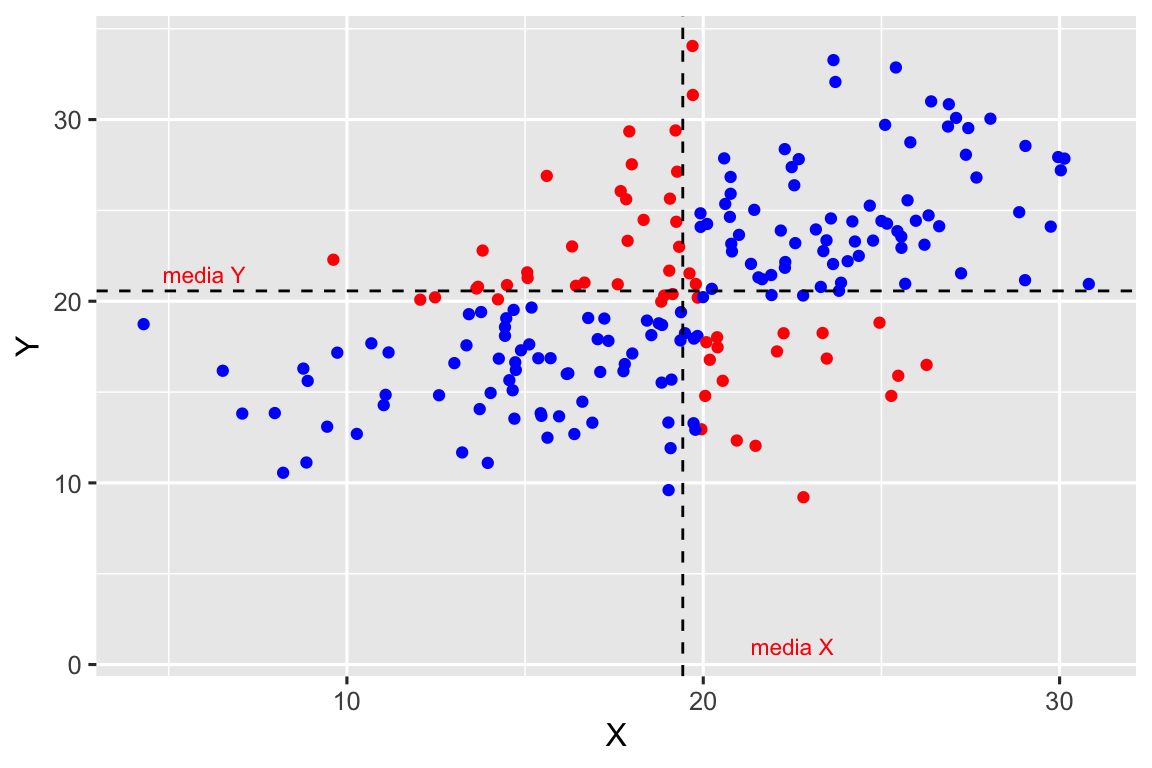
Si hay muchas mas observaciones de color rojo que de color azul entonces, en general, la suma de los productos $(x_i-\bar{x})\cdot (y_i-\bar{y})$ será negativa y, por tanto, la covarianza será negativa. En general, valores elevados de la variable X se relacionan con valores bajos de la variable Y, y valores bajos de X con valores elevados de Y.

Por el contrario, si dominan las observaciones de color azul entonces la suma de los productos $(x_i-\bar{x})\cdot (y_i-\bar{y})$ será positiva y, en consecuencia, la covarianza será positiva. Podemos observar como en esta situación, valores elevados de una variable se asocian con valores elevados de la otra variable y lo mismo sucede con los valores bajos. Importante, no todos los valores siguen este comportamiento, por eso se habla siempre en términos de: en media.

A la hora de interpretar la covarianza, interesa conocer su signo o si es cero. No interesa la magnitud de la covarianza porque es una medida que depende de los cambios de escala o unidad , es decir, la covarianza depende de las unidades en las que se encuentran medidas las variables. Por esta razón, para analizar la intensidad de la relación lineal se utiliza una medida adimensional, el coeficiente de correlación lineal (Sección 2.6).

Interpretación general del significado de la covarianza:

Si la covarianza es positiva ($S_{XY}>0$): Observamos una relación lineal positiva entre las variables X e Y. En media, si crece/decrece X, también crece/decrece Y. Las variables covarían en la misma dirección respecto de sus medias. La nube de puntos del diagrama de dispersión es ascendente; la mayor parte de los pares de puntos se sitúan en los cuadrantes II y IV del diagrama.
Si la covarianza es negativa ($S_{XY}<0$): Observamos una relación lineal negativa entre las variables X e Y. En media, si crece/decrece X, la variable Y decrece/crece. Las variables covarían en sentido contrario respecto de sus medias. La nube de puntos del diagrama de dispersión es descendente; la mayor parte de los pares de puntos se sitúan en los cuadrantes I y III del diagrama.
Si la covarianza es cero ($S_{XY}=0$) puede ser porque:
- las variables son independientes. Si X e Y no tienen ninguna relación entonces necesariamente la covarianza, que mide el sentido de una relación lineal, será cero.
- las variables están relacionadas pero no linealmente. Por ejemplo, en la Figura 2.13 se observa un gráfico de dispersión en el que claramente se observa que existe relación entre X e Y; sin embargo, la covarianza es cero.

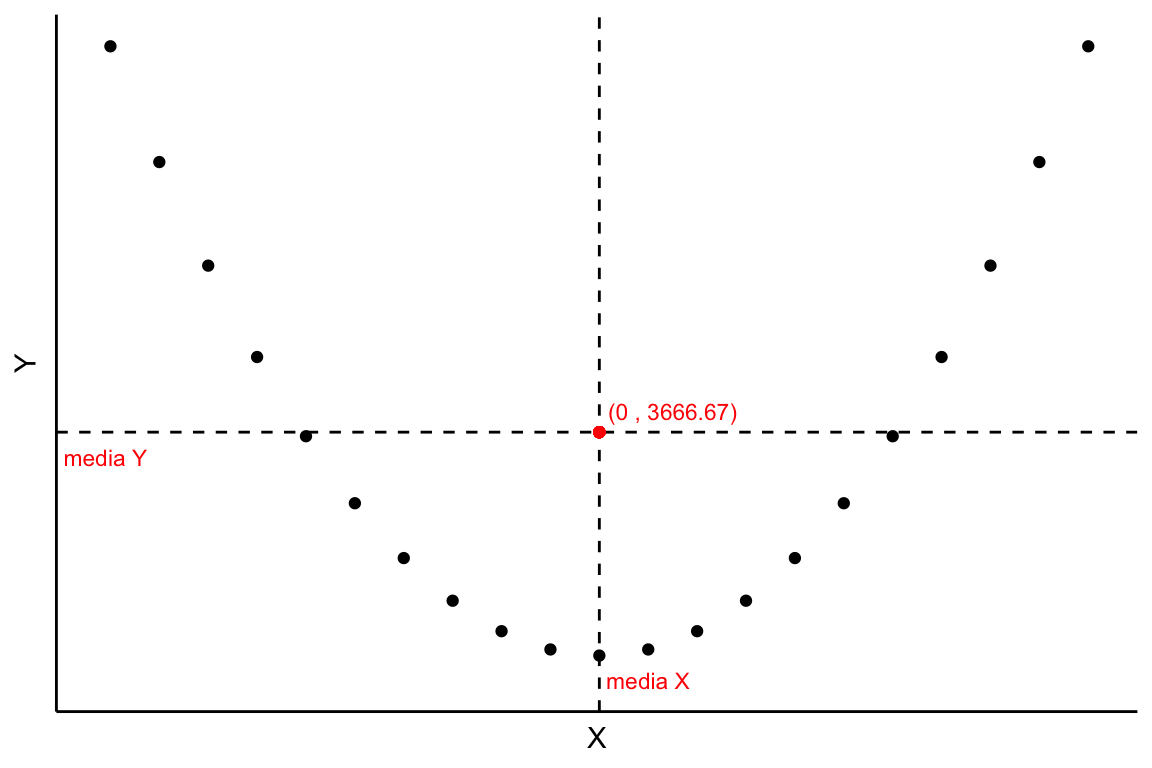
Figura 2.13: Covarianza nula pero variables relacionadas.

Si dos variables X e Y son independientes entonces su covarianza es cero, pero si la covarianza es cero las variables no tienen por qué ser independientes. La covarianza nula indica no relación lineal.

Cuando digo cero, no es cero exacto. En inferencia estadística hablamos en los siguientes términos: “es estadísticamente distinto de cero” o “es significativamente distinto de cero”. También comprobaremos la relación lineal entre dos variables cuantitativas aplicando el contraste de hipótesis de incorrelación.

Ejemplo 2.11 En ejemplos anteriores hemos obtenido que la covarianza entre la Experiencia y el Salario era de 64.2857 (años$\cdot$euros). Interpreta este resultado.

Solución: El resultado $S_{XY}\approx 64.2857$ indica que parece existir (cierta) relación lineal positiva entre experiencia y salario; es decir, en media, cuanto mayor es la experiencia de los empleados, mayor es también el salario. Excede el alcance de este manual, pero en la práctica aplicaríamos el contraste de incorrelación para confirmar nuestra primera aproximación sobre la interpretación de la covarianza.

Recuerda que la covarianza es una medida de la asociación/relación lineal entre dos variables cuantitativas y su signo nos indica cómo varían conjuntamente respecto de sus correspondientes medias.

2.5.2 Matriz de varianzas-covarianzas

La matriz de varianzas-covarianzas, que denotamos por $V$, es una matriz cuadrada de dimensión $(k\text{x}k)$, donde $k$ es el número de variables analizadas. En esta matriz, los elementos de la diagonal principal son las varianzas de las variables y el resto de elementos las covarianzas entre cada par de variables.

Consideremos que estamos trabajando con tres variables ($X$, $Y$, $Z$), la matriz de varianzas-covarianzas sería:\[ V=\begin{pmatrix} {S^2_X} & S_{XY} & S_{XZ}\\ S_{YX}& {S^2_Y} & S_{YZ} \\ S_{ZX} & S_{ZY} & {S^2_Z} \end{pmatrix} \tag{2.14}\] Como, por ejemplo, la covarianza entre $X$ e $Y$ es la misma que la covarianza entre $Y$ y $X$ ($S_{XY}=S_{YX}$), la matriz de varianzas-covarianzas es simétrica. Por esta razón, en muchas aplicaciones únicamente se proporciona la diagonal principal y la parte superior o inferior de la matriz.\[ V=\begin{pmatrix} {S^2_X} & S_{XY} & S_{XZ}\\ & {S^2_Y} & S_{YZ} \\ & & {S^2_Z} \end{pmatrix} \hspace{5mm} \text{o alternativamente} \hspace{5mm}V=\begin{pmatrix} {S^2_X} & & \\ S_{YX}& {S^2_Y} & \\ S_{ZX} & S_{ZY} & {S^2_Z} \end{pmatrix}\] Por último, comentar que la matriz de varianzas-covarianzas es semidefinida positiva. Esto quiere decir que el determinante de la matriz es mayor o igual a cero ($|V|\geq0$).

Si en lugar de trabajar con una muestra trabajamos con la población, tendremos la matriz de varianzas-covarianzas poblacional, que se denota por $\Sigma$. \[\Sigma =\begin{pmatrix} \sigma^2_X & \sigma_{XY} & \sigma_{XZ}\\ \sigma_{YX}& \sigma^2_Y & \sigma_{YZ} \\ \sigma_{ZX} & \sigma_{ZY} & \sigma^2_Z \end{pmatrix} \tag{2.15}\]

2.6 Teoría de la correlación

La covarianza mide el sentido de la relación lineal entre dos variables cuantitativas X e Y. Para evaluar la fortaleza o intensidad de la relación lineal se utiliza el coeficiente de correlación lineal de Pearson.

El coeficiente de correlación (lineal) muestral se denota por $r_{XY}$ y se define como: \[r_{XY}=\frac{S_{XY}}{S_X \cdot S_Y} \tag{2.16}\]

El coeficiente de correlación es una medida adimensional, no depende de los cambios de origen ni de escala, y se encuentra acotado entre -1 y 1.

\[-1\leq r_{XY} \leq 1 \tag{2.17}\]

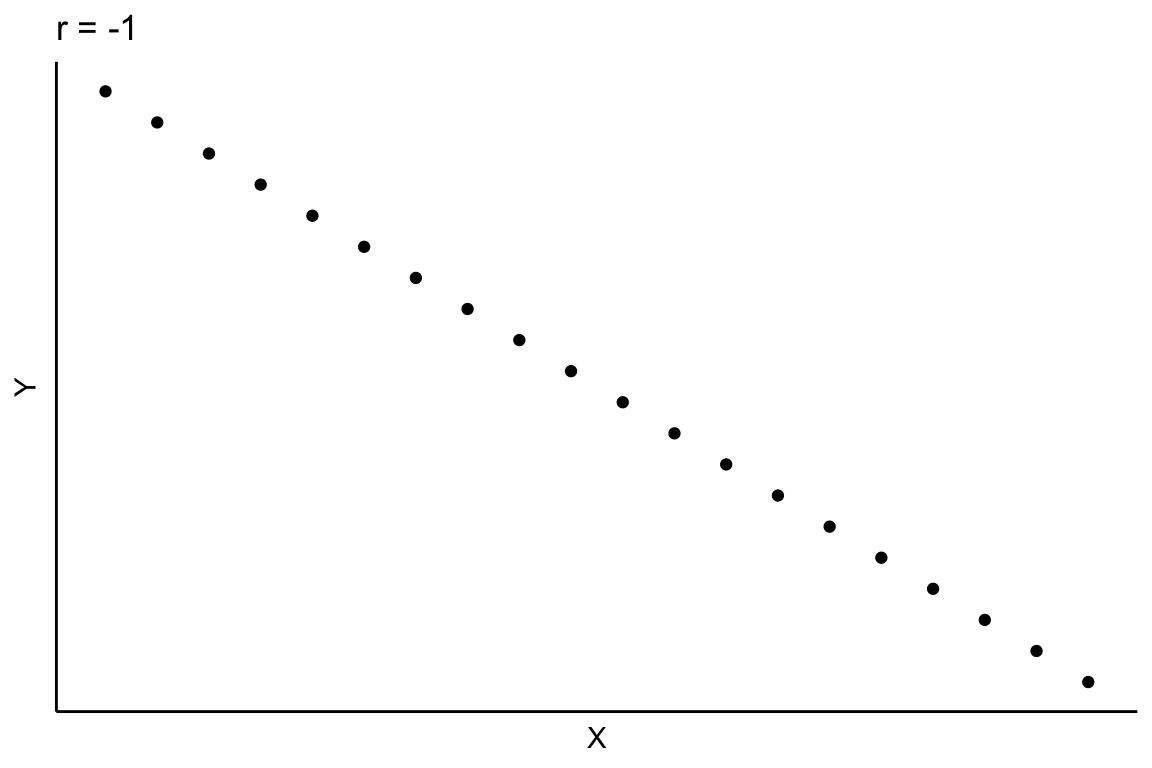
2.6.1 Interpretación del coeficiente de correlación

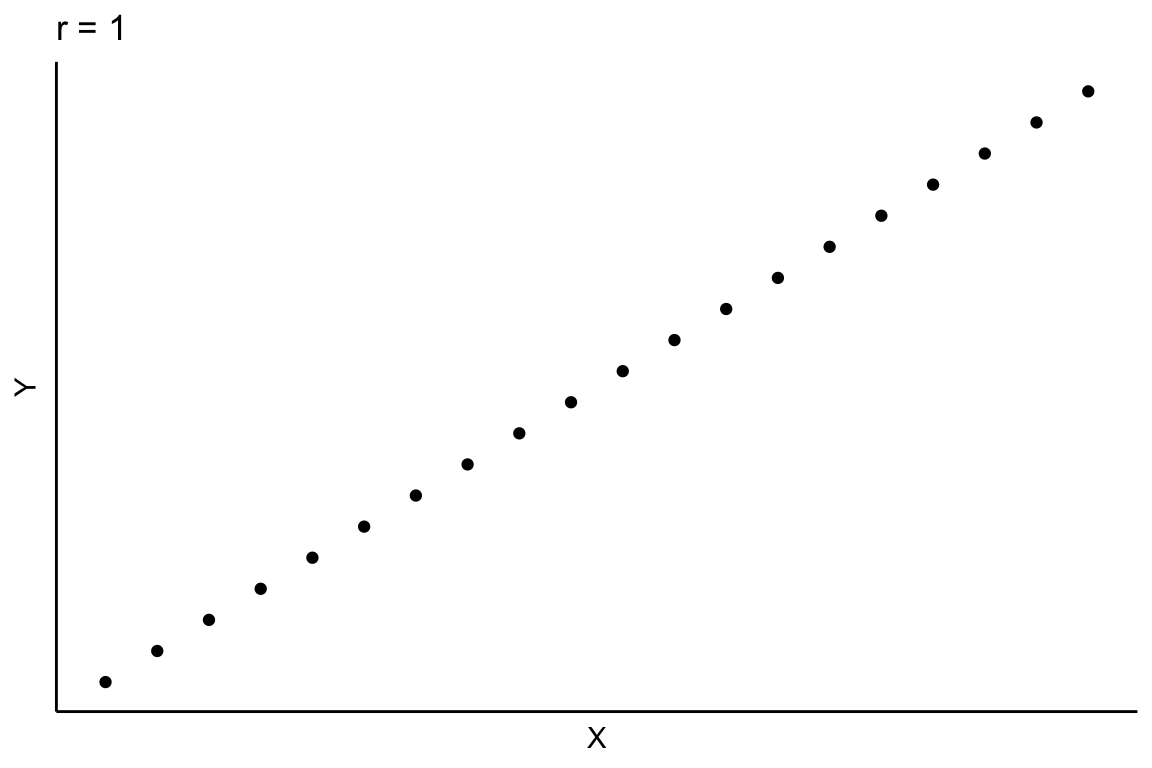
En la Figura 2.14 se han representado varios casos que nos permitirán interpretar el valor que toma el coeficiente de correlación lineal.

$r_{XY} = -1$ (Figura 2.14.a), la relación lineal entre las variables X e Y es perfecta negativa.
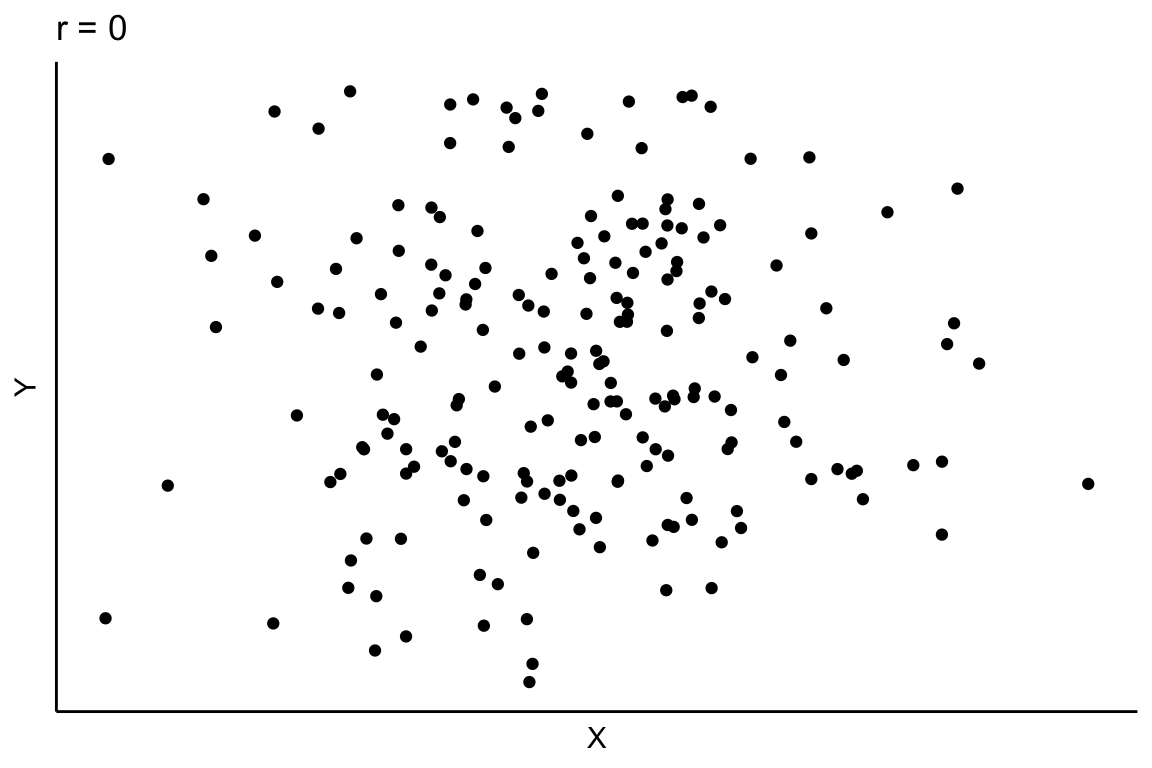
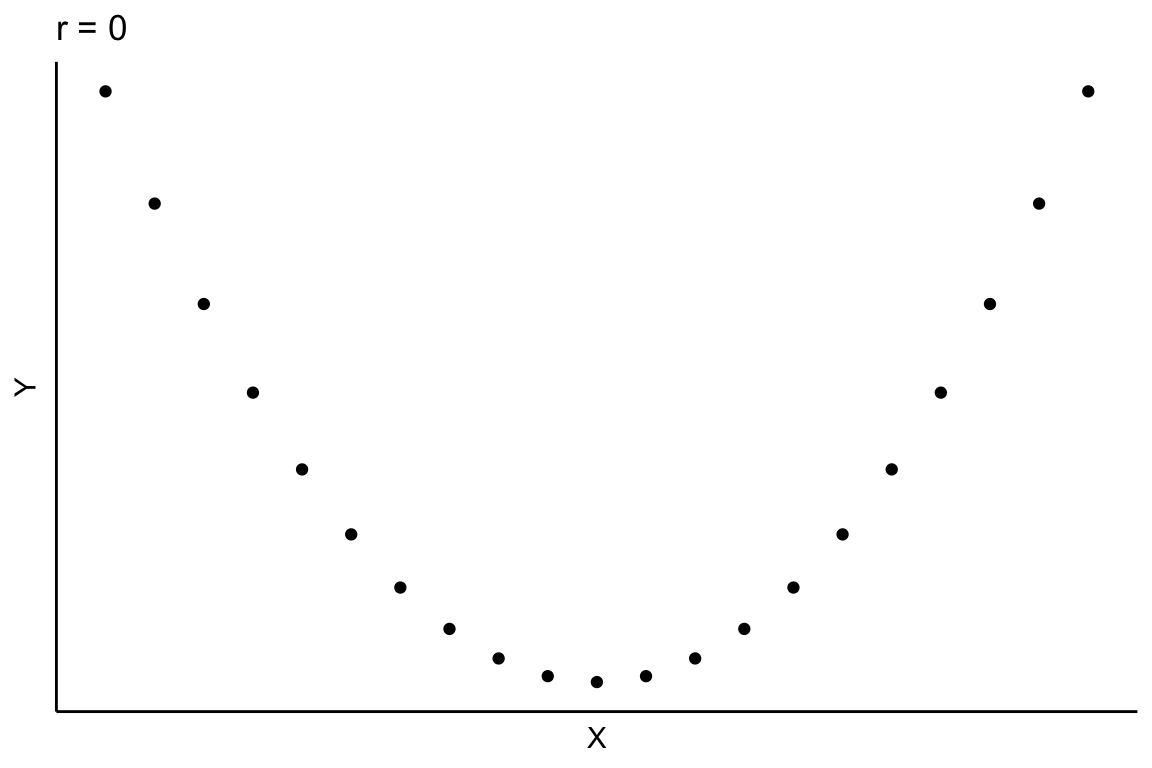
$r_{XY} \approx 0$ (es cero o muy próximo a cero), no existe relación lineal entre las variables X e Y (la covarianza será cero), es el caso de la Figura 2.14.c. Esto no significa que las variables sean independentes, la relación puede ser de otro tipo (parabólica, exponencial, potencial, etc.), como se observa en la Figura 2.14.d. Para determinar si la correlación es estadísticamente significativa (significativamente distinta de cero) podemos utilizar la siguiente aproximación: si el coeficiente de correlación es, en valor absoluto, mayor a $2/\sqrt{n}$, la correlación es estadísticamente significativa.
$r_{XY} = 1$, la relación lineal entre las variables X e Y es perfecta positiva (Figura 2.14.b).

En general, podemos evaluar el grado de la fortaleza de la relación lineal tal y como se recoge en la Tabla 2.24.

Tabla 2.24: Interpretación general del valor del coeficiente de correlación lineal.

$-0.25<r_{XY} < 0$	Muy débil	$0<r_{XY} < 0.25$
$-0.6<r_{XY} \leq -0.25$	Débil	$0.25 \leq r_{XY} < 0.6$
$-0.8<r_{XY} \leq -0.6$	Relativamente fuerte	$0.6 \leq r_{XY} < 0.8$
$-1<r_{XY} \leq -0.8$	Fuerte	$0.8 \leq r_{XY} < 1$

y podemos hacer uso de la aproximación Newbold, Carlson, y Thorne. (2010): \[|r_{XY}|> \frac{2}{\sqrt{n}} \tag{2.18}\]

para determinar si el coeficiente de correlación obtenido es estadísticamente significativo, equivalente a decir que es significativamente distinto de cero.

La significatividad del coeficiente de correlación depende del tamaño de la muestra (n). Esto quiere decir que con muestras pequeñas podemos obtener coeficientes de correlación altos pero no significativos y al contrario, con muestras grandes tener coeficientes bajos pero significativos.

El coeficiente de correlación poblacional se denota por $\rho$, y se define como: \[\rho=\frac{\sigma_{XY}}{\sigma_X \cdot \sigma_Y} \tag{2.19}\] Naturalmente, $-1\leq \rho\leq 1$

2.6.2 Matriz de correlación

La matriz de correlación, que se denota por $R$, es una matriz cuadrada cuya diagonal está formada por unos y el resto de elementos son las correlaciones entre cada para de variables. Como $r_{XY}=r_{YX}$, la matriz de correlación es simétrica.

La matriz de correlación de tres variables ($X$, $Y$, $Z$) sería:\[R=\begin{pmatrix} {r^2_X} & r_{XY} & r_{XZ}\\ r_{YX}& {r^2_Y} & r_{YZ} \\ r_{ZX} & r_{ZY} & {r^2_Z} \end{pmatrix} \tag{2.20}\]

Si en lugar de trabajar con una muestra trabajamos con la población, tendremos la matriz de correlación poblacional. \[P =\begin{pmatrix} 1 & \rho_{XY} & \rho_{XZ}\\ \rho_{YX}& 1 & \rho_{YZ} \\ \rho_{ZX} & \rho_{ZY} & 1 \end{pmatrix} \tag{2.21}\]

Ejemplo 2.12 Resume los resultados obtenidos de la Experiencia y el Salario de la muestra de 15 empleados analizados en el vector de medias, la matriz de varianzas-covarianzas y la matriz de correlación.

Solución: Como sabemos, para los 15 empleados analizados, la media de experiencia es aproximadamente 3.0667 años y el salario medio es 1,300 euros.

Denotando X: “Experiencia (en años)” y Y: “Salario (en euros)”, el vector de medias será: \[ \bar{m} =\begin{pmatrix} \bar{x}\\ \bar{y}\\ \end{pmatrix} = \begin{pmatrix} 3.0667\\ 1,300\\ \end{pmatrix} \] En ejercicios anteriores hemos calculado las varianzas de las variables implicadas así como la covarianza. Estos resultados podemos resumirlos en la matriz de varianzas-covarianzas: \[V=\begin{pmatrix} {S^2_X} & S_{XY} \\ S_{YX} & {S^2_Y} \end{pmatrix}=\begin{pmatrix} 0.7809 & 64.2857 \\ 64.2857 & 7,142.8571 \end{pmatrix}\] aunque al ser simétrica es muy frecuente expresar la matriz $V$ como: \[V=\begin{pmatrix} {S^2_X} & S_{XY} \\ & {S^2_Y} \end{pmatrix}=\begin{pmatrix} 0.7809 & 64.2857 \\ & 7,142.8571 \end{pmatrix}\] La covarianza nos indica una (posible) asociación/relación lineal positiva entre la experiencia y el salario. En media, empleados con mayor experiencia obtienen mayores salarios. Ahora bien, ¿cómo de fuerte o intensa es esta relación?

Para responder a esta cuestión calculamos el coeficiente de correlación lineal: \[r_{XY}=\frac{S_{XY}}{S_X \cdot S_Y}=\frac{64.2857}{\sqrt{0.7809}\cdot\sqrt{7,142.8571}}=\frac{64.2857}{74.6851}\approx0.8608\] ¿Es estadísticamente significativa esta relación lineal?

Una aproximación al contraste de hipótesis de la correlación, que se estudiará en inferencia estadística, es utilizar la expresión dada en la Ecuación 2.18. \[|r_{XY}|> \frac{2}{\sqrt{n}} \qquad r_{XY}=0.8601 > \frac{2}{\sqrt{15}}=0.5164\] Por tanto, podemos decir que se observa una fuerte relación lienal positva entre experiencia y salario en el conjunto de datos analizado.

La matriz de correlación la podemos expresar de la siguiente forma: \[R=\begin{pmatrix} {r^2_X} & r_{XY}\\ & {r^2_Y} \end{pmatrix}= \begin{pmatrix}1 & 0.8608\\ & 1 \end{pmatrix}\]

Ejemplo 2.13. con Excel. En la herramientas de análisis de datos de Excel tenemos la función Covarianza, que calcula la matriz de varianzas-covarianzas poblacional; por tanto, si estamos trabajando con una muestra y usamos esta funcionalidad, estaríamos cometiendo un error. En herramientas de análisis también está disponible la función Coeficiente de correlación que devuelve la matriz de correlación.

Como el uso de la función Covarianza y Coeficiente de correlación es idéntico, vamos a calcular la matriz de correlación para tener una idea clara de la fortaleza de la relación lineal entre Experiencia y Salario.

Abrimos el fichero de Excel ej-2-10-1.xlsx.

Nos situamos en la celda E11 y seleccionamos Datos > Análisis de Datos > Coeficiente de correlación y Aceptar. Se abre el cuadro de diálogo que se reproduce en la Figura 2.15 una vez cumplimentados los datos. Como se observa, se ha seleccionado como rango de datos el rango B1:C17, y como incluye los encabezados marcamos la opción Rótulos en la primera fila. El resultado de la función queremos que lo devuelva en la celda E11.

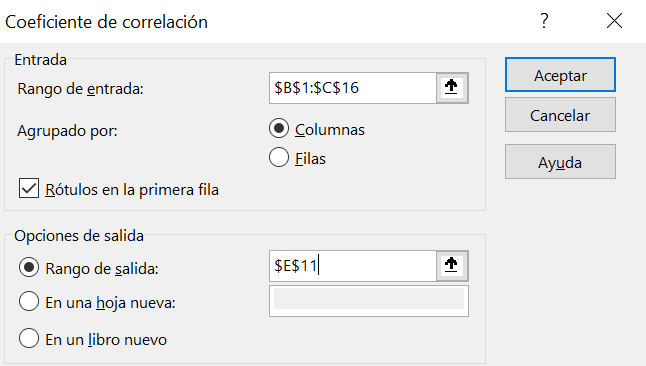
Figura 2.15: Análisis de datos: Opciones de Coeficiente de correlación.

Al clicar en Aceptar Excel devolverá la matriz de correlación. El resultado final debería ser el mostrado en la Figura 2.16.

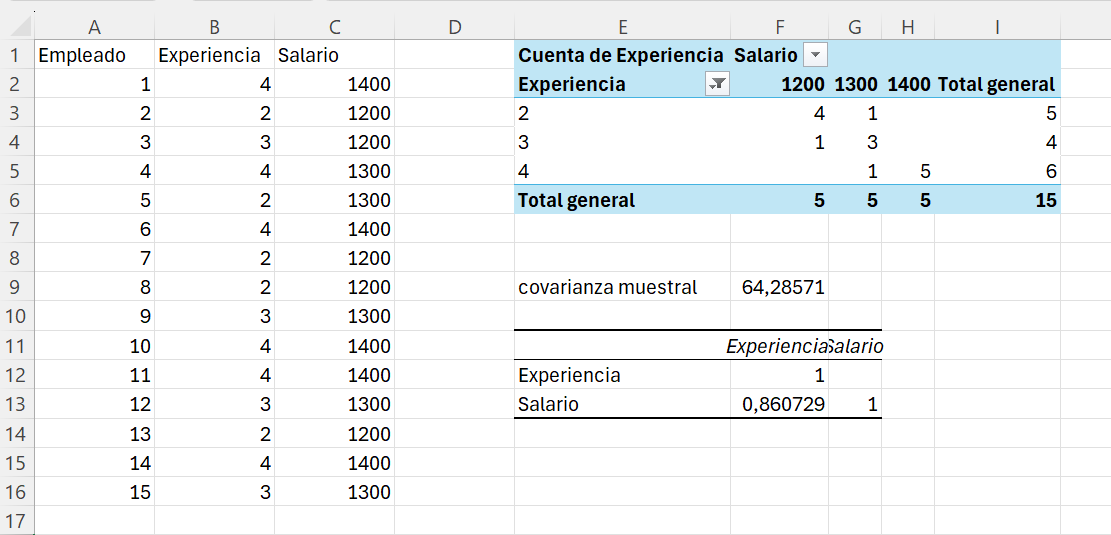
Figura 2.16: Análisis de datos: Matriz de correlación.

Guardar el fichero con el nombre ej-2-13.

En la animación que encontrarás en [https://www.uv.es/ticstat/ej_2_13.gif](https://www.uv.es/ticstat/ej_2_13.gif) puedes ver cómo se ha resuelto este ejemplo para calcular la covarianza.

Recuerda que la función Covarianza de Análisis de datos devuelve la matriz de varianzas-covarianzas poblacionales.

2.7 Asociación y concordancia

La covarianza y el coeficiente de correlación son medidas de la asociación lineal entre variables cuantitativas. Sin embargo, en el campo de las Ciencias Sociales es frecuente trabajar con variables de naturaleza cualitativa. En estos casos, ¿cómo podemos evaluar la asociación o relación entre las variables? Si las dos variables son categóricas, la asociación entre ellas puede ser de atracción o de repulsión, según la frecuencia sea mayor o menor a la que cabe esperar si fueran independientes. Para facilitar la interpretación de la asociación entre atributos es frecuente recurrir al uso de medidas estadísticas específicas para variables cualitativas, tales como:

Coeficiente de contingencia $\chi^2$.
Coeficiente de contingencia $C$ de Pearson.
Coeficiente de contingencia $V$ de Cramer.
Concordancia o correlación ordinal.

2.7.1 Coeficiente de contingencia $\chi^2$.

Este coeficiente se basa en la comparación de las frecuencias conjuntas observadas ($n_{ij}$) y las frecuencias que teóricamente ($n^T_{ij}$) cabría observar en el caso de que las dos variables categóricas fueran independientes (ver Sección 2.4) . El coeficiente de contigencia $\chi^2$ tiene la siguiente expresión: \[\chi^2 = \displaystyle \sum_{i=1}^{I} \sum_{j=1}^{J} \frac{(n_{ij}-n^T_{ij})^2}{n^T_{ij}} \tag{2.22}\]

Como puede observarse en la expresión dada por la Ecuación 2.22, la diferencia entre las frecuencias conjuntas observadas y teóricas se encuentra elevadas al cuadrado para evitar que diferencias positivas se anulen con diferencias negativas, por esta razón el grado de divergencia entre los valores observados y teóricos se formula a través de la convergencia cuadrática.

Si las variables son independientes entonces necesariamente $\chi^2=0$, las frecuencias observadas y teóricas coincidirán ($n_{ij}=n^T_{ij}$).

Si existe algún grado de asociación entre los atributos entonces el valor del coeficiente de contingencia será positivo ($\chi^2>0$). De forma que cuanto mayor sea el valor del estadístico $\chi^2$, más intenso será el grado de asociación entre las variables.

El principal inconveniente de esta medida de la asociación entre dos atributos es que su valor no está acotado superiormente.

Ejemplo 2.13 A partir de los datos del Barómetro de del CIS se ha obtendio la siguiente tabla de contingencia entrelos efectos de la COVID-19 y el sexo.

Tabla 2.25: Tabla contingencia obtenida del efecto COVID-19 y el sexo.

Sexo/Efecto	Salud	Economía	Ambos	Ninguno	No sabe	No contesta	$n_{i\bullet}$
Hombre	636	840	397	13	5	5	1,896
Mujer	664	672	617	8	3	0	1,964
$n_{\bullet j}$	1,300	1,512	1,014	21	8	5	n=3,860

Nos planteamos cuantificar el grado de asociación entre los efectos más preocupantes de la COVID-19 y el sexo de la persona entrevistada.

Solución: Como las variables no son independientes (podéis comprobarlo haciendo uso del teorema de caracterización (Sección 2.4)), existirá cierto grado de asociación entre ellas. Para evaluar dicho grado de asociación vamos a calcular el estadística $\chi^2$. Para ello, necesitamos calcular las frecuencias que teóricamente cabría esperar si las variables fuesen independientes. Estas frecuencias teóricas las calculamos a partir del teorema de caracterización (Ecuación 2.5), que debe cumplirse al suponer independientes las variables, de forma que: \[n^T_{ij}=\displaystyle \frac{n_{i\bullet}\cdot n_{\bullet j}}{n} \tag{2.23}\]

Comenzamos por la primera celda ($i=1,j=1$): \[n^T_{11}=\displaystyle \frac{n_{1\bullet}\cdot n_{\bullet 1}}{n}=\frac{1,896\cdot 1,300}{3,860} = 638.55\] Continuamos con la segunda celda ($i=1,j=2$): \[n^T_{12}=\displaystyle \frac{n_{1\bullet}\cdot n_{\bullet 2}}{n}=\frac{1,896\cdot 1,512}{3,860} = 742.68\] y así sucesivamente calcularíamos las frecuencias conjuntas teóricas del resto de la tabla de contingencia. Esta información se recoge en la siguiente tabla:

Tabla 2.26: Tabla contingencia: frecuencias teóricas (supuesto: sexo y efectos mas preocupantes COVID-19 independientes).

Sexo/Efecto	Salud	Economía	Ambos	Ninguno	No sabe	No contesta
Hombre	638.5492	742.6819	498.0684	10.3150	3.9295	2.4560
Mujer	661.4508	769.3181	515.9316	10.6850	4.0105	2.5440

Una vez disponemos de las frecuencias observadas y las frecuencia teóricas, calculamos la suma de los cuadrados de las discrepancias relativas entre cada para de ellos:

\[\chi^2 = \displaystyle \sum_{i=1}^{I=2} \sum_{j=1}^{J=7} \frac{(n_{ij}-n^T_{ij})^2}{n^T_{ij}}=\frac{(n_{11}-n^T_{11})^2}{n^T_{11}}+\frac{(n_{12}-n^T_{12})^2}{n^T_{12}} +...+\frac{(n_{17}-n^T_{17})^2}{n^T_{17}}+\] \[+\frac{(n_{21}-n^T_{21})^2}{n^T_{21}}+\frac{(n_{22}-n^T_{22})^2}{n^T_{22}}+...+\frac{(n_{27}-n^T_{27})^2}{n^T_{27}}\]

Sustituyendo los valores: \[\chi^2 = \displaystyle\frac{(636-638.5492)^2}{638.5492}+\frac{(840-742.6819)^2}{742.6819}+...+\frac{(0-2.5440)^2}{2.5440}\] \[\chi^2 \approx 72.517\] Como el valor del estadístico es distinto de 0 constatamos la existencia de asociación entre las variables objeto de estudio, algo que por otra parte ya sabíamos gracias al teorema de caracterización de independencia.

Como el estadístico $\chi^2$ no está acotado superiormente no podemos determinar cómo de intensa es la asociación.

2.7.2 Coeficiente de contingencia $C$ de Pearson

Este coeficiente se basa en el coeficiente de contingencia $\chi^2$, y está recomendado para muestras grandes. Esta medida se calcula a través de la siguiente expresión:\[C = \sqrt {\displaystyle \frac{\chi^2}{\chi^2 + n}} \tag{2.24}\] El coeficiente C está acotado, de forma que: \[0 \leq C < 1\] Obsérvese que $C$ no llega a tomar el valor 1, incluso en el supuesto de que la asociación entre las variables fuese perfecta; este es el principal inconveniente de esta medida. Por el contrario, si $C=0$, entonces las variables son independientes. Así pues, cuanto más se aproxime el valor del coeficiente $C$ a cero, menor será el grado de asociación entre las variables; y cuanto mas se aproxime el valor a 1, mayor será el grado de asociación entre los atributos.

2.7.3 Coeficiente de contingencia $V$ de Cramer

El coeficiente de contingencia V es adecuado para comparar el grado de asociación presente en diversas tablas de contingencia, especialmente cuando los tamaños (muestrales o poblacionales) son distintos. El coeficiente V de Cramer se calcula como: \[V = \sqrt {\displaystyle \frac{\chi^2}{n\cdot (k-1)}} \tag{2.25}\] donde $k$ es el valor mínimo entre el número de filas ($I$) y el número de columnas ($J$) de la tabla de contingencia.

El valor $V$ se encuentra acotado, tal que: \[0 \leq V \leq 1\] Si $V=0$, las variables son independientes; si $V=1$, existe una asociación perfecta entre las variables.

Ejemplo 2.14 En el Ejemplo 2.13 obtuvimos el valor del coeficiente de contingencia $\chi^2=72.517$ y constatamos la existencia de asociación entre las variables P2 y SEXO. Sin embargo, como el coeficiente $\chi^2$ no está acotado superiormente no podíamos decir nada sobre el grado de dicha asociación.

Como el tamaño de la muestra es grande ($n=3,860$), vamos a calcular el coeficiente de contingencia $C$ de Pearson que mide la asociación en el intervalo de 0 a 1.

Solución: Sustituyendo en la Ecuación 2.24 obtenemos el valor del coeficiente C: \[C=\sqrt{\frac{72.517}{72.517+3,860}}=0.1358\] El valor del coeficiente $C$ está mucho más próximo a 0 que a 1, esto indica que el grado de asociación entre las variables P2 (efectos mas preocupantes de la COVID-19) Y SEXO no es realmente muy elevado.

El coeficiente $V$ de Cramer será: \[V=\sqrt{\frac{72.517}{3,860 \cdot (2-1)}}=0.1371\] donde k= 2 porque es el mínimo entre el número de filas ($I=2$) y el número de columnas ($j=7$).

El valor $V=0.1371$ indica una asociación bastante débil entre las variables consideradas.

2.7.4 Concordancia o correlación ordinal

Si las dos variables son de tipo ordinal y queremos estudiar el grado de asociación entre ellas, debemos medir el grado de concordancia o correlación ordinal.

La correlación ordinal trata de observar si los rangos (ordenación) de las variables se mueven en el mismo sentido o en sentido inverso y determinar el grado o intensidad de asociación entre ambas variables ordinales. Para ello, pueden utilizarse una serie de coeficientes específicos, entre los que cabe mencionar el coeficiente de correlación ordinal de Spearman, el coeficiente $\tau$ de kendall y el coeficiente $\gamma$ de Goodman y Kruskal.

Nos centramos en el coeficiente de correlación de Spearman. Para calcularlo, se sustituyen cada una de las modalidades de cada atributo por un número natural, ordenados de 1 a n (o N) en orden ascendente, y se calculan las diferencias de rangos entre las dos ordenaciones para cada uno de los individuos de la muestra (o de la población).

Si no hay empates en los rangos, puede calcularse el coeficiente de correlación ordinal de Spearman ($r_S$) a partir de las diferencias en las ordenaciones según la expresión: \[r_S= 1-6\cdot\begin{bmatrix} \displaystyle \frac{\displaystyle\sum_{i=1}^n d^2_i}{n^3-n} \end{bmatrix} \tag{2.26}\] donde $d_i$ es la diferencia entre los rangos asignados al caso $i$ en cada una de las ordenaciones.

En el supuesto de que se produzcan empates en las ordenaciones, puede optarse por: (1) asignar a la categoría el rango medio obtenido o como recomiendan algunos autores; (2) aplicar el coeficiente de correlación de Pearson (Ecuación 2.16)) sobre las variables ordenadas ($R_X$,$R_Y$), de forma que el coeficiente de correlación de rangos de Spearman se obtendría como sigue: \[r_{S}=\frac{S_{{R_X}{R_Y}}}{S_{R_X} \cdot {S_{R_Y}}} \tag{2.27}\] El coeficiente de correlación de Spearman se encuentra acotado: \[-1 \leq r_S \leq 1\] de manera que si $r_S=1$, los casos observados tienen los mismos rangos en ambas ordenaciones y, por tanto, existe concordancia perfecta entre las dos ordenaciones; por el contrario, si $r_S=-1$, la ordenación es exactamente la inversa para cada caso en las dos variables y, por tanto, existe discordancia perfecta entre las dos variables. Existirá ausencia de correlación ordinal o concordancia entre las dos ordenaciones cuando $r_S=0$.

Cuando $0 < r_S < 1$, existe cierto grado de concordancia entre las dos ordenaciones, es decir, varían en el mismo sentido; la concordancia será más débil cuando más próximo a 0 se encuentre el valor de coeficiente.

Cuando $-1 < r_S < 0$, existe un cierto grado de discordancia, las variables varían en sentido contrario, siendo más débil la relación cuanto más próximo a 0 se encuentre el valor del coeficiente.

En general, suele interpretarse la intensidad de la asociación como se muestra a continuación:

Tabla 2.27: Interpretación general del valor del coeficiente de correlación de Spearman.

$0<\|r_S\| \leq 0.19$	Muy débil
$0.20\leq\|r_S\| \leq 0.39$	Débil
$0.40\leq\|r_S\|\leq 0.59$	Moderada
$0.60\leq\|r_S\| \leq 0.79$	Fuerte
$0.8\leq\|r_S\|<1$	Muy fuerte

Ejemplo 2.15 El siguiente conjunto de datos muestra la relación entre la producción de una empresa y el salario de sus empleados durante 5 años.

Tabla 2.28: Spearman a partir de variables numéricas.

Producción	1,000	2,000	2,500	4,000	2,300
Salarios	150	200	250	700	180

Calcula la correlación de Spearman entre producción y salarios.

Solución: Para calcular el coeficiente de correlación de Spearman, lo primero que hacemos es asignar los rangos a las variables. Esto lo hacemos en las filas 3 y 4. Una vez tenemos los rangos, calculamos la diferencia de rangos ($d$) y la diferencia al cuadrado ($d^2$), como se recoge en las filas 5 y 6 respectivamente.

Tabla 2.29: Spearman a partir de variables numéricas. Cálculos intermedios.

Producción	1,000	2,000	2,500	4,000	2,300
Salarios	150	200	250	700	180
Rango producción	5	4	2	1	3
Rango Salarios	5	3	2	1	4
$d$	0	1	0	0	-1
$d^2$	0	1	0	0	1

Por tanto, aplicando la expresión dada en la ecuación: \[r_S= 1-6\cdot\begin{bmatrix} \frac{\displaystyle\sum_{i=1}^{n=5} d^2_i}{n^3-n} \end{bmatrix}=1-6\cdot \displaystyle \frac{0+1+0+0+1}{5^3-5}=1-6\cdot\frac{2}{120}=0.9\]

El resultado obtenido indica que la asociación entre producción y salarios de la empresa considerada es positiva y muy fuerte.

Ejemplo 2.16. con Excel. En Excel podemos resolver el Ejemplo 2.15 porque las ordenaciones de los valores no se repiten, no tenemos empates. Para ello, lo primero que tenemos que hacer es ordenar los valores de las variables, lo hacemos con la función JERARQUIA.MEDIA(), y a continuación calcularemos la correlaciones entre dichas ordenaciones con la conocida función COEF.DE.CORRELACION().

La función JERARQUIA.MEDIA() tiene 3 argumentos. El primero se refiere al valor que se ordena; el segundo al rango de referencia en la ordenación; y el tercero es para especificar si la ordenación es descendente (valor 0) o ascendente (valor 1).

Reproducimos, por columna, los datos a los que se refiere el Ejemplo 2.15. En la celda C1 escribimos orden producción y en la celda D1 escribimos orden salarios. Seguidamente, en la celda C2 introducimos la fórmula: =jerarquia.media(A2;$A$2:$A$6;1), y análogamente en la celda D2: =jerarquia.media(B2:$B$2:$B$6;1). Arrastramos el rango C2:D2 hacia abajo hasta la fila 6 para copiar las fórmulas.

Una vez tenemos las ordenaciones, calculamos la correlaciones entre ellas. En la celda A8 escribimos Spearman y realiamos en cálculo en la celda B8 introduciendo la fórmula: =coef.de.correlacion(C2:C6;D2:D6). El resultado, la correlación de Sperman entre la producción y el salario es 0.9, una correlación alta y positiva. La hoja de cálculo en la que hemos trabajado debe ser similar a la que se reproduce en la Figura 2.17.

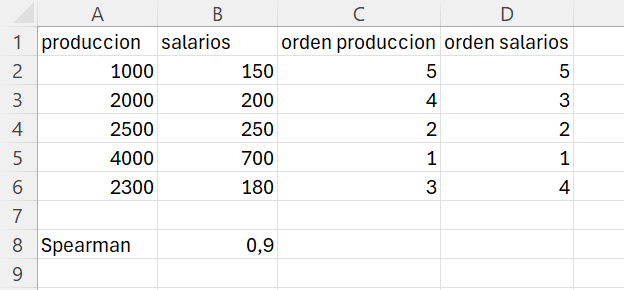
Figura 2.17: Correlación de Spearman con Excel.

Guardar el fichero con el nombre ej-2-16.

En la animación que encontrarás en [https://www.uv.es/ticstat/ej_2_16.gif](https://www.uv.es/ticstat/ej_2_16.gif) puedes ver cómo se ha resuelto este ejemplo para calcular el coeficiente de correlación de Spearman.

Ejemplo 2.16 A partir de la información proporcionada en la Tabla 2.30, calcula el coeficiente de correlación de Spearman entre las variables X e Y.

Tabla 2.30: Spearman a partir de variables categóricas.

X	Bueno	Excelente	Bueno	Excelente	Excelente	Excelente
Y	Malo	Bueno	Malo	Excelente	Muy Bueno	Bueno

Solución: En este ejemplo tenemos que tanto la variable X como la variable Y presentan categorías que se repiten, lo que al proceder a la ordenación da lugar a empates. Consideremos por ejemplo la variable X en la categoría Excelente se repite 4 veces; al asignar el rango a esta categoría le asignaríamos los rangos: 1, 2, 3 y 4 (ver fila 3 en la Tabla 2.31). Por tanto, su rango medio sería 2.5 (fila 5). De la misma forma procederíamos con el resto de casos. Las ordenanaciones y sus diferencias se muestran en la Tabla 2.31.

Tabla 2.31: Spearman a partir de variables categóricas. Cálculos intermedios.

X	Bueno	Excelente	Bueno	Excelente	Excelente	Excelente
Y	Malo	Bueno	Malo	Excelente	Muy Bueno	Bueno
Rango X	5 a 6	1 a 4	5 a 6	1 a 4	1 a 4	1 a 4
Rango Y	5 a 6	3 a 4	5 a 6	1	2	3 a 4
Rango medio X	5.5	2.5	5.5	2.5	2.5	2.5
Rango medio Y	5.5	3.5	5.5	1	2	3.5
$d$	0	-1	0	1.5	0.5	-1
$d^2$	0	1	0	2.25	0.25	1

Nuevamente, aplicando la Ecuación 2.26: \[r_S= 1-6\cdot\begin{bmatrix} \frac{\displaystyle\sum_{i=1}^{n=6} d^2_i}{n^3-n} \end{bmatrix}=1-6\cdot \displaystyle \frac{0+1+0+2.25+0.25+1}{6^3-6}\] \[r_S=1-6\cdot\frac{27}{210}\approx0.8714\] En consecuencia, podemos decir que la asociación entre las variables X e Y es positiva y muy fuerte.

2.8 Ejercicios

Ejercicio 2.1 En un período de 5 años, se observaron los valores de la variación anual en la tasa de desempleo (variable X) y la variación anual en la tasa media de absentismo laboral por enfermedad (variable Y) que se muestran en la siguiente tabla.

X	Y
0.7	-0.1
2.9	-0.8
-0.8	0.2
-0.7	0.2
-1	0.2

Calcula la covarianza e interpreta el resultado obtenido en el contexto del problema.

Ejercicio 2.2 En una planta industrial se ha observado que el número de accidentes laborales podría estar relacionado con el número de horas de trabajo semanales. Durante un mes se ha monitoreado una muestra de 25 empleados en diferentes turnos. Se registraron las horas de trabajo semanales de cada empleado, tomando en cuenta el control de asistencia de la empresa y se documentaron todos los incidentes reportados en el mismo mes a través del sistema de salud y seguridad ocupacional de la empresa. Cada accidente registrado se relacionó con el empleado afectado. Los datos (simulados) registrados se encuentran disponibles en www.uv.es/ticstat/ejercicio_2_2.xlsx. Dibuja un diagrama de expresión y coméntalo. Calcula e interpreta, de forma completa, la posible relación lineal entre las variables. Practica el cálculo a mano y verifica los resutlados con Excel.

(Nota: Este ejercicio se propuso en un examen una prueba grado de Turismo de la Facultad de Economía de Valencia.)

Ejercicio 2.3 Construye una tabla de doble entrada con los datos a los que se refiere el Ejercicio 2.2.

¿Cuántos distintos valores toma la variable Horas semanales de trabajo?¿Y la variable Número de accidentes laborales?
Calcula el número medio de horas semanales trabajadas por los empleados que no registraron incidentes en el último mes.
Los empleados que comunicaron 3 o más incidentes, ¿cuántas horas semanales trabajaron por término medio?
¿Cuántas horas semanales de trabajo son superadas por el 20% de los empleados?
¿Cuantos accidentes laborales fueron comunicados durante el último mes por aproximadamente la mitad de los trabajadores?

Ejercicio 2.4 Se ha preguntado a los/las responsable de la concejalía de turismo de n municipios de la Comunidad Valenciana la importancia que tiene el turismo en su desarrollo socioeconómico y cuál es su producto turístico referente. Los resultados se exponen en la siguiente tabla:

Tabla de datos del Ejercicio 2.4
Importancia	Sol y playa	Turismo rural	`\|`	$n_{i\bullet}$
El turismo es la principal actividad económica	35	?	`\|`	51
El turismo tiene un peso destacado	10	10	`\|`	?
El turismo es una actividad residual	?	4	`\|`	19
—	—	—	—	—
$n_{\bullet j}$	60	30	`\|`	?

Obtén justificadamente los 4 datos que faltan en la tabla.
A partir de estos datos, ¿qué coeficiente o coeficientes podemos utilizar para averiguar si hay asociación entre la “importancia del turismo en el desarrollo socioeconómico” y el “producto turístico referente”, sabiendo que el estadístico ji-cuadrado de Pearson $\chi^2$ es de 3.87? Calcula y justifica la respuesta.
A partir de los resultados obtenidos en el apartado anterior, valora el grado de asociación existente entre las dos características “importancia del turismo en el desarrollo socioeconómico” y “producto turístico referente”.

(Nota: Este ejercicio se propuso en una prueba del grado de Turismo de la Facultad de Economía de Valencia.)

Ejercicio 2.5 Para una muestra de 50 empleados de distintos departamentos de una gran multinacional, se ha registrado su edad, en base a los expedientes de RRHH, y el número de lesiones por sobreesfuerzo que figuran en los informes de salud laboral que se presentaron el último año. Los datos (simulados) se encuentran disponibles en www.uv.es/ticstat/ejercicio_2_5.xlsx. Dibuja un diagrama de expresión y coméntalo. Calcula e interpreta, de forma completa, la posible relación lineal entre las variables. Practica el cálculo a mano y verifica los resutlados con Excel.

Ejercicio 2.6 En la siguiente tabla se recogen las ordenaciones (de mejor a peor) de las puntuaciones asignadas por un grupo de turistas que se alojan en glamping según su grado de preferencia por algunas de las características de esta estructura

Tabla de datos del Ejercicio 2.6
Características del glamping	Españoles	Resto Europa
Uso energías renovables	2	1
Gestión sostenible de residuos	1	2
Gestión sostenible de recursos hídricos	4	3
Uso de recursos naturales para su construcción	3	4

Calcula un coeficiente adecuado, justificando su elección, para valorar el grado de relación entre la opinión de los turistas nacionales y de resto de europeos, sobre su preferencia por alguna de las características asociadas al alojamiento glamping. Interpreta el resultado obtenido.

(Nota: Este ejercicio se propuso en una prueba del grado de Turismo de la Facultad de Economía de Valencia.)

Ejercicio 2.7 Sea la variable estadística bidimensional (X, Y) con la siguiente distribución de frecuencias conjunta:

X/Y	100	150
0	1	2
1	2	4

Además, el valor de las medias y varianzas de las distribuciones marginales son:

\[\overline{x}=0.67 \qquad S^2_X=0.22 \qquad \overline{y}=133.33 \qquad S^2_Y=555.56\]

A partir de la información anterior, contesta las siguientes cuestiones justificando tus respuestas:

¿Son estadísticamente independientes las variables X e Y?
¿Cuál debe ser el valor de la covarianza?

Ejercicio 2.8 El ayuntamiento de un municipio está analizando diversos aspectos sobre los establecimientos hosteleros ubicados en el mismo. Observando de forma conjunta el número de mesas que cada establecimiento saca a la terraza (X) y los ingresos diarios, en euros, recaudados por este concepto (Y), se obtiene la siguiente distribución de frecuencias:

Tabla de datos del Ejercicio 2.8
X/Y	100	200	300
4	6	3	0
6	2	1	1
8	2	3	2
10	0	1	2

Comprueba, a través de las frecuencias, la dependencia de las dos características estudiadas.
Calcula la media y la varianza de los ingresos de los establecimientos que sacan ocho mesas a la terraza.
¿Cuál de las dos variables observadas presenta mayor regularidad? Razona la respuesta.

Ejercicio 2.9 ¿Cuál de las siguientes matrices puede ser una matriz de varianzas-covarianzas de una variable bidimensional (X, Y)? Razonad la respuesta. \[(a) \begin{pmatrix} 1 &1 \\ 1 & -2 \end{pmatrix} \qquad (b) \begin{pmatrix} 5 &2 \\ 1 & 5 \end{pmatrix} \qquad (c) \begin{pmatrix} 2.5 &4 \\ 4 & 3.3 \end{pmatrix} \qquad (d) \begin{pmatrix} 1 &1 \\ 1 & 2 \end{pmatrix}\]

Ejercicio 2.10 Una empresa de consultoría y formación desea evaluar si los cursos de capacitación en seguridad laboral tienen un impacto en la reducción de accidentes. Para ello, ha recopilado datos de una muestra de 100 trabajadores del sector de la construcción. En estos datos se incluye el número de cursos de seguridad completados por cada trabajador y el índice de accidentes por cada 100 empleados en las empresas donde trabajan. Los datos (simulados) se encuentran disponibles en www.uv.es/ticstat/ejercicio_2_10.xlsx. Dibuja un diagrama de dispersión y coméntalo. Calcula e interpreta, de forma completa, la posible relación lineal entre las variables. Practica el cálculo a mano y verifica los resutlados con Excel.

X`\`Y	\(y_1\)	\(y_2\)	\(\cdots\)	\(y_j\)	\(\cdots\)	\(y_J\)
\(x_1\)	\(n_{11}\)	\(n_{12}\)	\(\cdots\)	\(n_{1j}\)	\(\cdots\)	\(n_{1J}\)
\(x_2\)	\(n_{21}\)	\(n_{22}\)	\(\cdots\)	\(n_{2j}\)	\(\cdots\)	\(n_{2J}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(x_i\)	\(n_{i1}\)	\(n_{i2}\)	\(\cdots\)	\(n_{ij}\)	\(\cdots\)	\(n_{iJ}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(x_I\)	\(n_{I1}\)	\(n_{I2}\)	\(\cdots\)	\(n_{Ij}\)	\(\cdots\)	\(n_{IJ}\)

X`\`Y	\(y_1=1,200\)	\(y_2=1,300\)	\(y_3=1,400\)
\(x_1=2\)	\(n_{11}=4\)	\(n_{12}=1\)	\(n_{13}=0\)
\(x_2=3\)	\(n_{21}=1\)	\(n_{22}=3\)	\(n_{23}=0\)
\(x_3=4\)	\(n_{31}=0\)	\(n_{32}=1\)	\(n_{33}=5\)

X`\`Y	\(y_1\)	\(y_2\)	\(\cdots\)	\(y_j\)	\(\cdots\)	\(y_J\)	\(n_{i\bullet}\)
\(x_1\)	\(n_{11}\)	\(n_{12}\)	\(\cdots\)	\(n_{1j}\)	\(\cdots\)	\(n_{1J}\)	\(n_{1\bullet}\)
\(x_2\)	\(n_{21}\)	\(n_{22}\)	\(\cdots\)	\(n_{2j}\)	\(\cdots\)	\(n_{2J}\)	\(n_{2\bullet}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(x_i\)	\(n_{i1}\)	\(n_{i2}\)	\(\cdots\)	\(n_{ij}\)	\(\cdots\)	\(n_{iJ}\)	\(n_{i\bullet}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(x_I\)	\(n_{I1}\)	\(n_{I2}\)	\(\cdots\)	\(n_{Ij}\)	\(\cdots\)	\(n_{IJ}\)	\(n_{I\bullet}\)
\(n_{\bullet j}\)	\(n_{\bullet1}\)	\(n_{\bullet2}\)	\(\cdots\)	\(n_{\bullet j}\)	\(\cdots\)	\(n_{\bullet J}\)	\(n\)

X`\`Y	\(y_1=1,200\)	\(y_2=1,300\)	\(y_3=1,400\)	\(n_{i\bullet}\)
\(x_1=2\)	\(n_{11}=4\)	\(n_{12}=1\)	\(n_{13}=0\)	\(n_{1\bullet}=5\)
\(x_2=3\)	\(n_{21}=1\)	\(n_{22}=3\)	\(n_{23}=0\)	\(n_{2\bullet}=4\)
\(x_3=4\)	\(n_{31}=0\)	\(n_{32}=1\)	\(n_{33}=5\)	\(n_{3\bullet}=6\)
\(n_{\bullet j}\)	\(n_{\bullet1}=5\)	\(n_{\bullet2}=5\)	\(n_{\bullet3}=5\)	\(n=15\)

X`\`Y	\(y_1\)	\(y_2\)	\(\cdots\)	\(y_j\)	\(\cdots\)	\(y_J\)	`\|`	\(f_{i\bullet}\)
\(x_1\)	\(f_{11}\)	\(f_{12}\)	\(\cdots\)	\(f_{1j}\)	\(\cdots\)	\(f_{1J}\)	`\|`	\(f_{1\bullet}\)
\(x_2\)	\(f_{21}\)	\(f_{22}\)	\(\cdots\)	\(f_{2j}\)	\(\cdots\)	\(f_{2J}\)	`\|`	\(f_{2\bullet}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	`\|`	\(\vdots\)
\(x_i\)	\(f_{i1}\)	\(f_{i2}\)	\(\cdots\)	\(f_{ij}\)	\(\cdots\)	\(f_{iJ}\)	`\|`	\(f_{i\bullet}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	`\|`	\(\vdots\)
\(x_I\)	\(f_{I1}\)	\(n_{I2}\)	\(\cdots\)	\(f_{Ij}\)	\(\cdots\)	\(f_{IJ}\)	`\|`	\(f_{I\bullet}\)
—	—	—	—	—	—	—	—	—
\(f_{\bullet j}\)	\(f_{\bullet1}\)	\(f_{\bullet2}\)	\(\cdots\)	\(f_{\bullet j}\)	\(\cdots\)	\(f_{\bullet J}\)	`\|`	\(1\)

2 Análisis de datos de dos variables

2.1 Introducción.

2.2 Distribuciones de frecuencias bidimensionales.

2.2.1 Distribución de frecuencias conjuntas y marginales.

2.2.2 Distribuciones de frecuencias condicionadas

2.3 Diagrama de dispersión.

2.3.1 Detección de valores anómalos

2.4 Independencia estadística

2.5 Covarianza.

2.5.1 Intepretación de la covarianza.

2.5.2 Matriz de varianzas-covarianzas

2.6 Teoría de la correlación

2.6.1 Interpretación del coeficiente de correlación

2.6.2 Matriz de correlación

2.7 Asociación y concordancia

2.7.1 Coeficiente de contingencia \(\chi^2\).

2.7.2 Coeficiente de contingencia \(C\) de Pearson

2.7.3 Coeficiente de contingencia \(V\) de Cramer

2.7.4 Concordancia o correlación ordinal

2.8 Ejercicios

X/Y	\(f_{i/j=1}\)
0	\(f_{11}=\displaystyle\frac{n_{11}}{n_{\bullet1}}=\frac{1}{3}\)
1	\(f_{21}=\displaystyle\frac{n_{21}}{n_{\bullet1}}=\frac{2}{3}\)

X/Y	\(f_{i/j=2}\)
0	\(f_{11}=\displaystyle\frac{n_{12}}{n_{\bullet2}}=\frac{2}{6}=1/3\)
1	\(f_{22}=\displaystyle\frac{n_{22}}{n_{\bullet2}}=\frac{4}{6}=2/3\)

Y/X	\(f_{j/i=1}\)
1	\(f_{11}=\displaystyle\frac{n_{11}}{n_{1\bullet}}=\frac{1}{3}\)
2	\(f_{12}=\displaystyle\frac{n_{12}}{n_{1\bullet}}=\frac{2}{3}\)

Y/X	\(f_{j/i=2}\)
1	\(f_{21}=\displaystyle\frac{n_{21}}{n_{2\bullet}}=\frac{2}{6}=1/3\)
2	\(f_{22}=\displaystyle\frac{n_{22}}{n_{2\bullet}}=\frac{4}{6}=2/3\)