1 Análisis de datos de una variable

1.1 Introducción

Comenzamos la sección dedicada a introducir los fundamentos básicos de estadística descriptiva definiendo tres conceptos esenciales: Universo, Población y Muestra.

Universo: es el colectivo, conjunto de individuos o elementos (personas, hogares, empresas, países, etc.), objeto de estudio.
Población: es el conjunto de las posibles observaciones de la característica (o variable) común que queremos analizar de un universo. La población puede ser finita o infinita. Si únicamente consideramos las observaciones de una característica del universo obtendremos una población unidimensional; pero si consideramos dos variables tendremos una población bidimensional, si consideramos tres variables una población tridimensional, etc.

No obstante, muchos autores, investigadores e investigaciones no distinguen entre universo y población (Tang (1951); Kendall y Buckland (1957) y Poch (1969)).

Observad que el concepto de población en estadística no es el que utilizamos en el lenguaje cotidiano para referirnos a una población.

Ejemplo 1.1 Consideremos las siguientes definiciones de universo y población. Observad la diferencia.

Universo: Estudiantes de la Universidad de Valencia.
Población (unidimensional): Edades de los estudiantes de la Universidad de Valencia.
Población (tridimensional): Edades, grado que cursan y coste de la matrícula de los estudiantes de la Universidad de Valencia.

Muestra: Es una parte (un subconjunto) representativa de la población. En muchas situaciones no es posible acceder al estudio de la población por diversas razones: imposibilidad, coste, etc. Por esta razón utilizamos la muestra para obtener información relevante acerca de la población.

Ejemplo 1.2 El fichero FT3351.pdf (descárgalo aquí) corresponde a la ficha técnica del Barómetro de febrero de 2022 del CIS. De acuerdo con la ficha técnica, el universo del estudio es la población española de 18 años o más. El tamaño de la muestra es de 4,000 individuos.

Ejemplo 1.3 En la Encuesta Sobre Estrategias Empresariales (ESEE), elaborada por la Fundación SEPI (https://go.uv.es/9Hcqmsn), la población de referencia son las empresas con 10 o más trabajadores de lo que se conoce habitualmente como industria manufacturera. El tamaño de la muestra ha ido cambiando del año 1991 (cuando se inicia esta encuesta) hasta el año 2017 (último año en que se realizó). En 2017 el tamaño de la muestra fue de 5,840 empresas.

En los ejemplos 1.1 y 1.3 se define el universo, colectivo objeto de estudio de las investigaciones. La diferencia es que la investigación del CIS se refiere al término universo y la de la Fundación SEPI se refiere al término población (cuando realmente es el universo).

Ejemplo 1.4 Volviendo al Barómetro del CIS, el universo es la población española de 18 años o más. Este es el colectivo objeto de estudio. Sobre este colectivo interesa obtener respuesta sobre una serie de preguntas, que se recogen en el documento cues3351.pdf (descárgalo aquí). Las preguntas se codifican y se hacen corresponder con las características o variables objeto de estudio. La codificación de las variables y sus correspondientes valores/categorías se encuentran en el documento codigo3351.pdf. Si analizamos cada variable por separado estamos realizando un análisis unidimensional (o de una variables), si analizamos conjuntamente dos variables realizamos un análisis bidimensional (o de dos variables), etc.

En estadística, las medidas (media, varianza, etc.) que describen las características de una muestra se denominan estadísticos y se suelen representar con letras latinas:

media: $\bar{x}$
varianza: $S^2_X$
desviación típica: $S_X$
covarianza: $S_{XY}$
coeficiente de correlación: $r_{XY}$
etc.

En cambio, cuando estas mismas medidas hacen referencia a la descripción de características de la población se denominan parámetros y se representan con letras griegas:

media: $\mu_{x}$
varianza: $\sigma^2_{X}$
desviación típica: $\sigma_X$
covarianza: $\sigma_{XY}$
coeficiente de correlación: $\rho_{XY}$
etc.

En este manual, salvo que se indique lo contrario, nos referiremos a datos procedentes de una muestra.

1.2 Variables estadísticas y datos

En estadística utilizamos el término variable para referirnos a la característica que queremos analizar o investigar sobre un conjunto de individuos u observaciones.

Existen distintas formas de clasificar las variables en función de cómo se miden. Una clasificación muy extendida consiste en distinguir entre variables cuantitativas y variables cualitativas.

Las variables cuantitativas son aquellas en las que la característica que queremos estudiar puede cuantificarse, esto es, puede expresarse de forma numérica. A su vez, podemos hablar de:

variables discretas: Cuando el dominio de la variable es un conjunto numerable de valores. Suele hacer referencia a variables que suelen medirse mediante conteo. Por ejemplo: Número de hijos, número de miembros del hogar, número de personas que votan a un determinado partido político, número de piezas defectuosas, número de acciones negociadas del banco XYZ un día cualquiera, etc.
variables continuas: Cuando el dominio de la la variable es continuo y, por tanto, la variable puede tomar teóricamente cualquier valor en determinado intervalo infinitesimal. Este tipo de variables suele proceder de procesos de medición, y la precisión de la medición depende de la precisión del instrumento de medida. Por ejemplo: la edad, la altura, la temperatura, el precio de la gasolina, el salario de los trabajadores, etc.

Sin embargo, en muchas ocasiones variables continuas se presentan como variables discretas. Este es, por ejemplo, el caso de la edad. Cuando se pregunta a un inviduo por su edad no responde 35 años-8 meses-12 días, dice 35 años. ¿Qué quiero decir con esto?, que, en ocasiones, variables continuas tienden a considerarse como si fueran discretas; cuando se hace esto se dice que la variable se ha discretizado (es una variable continua discretizada).

En general, los valores monetarios son variables cuantitativas continuas. Consideremos el siguiente ejemplo. El salario suele expresarse con dos decimales (el trabajador cobra 1,780.74 €); el precio de la gasolina se expresa con tres decimales (el precio del litro de gasolina es 1.819 €); el precio de la luz se expresa con 5 decimales (el precio del kWh de luz por hora es de 0.15076); etc. Dependiendo de qué es lo que se mide se utiliza mayor o menor precisión en la medición.

Respecto a las variables cuantitativas, también es frecuente distinguir entre:

escala de intervalo: establece la distancia entre dos valores. En este tipo de escala existe el cero, pero es un valor arbitrario.
escala de razón: en este tipo de escala el cero tien sentido absoluto y representa la ausencia de la característica que mide.

Las variables cualitativas o atributos son aquellas cuyos valores son categorías, también denominadas modalidades. Podemos distinguir entre:

Variables nominales: Cuando las modalidades que toma la variable no se pueden ordenar. Por ejemplo: estado civil, profesión, provincia de residencia, etc.
Variables ordinales: Cuando existe una ordenación natural entre las distintas categorías que toma la característica (variable) estudiada. Por ejemplo: nivel de estudios, satisfacción de los clientes con el servicio prestado, etc.

Otra terminología frecuente en el ámbito de la estadística para referirnos a variables cualitativas es: si la variable solo toma dos categorías se denomina variable dicotómica, si toma más de dos categorías se denomina variable politómica.

Ejemplo 1.5 Identificar el tipo de las siguientes variables:

Número de miembros de la unidad familiar con ingresos.
Lugar de nacimiento.
Duración de una clase de estadística básica.
Nivel certificado de compentencia en inglés.
Número de libros vendidos en una librería a lo largo de una semana.
Experiencia laboral (en años).
Grado de satisfacción con el grado universitario estudiado.
Compañía con la que se tiene contratado un seguro médico.

Solución:

Cuantitativa discreta. Los miembros de la unidad familiar con ingresos pueden ser: 0, 1, 2,…
Variable nominal. El lugar de nacimiento puede tomar categoría como: Valencia, Alicante, Alzira, Cuenca, etc.
Variable continua. La precisión del tiempo que dura una clase dependerá del instrumento de medición, generalmente redondeamos y decimos: 1 hora y 30 minutos; pero en el intervalo 1h30min-1h31min, la variable puede tomar infinitos valores.
Variable ordinal. El grado de competencia en inglés tomará valores: A1, A2, B1, B2, C1, C2. Estas categorías tienen una ordenación. Por ejemplo, el nivel C1 es menor que el C2.
Variable discreta. El número de libros vendidos será: 0, 1, 2, 3,..,15,.,.20,…
Variable discreta. Aunque el tiempo es una variable continua, cuando hablamos de años de experiencia laboral estamos discretizando la característica. La variable esperamos que tome valores: 0, 1, 2,…
Variable ordinal. El grado de satifacción puede ser: muy satisfecho, satisfecho, indiferente, insatisfecho, muy insatisfecho. De nuevo, existe una ordenación en las categorías que toma la variable.
Variable nominal. El seguro médico lo podemos tener contratado con la compañía A, B, C,…

1.2.1 Metadatos y datos

Los metadatos son los datos de los datos, es una descripción completa de los datos con los que vamos a trabajar.

La información contenida en los metadatos puede variar ampliamente en términos de integridad, consistencia y precisión general.

Dado que los metadatos a menudo proporcionan gran parte de nuestra información preliminar sobre el contenido de un conjunto de datos, son extremadamente importantes y cualquier limitación de estos -incompletitud, inconsistencia y/o inexactitud- puede causar serios problemas en nuestro análisis posterior.

Cuando nos referimos al término datos estamos haciendo referencia al valor numérico o categoría que toma la variable (o característica) en cada uno de los individuos.

1.3 Distribución de frecuencias y tabla de frecuencias

En muchas ocasiones resulta útil organizar el conjunto de valores de una variable en una tabla, a la que se denomina tabla de frecuencias o tabla estadística. Con la construcción de una tabla de frecuencias pretendemos resumir los datos disponibles de una variable para hacernos una idea de cómo es su distribución (de frecuencias).

También podemos resumir la información contenida en un conjunto de datos a través de representaciones gráficas y de valores numéricos por medio del cálculo de las oportunas medidas estadísticas (media, varianza, etc.).

Cuando nos referimos a una distribución de frecuencias y/o una tabla de frecuencias suele utilizarse la siguiente notación:

$X$: Variable estadística. Las variables suelen representarse mediante letras mayúsculas (X, Y, K, etc.).
$x_i$: Son cada uno de los valores de la variable. Los valores que toma una variable se representan mediante la misma letra que la variable pero en minúsculas ($x_i$, $y_i$, $k_i$,etc.). Una determinada variable puede tomar $I$ distintos valores.
$n$: Número total de observaciones o tamaño de la muestra.
Frecuencia absoluta ordinaria, $n_i$: Número de veces que se repite cada valor $x_i$ de la variable.
Frecuencia absoluta acumulada, $N_i$: Número de veces que se repite un valor inferior o igual a $x_i$, es decir: \[N_i = n_1 + n_2 +...+ n_i=\sum_{i=1}^i n_i \tag{1.1}\]
Frecuencia relativa ordinaria, $f_i$: Proporción de veces que se repite cada valor $x_i$ de la variable. Es el cociente entre cada una de las frecuencias absolutas y el número total de observaciones, es decir: \[f_i=\frac{n_i}{n} \tag{1.2}\]
Frecuencia relativa acumulada, $F_i$: Proporción de veces que se repite un valor inferior o igual a $x_i$, es decir: \[F_i=f_1+f_2+...+f_i=\sum_{i=1}^i f_i \tag{1.3}\] o también \[F_i = \displaystyle\frac{N_i}{n} \tag{1.4}\]

Si estamos trabajando con una muestra, el número total de observaciones es el tamaño de la muestra y se denota por n.

Si estamos trabajando con la población, el número total de observaciones es el tamaño de la población y se denota por N.

Cuando nos referimos a la distribución de frecuencias hacemos referencia al par formado por los valores que toma la variable, ordenados de menor a mayor, y su correspondiente frecuencia (absoluta o relativa). Así, podemos hablar de:

la distribución de frecuencias absolutas de la variable X: ($x_i$ , $n_i$)
la distribución de frecuencias relativas de la variable X: ($x_i$ , $f_i$)

Una tabla de frecuencias es la representación tabular de la distribución de frecuencias. Para obtener la tabla de frecuencias absolutas, por ejemplo como la que se muestra en la Tabla 1.1, ordenamos los valores de la variable ($x_i$) de menor a mayor y, a continuación, contamos cuantas veces ($n_i$) se repite cada valor ($x_i$).

Tabla 1.1: Tabla de frecuencias (Distribución de frecuencias absolutas)

$x_i$	$n_i$
$x_i$	$n_i$
$x_1$	$n_1$
$x_2$	$n_2$
$\vdots$	$\vdots$
$x_i$	$n_i$
$\vdots$	$\vdots$
$x_I$	$n_I$

En lugar de las frecuencias absolutas podemos representar las frecuencias relativas en una tabla de frecuencias (Tabla 1.2). Para ello, ordenamos los valores de la variable $X$ de menor a mayor y calculamos el porcentaje (o tanto por uno) de veces ($f_i$) que se repite cada valor ($x_i$).

Tabla 1.2: Tabla de frecuencias (Distribución de frecuencias relativas)

$x_i$	$f_i$
$x_1$	$f_1$
$x_2$	$f_2$
$\vdots$	$\vdots$
$x_i$	$f_i$
$\vdots$	$\vdots$
$x_I$	$f_I$

Cuando construimos tablas de frecuencias y realizamos los cálculos a mano de la media, la mediana, la varianza, etc., es habitual que partamos de la Tabla 1.1) y le añadamos columnas para recoger los cálculos intermedios. De esta forma, si calculamos las frecuencias absolutas y relativas, tanto ordinarias como acumuladas, la tabla podría tener el aspecto que se muestra en la Tabla 1.3.

Tabla 1.3: Tabla con frecuencias absolutas y relativas

$x_i$	$n_i$	$N_i$	$f_i$	$F_i$
$x_1$	$n_1$	$N_1$	$f_1$	$F_1$
$x_2$	$n_2$	$N_2$	$f_2$	$F_2$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$x_i$	$n_i$	$N_i$	$f_i$	$F_i$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$x_I$	$n_I$	n	$f_I$	1
	———		———
	$\sum=n$		$\sum=1$

La tabla de frecuencias también puede utilizarse para resumir una variable cualitativa.

Ejemplo 1.6 Se ha seleccionado un total de 15 empleados de una empresa y se les ha preguntado por su experiencia en la empresa, en años (es otra forma de hablar de la antigüedad de los empleados). Los datos recopilados son:

1, 5, 2, 3, 3, 4, 5, 3, 2, 4, 3, 4, 2, 3, 4

Identificad la variable objeto de estudio y resumid la distribución de frecuencias de la variable en una tabla.

Solución: En primer lugar, la variable objeto de estudio es X=“experiencia en la empresa de los empleados (en años)”. Tenemos un total de 15 observaciones ($n=15$). Las observaciones (o individuos) son cada uno de los empleados seleccionados de la empresa.

La variable $X$ (experiencia en la empresa) toma 5 valores distintos ($I=5$), que son: $x_i=\left\{ 1,2,3,4,5 \right\}$.

Para construir la tabla de frecuencias ordenamos los valores de la variable de menor a mayor (columna 1) y contamos el número de empleados ($n_i$) a los que corresponde cada valor $x_i$ (columna 2). Si lo consideramos oportuno, añadimos columnas para calcular $N_i$ (columna 3), $f_i$ (columna 4) y $F_i$ (columna 5). Las frecuencias relativas se han expresado en tanto por uno.

Tabla 1.4: Tabla de frecuencias del ejemplo 1.6.

$x_i$	$n_i$	$N_i$	$f_i$	$F_i$
1	1	1	0.067	0.067
2	3	4	0.2	0.267
3	5	9	0.333	0.6
4	4	13	0.267	0.867
5	2	15	0.133	1
	————		———
	$\sum n=15$		$\sum=1$

Algunas interpretaciones de los resultados obtenidos:

$n_3=5$: 5 empleados tienen una experiencia en la empresa de 3 años.
$N_2=4$: 4 empleados tienen una experiencia en la empresa de 2 o menos años (hay 3 empleados con una experiencia de 2 años y 1 empleado con una experiencia de 1 año).
$f_3=0.333$: el 33.3% de los empleados tienen una experiencia en la empresa de 3 o menos años, también puede decirse que tienen una experiencia de como mucho 3 años.
$F_4=0.867$: el 86.7% de los empleados tienen un experiencia de como mucho 4 años. Por tanto, únicamente el 13.3% de los empleados tienen más de 4 años.

También podemos resumir los datos de una variable en forma gráfica. Los diagramas de barras o columnas se utilizan tanto si la variable es categórica (nominal u ordinal) como si es cuantitativa discreta.

Para construir un gráfico de barras/columnas situamos en el eje de abcisas (eje X) los valores o categorías que toma la variable y en el eje de ordenadas (eje Y) las frecuencias absolutas ($n_i$) o relativas ($f_i$). Sobre cada valor/categoría se construye una barra cuya altura es proporcional a su frecuencia.

Si la variable discreta toma muchos valores distintos, los formatos de la Tabla 1.1, Tabla 1.2 o Tabla 1.3 no serán válidos porque la tabla será muy larga. En estos casos es conveniente agrupar los valores de la variable en intervalos. Este tipo de distribución recibe el nombre de distribución de valores agrupados en intervalos.

En este tipo de distribución de frecuencias la notación que se utiliza es:

Los intervalos en los que agrupamos los datos los representamos por: $L_{i-1} , L_{i}$. Suponemos que los intervalos son cerrados por la izquierda y abiertos por la derecha, a excepción del último intervalo que también será cerrado por la derecha
Los conceptos de frecuencias son equivalentes. Esto es, $n_i$ será el número de observaciones que quedan incluidas en el intervalo i-ésimo, $N_i$ es el número de observaciones incluidas en el intervalo i-ésimo o anteriores, etc.

Una tabla de frecuencias para representar una distribución de frecuencias de valores agrupados puede ser la que se recoge en la Tabla 1.5.

Tabla 1.5: Tabla con frecuencias absolutas y relativas de valores agrupados.

$L_{i-1},L_i$	$n_i$	$N_i$	$f_i$	$F_i$
$[L_0,L_1[$	$n_1$	$N_1$	$f_1$	$F_1$
$[L_1,L_2[$	$n_2$	$N_2$	$f_2$	$F_2$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$[L_{i-1},L_i[$	$n_i$	$N_i$	$f_i$	$F_i$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$[L_{I-1},L_I]$	$n_I$	n	$f_I$	1
	———	——
	$\sum=n$	$\sum=1$

Para construir una tabla de frecuencias de valores agrupados en intervalos es necesario establecer el número de intervalos y su amplitud. Para hacerlo existen distintas alternativas, uno de estos procedimientos es el que se describe a continuación.

Paso 1.- Establecemos el número de intervalos: El número de intervalos, que se denota por K, en los que agrupar las observaciones puede obtenerse mediante diferentes criterios, por ejemplo:
- Fórmula de Sturges, que se suele utilizar cuando el número de observaciones es muy grande: Número de intervalos (K) = $\frac{log{\hspace{1mm}n}}{log\hspace{1mm}2}+1$
- Aproximar el número de intervalos K por la raiz cuadadrada del número de observaciones: $K=\sqrt{n}$
Paso 2.- Determinamos el recorrido de la variable, se obtiene por diferencia entre el mayor y menor valor que toma.
Paso 3.- Calculamos la amplitud que tendrán los intervalos. Para ello dividimos el recorrido por el número de intervalos.
Paso 4.- Construimos los K intervalos. El límite inferior del primer intervalo podemos identificarlo con el mínimo de la variable y a partir de ahí obtener el resto de intervalos sumándole la amplitud. Comprobamos que el último intervalo contiene el máximo de la variable.
Paso 5.- Contamos cuantas observaciones caen dentro de cada intervalo. Suele considerarse que los intervalos son abiertos (no incluye el valor) por la izquierda y cerrados por la derecha (incluye el valor), salvo el primer intervalo que será cerrado por la izquierda para contener al mínimo.

Cuando trabajamos con distribuciones de frecuencias de valores agrupados es conveniente determinar la amplitud de cada intervalo ($a_i = L_i - L_{i-1}$) y un valor representativo del mismo, que es conocido como Marca de clase (sele denotarse por $x_i$), que se calcula como el punto medio del intervalo: $x_i = \frac{L_{i-1} + L_i}{2}$

Si disponemos de todos los datos individualizados, solo los agrupamos (numérica o gráficamente) para tener una idea de cómo es su distribución de frecuencias. Los cálculos de las oportunas medidas estadísticas se realizan utilizando los datos originales, de lo contrario estaríamos perdiendo mucha información.

1.3.1 Aplicación práctica 1 con Excel

Vamos a reproducir los datos del Ejemplo 1.6 en Excel y a obtener la tabla estadística o tabla de frecuencias. Recordemos que estamos estudiando la experiencia (en años) de una muestra de 15 empleados.

datos de experiencia: 1 , 5 , 2 , 3 , 3 , 4 , 5 , 3 , 2 , 4 , 3 , 4 , 2 , 3 , 4

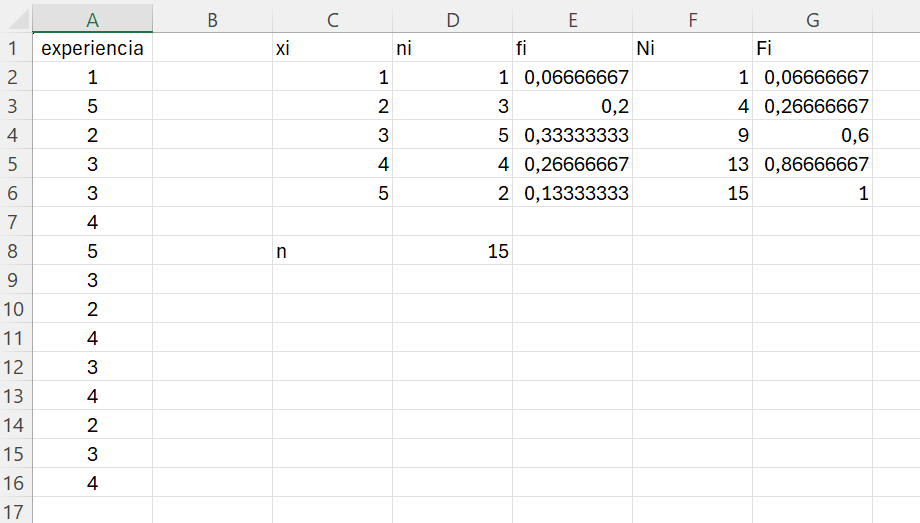
Abrimos Excel. En la celda A1 escribimos experiencia. A partir de la celda A2 introducimos los datos relativos a la experiencia; tendremos los datos en el rango A2:A16. Escribimos en la celda C1: xi; en la celda D1: ni; en la celda E1: fi; en la celda F1: Ni y en la celda G1: Fi. Para tener también el tamaño de la muestra escribimos en la C8: n.

Una vez tenemos los encabezados de la tabla, identificamos los valores únicos de experiencia en la columna C. Estos valores son: 1, 2, 3, 4 y 5.

Comenzando en la celda D2, marcamos el rango D2:D6 e insertamos la función FRECUENCIA(). Identificamos como datos el rango A2:A16, y como grupos el rango C2:C6, que se corresponde con los distintos valores que toma la experiencia.

Como la función FRECUENCIA() es una función matricial, para ejecutarla utilizaremos la siguiente combinación de teclas: CTRL+SHIFT+ENTER.

En este punto ya tenemos las dos primeras columnas de nuestra tabla de frecuencias. Las frecuencias relativas se obtienen al dividir las frecuencias ordinarias ni entre el tamaño de la muestra n, que se encuentra en la celda D8 y cuyo valor fijamos escribiendo el símbolo $ delante de la letra de la celda, para fijar la columna, y también delante del número, para fijar la fila.

En la siguiente columna, columna F, calculamos las frecuencia acumuladas. Para calcular la columna Ni tenemos que acumular las frecuencias ni. Para ello, hacemos que el valor de la celda E2 sea el de la celda D2; para acumular, el valor de la celda E3 será el anterior D3 al que sumaremos el valor acumulado de la celda E2. Arrastramos la celda E3 hasta la celda E6 para copiar el contenido. Comprobamos que el acumulado total coincide con nuestra muestra ($n=15$).

Las frecuencias relativas acumuladas las calcularemos diviendo la frecuencia ordinaria acumulada entre el número de obervaciones: $n=15$. Para fijar el valor de la celda recuerda que escribimos la referencia de la columna de la celda entre el símbolo $, es decir, escribimos $D$8. Así, el valor de la celda G2 será igual a F2, y la celda G3 será la F3 mas la acumulada anterior G2.

El resultado final debería ser similar al que se muestra en la Figura 1.1.

Figura 1.1: Tabla de frecuencias en Excel.

Puedes seguir la explicación de cómo se ha obtenido la tabla estadística de esta práctica en: [https://www.uv.es/ticstat/tabla_excel.gif](https://www.uv.es/ticstat/tabla_excel.gif)

Ahora vamos a realizar un gráfico de columnas/barras.

Para Excel, si las barras son verticales el gráfico es de columnas, y si las barras son horizontales el gráfico es de barras.

Nos situamos en la celda I1 de nuestra hoja Excel. Hacemos clic en Insertar, luego en el botón (Insertar gráfico de columnas o de barras). Seguidamente, seleccionamos el primero de los gráficos, un gráfico de columnas básico.

Se abre una plantilla vacía de dibujo. Si hacemos clic en cualquier parte de esta plantilla, se abrirá el menú de Diseño de gráfico, debe ser similar al que se muestra en la Figura 1.2.

Figura 1.2: Opciones de diseño de gráfico

Hacemos clic en Seleccionar datos, se abrirá la siguiente ventana:

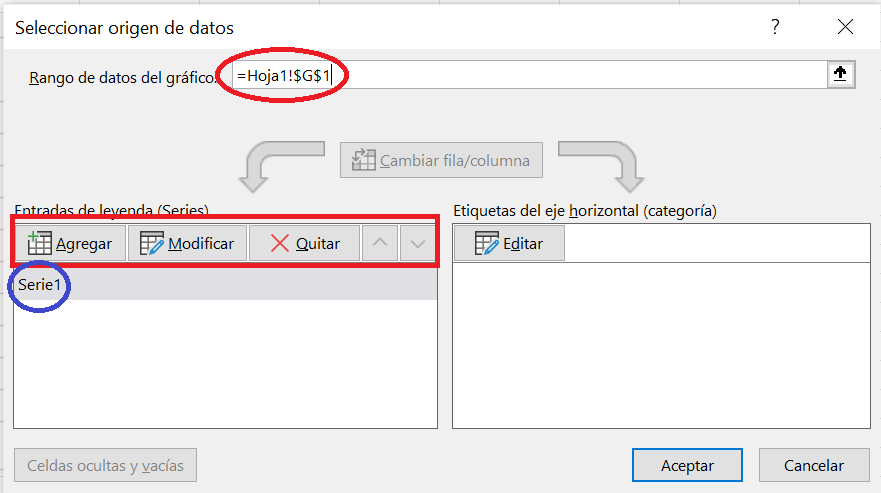
Figura 1.3: Ventana de selección de datos en gráfico.

Seleccionamos nuestro rango de datos (C2:C6). La serie de datos que hemos seleccionado aparece con el nombre por defecto de Series 1. Tenemos tres botones que sirven para: Agregar un nueva serie de dato; y Modificar o Quitar la serie de seleccionemos. Si hacemos clic en Modificar, se abre un cuadro que nos permite modificar tanto el nombre de la serie como el conjunto de datos. Cerranos este cuadro de dialogo, volvemos al cuadro de selección de rango de datos. En la caja de la derecha, que tiene como encabezado Etiquetas del eje horizontal (categorías), hacemos clic en el botón Editar. En el cuadro Rango de rótulos de eje seleccionamos el rango C2:C6.

Para crear el gráfico hacemos clic en Aceptar. Nuestro gráfico tendrá la siguiente apariencia.

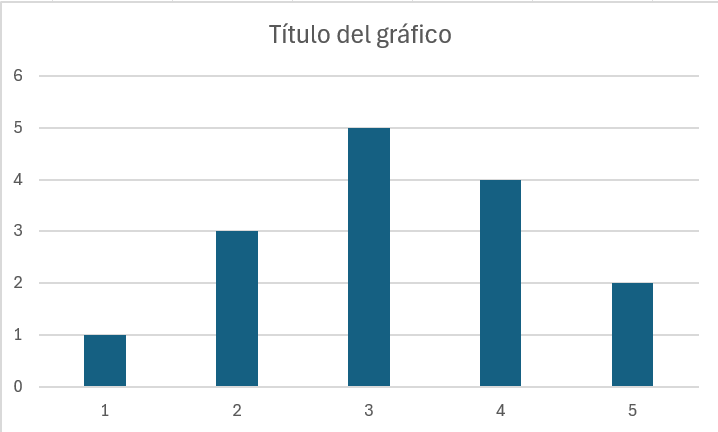
Vamos a mejorar el gráfico:

Hacemos clic sobre el gráfico. Aparecen tres botones en el lado derecho. Hacemos clic en el botón que abre el cuadro de Elementos de gráfico. Seleccionamos Titulos del eje. Observar el efecto que tiene sobre el gráfico las distintas opciones de selección. Cerramos los elementos de gráfico haciendo nuevamente clic sobre el botón . Editamos los títulos de los ejes y del gráfico haciendo doble clic sobre los cuadros de texto. En el eje X escribimos Años de experiencia, en el eje Y escribimos Número de empleados y como título principal del gráfico Distribución de la experiencia (n=15)
Clicamos sobre las barras del gráfico y, a continuación, clic en el botón derecho del ratón. Seleccionamos la opción Dar formato a serie de datos…. El primer botón se refiere a las opciones de relleno y borde. Clicamos sobre este botón y seleccionamos un color de relleno.

Dedicad un tiempo a investigar las distintas opciones de gráfico que se han comentado en la práctica: nombre de la serie, elementos de gráfico, relleno, borde, etc.

El resultado final debería ser similar al que se muestra en la Figura 1.5.

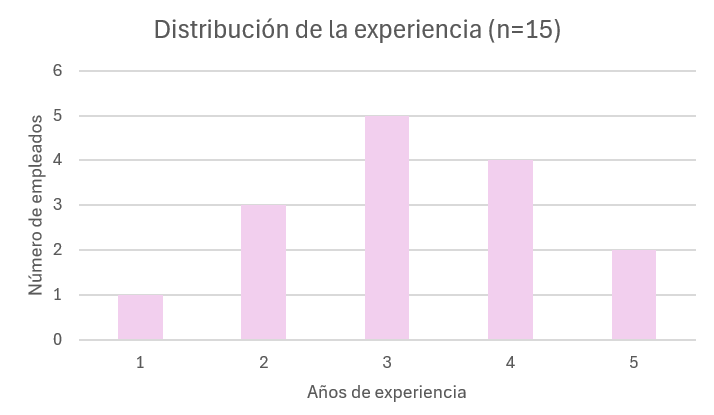
Figura 1.5: Diagrama de barras de la experiencia.

Todos los gráficos en Excel siguen en su construcción más o menos los mismos pasos que los seguidos en el diagrama de barras/columnas. Por ello, es importante que dediques cierto tiempo a revisar las distintas opciones que aparecen en la cinta del menú Diseño de gráfico.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: practica-1.

En la animación que tienes disponible en [https://www.uv.es/ticstat/diagrama_barras.gif](https://www.uv.es/ticstat/diagrama_barras.gif) encontrarás cómo se ha realizado el gráfico de columnas de la Figura 1.5.

1.3.2 Aplicación práctica 2 con Excel

Supongamos que disponemos del número de días de baja durante el último año de una muestra de 50 empleados seleccionados al azar. Estos son los datos.

Tabla 1.6: Días de baja de una muestra de 50 empleados.

0	0	8	12	0
13	5	1	14	2
11	0	2	3	14
10	8	10	4	6
19	15	0	0	15
0	9	2	10	4
18	4	1	17	11
0	19	8	13	16
2	16	12	6	0
7	11	20	0	6

En la práctica anterior construimos la tabla de frecuencias utilizando la función FRECUENCIA(). En esta práctica veremos como hacerlo utilizando las tablas dinámicas de Excel, que nos permitirá agrupar la tabla de frecuencias resultante para construir intervalos.

Abrimos un nuevo libro de Excel. Introducimos en la celda A1: Días de baja, que es nuestra variable objeto de estudio, y en el rango A2:A51 los datos que recoge la Tabla 1.6.

Para insertar una tabla dinámica seleccionamos: Insertar > Tabla dinámica > De una tabla o rango. Se abre el cuadro Tabla dinámicas desde la tabla o rango, seleccionamos el rango dondo se encuentran nuestros datos, incluida la celda A1 que tiene el nombre de la variable, y seleccionamos la celda D1 para que se cree ahí la tabla dinámica, como se muestra en la Figura 1.6. Hacemos clic en el botón Aceptar para crear la tabla.

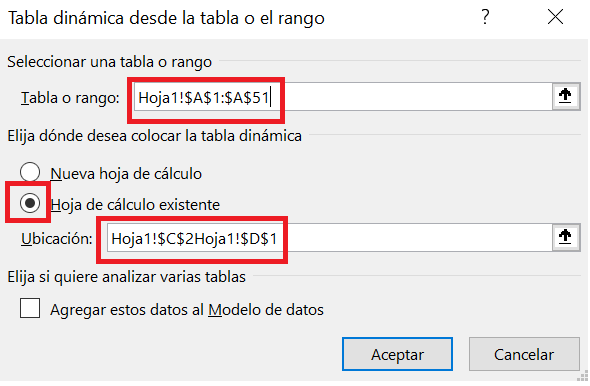
Figura 1.6: Selección de rango de datos para tabla dinámica.

Como vemos, se cre la tabla dinámica en la celda D1. En la parte derecha de la ventana aparecen los Campos de tabla dinámica. En la caja central se encuenta listada nuestra variable: Días de baja. Hacemos clic sobre ella para seleccionarla y la arrastramos hasta la caja Filas, donde la soltamos. Inmediatamente, en la columna D se listan los distintos valores que toma la variable. Ahora, volvemos a arrastrar Días de baja pero a la caja Valores. Por defecto, suma los valores y se añaden en la columna E; pero nosotros no queremos la suma sino el conteo de trabajadores. Para ello, en la caja de Valores hacemos clic sobre Suma de Días de baja > Configuración de campo de valor… > Recuento > Aceptar. Ya tenemos nuestra tabla de frecuencias.

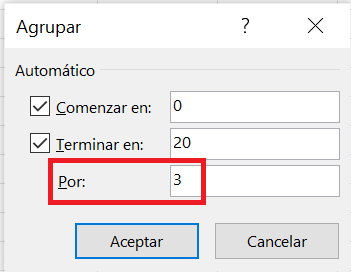
Nuestra variable Días de baja presenta 21 valores distintos con bajas frecuencias todos ellos. En este caso, si hiciésemos un diagrama de barras/columnas no resultaría informativo. En su lugar, vamos a agrupar los valores en intervalos con la única finalidad de tener una representación gráfica informativa sobre cómo se distribuyen los valores de la variable. Hacemos clic sobre cualquier celda con los valores de la variable, es decir, cualquier celda del rango D2:D22; pulsamos el botón derecho del ratón y seleccionamos Agrupar. Se abre el cuadro Agrupar (ver Figura 1.7) en el que automáticamente se fija el valor el límite inferior del primer intervalo en 0 (mínimo de la variable) y el del límite superior del último intervalo en 20 (máximo de la variable). Como tenemos 21 valores distintos para Días de baja e interesa construir intervalos de la misma amplitud, vamos a fijar la amplitud del intervalo en 3. Si queremos ampliar la amplitud a 4, para tener intervalos de misma amplitud lo que haríamos es modificar, en general, el límite superior del último intervalo teniendo en cuenta que éste tiene que contener al máximo. Pulsamos el botón de Aceptar.

Figura 1.7: Cuadro de valores para crear los intervalos.

Obtenemos una tabla de frecuencias de valores agrupados en intervalos formada por un total de 7 intervalos, todos con la misma amplitud: 3. Seleccionamos las celdas D1 y E1 y cambiamos los nombres a Días de baja y Nº de empleados, respectivamente. La tabla se reproducen en la Figura 1.8.

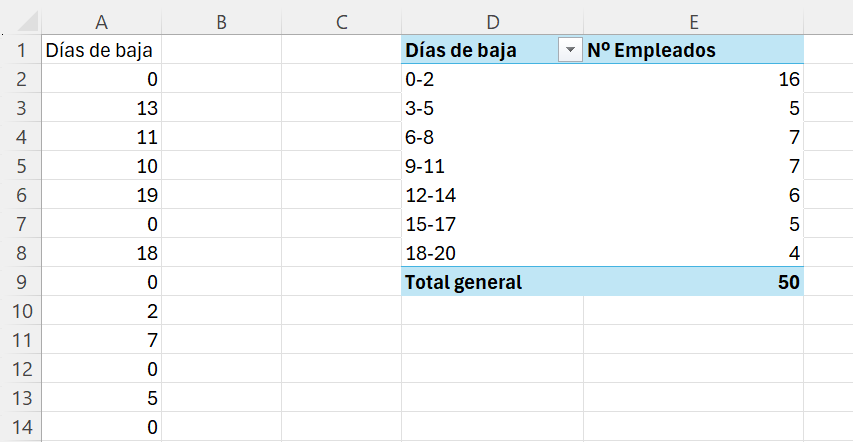
Figura 1.8: Tabla de frecuencias de valores agrupados en intervalos.

Muy importante, observad que con la tabla dinámica se crean intervalos que son cerrados por la izquierda y la derecha.

En la animación que tienes disponible en [https://www.uv.es/ticstat/tabla-dinamica-intervalos.gif](https://www.uv.es/ticstat/tabla-dinamica-intervalos.gif) encontrarás cómo se ha realizado la tabla de valores agrupados de la Figura 1.8.

Cuando los valores de la variables se encuentran agrupados en intervalos, la representación gráfica básica es un histograma. En un histograma se sitúa en el eje de abcisas (eje X) los valores de la variable agrupados en intervalos. Si los intervalos son de la misma amplitud, lo más habitual, sobre cada intervalo se construye un rectángulo cuya altura se hace corresponder con la frecuencia absoluta (conteo de número de observaciones cuyo valor cae dentro del intervalo) o relativa (tanto por uno de valores que caen dentro del intervalo).

Con los valores agrupados en intervalos como en la Figura 1.8, dibujaremos el histograma a partir de una gráfico de columnas (ver Sección 1.3.1).

Nos situamos en la celda G1 e insertamos un gráfico de columnas básico y seleccionamos los datos a representar: el rango E2:E8. Automáticamente se identifican las etiquetas del eje horizontal como los intervalos (rango D2:D8). Como es correcto no tenemos que cambiar nada. Vamos a mejorar la presentación del gráfico. Hacemos clic sobre el dibujo y seleccionamos la opción de Elementos de gráfico. Deseleccionamos Líneas de cuadrícula y seleccionamos: Títulos del eje y Etiquetas de datos. Ahora, hacemos clic sobre el símbolo > situado a la derecha de la opción Ejes y deseleccionamos Eje vertical primario. En la Figura 1.9 se muestran las opciones elegidas.

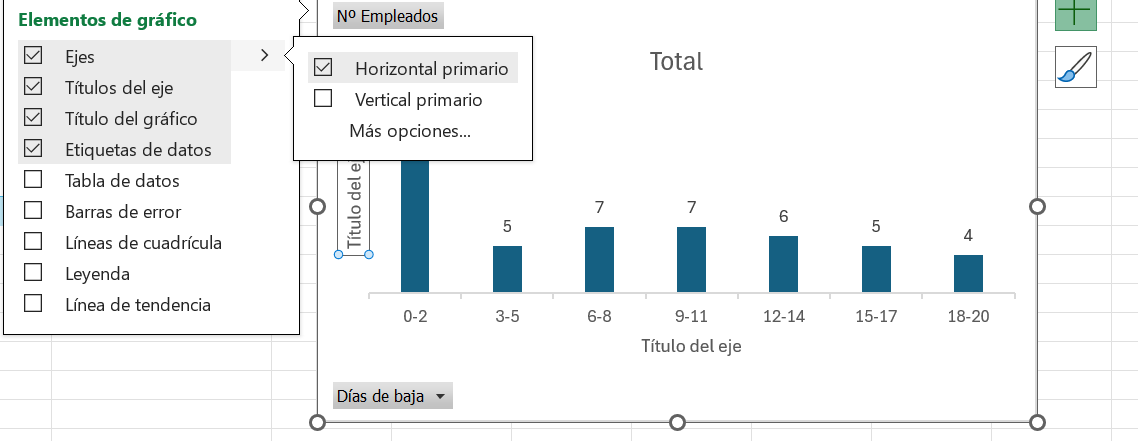
Aún tenemos un diagrama de barras. Vamos a resolver esta cuestión. Hacemos clic sobre las barras y pulsamos el botón derecho del ratos. Seleccionamos la opción: Dar formato a serie de datos…. Por defecto se muestran las opciones del tercer botón: , que hace referencia a las opciones de series.

Sustituimos los valores de Superposición de series y Ancho del rango por 0. Seguidamente, seleccionamos la opción de relleno y borde. Cambiamos el color de relleno y añadimos una línea sólida de color blanco como borde.

Por último, añadimos los títulos del histograma:

eje x: Número de días de baja.
eje Y: Número de empleados.
título principal: Histograma de los días de baja (n=50)

El histograma final será similar al siguiente:

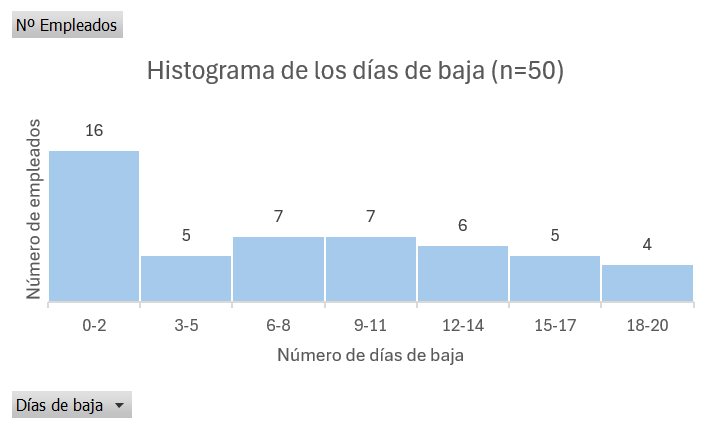
Figura 1.10: Histograma de los días de baja.

En la animación que tienes disponible en [https://www.uv.es/ticstat/thistograma.gif](https://www.uv.es/ticstat/thistograma.gif) encontrarás cómo se ha realizado el histograma a partir de la tabla de valores agrupados de la Figura 1.8.

Excel tiene un gráfico específico para dibujar histogramas a partir de los datos brutos, sin agrupar en intervalos. El inconveniente de este gráfico de Excel es que construye directamente los intervalos y no se pueden cambiar.

Vamos a comprobarlo. Nos situamos, por ejemplo, en la celda F17. Hacemos clic en Insertar, luego en el botón (Insertar gráfico de estadística) y seleccionamos: Histograma. Por defecto, se abre una plantilla vacía de dibujo. Seleccionamos como rango de datos el rango A2:A51 y Aceptar para crear el gráfico. Como resultado, obtendremos un histograma similar al que se reproducen en el Figura 1.11. Como comprobamos, Excel ha creado un histograma con 4 intervalos de amplitud 6, abiertos por la izquierda (() y cerrados por la derecha (]), salvo el primero que es cerrado por los dos extremos. Estos intervalos no los podemos modificar, es el principal inconveniente de este tipo de gráfico.

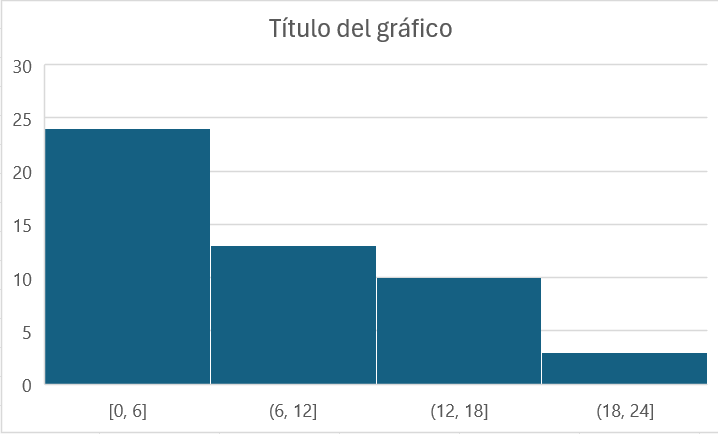
Figura 1.11: Grafico estadístico. Histograma en Excel.

Una vez hemos dibujado el histograma, podemos mejorar su apariencia como ya sabemos, cambiando los colores de relleno y borde, poniendo títulos, etc.

En la animación que tienes disponible en [https://www.uv.es/ticstat/histograma2.gif](https://www.uv.es/ticstat/histograma2.gif) encontrarás cómo se ha realizado el histograma utilizando el gráfico estadístico de Excel.

1.4 Medidas de posición

Las medidas de posición son medidas estadísticas que permiten resumir el conjunto de datos de forma que alrededor de estos valores se localizan un grupo de observaciones. Las principales medidas de posición son:

Media (aritmética)
- Media ponderada
- Otras: media geométrica, media armónica, media cuadrática.
Mediana
Moda
Cuantiles: cuartiles, deciles, percentiles, etc.

1.4.1 Media aritmética

Se denota por $\bar x$ y es la suma de todos los valores del conjunto de datos dividido por el número total de observaciones. \[\bar{x}=\frac{\displaystyle\sum_{i=1}^{n}x_i }{n}=\frac{x_1+x_2+...+x_n}{n} \tag{1.5}\]

Entre las ventajas que presenta la media cabe destacar: (1) su cálculo es sencillo e intervienen todos los valores de la distribución, (2) resulta fácil de interpretar y (3) es única. Ahora bien, si el conjunto de datos que estamos analizando presenta valores anómalos o atípicos, la media no será la mejor medida para describir o resumir dicho conjunto de datos. La media es sensible a valores extremos (ver Sección 1.8).

Ejemplo 1.7 A partir de los datos brutos del Ejemplo 1.6, calcular (a mano) la experiencia media, en años, de la muestra de empleados.

Solución: Disponemos los datos en columna, similar a como los tendríamos en un fichero para trabajarlos con el ordenador. En esta situación, para calcular la media, no es necesario ordenar los valores que toma la variable.

Tabla 1.7: Tabla cálculo de la media suponiendo frecuencias unitarias.

$x_i$
1
5
2
3
3
4
5
3
2
4
3
4
2
3
4

Si consideramos que los valores no se repiten ($i=1,2,3,...,n=15$), aplicando la Ecuación 1.5 tendremos: \[\bar{x}=\frac{\displaystyle\sum_{i=1}^{n=15}x_i }{n}=\frac{x_1+x_2+...+x_{15}}{15}=\frac{1+5+2+...+3+4}{15}=\frac{48}{15}=3.2\] Es decir, la experiencia media de los trabajadores seleccionados es de 3.2 años.

Ejemplo 1.7 con Excel. Lo más habitual cuando trabajamos con datos es que las variables se encuentren por columnas y las observaciones por filas. Además, para tratar estos datos se recurre al uso de software generealista, como Excel, o de softwre específico para el análisis estadístico como SPSS, Stata, R, etc.

Abrimos un nuevo libro de Excel. En la celda A1 escribimos el nombre de la variable: experiencia. En el rango A2:A16 introducimos los datos de la variable que hemos observado en nuestra muestra de 15 empleados.

En Excel disponemos de varias opciones para usar funciones con las que calcular la medida de interés. En general podemos:

Opción 1. Escribir la fórmula en la celda.
Opción 2. Insertar la función haciendo clic en el botón que se encuentra inmediatamente a la izquierda de la barra de fórmulas.
Opción 3. Realizar a partir del menú principal la siguiente selección: Fórmulas > Más funciones > Estadísticas > PROMEDIO

Vamos a calcular la media siguiendo la opción 1.

En la celda C1 introducimos el texto: media. Calcularemos la media en la celda D1. La función PROMEDIO() calcula la media aritmética. Como argumento de la función especificamos el rango de celdas que contiene nuestros datos. Observad que al comenzar a escribir el nombre de la función se ha abierto un cuadro en el que nos facilitaba un listado de funciones con el patrón de carácteres introducidos. Escribimos en la celda C1: =promedio(A2:16). En lugar de escribir directamente la función podíamos haberla insertado seleccionándola de entre las funciones estadísticas.

El resultado final debería ser similar al que se muestra en la Figura 1.12.

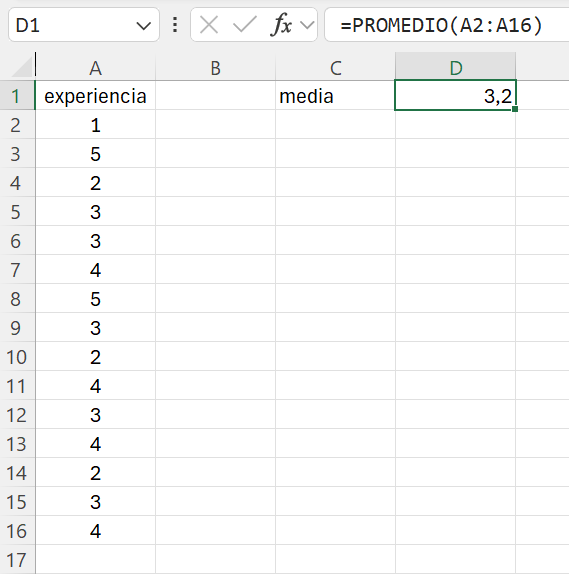
Figura 1.12: Resolución del Ejemplo 1.7. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_7.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_7_excel.gif](https://www.uv.es/ticstat/ej_1_7_excel.gif) encontrarás cómo calcular la media a partir de las tres opciones anteriores.

Sin embargo, cuando observamos que hay valores de la variable que se repiten y queremos calcular la media a mano, lo más habitual es organizar el conjunto de datos en una tabla de frecuencias (por ejemplo, Tabla 1.1 o Tabla 1.2). Dispuestos así los datos, la expresión equivalente que se utiliza para calcular la media es: \[\bar x = \frac{\displaystyle\sum_{i=1}^I x_i \cdot n_i}{n} \tag{1.6}\] donde $I$ es el número de valores distintos que toma la variable y $n$ es el número total de observaciones (en este caso, el tamaño de la muestra).

Independientemente del número de observaciones que tengamos, los softwares calculan la media, y resto de medidas estadísticas, a partir de los datos brutos, como hemos hecho en el Ejemplo 1.7. Construir una tabla de frecuencias es algo que hacemos para poder hacernos una idea de cómo se distribuye la variable o, por ejemplo, para adjuntar la tabla en un informe.

Ejemplo 1.8 Construir una tabla estadística a partir de los datos del Ejemplo 1.6. y calcular (a mano) la media de la variable $X$, que recordemos es la experiencia de los empleados.

Solución: A partir de los datos brutos de la variable $X$ hemos construido la Tabla 1.8. La variable $X$ toma los valores $x_i \quad (i=1,2,3,4,5)$, que ordenados de menor a mayor son: $x_1=1$, $x_2=2$, $x_3=3$, $x_4=4$ y $x_5=5$ (columna 1). Por tanto, la variable $X$ toma 5 distintos valores ($I=5$). Ahora, contamos cuantas veces se repite cada valor (columna 2). Así, el primer valor se repite 1 vez ($n_1=1$), el segundo valor se repite 3 veces ($n_2=3$), el tercer valor se repite 5 veces ($n_3=5$), el cuarto se repite 4 veces ($n_4=4$) y el último valor se repite 2 veces ($n_5=2$).

Tabla 1.8: Cálculo de la media a partir de la tabla de frecuencias.

$x_i$	$n_i$	$x_i \cdot n_i$
$x_1$ 1	1 $n_1$	1 $x_1\cdot n_1$
$x_2$ 2	3 $n_2$	6 $x_2\cdot n_2$
$x_3$ 3	5 $n_3$	15 $x_3\cdot n_3$
$x_4$ 4	4 $n_4$	16 $x_4\cdot n_4$
$x_5$ 5	2 $n_5$	10 $x_5\cdot n_5$
	———	————
	$n=15$	$\sum=48$

Una vez construida la tabla estadística con las frecuencias $n_i$ (columnas 1 y 2), hacemos uso de la fórmula de la media dada en la Ecuación 1.6. En el numerador tenemos que calcular, para cada $i$, el producto $x_i \cdot n_i$ y sumarlos, es decir: \[x_1 \cdot n_1 +x_2 \cdot n_2+x_3 \cdot n_3 + x_4 \cdot n_4 + x_5 \cdot n_5\] Para facilitar estos cálculos, a la tabla de frecuencias le añadimos una tercera columna ($x_i \cdot n_i$) que es el producto de la primera columna por la segunda. Si sumamos los valores de la tercera columna estamos obteniendo que:\[\displaystyle\sum_{i=1}^{I=5}x_i \cdot n_i = 48\] Este valor significa que, en total, los 15 empleados seleccionados acumulan una experiencia (antigüedad en la empresa) de 48 años.

Por tanto: \[\bar x = \frac{\displaystyle\sum_{i=1}^I x_i \cdot n_i}{n}=\frac{48}{15}=3.2\] En media, la experiencia de los empleados es de 3.2 años.

Ejemplo 1.8. con Excel. En Excel, para calcular la media a partir de una tabla de frecuencias, tenemos dos opciones:

opción 1. Reproducir los pasos que realizamos para calcular a mano la media a partir de la tabla de frecuencias.
opción 2. Utilizar la función SUMAPRODUCTO() para calcular el númerador de la Ecuación 1.6, que es la suma del producto $x_i \cdot n_i$.

Con la opción 1, suponiendo que ya tenemos los datos del ejercicio en el rango A2:A16 y sabiendo que el número de empleados toma 5 distintos valores ($I=5$) que introducimos en el rango C2:C6, escribimos en la celda D1 el texto ni y construimos la tabla de frecuencias utilizando la función frecuencia() seleccionando el rango D2:D6 (ver Sección 1.3.1). Escribimos en la celda E1 el texto xi*ni, en la celda E2 introducimos la fórmula: =C2*D2. Arrastramos el contenido de la celda E2 hasta la celda E6 para copiar su contenido.

En este punto, tenemos los distintos productos $x_i \cdot n_i$. Si sumamos el rango E2:E6 tendremos el numerador de la Ecuación 1.6. Por tanto, el valor de la media será el cociente entre esta suma y el tamaño de la muestra: 15, que es la suma del rango D2:D6. En la celda D8 escribimos el texto media, y en la celda E8 la fórmula: =suma(E2:E6)/suma(D2:D6). El resultado de la media será 3.2

Con la opción 2 obtenemos directamente la suma de los distintos productos $x_i \cdot n_i$, ahorrándonos tener que calcular los resultados del rango E2:E6. Por ejemplo, escribimos en la celda D9 el texto media, y en la celda E9 la fórmula: =sumaproducto(C2:C6;D2:D6)/suma(D2:D6).

Como hemos podido comprobar, la función SUMAPRODUCTO() ahorra muchos cálculos; es una función que conviene recordar porque suele utilizarse con frecuencia.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_8.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_8_excel.gif](https://www.uv.es/ticstat/ej_1_8_excel.gif) encontrarás cómo calcular la media a partir de las dos opciones anteriores.

El resultado final debería ser similar al que se muestra en la Figura 1.13.

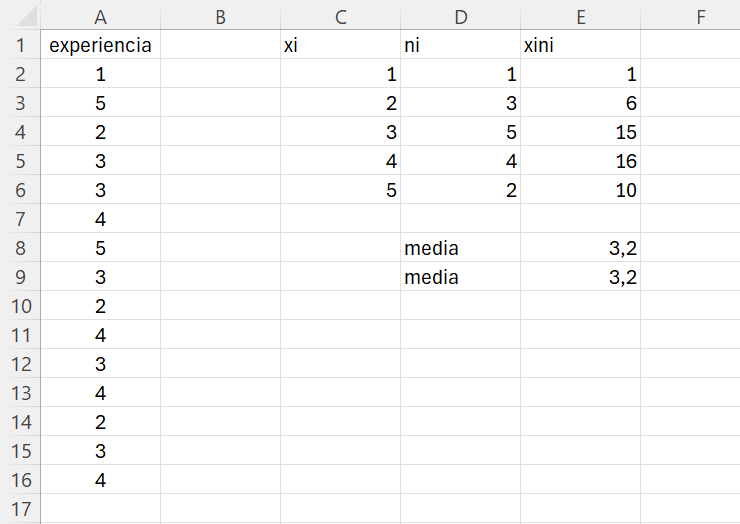
Figura 1.13: Resolución del Ejemplo 1.8. con Excel.

Si estamos trabajando con la población la media se denota por $\mu$ y se expresa de la siguiente forma:\[\mu= \frac{\displaystyle\sum_{i=1}^N x_i}{N} \quad o \quad \mu= \frac{\displaystyle\sum_{i=1}^I x_i \cdot n_i}{N}\] En este caso $N$, número total de observaciones, sería el tamaño de la población.

1.4.1.1 Propiedades de la media

La media (aritmética) presenta las siguiente propiedades.

La suma de las desviaciones de los valores de la variable respecto de su media es cero. Es decir, \[\sum\limits_{i = 1}^n {({x_i}} - \bar x)=0 \tag{1.7}\] o similarmente, si disponemos de la tabla de frecuencias \[\sum\limits_{i = 1}^I {({x_i}} - \bar x) \cdot {n_i}=0 \tag{1.8}\]
La media es el centro de gravedad del conjunto de datos.
La media de una variable cambia si se aplican cambios de origen y/o de escala.
En general: \[\bar{x}=\frac{\displaystyle\sum_{i=1}^{k}\bar{x}_i \cdot N_i}{\displaystyle\sum_{i=1}^{k}N_i}=\frac{\bar{x}_1 \cdot N_1+\bar{x}_2 \cdot N_2+...+\bar{x}_k \cdot N_k}{N_1+N_2+...+N_k} \tag{1.9}\] donde $\bar{x}_i$ (i=1,2,..,k) corresponde a la media de cada uno de los k grupos distintos, y $N_i$ (i=1,2,..,k) es el tamaño de los respectivos grupos. Esta propiedad es importante porque nos dice que a partir del conocimiento de las medias y tamaños de k grupos podemos conocer la media del conjunto (la media global es la media de medias). En definitiva, la media global es una media ponderada (apartado Sección 1.4.2) de las medias de los $k$ grupos.

Un cambio de origen, que se suele denotar por $a$, se produce cuando todos los valores de la variable se desplazan porque se les suma o resta una constante.

Un cambio de escala o unidad, que suele denotarse por $b$, se produce cuando todos los valores de la variable se multiplican o dividen por una constante.

Las medidas estadísticas (media, varianza, coeficiente de variación, correlación, etc.) pueden verse o no afectadas por los cambios de origen y/o los cambios de escala. En este curso introductorio no vamos a abordar esta cuestión, el lector interesado puede consultar el capítulo 7 de Coll-Serrano (2023).

Ejemplo 1.9 La empresa A cuenta con 150 empleados y el salario medio es de 1,400 euros. La empresa B tiene 125 empleados y el salario medio es de 1,450 euros. Por último, la empresa C tiene 200 trabajadores y la media del salario se sitúa en 1,525 euros.

¿Cuál es el salario medio en el conjunto de las tres empresas?

Solución: Resumimos la información de la que disponemos en la siguiente tabla:

Tabla 1.9: Datos del Ejemplo 1.9.

A ($k=1$)	$\rightarrow$	$N_A=150$	$\bar{S}_A=1,400$
B ($k=2$)	$\rightarrow$	$N_B=125$	$\bar{S}_B=1,450$
C ($k=3$)	$\rightarrow$	$N_C=200$	$\bar{S}_C=1,525$

Como tenemos 3 grupos ($k=3$), de los que conocemos su tamaño y la media de la característica de interés (el salario), aplicamos la propiedad 4 de la media para calcular la media del salario considerando el conjunto de las 3 empresas. \[\bar{S}=\frac{\displaystyle\sum_{i=1}^{k=3}\bar{x}_i \cdot N_i}{\displaystyle\sum_{i=1}^{k=3}N_i}=\frac{\bar{x}_1 \cdot N_1+\bar{x}_2 \cdot N_2+\bar{x}_3 \cdot N_3}{N_1+N_2+N_3}=\frac{1,400\cdot150+1,450\cdot125+1,525\cdot200}{150+125+200}\] \[\bar{S}=\frac{696,250}{475}=1,465.789\] Por tanto, conocido el tamaño de cada grupo y su media, hemos podido calcular la media del conjunto. El salario medio considerando el conjunto de las tres empresas se sitúa en 1,465.789 euros.

Ejemplo 1.10 De acuerdo con los datos de la Encuesta de Estructura Salarial, en España había en 2018 un total de 10,006,679 trabajadores con contrato de trabajo indefinido, siendo su salario bruto anual medio de 25,776.23 euros. Con contrato de duración temporal se encontraban 2,969,396 trabajadores, que tenían un salario bruto anual medio de 18,054.08 euros.

Conociendo estos resultados, calcular el salario bruto anual medio del conjunto de trabajadores.

Solución: Para calcular el salario medio del conjunto de los trabajadores recurrimos a la propiedad 4 de la media y aplicamos la Ecuación 1.9.\[Salario\_bruto\_anual\_medio = \displaystyle\frac{25,776.23 \cdot 10,006,679 + 18,054.08 \cdot 2,969,395}{10,006,679+2,969 ,395}\] \[Salario\_bruto\_anual\_medio =\frac{311,544,154,300}{12,976,074}=24,099.12\] Así pues, el salario bruto medio anual en 2018 se situó en 24,099.12 euros.

En el Ejemplo 1.9 y Ejemplo 1.10 hemos estado trabajando ¿con una muestra o con la población?

1.4.2 Media ponderada

Si a cada uno de los valores de la variable ($x_i$) se le atribuye un determinado peso ($\omega_i$), la media de los valores será una media ponderada ($\bar x_\omega$) tal que: \[ \bar {x}_\omega = \frac{\sum\limits_{i=1}^{n} x_i \cdot \omega_i}{\sum\limits_{i=1}^{n}\omega_i} \tag{1.10}\]

Si observamos la expresión anterior nos daremos cuenta que la media (aritmética) es una media ponderada en la que los pesos se corresponden con las frecuencias.

Ejemplo 1.11 Supongamos que la evaluación final de una materia es: un examen final que supone el $70\%$ de la calificación y tres pruebas a lo largo del curso que suponen las dos primeras un $5\%$ y un $20\%$ la tercera.
Un estudiante ha obtenido las siguientes calificaciones:

prueba 1: 8 puntos
prueba 2: 5 puntos
prueba 3: 7 puntos
examen final: 8 puntos

¿Cuál es la nota media de este estudiante?

Solución: Para calcular la nota media del estudiante aplicamos la expresión de la media ponderada: \[\bar {x}_\omega = \frac{\sum\limits_{i=1}^{n=4} x_i \cdot \omega_i}{\sum\limits_{i=1}^{n=4}\omega_i}=\frac{8\cdot0.05+5\cdot0.05+7\cdot0.2+8\cdot0.7}{0.05+0.05+0.2+0.7}=\frac{7.65}{1}=7.65\]

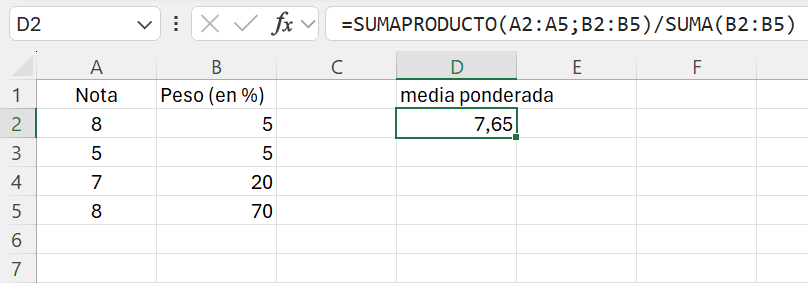
Ejemplo 1.11. con Excel. Abrimos un nuevo libro de Excel. En la celda A1 escribimos Nota, y en la celda B1 escribimos Peso (en %). Introducimos los datos a los que hace referencia el ejercicio 11. En la celda D1 escribimos media ponderada. Esta medida la vamos a calcular en la celda D2. Si nos fijamos en la expresión de la media ponderada, el numerador se obtiene multiplicando cada valor $x_i$ por su correspondiente peso $w_i$ y luego sumando todos los productos. Para realizar este cálculo utilizamos la función SUMAPRODUCTO(). El resultado lo tenemos que dividir por la suma de los pesos. Por tanto, en la celda D2 escribiremos: =sumaproducto(A2:A5:B2:B5)/suma(B2:b5). La nota media será de 7.65 puntos.

El resultado final debería ser similar al que se muestra en la Figura 1.14.

Figura 1.14: Resolución del ejemplo 1.11. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_11.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_11_excel.gif](https://www.uv.es/ticstat/ej_1_11_excel.gif) encontrarás cómo calcular la media ponderada.

1.4.3 Mediana

La mediana, que se denota por $Me$, es un valor del recorrido de la variable que acumula aproximadamente el 50% de las observaciones. Es decir, la mediana es el valor que divide la distribución de frecuencias de una variable en dos partes, de forma que alrededor del 50% de las observaciones quedan por debajo de ese valor y aproximadamente el 50% por encima. Por esta razón, porque la mediana divide las observaciones en dos partes, a la mediana no le afectan los valores atípicos.

La mediana, y en general los cuantiles, son medidas aproximadas. Existen distintos algoritmos para su cálculo. Volveremos sobre esta cuestión más adelante.

Si partimos de la distribución de frecuencias de valores sin agrupar de una variable, para calcular la mediana seguimos los siguientes pasos:

Paso 1. Ordenamos los valores de la variable ($x_i$) de menor a mayor y calculamos las frecuencias acumuladas ($N_i$).
Paso 2. Buscamos la primera frecuencia acumulada $N_i$ que sea igual o mayor al número de observaciones que acumula la mediana (y que es $\frac{n}{2}$).
Paso 3. Identificamos los valores de interés. Una vez identificado $N_i$, también tenemos identificado el valor de la variable $x_i$ que acumula esas observaciones, así como la frecuencia acumulada anterior $N_{i-1}$ y el valor de la variable $x_{i+1}$.
Paso 4. Aplicamos la siguiente regla. \[\text{Si} \quad \left\{\begin{matrix} N_{i-1}<\displaystyle\frac{n}{2}<N_i & \Rightarrow & Me=x_i\\ \\ N_i=\displaystyle\frac{n}{2} & \Rightarrow & Me = \displaystyle\frac{x_i + x_{i+1}}{2} \end{matrix}\right. \tag{1.11}\]

Si los valores de la variable se encuentran agrupados en intervalos, con el procedimiento anterior podemos conocer el intervalo donde se encontrará la mediana, pero no vamos a tratar como obtener su valor aproximado. Si estáis interesados en su cálculo podéis consultar: Esteban (2005).

Ejemplo 1.12 A partir de la tabla de frecuencias construida en el Ejemplo 1.6, vamos a calcular la experiencia mediana de los trabajadores.

Tabla 1.10: Tabla de frecuencias del ejemplo 1.12.

$x_i$	$n_i$	$N_i$
1	1	1
2	3	4
3	5	9
4	4	13
5	2	15

Solución: Aplicamos el procedimiento descrito anteriormente:

Paso 1. Añadimos una tercera columna a tabla estadística para calcular las frecuencias absolutas acumuladas ($N_i$).

Paso 2 y 3. Nos preguntamos, ¿aproximadamente, cuántas observaciones quedan por debajo de la mediana? La respuesta: $\frac{n}{2}=\frac{15}{2}=7.5\hspace{2mm}trabajadores$

En la columna 3, buscamos la primera frecuencia acumulada que es igual a superior a 7.5. Esto es $N_i=N_3=9$, a esta frecuencia acumulada le corresponde el valor $x_i=x_3=3$. También identificamos los valores $N_{i-1}=4$ y $x_{i+1}=4$.

Paso 4. Aplicamos la regla de decisión. Como $N_{i-1}=4<\frac{n}{2}=7.5<N_i=9 \quad\Rightarrow\quad Me=X_i=3$

Así, podemos decir que aproximadamente el 50% de los trabajadores entrevistados tienen una experiencia menor o igual a 3 años.

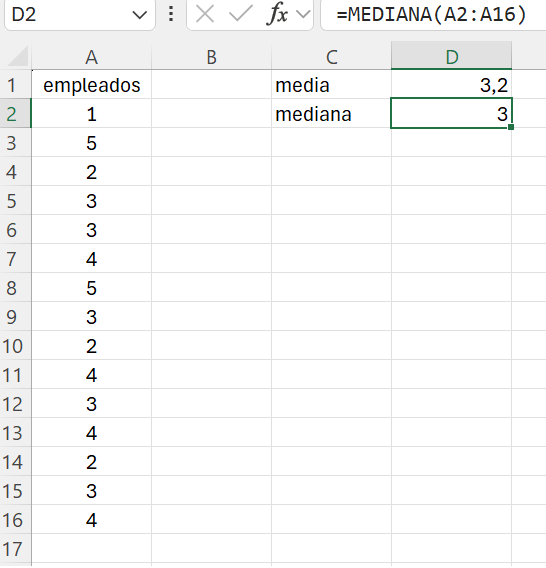
Ejemplo 1.12. con Excel. Con Excel podemos calcular la mediana a partir de los datos dispuestos por columnas. Así pues, abrimos el fichero ej_1_7.xlsx. En la celda C2 escribimos mediana. Para calcular la mediana utilizamos la función MEDIANA(). Vamos a realizar el cálculo en la celda D2, escribimos: =mediana(A2:A16). La mediana es 3.

El resultado final debería ser similar al que se muestra en la Figura 1.15.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_12.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_12_excel.gif](https://www.uv.es/ticstat/ej_1_12_excel.gif) encontrarás cómo calcular la mediana.

Figura 1.15: Resolución del ejemplo 1.12. con Excel.

1.4.4 Moda

La moda es el valor de la variable que más se repite; esto es, el valor que tiene una mayor frecuencia (absoluta, $n_i$ ; o relativa, $f_i$).

Ejemplo 1.13 Atendiendo a la distribución de frecuencias obtenida en el Ejemplo 1.6 (Tabla 1.10), ¿cuál es la experiencia, en años, más habitual en los trabajadores analizados?

Solución: La experiencia más habitual/frecuente es la moda. En este caso, la experiencia más frecuente entre los trabajadores seleccionados es una experiencia de 3 años, que es la experiencia de un total de 5 empleados.

Ejemplo 1.13. con Excel. Abrimos el fichero ej_1_12.xlsx. En la celda C3 escribimos moda. En Excel tenemos dos fórmulas para calcular la moda:

MODA.UNO(): devuelve el valor más frecuente o repetitivo de una matriz o rango de datos.
MODA.VARIOS(): devuelve una matriz vertical de los valores más frecuentes o repetitivos de una matriz o rango de datos.

En el ejemplo que estamos trabajando tenemos pocos datos y fácilmente podemos observar que sólo hay un valor que se repite con la mayor frecuencia; pero, ¿y si tenemos muchos datos? Vamos a calcular la moda utilizando la función MODA.VARIOS(). En la celda D3 escribimos y ejecutamos: =moda.varios(A2:A16). La moda es 3. En este caso, la función sólo devuelve un valor, si hubiese más de una moda se listarían los valores modales uno debajo del otro.

El resultado final debería ser similar al que se muestra en la Figura 1.16.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_13.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_13_excel.gif](https://www.uv.es/ticstat/ej_1_13_excel.gif) encontrarás cómo calcular la moda.

Figura 1.16: Resolución del ejemplo 1.13. con Excel.

En el caso de que los valores de la variable se hayan agrupado en intervalos de la misma amplitud, el intervalo modal será aquel que también tenga una mayor frecuencia. Sin embargo, si los intervalos se han construido con distinta, será necesario calcular la altura ($h_i$) de cada intervalo para obtener el intervalo modal: el intervalo de mayor altura.

La altura del intervalo se obtendrá al dividir la frecuencia del intervalo ($n_i$) entre la amplitud del mismo ($a_i$). \[h_i=\frac{n_i}{a_i}\]

Identificado el intervalo modal, podemos calcular el valor modal. No lo trato en este manual, pero si estáis interesados en cómo obtener en este caso el valor de la moda podéis consultarlo en: Esteban (2005).

Ejemplo 1.14 Una muestra de 1,000 trabajadores de una empresa multinacional con sede en la provincia de Valencia presenta la siguiente información relativa a los salarios (en euros).

Tabla 1.11: Datos del Ejemplo 1.14.

Salarios	Trabajadores
$[1,000-1,500[$	150
$[1,500-2,000[$	200
$[2,000-2,500[$	300
$[2,500-3,000[$	250
$[3,000-3,500[$	75
$[3,500-4,000]$	25

¿En que intervalo salarial se sitúa la moda?

Solución: Como todos los intervalos tienen la misma amplitud, el intervalo salarial $[2,000-2,500[$ es el que más se repite, en este intervalo salarial se encuentran 300 trabajadores de la muestra analizada.

1.4.5 Cuantiles

Los cuantiles son medidas de posición de tendencia no central que dividen la distribución de frecuencias. Los cuantiles más habituales son aquellos que dividen la distribución de frecuencias en 4 partes ($k=4$) (Cuartiles, $s=\{1,2,3\}$); o en 10 partes ($k=10$) (Deciles, $s=\{1,2,...,9\}$); o en 100 partes ($k=100$) (Percentiles, $s=\{1,2,...,99\}$).

No se calcula el cuartil 4 ($s=4$), o el decil 10 ($s=10$), o el percentil 100 ($s=100$). En todos estos casos el valor del cuantil es igual al máximo valor de la variable (acumulan el 100% de las observaciones).

Para calcular los cuantiles seguimos los mismos pasos que los utilizados para el cálculo de la mediana (que es un cuantil) y hacemos uso de la siguiente regla general:\[ \text{Si} \quad \left\{\begin{matrix} N_{i-1}<\displaystyle\frac{s \cdot n}{k}<N_i & \Rightarrow & Q_{s}=x_i\\ \\ N_i=\displaystyle\frac{s \cdot n}{k} & \Rightarrow & Q_{s} = \displaystyle\frac{x_i + x_{i+1}}{2} \end{matrix}\right. \tag{1.12}\] donde $Q_{s}$ es el cuantil que se quiere calcular, $N_i$ es la primera frecuencia igual o mayor al porcentaje de observaciones $\frac{s}{k}$ que se quiere acumular y $n$ es el número total de observaciones.

Ejemplo 1.15 A partir de la tabla de frecuencias del Ejemplo 1.12, que se reproduce más abajo, calcular el primer cuartil ($C_1$), el cuarto decil ($D_4$) y el sexagésimo percentil ($P_{60}$).

Tabla 1.12: Datos del Ejemplo 1.15.

$x_i$	$n_i$	$N_i$
1	1	1
2	3	4
3	5	9
4	4	13
5	2	15

Solución: Recordemos que la variable objeto de estudio es X=“Experiencia de los empleados (en años)” y que las unidades observadas (frecuencias) son empleados.

El primer cuartil ($s=1$, $k=4$) es el valor del recorrido de la variable que deja por debajo el 25% de las observaciones, esto es, $\displaystyle\frac{s \cdot n}{k}=\frac{15}{4} = 3.75$ empleados. Por tanto, identificamos la primera frecuencia acumulada $N_i$ igual o superior a 3.75; en este caso: $N_2=4$. A esta frecuencia acumulada le corresponde el valor $x_2=2$. Identificamos los valores $N_{i-1}=N_1=1$ y $x_{i+1}=x_3=3$.

Aplicamos la regla de decisión: como $N_1=1 < 3.75 < N_2=4 \rightarrow C_1=x_2=2$ años. Aproximadamente el 25% de los empleados tienen una experiencia de 2 años o menos.
Para calcular el cuarto decil ($s=4$, $k=10$), primero obtenemos las observaciones que aproximadamente deja por debajo: $\displaystyle\frac{s \cdot n}{k}=\frac{4\cdot15}{10} = 6$ empleados. Identificamos la primera frecuencia acumulada igual o superior a 6 ($N_i=N_3=9$) y demás valores de interés: $x_i=x_3=3$,$N_{i-1}=N_2=4$ y $x_{i+1}=x_4=4$.

Aplicamos la regla de decisión: como $N_2= 4< 6 < N_3=9 \rightarrow D_4=x_3=3$ años. El 40% de los empleados de la empresa tienen una experiencia de 3 años o menos. Alternativamente, aproximadamente el 60% de los trabajadores tiene una experiencia de 3 años o más.
Por último, el sexagésimo percentil ($s=60$, $k=100$) será el valor del recorrido de la variable que deje aproximadamente el 60% de las observaciones por debajo de su valor; es decir: $\displaystyle\frac{s \cdot n}{k}=\frac{60\cdot15}{100} = 9$ trabajadores. En este caso, la primera $N_i$ igual o superior a 9 es: $N_i=N_3=9$. Como anteriormente, identificamos los restantes valores de interés: $x_i=x_3=3$,$N_{i-1}=N_2=4$ y $x_{i+1}=x_4=4$.

Aplicamos la regla de decisión: como $N_2=4< 9$ pero $9 \nless N_3=9$ sino que $\displaystyle\frac{s \cdot n}{k}=9=N_3$ entonces: $P_{60}=\displaystyle\frac{x_i+x_{i+1}}{2}=\frac{x_3+x_4}{2}=\frac{3+4}{2}=3.5$ años. Con lo que podemos decir que aproximadamente el 60% de los empleados de la empresa tienen una experiencia de 3.5 años o menos.

Ejemplo 1.15. con Excel. Con la hoja de cálculo Excel podemos calcular cuantiles a partir del cáculo de cuartiles y percentiles. Tenemos disponibles las siguientes funciones:

CUARTIL.EXC()
CUARTIL.INC()
PERCENTIL.EXC()
PERCENTIL.INC()

Con las funciones que tienen la extensión .inc podemos calcular el mínimo o el máximo; las que tienen la extensión .exc excluyen esta posibilidad, se corresponde con la nota de la explicación teórica.

Las funciones para calcular los cuartiles tienen dos argumentos; el primero es la matriz/rango con los datos, el segundo es el cuartil a calcular: 1 para el primer cuartil, 2 para el segundo y 3 para el tercero.

Las funciones para los percentiles también tienen dos argumentos; el primero para seleccionar los datos, el segundo para indicar el percentil $k$ que queremos calcular. $k$ toma valores entre 0 (sería el mínimo) y 1 (sería el máximo). Si quisiésemos calcular el percentil 78 el valor de k sería 0.78.

Explicado el uso de las funciones, vamos a calcular las medidas a las que se refiere el Ejemplo 1.15

Abrimos el fichero ej_1_13.xlsx. Escribimos cuartil 1, decil 4 y percentil 60 en las celdas C4, C5 y C6 respectivamente. En las celdas contiguas escribimos y ejecutamos las siguientes fórmulas:

=cuartil.exc(A2:A16;1)
=percentil.exc(A2:A16;0,4) (nota: calculamos los deciles como percentiles)
=percentil.exc(A2:A16;0,6)

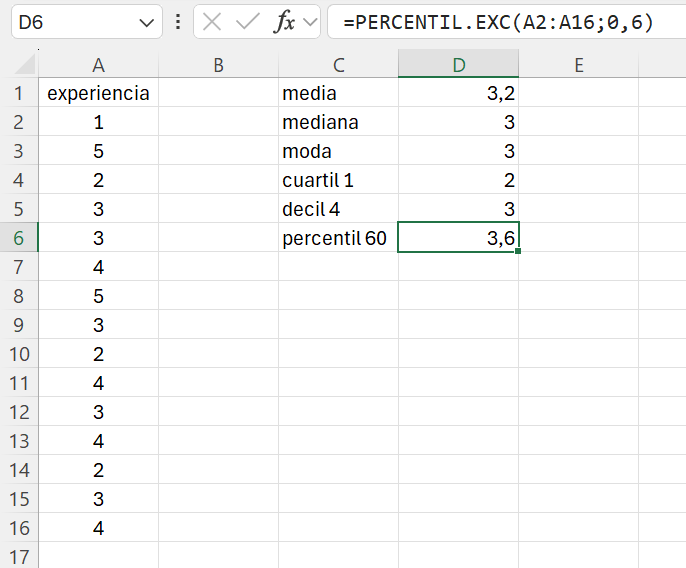
El cuartil 1 es 2 años; el decil 4 es 3 años; y el percentil 60 es 3.6 años. Observad que hay una ligera diferencia en le percentil 60 entre el cálculo realizado a mano y el resultado de Excel.

La mediana, y en general los cuantiles, son medidas aproximadas. Existen distintos algoritmos para su cálculo. Volveremos sobre esta cuestión más adelante.

El resultado final debería ser similar al que se muestra en la Figura 1.17.

Figura 1.17: Resolución del ejemplo 1.15. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_15.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_15_excel.gif](https://www.uv.es/ticstat/ej_1_15_excel.gif) encontrarás cómo calcular la moda.

1.5 Medidas de dispersión

Las medidas de dispersión son medidas estadísticas que informan sobre la variabilidad de la variable, es decir, cómo de alejados o cercanos se encuentran los valores de las observaciones de la variable.

Existen medidas de dispersión absoluta y de dispersión relativa, estas últimas se utilizan para realizar comparaciones entre variables. Algunas medidas comúnes de dispersión son:

Dispersión absoluta:
- Rango
- Recorrido intercuartílico
- Varianza
- Desviación típica
- Otras: desviación mediana, desviación media
Dispersion relativa:
- Recorrido intercuartílico relativo
- Coeficiente de variación

Hay otras medidas de dispersión, pero las anteriores son las que normalmente se estudian en un curso introductorio de estadística.

1.5.1 Rango

El rango o recorrido ($Re$) es la diferencia entre el máximo y el mínimo valor que toma la variable. \[Re=x_{max}-x_{min} \tag{1.13}\] El principial inconveniente de esta medida es que en su cálculo únicamente intervienen dos observaciones, observaciones que por otro lado pueden ser atípicas (ver apartado Sección 1.8).

Ejemplo 1.16 Considerando los datos facilitados en el Ejemplo 1.6, calculad el rango o recorrido de la variable “experiencia de los empleados”.

Solución La experiencia de los empleados va de 1 año (menor valor) a 5 años (mayor valor), es decir, el rango es 4 años. También puede decirse que el recorrido de la variable es $1-5$ (de 1 a 5 años), o que la variación máxima en la experiencia es de 4 años.

Ejemplo 1.16.con Excel. Calcularemos el rango o recorrido de la variable calculando la diferencia entre el valor máximo y el mínimo.

Abrimos el fichero ej_1_15.xlsx.

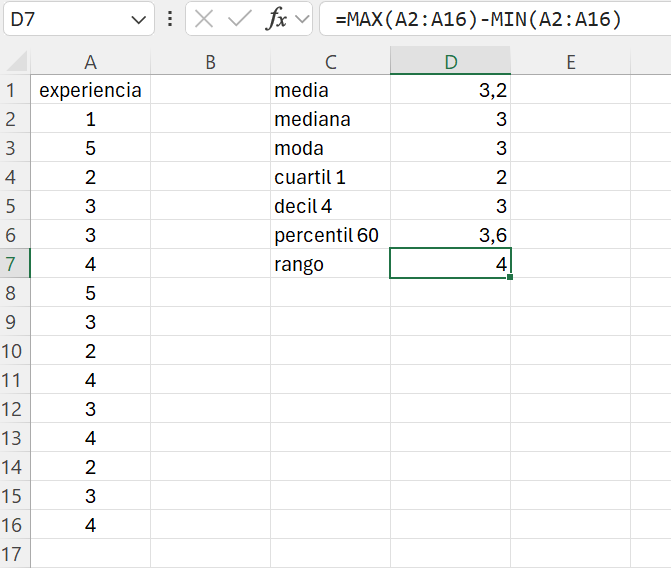
En la celda C7 escribimos rango. En la celda D7 introducimos la siguiente fórmula: =max(A2:A16) - min(A2:A16). El rango de los empleados en la muestra analizada es de 4 años.

El resultado final debería ser similar al que se muestra en la Figura 1.18.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_16.

Figura 1.18: Resolución del ejemplo 1.16. con Excel.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_16_excel.gif](https://www.uv.es/ticstat/ej_1_16_excel.gif) encontrarás cómo calcular el rang o recorrido de la variable.

1.5.2 Recorrido intercuartílico

El recorrido intercuartílio ($RIC$) es la diferencia entre el tercer y el primer cuartil. \[RIC=C_3-C_1 \tag{1.14}\] Con el recorrido intercuartílico (RIC) estamos midiendo la variabilidad del 50% de las observaciones centrales, es decir, el 50% de las observaciones se localizarán dentro del RIC, entre el primer y el tercer cuartil. A diferencia del rango, al RIC no le influyen las observaciones extremas. En el Sección 1.8 veremos que un criterio que puede utilizarse para detectar observaciones anólamas se basa en el cálculo del RIC.

Ejemplo 1.17 Calcular el recorrido intercuartílico de la experiencia de la muestra analizada a partir de la siguiente tabla de frecuencias.

Tabla 1.13: Datos del Ejemplo 1.17.

$x_i$	$n_i$	$N_i$
1	1	1
2	3	4
3	5	9
4	4	13
5	2	15

Solución En el Ejemplo 1.15 ya calculamos el primer cuartil de la variable experiencia, obteniendo que $C_1=2$

Vamos a calcular el tercer cuartil ($C_3\rightarrow\hspace{1mm}s=3\hspace{1mm},k=4$), que será el valor del recorrido que sitúe a aproximadamente el 75% de los trabajadores por debajo de ese valor, esto es, a 11.25 trabajadores.

Aplicando el algoritmo de cálculo, buscamos la primera frecuencia acumulada que sea igual o superior a 11.25. En este caso tenemos que se trata de $N_4=13$, siendo $x_4=4$. Según la regla de decisión, como $N_3=9<\frac{3\cdot n}{4}=11.25<N_4=13$, entonces el valor del tercer cuartil será $C_3=x_4=4$

Así, el recorrido intercuartílico de la experiencia es: \[RIC=C_3-C_1=4-2=2\text{ años}\]

Ejemplo 1.17. con Excel. No hay una función específica en Excel para calcular el recorrido intercuartílico, tenemos que calcularlo según la Ecuación 1.14. Ya sabemos la diferencia entre las funciones CUARTIL.EXC() y CUARTIL.INC(), podemos utilizar cualquiera de las dos para obtener el recorrido intercuartílico.

En la celda C7 escribimos ric y en la celda D7 introducimos y ejecutamos la fórmula: =cuartil.exc(A2:A16;3) - cuartil.exc(A2:A16;1), obteniendo un resultado de 2.

El resultado final debería ser similar al que se muestra en la Figura 1.19.

Figura 1.19: Resolución del ejemplo 1.17. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_17.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_17_excel.gif](https://www.uv.es/ticstat/ej_1_17_excel.gif) encontrarás cómo calcular el recorrido intercuartílico.

Desde un punto de vista teórico, si una variable presenta mucha asimetría (ver Sección 1.6.1) o valores extremos (ver Sección 1.8) es recomendable utilizar la mediana y el RIC como medidas de posición y dispersión en lugar de la media y la desviación típica

1.5.3 Varianza

La varianza se define como la media de las desviaciones cuadráticas de cada valor de la variable respecto de su media.

La varianza muestral se denota por $S^2$. Así, la varianza de una variable X será:\[ {S_X^2}=\frac{ \displaystyle\sum_{i=1}^{n}\left (x_i - \bar{x} \right )^2 }{n-1} \tag{1.15}\] La varianza mide la dispersión de todas las observaciones respecto de la media, es decir, cómo de alejadas o cercanas se encuentran las observaciones respecto de la media. Cuanto mayor sea la varianza, mayor será la dispersión y en consecuencia más heterogéneos serán los datos de la variable y menos representativa su media.

Ejemplo 1.18 La eficiencia productiva (en puntos porcentuales) de una muestra de 5 empresas es:

50, 72, 70, 78, 95

Calcular la eficiencia productiva media y su varianza.

Solución: La variable objeto de estudio es X=“Eficiencia productiva (en puntos porcentuales)”.

Creamos una tabla para facilitar los cálculos (Tabla 1.14). Para ello, comenzamos disponiendo los datos ordenados de menor a mayor (columna 1). A partir de los datos de la columna 1 podemos calcular la eficiencia media: \[\bar{x}=\frac{\displaystyle\sum_{i=1}^{n=5}x_i }{n}=\frac{x_1+x_2+...+x_{5}}{5}=\frac{50+70+72+78+90}{5}=\frac{365}{5}=73\text{ (puntos porcentuales)}\] Para calcular la varianza según la Ecuación 1.15 necesitamos calcular el numerador: $(x_i-\bar{x})^2$. Así pues, a partir de la media podemos calcular las columnas $x_i-\bar{x}$ (columna 2 = columna 1 - 73) y $(x_i-\bar{x})^2$ (columna 3 = cuadrado de columna 2).

Tabla 1.14: Tabla para el cálculo de la varianza con frecuencias unitarias (Ejemplo 1.18)

$x_i$	$x_i-\bar{x}$	$(x_i-\bar{x})^2$
50	-23	529
70	-3	9
72	-1	1
78	5	25
95	22	484
——	—–	—–
$\sum=365$	$\sum=0$	$\sum=1,048$

Sumando la columna 3 de la Tabla 1.14 tendremos el numerador de la expresión de la varianza.

Por tanto: \[{S_X^2}=\frac{ \displaystyle\sum_{i=1}^{n=5}\left (x_i - \bar{x} \right )^2 }{n-1} = \frac{529+9+1+25+484}{5-1}=\frac{1,048}{4}=262\text{ (puntos porcentuales)}^2\]

Ejemplo 1.18. con Excel. Para calcular la varianza de la eficiencia podemos:

Opción 1. Reproducir los cálculos que se muestran en la Tabla 1.14. Esto se trataría de un ejercicio teórico porque tenemos funciones en Excel para calcular la varianza.

Con la finalidad de practicar, vamos a resolver el cálculo de la varianza de las dos formas que hemos planteado.

Escribimos en la celda:
- A1: eficiencia $\hspace{2.5cm}\text{para representar ---> }x_i$
- B1: eficiencia-media $\hspace{1.45cm}\text{para representar ---> }x_i-\bar{x}$
- C1: (eficiencia-media)^2 $\hspace{0.8cm}\text{para representar ---> }(x_i-\bar{x})^2$
- A8: n
- A9: media
- A10: varianza-op1
- A11: varianza-op2
En el rango A2:A6 introducimos los datos observados de eficiencia.

En la celda B8 calculamos el tamaño de la muestra. Está claro que $n$ es 5, pero si tuviesemos más casos no sería tan inmediato. Para saber cuánto es $n$ utilizamos la función CONTAR(), que cuenta el número de celdas de un rango que contiene valores numéricos.

En la celda B9 calculamos la media de eficiencia. Para ello, ejecutamos en esta celda la fórmula: =promedio(A2:A6). En la celda B2 escribimos la fórmula: =A1-$B$9. Lo que está haciendo esta celda es calcular la diferencia entre el valor de la eficiencia y la media. Como después arrastraremos esta celda para copiarla, se ha fijado la celda B4. Por último, en la celda C2 escribimos la fórmula: B2^2, para calcular el cuadrado de la celda B2.

A continuación, seleccionamos el rango B2:C2 y arrastramos hasta la fila 7 para copiar las fórmulas que hemos introducido para el primera caso.

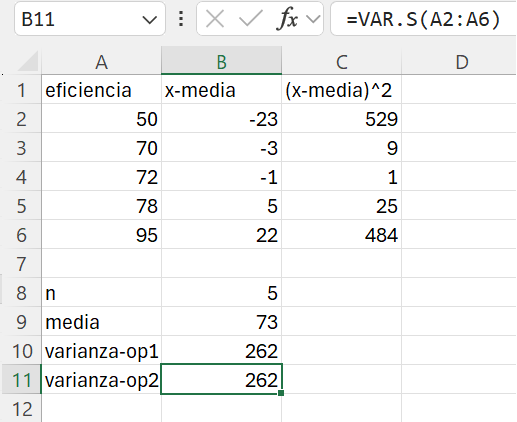
Vamos a la celda B10 y, como indica la expresión de la varianza muestra (Ecuación 1.15), sumamos el rango C2:C6 y lo dividimos por $n$ menos 1. En consecuencia, en la celda B10 escribimos: =suma(C2:C6)/(B8-1). Al ejecutar la fórmula obtenemos que la varianza muestral es 262.
Opción 2. Sería la opción más real. Sin embargo, tenemos que saber que disponemos de dos funciones en Excel para calcular la varianza, son:
- VAR.P(): calcula la varianza de la población; por tanto aplica la Ecuación 1.17
- VAR.S(): calcula la varianza de una muestra. En este caso Excel hace uso de la Ecuación 1.15.
Entonces, siempre tenemos que saber si los datos que estamos analizando corresponden a una muestra o a la población. En este ejercicio, está claro que se trata de una muestra de 5 empresas. Dicho esto, en la celda B11 escribimos y ejecutamos la siguiente fórmula: =var.s(A2:A6). El resultado será el ya conocido, la varianza muestra es 262. El resultado final debería ser similar al que se muestra en la Figura 1.20.

Figura 1.20: Resolución del ejemplo 1.18. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_18.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_18_excel.gif](https://www.uv.es/ticstat/ej_1_18_excel.gif) encontrarás cómo distintas formas de calcular la varianza.

Los manuales de estadística anglosajones y los softwares estadísticos (R, SPSS, STATA, Minitab, etc.) se refieren a la varianza muestral con la fórmula dada en la Ecuación 1.15. Sin embargo, la mayoría de manuales españoles cuando se refieren a la varianza muestral utilizan la expresión: \[{S_X^{2}}=\frac{ \displaystyle\sum_{i=1}^{n}\left (x_i - \bar{x} \right )^2 }{n}\]

Si hemos resumido los valores de la variable en una tabla de frecuencias, la varianza muestral se expresa como: \[ {S_X^2}=\frac{ \displaystyle\sum_{i=1}^{I}\left (x_i - \bar{x} \right )^2 \cdot n_i }{n-1} \tag{1.16}\]

Ejemplo 1.19 En el Ejemplo 1.8 calculamos que la experiencia media de una muestra de 15 empleados de una empresa se situaba en 3.2 años. Partiendo de la tabla estadística ampliada construida en aquel ejemplo (Tabla 1.15), ahora vamos a calcular la varianza de la experiencia utilizando la Ecuación 1.16.

Nota: Calculamos la varianza muestral porque tenemos una seleccion/muestra de trabajadores.

Tabla 1.15: Tabla inicial para el cálculo de la varianza a partir de la tabla de frecuencias.

$x_i$	$n_i$	$x_i \cdot n_i$
1	1	1
2	3	6
3	5	15
4	4	16
5	2	10
	—–	—–
	$n=15$	$\sum=48$

Solución: Como sabemos que la media de la experiencia es 3.2 años, añadimos una columna a la Tabla 1.15 que recoja la diferencia entre los valores de la variable y su media; sin embargo, como ahora los valores de la variable se repiten, las desviaciones calculadas tenemos que multiplicarlas por las frecuencias (columna 5). Por último, para obtener el numerador de la varianza muestral en la Ecuación 1.16, el resultado de la columna 5 la tenemos que multiplicar por la columna 4 para obtener el cuadrado de las desviaciones de los valores de la variable respecto de su media (columna 6). Todos estos cálculos se muestran en la Tabla 1.16.

Tabla 1.16: Tabla para el cálculo de la varianza (Ejemplo 1.19).

$x_i$	$n_i$	$x_i \cdot n_i$	$x_i - \bar{x}$	$(x_i - \bar{x}) \cdot n_i$	$(x_i - \bar{x})^2 \cdot n_i$
1	1	1	-2.2	-2.2	4.84
2	3	6	-1.2	-3.6	4.32
3	5	15	-0.2	-1	0.2
4	4	16	0.8	3.2	2.56
5	2	10	1.8	3.6	6.48
	—	—		—	—
	$n=15$	$\sum=48$		$\sum=0$	$\sum=18.4$

Ahora, si sumamos la columna 6 tenemos que: $\displaystyle\sum_{i=1}^{I=5}(x_i - \bar{x})^2 \cdot n_i=18.4$. A partir de este resultado podemos calcular la varianza muestral. \[{S_X^2}=\frac{ \displaystyle\sum_{i=1}^{I=5}\left (x_i - \bar{x} \right )^2 \cdot n_i}{n-1} = \frac{18.4}{15-1}=1.3143\text{ años}^2\]

Ejemplo 1.19. con Excel. Cuando los datos se encuentran agregados en una tabla estadística no podemos utilizar ninguna función de Excel para calcular la varianza. En estos casos tenemos que reproducir los cálculos, como se ha hecho en el Ejemplo 1.19. Podemos ahorrarnos algunos pasos utilizando la función SUMAPRODUCTO() (Nota: Esta forma de resolver se pide en el Ejercicio 1.12.

Abrimos un nuevo libro de Excel.

En el rango A1:F1 escribimos los nombres de las cabeceras de las columnas. Por ejemplo:

A1: xi
B1: ni
C1: xini
D1: x-media $\hspace{1.65cm}\text{para representar ---> }x_i-\bar{x}$
E1: (x-media)*ni $\hspace{0.95cm}\text{para representar ---> }(x_i-\bar{x}) \cdot n_i$
F1: (x-media)^2*ni $\hspace{0.6cm}\text{para representar ---> }(x_i-\bar{x})^2 \cdot n_i$

También escribimos en las celdas:

A8: n
A9: media
A10: varianza

En el rango A2:B6 introducimos los datos del Ejemplo 1.9.

En la celda B8 sumamos el rango B2:B6 para obtener el tamaño de la muestra.

En la celda C2 multiplicamos las celdas A2 y B2. Ejecutamos y arrastramos hasta C6 para copiar el contenido.

Calculamos la media en la celda B9 sumando el rango C2:C6 y dividiendo por el tamaño de la muestra (celda B8).

En la celda D2 calculamos la deviación del valor de la eficiencia para ese caso respecto de la media, es decir, queremos obtener: $(x_i-\bar{x})$. Para ello, en la celda introducimos al fórmula: =A2-$B$9. Mantenmos fija la celda B9 para que no cambie cuando arrastremos la celda D2 para copiar la fórmula.

Ahora, en la celda E2 multiplicamos C2 por B2 para obtener $(x_i-\bar{x_i}) \cdot n_i$); y en la celda F2 multiplicamos E2 por D2 para tener $(x_i-\bar{x})^2 \cdot n_i$.

Seleccionamos el rango D2:F6 y arrastramos hacia abajo hasta la fila 6 para copiar las fórmulas en este rango.

Finalmente, en la celda B10 sumamos el rango F2:F6 y lo dividimos entre el tamaño de la muestra (celda B8) menos 1. La varainza nos da aproximadamente 1.3143

El resultado final debería ser similar al que se muestra en la Figura 1.21.

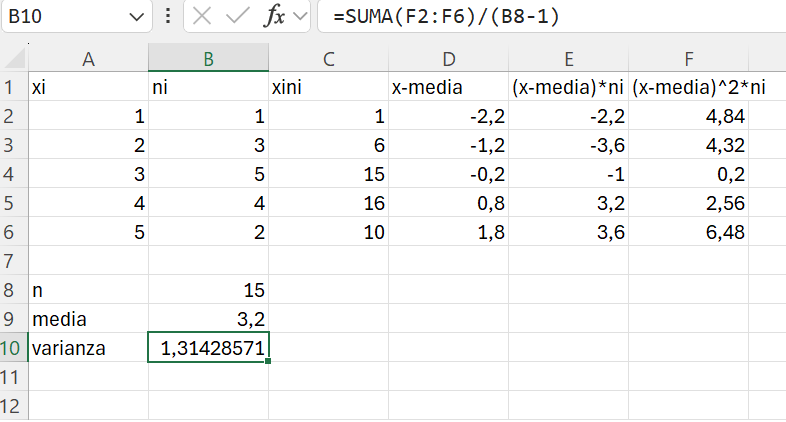
Figura 1.21: Resolución del ejemplo 1.19. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_19.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_19_excel.gif](https://www.uv.es/ticstat/ej_1_19_excel.gif) encontrarás cómo se ha calculado la varianza en este ejemplo.

Si la varianza de una variable es alta, existe mucha dispersión, los valores de la variable se encuentran alejados de la media y, por tanto, está no será representativa del conjunto de datos. Lo opuesto si la varianza es pequeña. Sin embargo, como la varianza no está expresada en las mismas unidades de medida que la variable original es difícil interpretar su resultado. Por esto, la medida de dispersión absoluta que se suele calcular y con la que se acompaña a la media es la desviación típica.

La varianza de la población se denota por $\sigma^2$ y se expresa como: \[ {\sigma_X^2}=\frac{\displaystyle\sum_{i=1}^{N}\left (x_i-\mu_{x}\right)^2}{N} \tag{1.17}\] alternativamente, si los datos están dispuestos en una tabla de frecuencias: \[{\sigma_X^2}=\frac{\displaystyle\sum_{i=1}^{I}\left (x_i-\mu_{x}\right)^2 \cdot n_i}{N} \tag{1.18}\]

1.5.3.1 Propiedades de la varianza

La varianza presenta las siguientes propiedades:

La varianza siempre es positiva: $S^2>0$. La varianza sólo será cero si todos los valores de la variable son iguales, es decir, es una constante.
La presencia de valores extremos o anómalos afecta a la varianza.
La varianza viene expresada en las unidades de medida de la variable al cuadrado.
La varianza es invariante a los cambios de origen pero depende de los cambios de escala al cuadrado.

Tenemos que tener muy claro si estamos calculando la varianza de una muestra o la varianza de la población.

1.5.4 Desviación típica

La desviación típica muestral (se denota por $S$) es la raíz cuadrada de la varianza muestral.\[S_X=+ \sqrt{S_X^2}= + \sqrt{\frac{ \displaystyle\sum_{i=1}^{n}\left (x_i - \bar{x} \right )^2 }{n-1}} \tag{1.19}\] o alternativamente, considerando frecuencias no unitarias,\[S_X=+ \sqrt{S_X^2}= + \sqrt{\frac{ \displaystyle\sum_{i=1}^{I}\left (x_i - \bar{x} \right )^2\cdot n_i }{n-1}} \tag{1.20}\] A diferencia de la varianza, la desviación típica viene expresada en las mismas unidades de medida que la variable.

Los manuales de estadística anglosajones y los softwares estadísticos (R, SPSS, STATA, Minitab, etc.) se refieren a la desviación muestral con la fórmula dada en la Ecuación 1.19 o Ecuación 1.20. Sin embargo, la mayoría de manuales españoles cuando se refieren a la desviación típica muestral utilizan la expresión: \[S_X=\sqrt{\frac{ \displaystyle\sum_{i=1}^{I}\left (x_i - \bar{x} \right )^2\cdot n_i }{n}}\]

Ejemplo 1.20 Obtener la desviación típica muestral de la experiencia de los empleados.

Solución: En el Ejemplo 1.19 hemos calculado la varianza muestral de la experiencia de los empleados. La desviación típica muestral es la raíz cuadrada de la varianza, por tanto:
\[S_X=\sqrt{S_X^2}=\sqrt{1.3143}=1.1464 \hspace{2mm}\text{años}\]

Ejemplo 1.20. con Excel. Como sucede con la varianza, tenemos dos fórmulas en Excel para calcular la desviación típica:

DESVEST.P(): calcula la desviación típica (o estándar) de la población; por tanto aplica la Ecuación 1.21.
DESVEST.M(): calcula la desviación típica (o estándar) de una muestra. En este caso Excel hace uso de la Ecuación 1.19.

Estas funciones podemos utilizarlas si los datos no están agrupados en una tabla de frecuencias. Si así fuera, debemos proceder como se ha comentado en la opción 1 del ejercicio 1.19 con Excel, es decir, realizar los pasos intermedios para calcular la varianza, y luego obtener la desvación típica calculando la raíz cuadrada (se hace con la función RAIZ()).

Vamos a calcular de desviación típica de la experiencia. Abrimos el fichero ej_1_17.xlsx.

En el rango C9:C10 escribimos, respectivamente, varianza y desviación. Nos situamos en la celda D9 e introducimos la fórmula: =var.s(A2:A16); en la celda D10 escribimos y ejecutamos la fórmula: =desvest.m(A2:A16). Alternativamente, en la celda E10 calcularemos la desviación típica como la raiz cuadrada de la varianza; para ello, ejecutamos la fórmula: =raiz(D9).

Obtenemos como resultados que la varianza de la experiencia es 1.3143 (años$^2$) y la desviación típica es 1.1464 años.

El resultado final debería ser similar al que se muestra en la Figura 1.22.

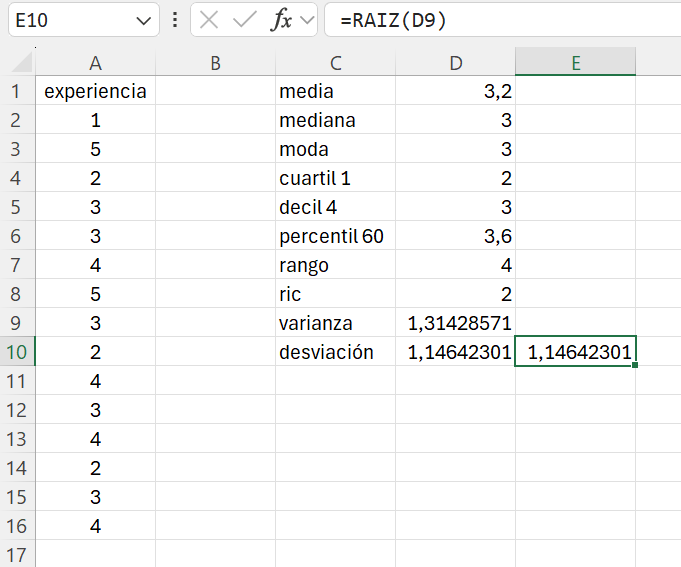
Figura 1.22: Resolución del ejemplo 1.20. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_20.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_20_excel.gif](https://www.uv.es/ticstat/ej_1_20_excel.gif) encontrarás cómo se ha calculado la desviación típica en este ejemplo.

La desviación típica poblacional se denota por $\sigma$ y se calcula por medio de esta expresión:\[ {\sigma_X}=\sqrt{\frac{\displaystyle\sum_{i=1}^{N}\left (x_i-\mu_{x}\right)^2}{N}} \tag{1.21}\] Alternativamente, si los datos están dispuestos en una tabla de frecuencias:\[{\sigma_X}=\sqrt{\frac{\displaystyle\sum_{i=1}^{I}\left (x_i-\mu_{x}\right)^2 \cdot n_i}{N}} \tag{1.22}\]

A partir de ahora me referiré a la varianza o la desviación típica tal y como la he definido en este manual. Que me refiera a la varianza muestral o poblacional dependerá de si estamos trabajando con una muestra o con la población.

Insistir nuevamente en que siempre tenemos que tener presente si los datos con los que trabajamos son una muestra o se refieren a la población (¡a todos!).

1.5.5 Coeficiente de variación

El coeficiente de variación muestral (de Pearson) se denota por $g_0$ y se define como: \[\begin{equation} g_{0_X}=\frac{S_X}{\bar{x}} (\#eq:coef-variacion) \end{equation}\]

es decir, el coeficiente de variación relaciona la desviación típica con la media.

Si la media de la variable objeto de estudio es negativa, entonces el coeficiente de variación se calcula a partir del valor absoluto de la media, es decir, según la expresión:

\[\begin{equation} g_{0_X}=\frac{S_X}{|\bar{x}|} (\#eq:coef-variacion2) \end{equation}\]

porque en el caso de que la media de una variable tome el valor $0$, como sucede con las variables tipificadas (ver @ref(tipificacion)), el coeficiente de variación sería $\infty$. Es más, autores como Montiel, Rius y Barón recomiendan no usar el coeficiente de variación en aquellos casos en los que no se puede asegurar que la media de la variable es positiva (A. M. Montiel (1996)).

Si la desviación típica es grande la dispersión será grande. El problema es determinar qué significa en este contexto grande. Sin embargo, como el coeficiente de variación nos está indicando cuántas veces está contenida la desviación típica en la media, cuanto mayor sea el coeficiente de variación mayor será la dispersión relativa.

Es frecuente expresar $g_0$ en porcentaje, indicando el porcentaje que representa la desviación típica respecto de la media.

Según Casas-Sánchez y Santos-Peñas (1995), cuanto más se aproxime el coeficiente de variación a la unidad mayor será la dispersión en los datos observados y peor será la representatividad de la media. A partir de la unidad la media no representará bien como medida de tendencia central al conjunto de datos.

El coeficiente de variación es una medida de dispersión relativa y se utiliza fundamentalmente para dar respuesta a dos tipos preguntas:

¿Es representativa la media que hemos calculado de una variable?

Respuesta: Cuanto mayor sea $g_0$, mayor será la dipersión y, por tanto, menor será la representatividad de la media. Suele utilizarse como criterio para considerar que la media es representativa el que $g_0$ sea menor a 1, y será más representativa cuanto menor sea $g_0$.
Al comparar dos o más variables (o distribuciones de frecuencias), ¿cuál presenta una mayor/menor dispersión o variabilidad?

Respuesta: Como el coeficiente de variación es una medida adimensional podemos utilizarlo para comparar la dispersión de dos o más variables. La variable con menor dispersión será aquella que tenga un menor coeficiente de variación.

El coeficiente de variación no resulta útil si la media toma un valor próximo a cero, el coeficiente tiende a infinito.

El coeficiente de variación poblacional se denota por $\gamma_0$ y tiene la siguiente expresión:\[\gamma_{0}=\frac{\sigma}{\mu}\]

Ejemplo 1.21 Del estudio de la distribución de los salarios de dos empresas A y B de un mismo sector se han obtenido los siguientes resultados: el salario medio mensual en la empresa A es de 1,100 euros con una desviación típica de 150 euros, y el salario medio de la empresa B es de 1,200 euros con una varianza de 40,000 $euros^2$.

¿En cuál de las dos empresas el salario presenta una menor dispersión relativa? Razona la respuesta.

Solución: La variable objeto de estudio es el salario mensual (en euros). Tenemos que analizar qué empresa presenta una menor dispersión o variabilidad en el salario. No podemos considerar que la empresa con menor dispersión será aquella con menor varianza o desviación típica porque las medias salariales sobre las que se calculan estas medidas estadísticas son distintas. Por tanto, para poder comparar la dispersión salarial tenemos que acudir al coeficiente de variación (de Pearson).

La variable X se define como: “Salario mensual (en euros) en la empresa A”; y la variable Y como: “Salario mensual (en euros) en la empresa B”.

Calculamos los correspondientes coeficientes de variación para poder comparar la variabilidad/dispersión de los salarios de las dos empresas. \[\begin{matrix} g_{0_X}=\frac{S_X}{\bar{x}}=\frac{150}{1,100}=0.1364 \\ \\ g_{0_Y}=\frac{S_y}{\bar{y}}=\frac{\sqrt{40,000}}{1,200}=\frac{200}{1,200}=0.1667 \end{matrix}\]

El coeficiente de variación del salario mensual en la empresa A es de 0.1367, mientras que en la empresa B es de 0.1667. En ambos casos la dispersión salarial es baja - el coeficiente de variación es pequeño (menor que 0.3)-, pero es ligeramente menor en la empresa A.

No hay una función en Excel para calcular el coeficiente de variación.

1.6 Medidas de forma

Las medidas de forma permiten hacernos una idea de cómo es la forma de la distribución de una variable. Si es simétrica o asimétrica (coeficiente de asimetría: coeficiente de Fisher, coeficiente de Pearson, coeficiente de Bowley-Yule, etc.); y/o si es más o menos apuntada que la distribución normal (coeficiente de apuntamiento: coeficiente de Curtosis, coeficiente de Kelly, etc.).

En este apartado haremos referencia al coeficiente de asimetría de Fisher y al coeficiente de Curtosis.

No es habitual practicar el cálculo del coeficiente de asimetría y de curtosis a mano, no porque sea complicado, sino porque requiere mucho cálculo y resulta tedioso.

1.6.1 Coeficiente de asimetría

La distribución de frecuencias de una variable es simétrica respecto a la media cuando las observaciones (valores) localizadas a la misma distancia de la media (tanto por encima como por debajo) tienen la misma frecuencia. La representación gráfica de una distribución simétrica con forma campaniforme se muestra en la gráfica izquierda de la Figura 1.23; y para una distribución simétrica en forma de U en la gráfica derecha de la misma Figura.

Si la distribución de la variable presenta (muchos) más valores a la izquierda (por encima) de la media, la distribución es asimétrica negativa. En cambio, si los valores se localizan mayoritariamente a la derecha (por debajo) de la media, la distribución es asimétrica positiva.

La medida estadística mas comúnmente utilizada para medir la simetría de una variable es el denominado coeficiente de asimetría de Fisher, que se denota por $g_1$ y se define como:\[ g_1 = \frac{\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^3}{n}}{S^3_X} \tag{1.23}\] y si partimos de la distribución de frecuencias:\[g_1 = \frac{\frac{\displaystyle\sum_{i=1}^I(x_i-\bar{x})^3 \cdot n_i}{n}}{S^3_X} \tag{1.24}\] Si observamos el numerador del coeficiente de asimetría, las desviaciones de los valores de la variable respecto a la media se encuentran elevadas a 3. La razón de elevar a 3 es que se mantenga el signo de la suma de desviaciones ($x_i-\bar{x}$). Si la distribución es simétrica, la suma de estas desviaciones será cero. Por otra lado, la media de las desviaciones cúbicas (numerador de $g_1$) se divide por la desviación típica elevado a 3 para hacer que el coeficiente de asimetría sea adimensional (no dependa de los cambios de escala o unidad). De esta forma, puede utilizarse $g_1$ para comparar la simetría/asimetría entre variables.

Entonces, ¿cómo interpretar el valor obtenido del coeficiente de simetría?

Si $g_1=0$, la distribución de la variable es simétrica. La suma de las desviaciones es cero y, por tanto, el coeficiente $g_1$ será cero.

En una distribución simétrica, el valor de la media y la mediana coinciden ($\bar{x}=Me=4$). Si la distribución además es campaniforme, media, mediana y moda coinciden. Esto lo podemos ver en Figura Figura 1.23, gráfica de la izquierda, en la que ($\bar{x}=Me=Mo=4$). Sin embargo, la distribución con forma de U es simétrica y bimodal ($Mo=1$ y $Mo=7$).

En el caso de que obtengamos un coeficiente de asimetría positivo ($g_1>0$), la distribución de la variable se dice que es asimétrica positiva. Las desviaciones ($x_i-\bar{x}$) positivas son mayores que las negativas, obteniéndose un valor positivo del coeficiente de asimetría. Gráficamente veríamos que la distribución de la variable presenta una cola a la derecha. En la Figura 1.24, gráfica de la izquierda, se ha situado el valor de media ($\bar{x}=2.5$, línea de color rojo) y de la mediana ($Me=2$, línea de color azul).

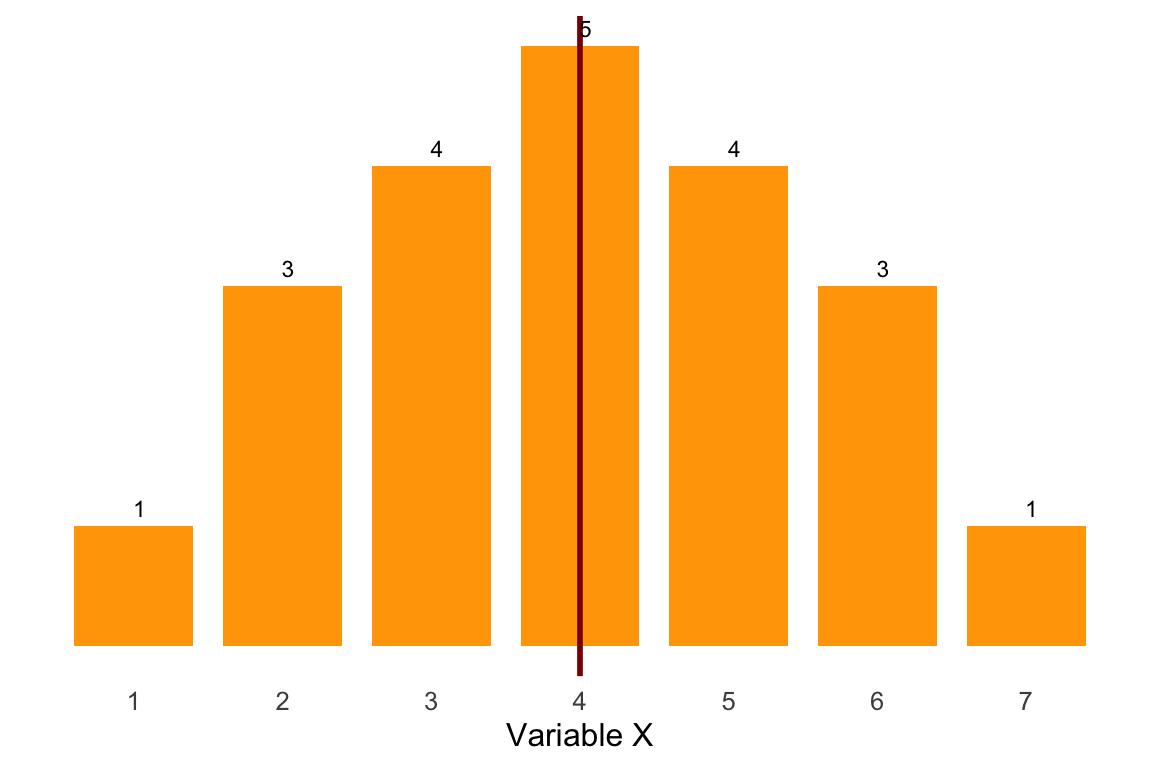
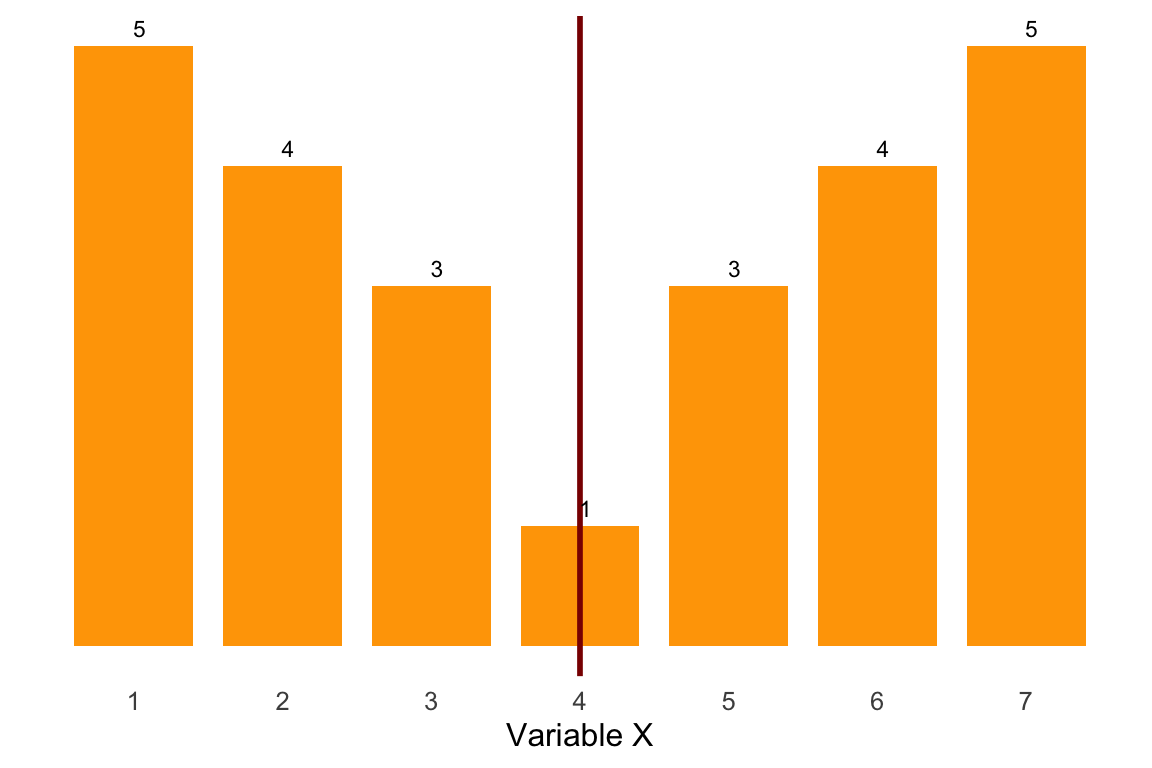
Finalmente, si $g_1<0$, diremos que la distribución de la variable es asimétrica negativa. En este caso, las desviaciones ($x_i-\bar{x}$) negativas son mayores que las positivas, haciendo que el coeficiente de asimetría tome valores negativos. Gráficamente veríamos que la distribución de la variable presenta una cola a la izquierda. En la gráfica derecha de la Figura 1.24 se ha situado el valor de media ($\bar{x}=4.5$, línea de color rojo) y de la mediana ($Me=5$, línea de color azul).

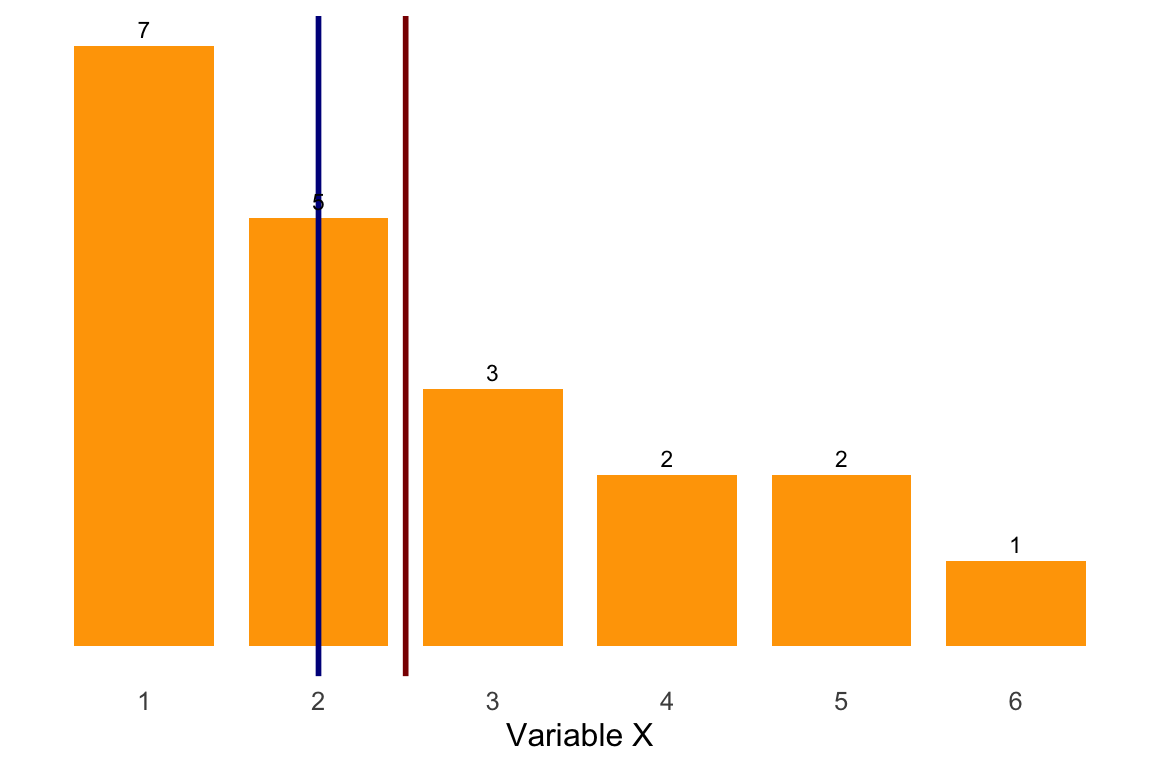
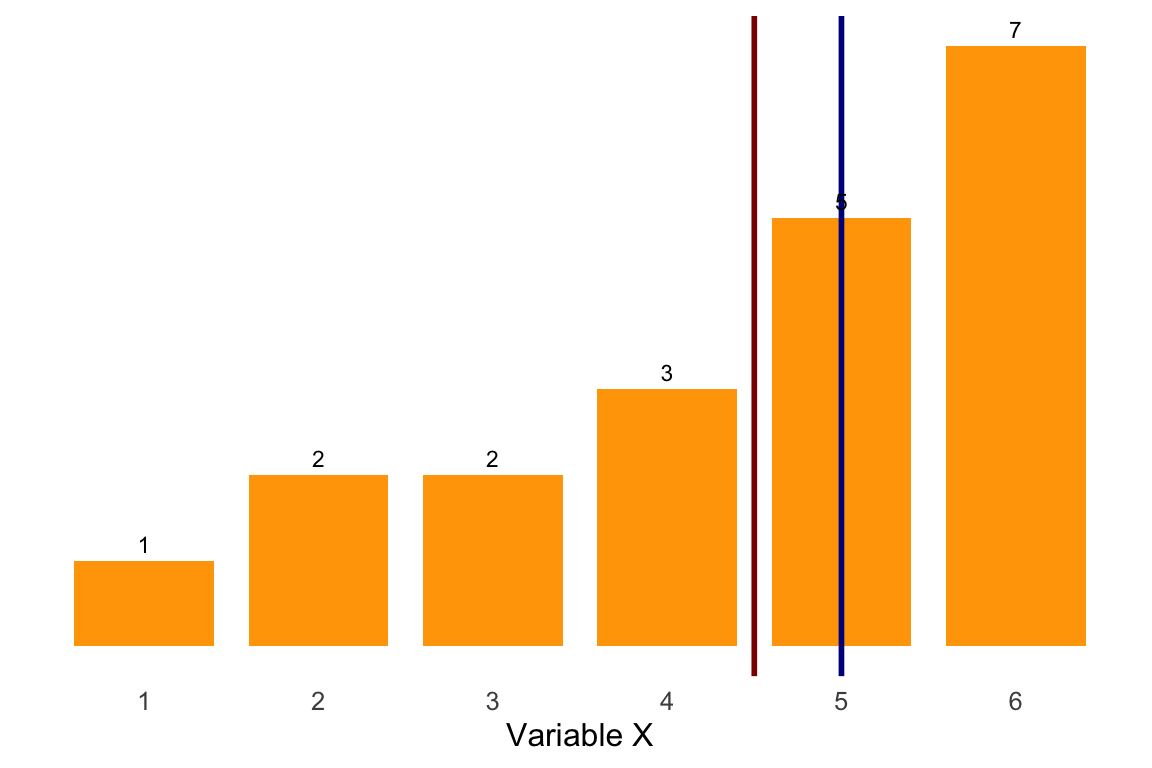
1.6.2 Coeficiente de curtosis

Con el coeficiente de curtosis tratamos de determinar lo apuntada o achatada que es la distribución de frecuencias de una variable. Si la mayor parte de las observaciones/valores de la variable se sitúan alrededor de la media, la distribución será muy apuntada. Por el contrario, si existe mucha variabilidad y las observaciones de alejan de la media, tanto por encima como por debajo, la distribución será muy achatada.

El coeficiente de curtosis se denota por $g_2$ y se define como:\[g_2 = \frac{\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^4}{n}}{S^4_X} - 3 \tag{1.25}\] y si partimos de la distribución de frecuencias:\[g_2 = \frac{\frac{\displaystyle\sum_{i=1}^I(x_i-\bar{x})^4 \cdot n_i}{n}}{S^4_X} - 3 \tag{1.26}\]

Para referirnos, en general, al grado de apuntamiento de una variable se toma como referencia la distribución normal, que presenta un coeficiente de curtosis de 3. De tal forma que si:

$g_2=0$, la distribución es igual de apuntada que la distribución normal (en la Figura 1.25, curva en color rojo).
$g_2>0$, la distribución es más apuntada que la distribución normal (en la Figura 1.25, curva en color azul).
$g_2<0$, la distribución es menos apuntada que la distribución normal (en la Figura 1.25, curva en colo verde).

La distribución normal tiene un coeficiente de curtosis igual a 3. Por esta razón, también es frecuente expresar el coeficiente de curtosis como:\[ g_2 = \frac{\frac{\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^4}{n}}{S^4_X} \tag{1.27}\] es decir, no le restamos el 3. En este caso:

$g_2 = 3$, la distribución es igual de apuntada que la distribución normal (en la Figura 1.25, curva en color rojo).
$g_{2} > 3$, la distribución es más apuntada que la distribución normal (en la Figura 1.25), curva en color azul).
$g_{2} < 3$, la distribución es menos apuntada que la distribución normal (en la Figura 1.25, curva en colo verde).

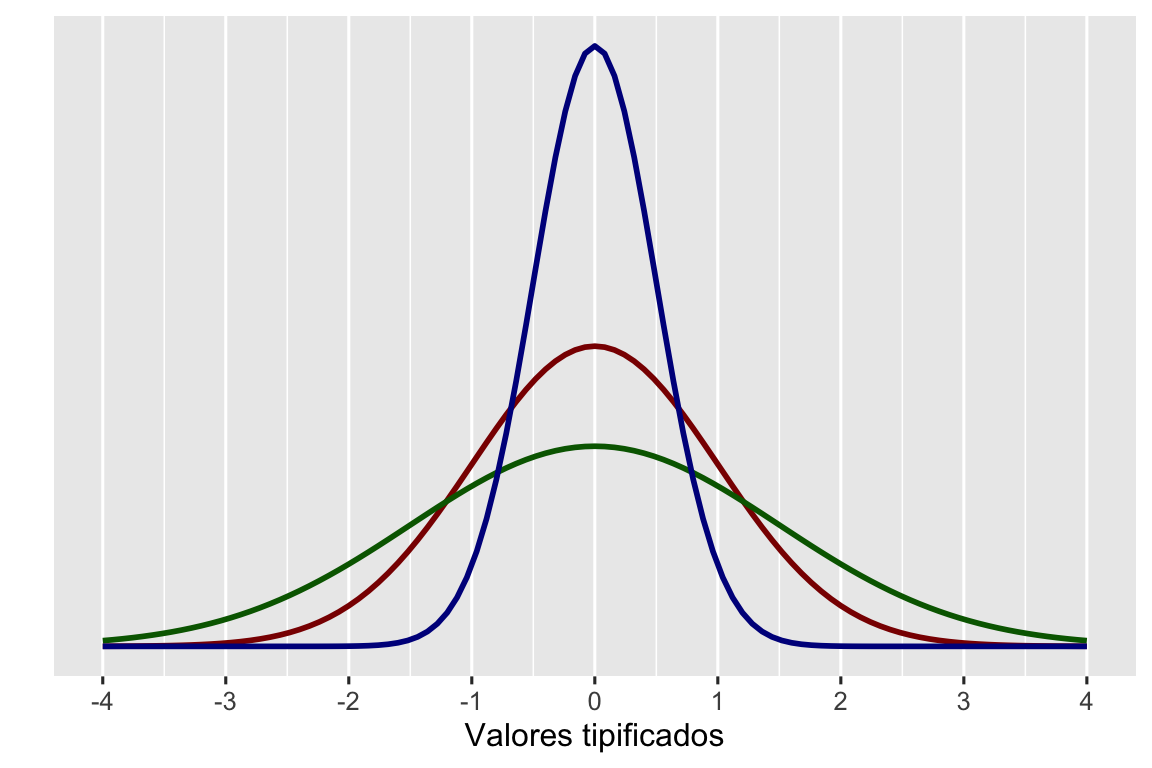
Figura 1.25: Apuntamiento (Curtosis) en la distribución normal

Los coeficientes de asimetría y curtosis poblacionales se denotan por $\gamma_{1}$ y $\gamma_{2}$, respectivamente; sus expresiones son: \[\gamma_{1_X}= \frac{\frac{\displaystyle\sum_{i=1}^{n}(x_i-\mu_{x})^3}{n}}{\sigma^3_X} \tag{1.28}\]\[ \gamma_{2_X}= \frac{\frac{\displaystyle\sum_{i=1}^{n}(x_i-\mu_{x})^4}{n}}{\sigma^4_X} - 3 \tag{1.29}\]

Ejemplo 1.22 Para el número de siniestros reportados por una muestra de 10 hogares se ha calculado el grado de apuntamiento según la Ecuación 1.26, obteniéndose un valor de -0.5. Interpreta este resultado.

Solución: Como el coeficiente de curtosis es -0.5 podemos decir que la distribución de los siniestros reportados por los hogares es ligeramente platicúrtica, es decir, menos apuntada que la normal.

Ejemplo 1.22 con Excel. No vamos a calcular a mano los coeficientes de asimetria y curtosis. Más que los cálculos en este caso lo que interesa es la interpretación. Voy a plantear formas alternativas de calcular los coeficientes de asimetría y curtosis en función de si los datos los tenemos agregados en una tabla estadística o no.

Si tenemos los datos en una tabla, como en el Ejemplo 1.19, tenemos que realizar los pasos intermedios para calcular los coeficientes. Como en el ejemplo 1.19 con Excel calculamos la varianza, vamos a continuar con este ejemplo. Abrimos el fichero ej_1_19.xlsx.

Escribimos en la celda:

G1: (x-media)^3*ni $\hspace{0.95cm}\text{para representar ---> }(x_i-\bar{x})^3 \cdot n_i$
H1: (x-media)^4*ni $\hspace{0.95cm}\text{para representar ---> }(x_i-\bar{x})^4 \cdot n_i$
A11: desviación
A12: asimetría _ A13 curtosis

En la celda B11 calculamos la desviación típica como raiz cuadrada de la varianza.

El valor de la celda G2 será el producto de F2xD2, y la celda H2 será igual a G2xD2 (o alternativamente, a F2^2).

Seleccionamos el rango G2:F2 y arrastramos hacia abajo para copiar las fórmulas.

Recordemos que el coeficiente de asimetría viene dado por la Ecuación 1.24; por tanto, en la celda B12 insertamos la siguiente fórmula: =(suma(G2:G6)/B8)/B11^3.

Análogamente, el coeficiente de curtosis se expresa como indica la Ecuación 1.26. En consecuencia, en la celda B13 ejecutamos la fórmula: =(suma(H2:H6)/B8)/B10^2.

El coeficiente de asimetría es -0.0956 y el de curtosis de 2.018.

El resultado final debería ser similar al que se muestra en la Figura 1.26.

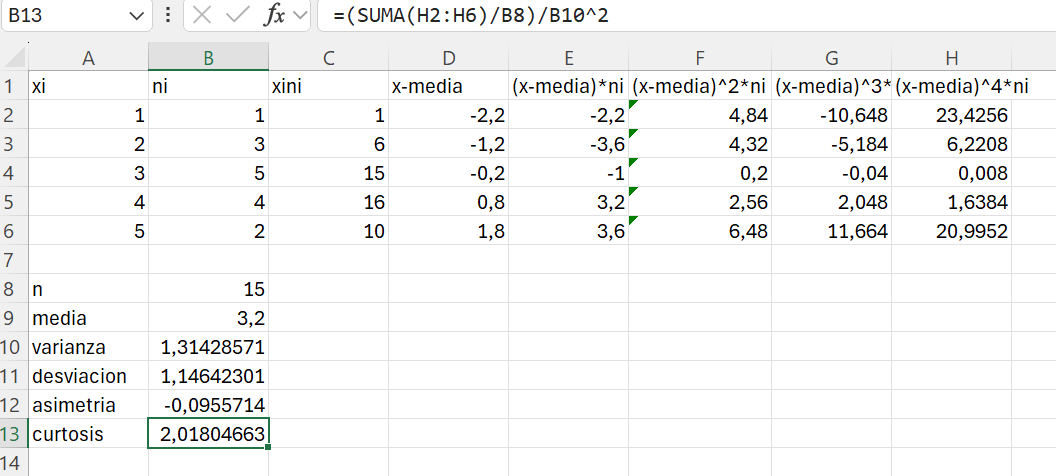
Figura 1.26: Resolución del ejemplo 1.22. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_22.

En la animación que tienes disponible en[https://www.uv.es/ticstat/ej_1_22_excel.gif](https://www.uv.es/ticstat/ej_1_22_excel.gif) encontrarás cómo se ha calculado el coeficiente de asimetría y curtosis.

Si los datos no se encuentran agrupados en una tabla de frecuencias, podemos utilizar las siguientes funciones:

COEFICIENTE.ASIMETRIA(): devuelve la asimetría en una muestra.
COEFICIENTE.ASIMETRIA.P(): devuelve el coeficiente de asimetría poblacional.
CURTOSIS(): devuelve el coeficiente de curtosis.

Abrimos el fichero ej_1_20.xlsx.

En las celdas C11 y C12 escribimos asimetría y curtosis.

En la celda D11 introducimos la fórmula: =coeficiente.asimetria(A2:A16) y en la celda D12: =curtosis(A2:A16).

Como podemos comprobar, los resultados obtenidos con las funciones de Excel son sensiblemente distintos.

Excel y otros softwares como SPSS utilizan otra aproximación para calcular los coeficientes de asimetría y curtosis. Si estás interesado en conocer mas detalles puedes consultar este enlace: https://real-statistics.com/descriptive-statistics/symmetry-skewness-kurtosis/

Más que el cálculo numérico interesa entender la interpretación de la asimetría y curtosis de una distribución/variable.

El resultado final debería ser similar al que se muestra en la Figura 1.27.

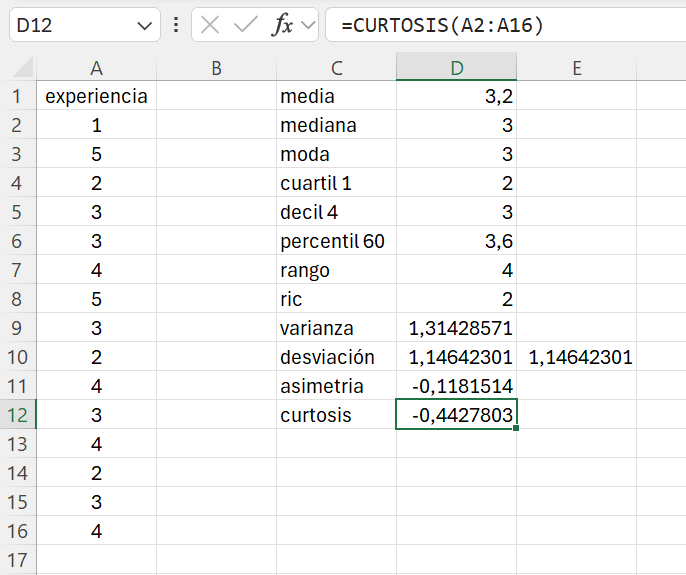
Figura 1.27: Resolución del ejemplo 1.22-2. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_22-2.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_22-2_excel.gif](https://www.uv.es/ticstat/ej_1_22-2_excel.gif) encontrarás cómo se ha calculado el coeficiente de asimetría y curtosis.

1.7 Tipificación de una variable

La variable tipificada $Z$ de una varible $X$ se obtiene a partir de la siguiente transformación:\[ Z=\displaystyle\frac{X-\bar{x}}{S_X} \tag{1.30}\] de forma que los valores tipificados $z_i$ de los valores $x_i$ serán:\[ z_i=\displaystyle\frac{x_i-\bar{x}}{S_X} \tag{1.31}\] Realmente la tipificación supone realizar una transformación lineal en la que el cambio de origen es $a=-\frac{\bar{x}}{S_X}$ y el cambio de escala es $b=\frac{1}{S_X}$. Podemos comprobarlo fácilmente a partir de la Ecuación 1.30: \[Z=\displaystyle\frac{X-\bar{x}}{S_X}=\frac{X}{S_X}-\frac{\bar{x}}{S_X}\]

Como consecuencia de esta transformación, la variable tipificada $Z$ tiene unas propiedades muy importantes:

su media es $\bar{z}=0$
su desviación típica es $S_Z=1$

Cuando tipificamos un valor obtenemos una puntuación relativa que indica el número de desviaciones típicas que ese valor dista de la media de su distribución.

La tipificación puede utilizarse, entre otros casos, para:

Comparar valores de observaciones provenientes de distribuciones en principio no comparables, puesto que los valores tipificados son puntuaciones relativas.
Detectar observaciones anómalas, que tratamos en el apartado Sección 1.8.

Ejemplo 1.23 Considerad el enunciado del Ejemplo 1.21. Si seleccionaramos un trabajador de cada empresa y el trabajador de la empresa A tiene un salario de 1,200 euros y el de la empresa B de 1,350 euros, ¿cuál de los dos trabajadores tiene un mayor salario en términos relativos?

Solución: Del ejemplo Ejemplo 1.21 sabemos que: \[\bar{x}_A=1,100\quad S_{X_A}=150\qquad \qquad \bar{x}_B=1,200\quad S_{X_B}=200\] donde la variable $X$ representa el salario, en euros, de las empresas A y B.

No podemos comparar directamente el salario de los trabajadores seleccionados de las empresas A y B porque proceden de distribuciones distintas, con distintas medias y desviaciones típicas. Para comparar debemos recurrir a una medida relativa; por tanto, vamos a tipificar los salarios de los trabajadores.\[\begin{matrix} z_{x_A}=\displaystyle\frac{x_A-\bar{x}_A}{S_{X_A}}=\frac{1,200-1,100}{150}= 0.67 \\ \\ z_{x_B}=\displaystyle\frac{x_B-\bar{x}_B}{S_{X_B}}=\frac{1,350-1,300}{200}= 0.25 \end{matrix}\] Los salarios de ambos trabajadores se sitúan por encima de sus correspondientes medias (los valores tipificados son positivos). El valor tipificado del salario del trabajador A se sitúa a 0.67 desviaciones típicas de la media ($\bar{z}=0$), mientras que el valor tipificado del trabajador B lo hace a 0.25 desviaciones típicas. En consecuencia, el valor tipificado del trabajador A está más alejado, es decir, su salario relativo es mayor que el del trabajador B.

1.8 Detección de atípicos

Las observaciones atípicas o anómalas son aquellas observaciones que presentan valores extremadamente altos o bajos en comparación con el resto de observaciones, es decir, son observaciones que en principio parecen no ser consistentes con el conjunto de datos. Los valores atípicos o anómalos también reciben el nombre de valores extremos o outliers.

El origen de los valores atípicos puede ser diverso: errores en la recogida de los datos, errores en la medición de los datos, errores en la codificación, errores a la hora de transcribir los datos, se han mezclado datos provenientes de muestras/poblaciones distintas, etc. También están los denominados valores atípicos legítimos, es decir, son valores extremos debido a la variabilidad intrínseca o natural de la característica objeto de estudio.

¿Por qué es importante detectar este tipo de observación/valor?

Tenemos que detectar este tipo de observaciones porque pueden tener una gran influencia en los resultados de nuestros análisis.

Existen distintos criterios para detectar los valores anómalos, pero en este manual vamos a seguir los dos criterios más utilizados en un curso de estadística básica: el criterio de los valores tipificados y el criterio del diagrama de caja y bigotes. Para más detalles sobre los valores atípicos puede consultarse Barnett y Lewis (2008).

Una vez hemos identificado los valores atípicos, la pregunta que debemos formularnos es: ¿qué hacemos con los valores extremos? La respuesta a esta cuestión depende del tipo de valor atípico. Si el origen de la observación atípica es un error nuestro que podemos resolver (por ejemplo, error en la codificación o introducción de los datos) podemos corregir el registro. Si no podemos corregir el error que ha dado lugar al valor anómalo, podemos pensar en eliminar la observación; pero ésta debe ser siempre la última opción. Otra cosa son los atípicos legítimos. En este caso, no debemos eliminar estas observaciones, sino prestarles especial atención en nuestro análisis.

A continuación estudiaremos dos criterios para la detección univariantes de valores atípicos: el criterio de los valores tipificados y la regla de Tukey (Tukey (1977)).

1.8.1 Criterio de los valores tipificados

El teorema o desigualdad de Chebychev, estadístico-matemático ruso, permite determinar la proporción de observaciones que se encuentran entre la media de la distribución y determinada desviación típica. Concretamente, la desigualdad de Chebychev indica para cualquier conjunto de datos, sea cual sea su distribución, el porcentaje de observaciones que se encuentran a k desviaciones típicas de la media es al menos (se trata de una cota mínima) de:\[ 1-\displaystyle\frac{1}{k^2} \tag{1.32}\] siendo $k>1$.

Así, por ejemplo:

Al menos el 75% de observaciones se encuentran dentro de $k=\pm2$ desviaciones típicas respecto de la media.
Al menos el 88% de observaciones se encuentran dentro de $k=\pm3$ desviaciones típicas respecto de la media.

La regla empírica, que únicamente puede aplicarse en el caso de distribuciones de frecuencias simétricas y campaniformes - como la distribución normal- indica que el 68.26% de las observaciones se encontrarían en el intervalo $\bar{x}\pm S_x$; el 95.5% en el intervalo $\bar{x}\pm 2 \cdot S_x$ y el 99.74% en el intervalo $\bar{x}\pm 3 \cdot S_x$. La regla empírica se representa, para los equivalentes valores tipificados, en la Figura 1.28.

Por tanto, como en este tipo de distribución -simétrica, unimodal y campaniforme, como la distribución normal- únicamente el 0.26% de las observaciones son mayores en términos absolutos a 3, estas observaciones se identifican como anómalas.

Bajo el criterio de los valores tipificados, se considera que una observación es atípica si su valor tipificado en términos absolutos es mayor a 3.\[|z_i|>3\quad \rightarrow \quad \text{valor anómalo}\]

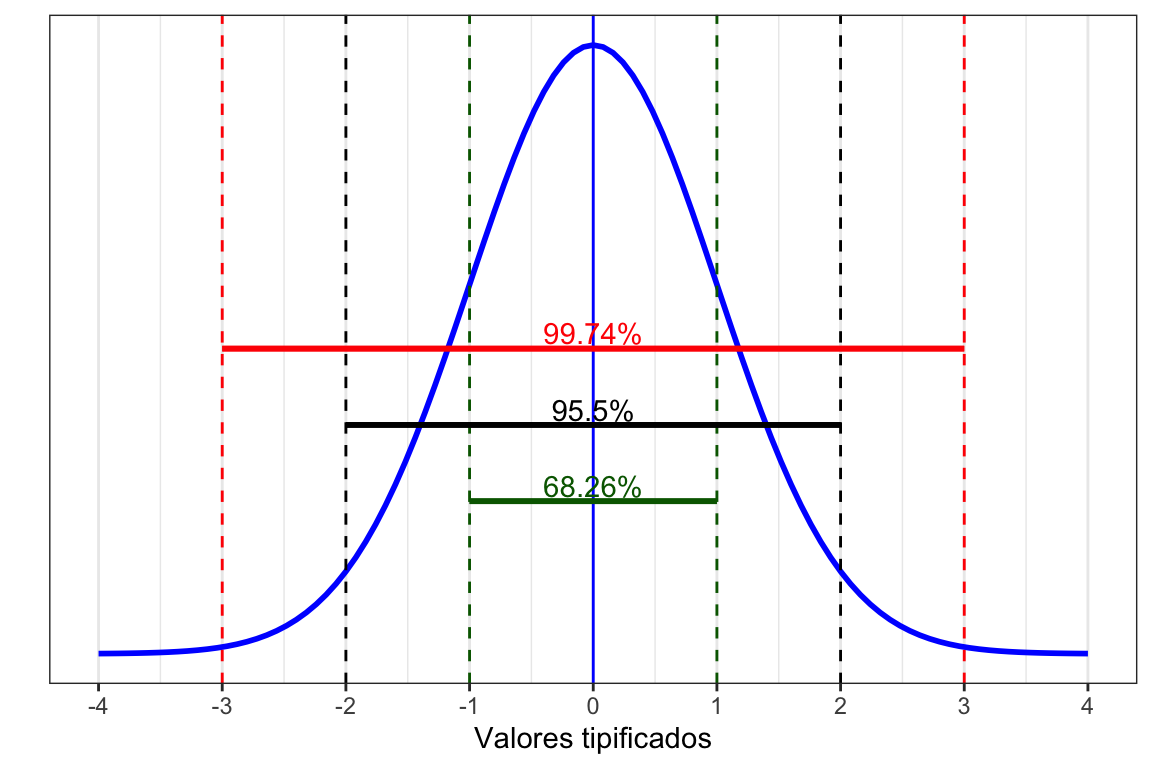
Figura 1.28: Regla empirica aplicada sobre la distribución normal.

Ejemplo 1.23 con Excel. En Excel podemos calcular los valores tipificados utilizando la función NORMALIZACION(). Esta función tiene tres argumentos. En el primer argumento tenemos que identificar el rango o matriz de datos, en el segundo el valor de la media de los datos y en el tercer argumento la desviación típica. En este ejemplo tipificaremos para determinar valores anómalos. La función NORMALIZACION() la podemos utilizar tanto si los datos dispuestos en una tabla de frecuencia como si no, puesto que vamos a tipificar valores individuales.

Abrimos el fichero ej_1_22.xlsx.

En la celda I1 escribimos: valor_tipificado. En la celda I2 insertamos la fórmula: “=normalizacion(A2:A6;$B$9;$B$11). Recuerda, fijamos las celdas donde se encuentra la media y la desviación porque no queremos que estas celdas cambien. Cuando ejecutemos la fórmula de la celda I2 se autocompletará hasta la celda I6. Como vemos, no hay ningún valor anómalo en nuestro conjunto de datos, ningún valor tipicado es mayor a 3, en valor absoluto. No olvides que cada valor tipificado que hemos calculado se repite el mismo número de veces $n_i$ que los valores originales.

El resultado final debería ser similar al que se muestra en la Figura 1.29.

Figura 1.29: Resolución del ejemplo 1.23. con Excel.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_23.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_23_excel.gif](https://www.uv.es/ticstat/ej_1_23_excel.gif) encontrarás cómo se ha calculado el coeficiente de asimetría y curtosis.

1.8.2 Regla de Tukey

La regla de Tukey dice que los valores atípicos son valores que se encuentran situados a más de 1.5 veces el rango intercuartílico, ya sea por debajo de $C_1 - 1.5\cdot RIC$, o por encima de $C_3 + 1.5\cdot RIC$.

El diagrama de caja y bigotes (o boxplot) suele utilizarse para visualizar estos casos atípicos, ya que es una representación gráfica que sitúa la posición de los cuartiles de una distribución y permite visualizar su dispersión y simetría.

Si no estas familizado con el concepto de cuartiles, te recomiendo que consultes el Sección 1.4.5 para que puedas seguir adecuadamente la explicación del diagrama de caja y bigotes.

Como se ilustra en la Figura 1.30, para realizar un diagrama de caja y bigotes se construye una caja rectangular cuya base se obtiene al conectar el valor del primer con el del tercer cuartil, la altura de la caja no es relevante. Dentro de la caja se dibuja una línea vertical que indica la posición de la mediana (o segundo cuartil). Si la mediana está centrada dentro de la caja da idea de una posible simetría; el desplazamiento de la mediana hacia uno de los extremos confirma una asimetría positiva o negativa, según la aproximación sea hacia el extremo inferior o superior de la caja.

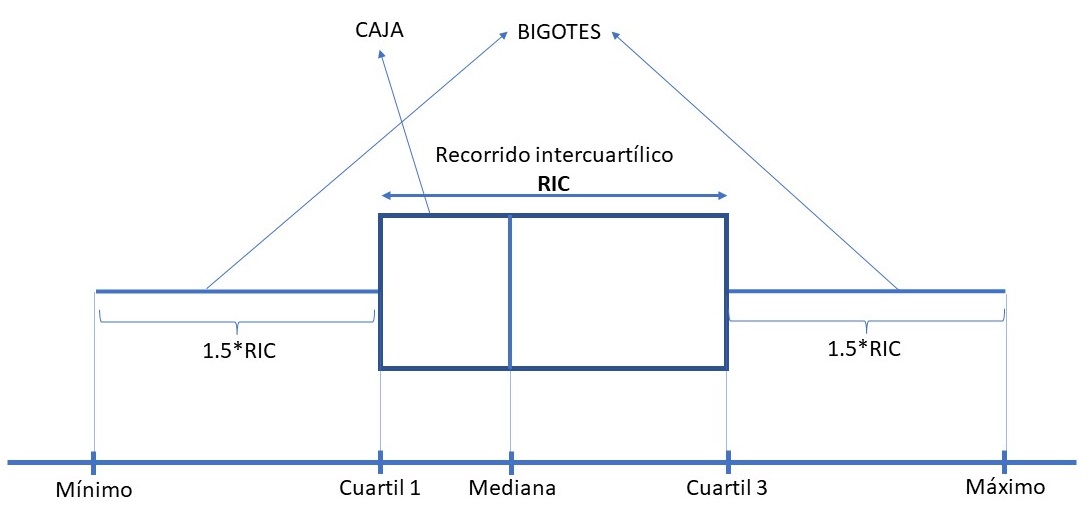
Figura 1.30: Diagrama de caja y bigotes o boxplot.

De la caja se dibujan dos líneas (bigotes), paralelas al eje, cuya longitud máxima será igual a 1.5 veces la diferencia entre el tercer y el primer cuartil (esta diferencia se denomina: recorrido intercuartílico, RIC). Una de las líneas se dibujará desde el primer cuartil hacia el valor mínimo y la otra línea desde el tercer cuartil hacia el valor máximo de la variable. Puede ocurrir que el valor mínimo y/o máximo se sitúe a una distancia menor o igual a 1.5 veces el RIC, en cuyo caso los bigotes se extenderán hasta estos valores.

Sin embargo, también puede ocurrir que el valor mínimo y/o máximo se sitúe, respectivamente, por debajo o por encima de 1.5 veces el RIC. Si es así, todas las observaciones entre los límites de los bigotes y el valor mínimo y/o máximo serán consideradas observaciones atípicas o anómalas.

Las observaciones atípicas o anómalas son todas aquellas que en términos absolutos se encuentran a una distancia mayor a 1.5 veces el recorrido intercuartílico.

Siguiendo la regla de Tukey, las observaciones anómalas serán aquellas cuyo valor sea mayor en términos absolutos a 1.5 veces el RIC, y serán representados por puntos más allá de los extremos de los bigotes. Si no existen valores anómalos los límites de los bigotes del diagrama coincidirán con los valores mínimo y máximo de la variable, aunque es este caso la longitud del bigote tiene que ser 1.5 veces el RIC.

Ejemplo 1.24. con Excel. Para detectar casos anómalos utilizando la regla de Tukey podemos:

calcular nosotros los umbrales y determinar si una observación es o no anómala.
dibujar el diagrama de caja y bigotes.

Abrimos el fichero ej_1_20.xlsx.

Una vez abierto el libro de Excel, nos situamos en la celda G1.

En primer lugar, vamos a realizar un gráfico de caja y bigotes. Hacemos clic en Insertar, luego en el botón (Insertar gráfico de estadística) y seleccionamos: Caja y bigotes. Por defecto, se abre una plantilla vacía de dibujo. Si hacemos clic en cualquier parte de esta plantilla se abrirá el menú de Diseño de gráfico, debe ser similar a la que se ilustra en la Figura 1.31.

Figura 1.31: Opciones de diseño de gráfico

Hacemos clic en Seleccionar datos, se abrirá la siguiente ventana:

Figura 1.32: Ventana de selección de datos en gráfico.

Observamos que por defecto se ha seleccionado como Rango de datos del gráfico la celda/rango en el que estamos. Seleccionamos nuestro rango de datos (A1:A16). Como en este rango se ha seleccionado la celda A1 que es un texto, su contenido pasará a ser el nombre de la serie de datos, ya no será Serie 1. También tenemos tres botones que sirven para: Agregar un nueva serie de dato; y Modificar o Quitar la serie de seleccionemos.

Por defecto siempre queda seleccionado como rango de datos del gráfico la celda o rango de celdas que hayamos seleccionado previamente a realizar la selección de gráfico. De hecho, en la mayoría de ocasiones se hace así porque se evitan pasos.

Para crear el gráfico hacemos clic en Aceptar. Nuestro gráfico tendrá la siguiente apariencia.

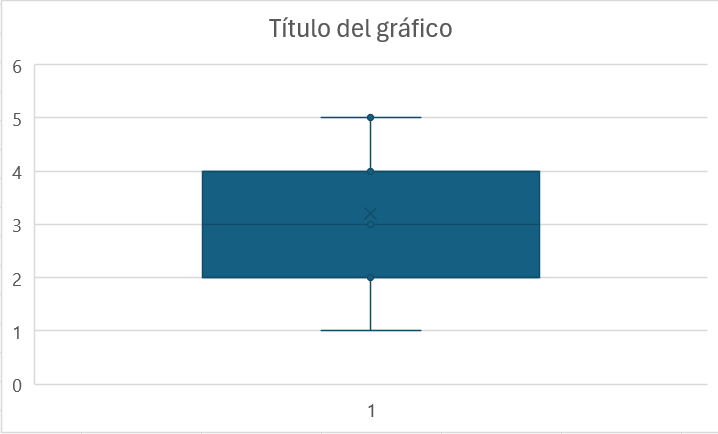
Figura 1.33: Diagrama de caja y bigotes por defecto.

Ahora es el momento de realizar algunas mejoras sobre el gráfico, entre ellas:

Eliminar las líneas horizontales de división: las seleccionamos haciendo clic sobre ellas y pulsamos la tecla Supr.
Eliminar los valores del eje vertical y del eje horizontal: hacemos clic sobre los ejes y los borramos pulsando la tecla Supr.
Agregar las etiquetas: hacemos clic sobre la caja del gráfico y pulsamos el botón derecho del ratón. Seleccionamos la opción: Agregar etiquetas de datos.
Cambiamos color de relleno y líneas: hacemos clic sobre la caja del gráfico y hacemos pulsamos el botón derecho del ratón. Seleccionamos la opción: Dar formato a la serie de datos…. Clicar sobre el primer botón, que es relleno y línea, y cambiar el color del relleno de la caja y el color de las líneas.
cambiamos el título del gráfico: hacemos doble clic sobre el título y lo cambiamos a: Diagrama de caja y bigotes de la Experiencia.

Dedicad un tiempo a mirar y probar otras opciones de relleno, borde, etc.

El resultado final debería ser similar al que se muestra en la Figura 1.34.

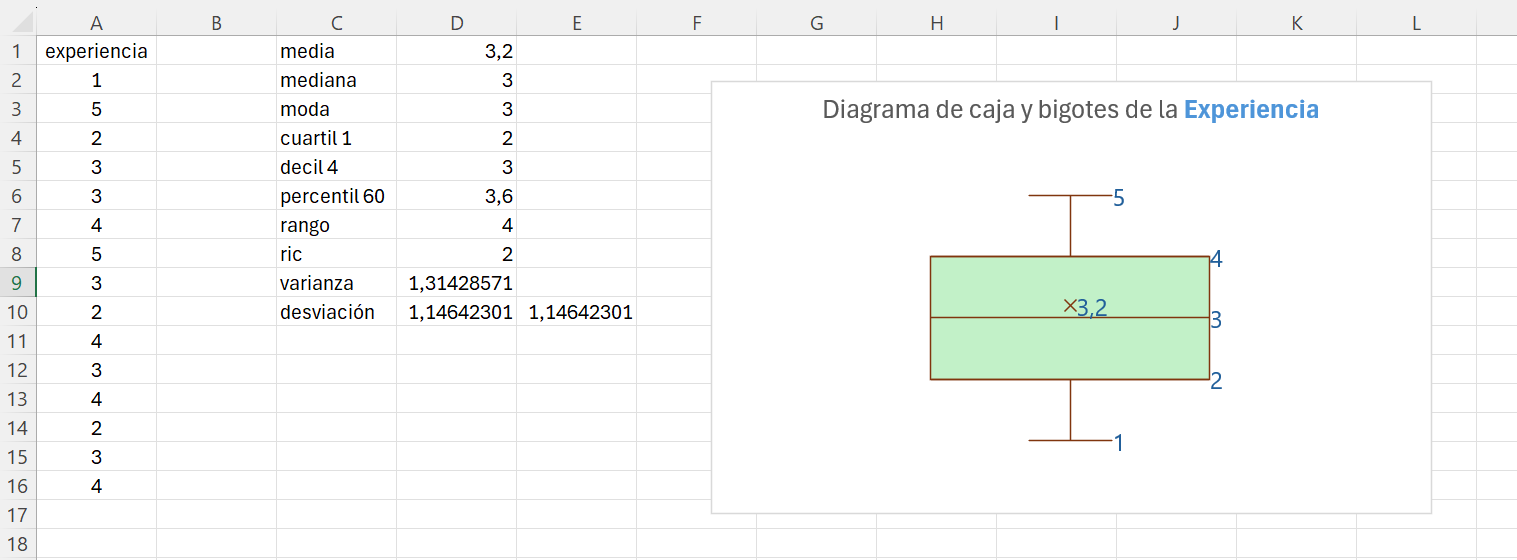
Figura 1.34: Diagrama de caja y bigotes de la experiencia.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: ej_1_24.

En la animación que tienes disponible en [https://www.uv.es/ticstat/ej_1_24_excel.gif](https://www.uv.es/ticstat/ej_1_24_excel.gif) encontrarás cómo se realizado el gráfico de caja y bigotes de la Figura 1.34.

1.9 Tasas de variación

Las tasas de variación permiten comparar una magnitud en dos periodos de tiempo. Podemos hablar de tasas de variación absoluta y tasas de variación relativas.

Si queremos analizar cómo ha variado/cambiado una magnitud en el periodo $t$ respecto al periodo anterior $(t-1)$ calculamos una tasa de variación absoluta ($TVA$). Así, tenemos que: \[TVA = X_t - X_{t-1} \tag{1.33}\]

El principal inconveniente de trabajar con tasas de variación absoluta es que dependen de las unidades de medida de la variable o magnitud con la que estamos trabajando y/o del valor de partida.

El problema anterior queda resuelto si consideramos una medida que sea adimensional, la tasa de variación relativa.

Una tasa de variación relativa ($TVR$) se obtiene al dividir la tasa de variación absoluta entre el valor de la magnitud en el periodo de referencia $(t-1)$. Así pues,\[TVR=\frac{TVA}{X_{t-1}}=\frac{ X_t - X_{t-1}}{X_{t-1}} \tag{1.34}\]

La Ecuación 1.34 está expresada en tanto por uno. Lo normal es hablar/expresar las tasas de variación relativa en tanto por ciento. Por tanto, las tasas de variación relativa suelen calcularse a partir de la siguiente expresión:\[TVR=\frac{TVA}{X_{t-1}}=\frac{ X_t - X_{t-1}}{X_{t-1}}\cdot 100\]

1.10 Resumen descriptivo con Excel

Excel cuenta con una herramienta de análisis de datos entre cuyas opciones se encuentra la función Estadística descriptiva.

Verifica que tienes activada la herramienta de análisis de datos en Excel. Si no la tienes, actívala ahora. En [https://www.uv.es/ticstat/instalar_herramienta_analisis_datos.gif](https://www.uv.es/ticstat/instalar_herramienta_analisis_datos.gif) tienes una animación que te guiará en el proceso de activación.

Vamos a ver cómo usar esta función y los resultados que proporciona utilizando los datos que venimos arrastrando a lo largo del tema; abrimos el archivo ej1-22-2.xlsx. Nuestra hoja de Excel debería ser similar a la que se muestra en la Figura 1.35

Figura 1.35: Resultado final del ejemplo 1.22. con Excel.

Seleccionamos Datos > Análisis de datos > Estadística descriptiva. Se abre el cuadro de diálogo de la función, como se reproduce en la Figura 1.36.

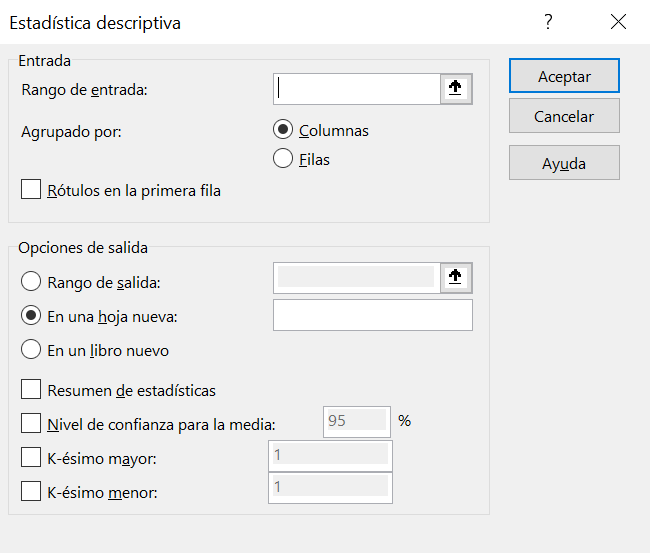
Figura 1.36: Cuadro de diálogo de la función: Estadística descriptiva.

Seleccionamos el rango donde se encuentran nuestros datos, el rango A1:A17. Como hemos seleccionado el encabezado de la columna, marcamos la opción Rótulos en la primera fila.

Como opción de salida indicamos que queremos que la función devuelva el resultado a partir de la celda G1. En ocasiones interesa que el resultado se devuelva en otra hoja del libro actual de trabajo o en un nuevo libro Excel.

Marcamos la opción Resumen de estadísticas, que nos proporcionará muchas de las medidas que hemos estudiado a lo largo de este capítulo. Entre los resultados de Resumen de estadísticas obtendremos el máximo y mínimo de la variable. Si queremos obtener, por ejemplo, los 3 mayores y menores valores, marcamos K-ésimo mayor y K-ésimo menor e insertamos el valor 3. No marcamos la opción Nivel de confianza para la media porque se refiere al cálculo de un intervalo de confianza para la media y esto se estudia en un curso de Inferencia Estadistica.

Una vez seleccionadas nuestras opciones, hacemos clic en el botón Aceptar. El resultado obtenido será el que se reproduce en la Figura 1.37.

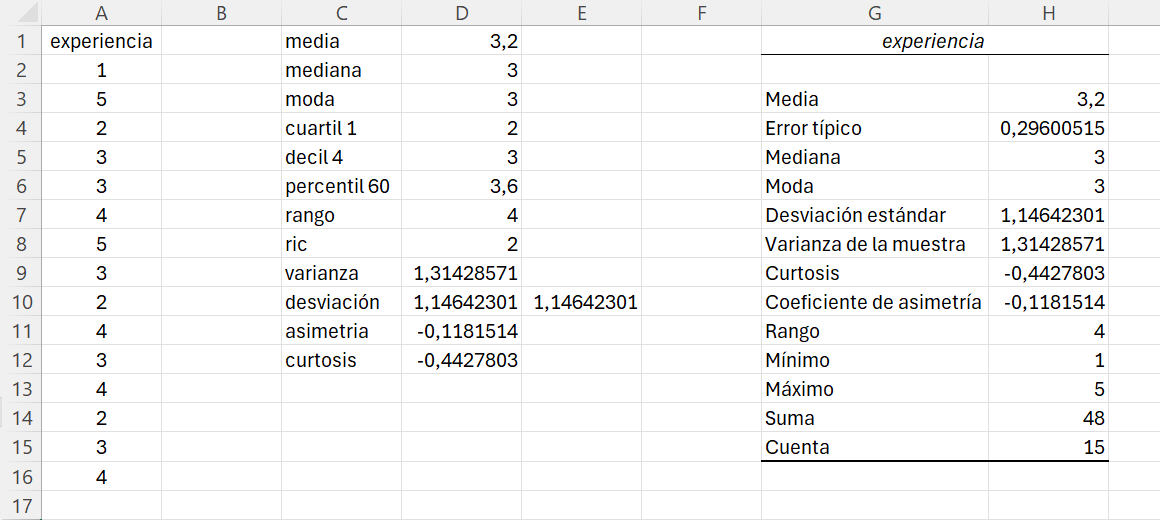
Figura 1.37: Estadística descriptiva de la experiencia.

Salvo el error típico, que se utiliza para calcular un intervalo de confianza paa la media y que es objeto de estudio en Inferencia Estadística, el resto de medidas proporcionadas por la función Estadística descriptiva son conocidas. Aclarar que cuenta hace referencia al número de observaciones y suma es el resultado de sumar todos los valores de la variable $(\sum x_i)$.

Guardad en vuestra carpeta de trabajo la hoja Excel con el nombre: estadistica-descriptiva.

Puedes seguir el proceso descrito en este apartado en la animación que encontrarás en [https://www.uv.es/ticstat/estadistica_descriptiva.gif](https://www.uv.es/ticstat/estadistica_descriptiva.gif).

1.11 Ejercicios

Ejercicio 1.1 Indica de qué tipo es cada una de las siguientes variables:

Tasa de absentismo
Nivel de estudios (sin estudios, primaria, secundaria, FP superior, universitario)
Renta disponible (en €)
Horas de formación en prevención
Características de las relaciones de trabajo (muy buenas, buenas, regulares, malas, muy malas)
¿Experiencia laboral previa? (sí o no)

Ejercicio 1.2 Una empresa está interesada en contratar un técnico en prevención de riesgos laborales (PRL). Para evaluar el nivel de los candidatos, el responsable de RRHH de una empresa multinacional elabora un test de 50 preguntas. En un estudio piloto, somete este test a una muestra de 10 técnicos de PRL. El número de respuestas acertadas por los individuos de la muestra fueron.

42 29 21 37 40 33 38 26 39 47

Calcula la media del número de respuestas acertadas.

Ejercicio 1.3 Para una muestra de 24 técnicos en PRL se observaron los siguientes porcentajes de compensación total por pago de bonus.

Compensación	Técncios PRL
7	10
10	7
13	5
15	2

Calcula la varianza de la compensación total por pago de bonus.

Ejercicio 1.4 Atendiendo a los resultados que has obtenido en el Ejercicio 1.3, ¿puede considerarse representativa del conjunto de técnicos en PRL analizados la media de compensación que has calculado? Justifica tu respuesta con el cálculo de la oportuna medida estadística.

Ejercicio 1.5 A partir de los datos del Ejercicio 1.3, ¿qué compensación total es superada por aproximadamente el 25% de los técnicos en PRL? Calcula la medida estadística mostrando el proceso de cálculo.

Ejercicio 1.6 A partir de los datos del Ejercicio 1.3, calcula la mediana de la compensación total por pago de bonus.

Ejercicio 1.7 Transcurrido el tiempo, el test diseñado por el responsable de RRHH del Ejercicio 1.2 se ha venido utilizando en los procesos de selección de todas las empresas del grupo multinacional. Ahora se encuentra analizando los resultados de los test en dos de estas empresas, que ha resumido en la siguiente tabla:

Medida	Empresa Pavoro S.A	Empresa Segura S.A
Mediaderespuestaacertadas	42.66	36.06
Desviación típica de respuestas acertadas	4.68	7.88

El último candidato que realizó el test en la empresa A obtuvo 45 respuestas correctas, mientras que el último candidato que lo hizo en la empresa B respondió correctamente a 40. El responsable de RRHH se pregunta, ¿qué candidato ha obtenido, en términos relativos, un mayor número de respuestas correctas?

Ejercicio 1.8 En base a la información del Ejercicio 1.7, el responsable de RRHJ se pregunta, ¿en qué empresa existe una mayor dispersión relativa en las respuestas contestadas correctamente al test? Responde a su pregunta calculando la oportuna medida estadística.

Ejercicio 1.9 De acuerdo con las estadísticas de absentismo de FREMAP, la tasa de absentismo en 2019 se situó en el 5.9%, en tanto que en 2022 fue del 6.7%. Calcula, para el período 2019-2022, la variación relativa de la tasa de absentismo e interpreta el resultado obtenido.

Ejercicio 1.10 Utilizanzo Excel, calcular el salario bruto medio anual de los trabajadores españoles a los que hace referencia el Ejemplo 1.10. (Pista: Tomar como referencia el ejemplo 1.11. con Excel.)

Ejercicio 1.11 Calcular el rango de la variable empleados utilizando la tabla de frecuencias obtenida en el ejemplo 1.8 con Excel.

Ejercicio 1.12 Con los datos del Ejemplo 1.9, utiliza la función SUMAPRODUCTO() en el cálculo de la varianza.

Ejercicio 1.13 Abre el fichero ej_1_22-2.xlsx y calcula los valores tipificados. ¿Hay alguna observación anómala?

\(x_i\)	\(n_i\)
\(x_i\)	\(n_i\)
\(x_1\)	\(n_1\)
\(x_2\)	\(n_2\)
\(\vdots\)	\(\vdots\)
\(x_i\)	\(n_i\)
\(\vdots\)	\(\vdots\)
\(x_I\)	\(n_I\)

\(x_i\)	\(f_i\)
\(x_1\)	\(f_1\)
\(x_2\)	\(f_2\)
\(\vdots\)	\(\vdots\)
\(x_i\)	\(f_i\)
\(\vdots\)	\(\vdots\)
\(x_I\)	\(f_I\)

\(x_i\)	\(n_i\)	\(N_i\)	\(f_i\)	\(F_i\)
\(x_1\)	\(n_1\)	\(N_1\)	\(f_1\)	\(F_1\)
\(x_2\)	\(n_2\)	\(N_2\)	\(f_2\)	\(F_2\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(x_i\)	\(n_i\)	\(N_i\)	\(f_i\)	\(F_i\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(x_I\)	\(n_I\)	n	\(f_I\)	1
	———		———
	\(\sum=n\)		\(\sum=1\)

\(L_{i-1},L_i\)	\(n_i\)	\(N_i\)	\(f_i\)	\(F_i\)
\([L_0,L_1[\)	\(n_1\)	\(N_1\)	\(f_1\)	\(F_1\)
\([L_1,L_2[\)	\(n_2\)	\(N_2\)	\(f_2\)	\(F_2\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\([L_{i-1},L_i[\)	\(n_i\)	\(N_i\)	\(f_i\)	\(F_i\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\([L_{I-1},L_I]\)	\(n_I\)	n	\(f_I\)	1
	———	——
	\(\sum=n\)	\(\sum=1\)

\(x_i\)	\(n_i\)	\(x_i \cdot n_i\)
\(x_1\) 1	1 \(n_1\)	1 \(x_1\cdot n_1\)
\(x_2\) 2	3 \(n_2\)	6 \(x_2\cdot n_2\)
\(x_3\) 3	5 \(n_3\)	15 \(x_3\cdot n_3\)
\(x_4\) 4	4 \(n_4\)	16 \(x_4\cdot n_4\)
\(x_5\) 5	2 \(n_5\)	10 \(x_5\cdot n_5\)
	———	————
	\(n=15\)	\(\sum=48\)

A (\(k=1\))	\(\rightarrow\)	\(N_A=150\)	\(\bar{S}_A=1,400\)
B (\(k=2\))	\(\rightarrow\)	\(N_B=125\)	\(\bar{S}_B=1,450\)
C (\(k=3\))	\(\rightarrow\)	\(N_C=200\)	\(\bar{S}_C=1,525\)

Salarios	Trabajadores
\([1,000-1,500[\)	150
\([1,500-2,000[\)	200
\([2,000-2,500[\)	300
\([2,500-3,000[\)	250
\([3,000-3,500[\)	75
\([3,500-4,000]\)	25