3 Regresión lineal simple.
3.1 Introducción
El objetivo de la teoría de la correlación es determinar la presencia y fortaleza de la relación lineal entre dos variables. La teoría de la regresión pretende explicar el comportamiento de una variable (dependiente, endógena, regresada, explicada, etc.) a partir del comportamiento de otra variable (independiente, exógena, regresando, explicativa, etc.).
La regresión pretende estimar la forma o estructura de la relación entre las dos variables objeto de estudio; esto es, el objetivo es estimar el modelo de dependencia entre las variables para posteriormente utilizarlo para generar pronósticos (predicciones) de la variable dependiente (variable Y) a partir de valores de la variable independiente (variable X).
Si pretendemos modelizar la relación de dependencia de una variable independiente \(X\) sobre la variable dependiente \(Y\), hablamos de modelo de regresión simple.
Si estudiamos cómo dos o más variables independientes \(Xs\) influyen sobre una variable dependiente \(Y\), hablamos de un modelo de regresión múltiple. La regresión múltiple se estudia en un curso más avanzado de estadística.
Las variables independientes y dependiente reciben distintos nombres.
Variable dependiente, o también: regresando, endógena, respuesta.
Variable/s independiente/s, o también: regresora/s, exógena/s, predictora/es.
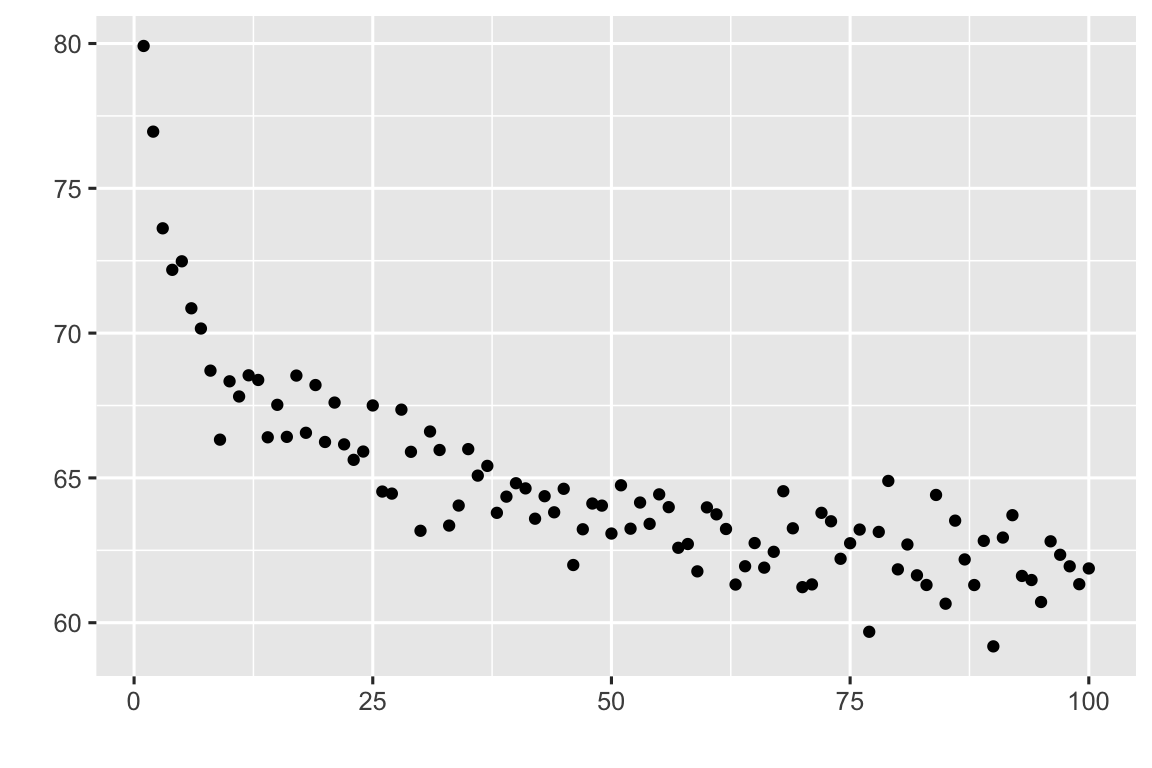
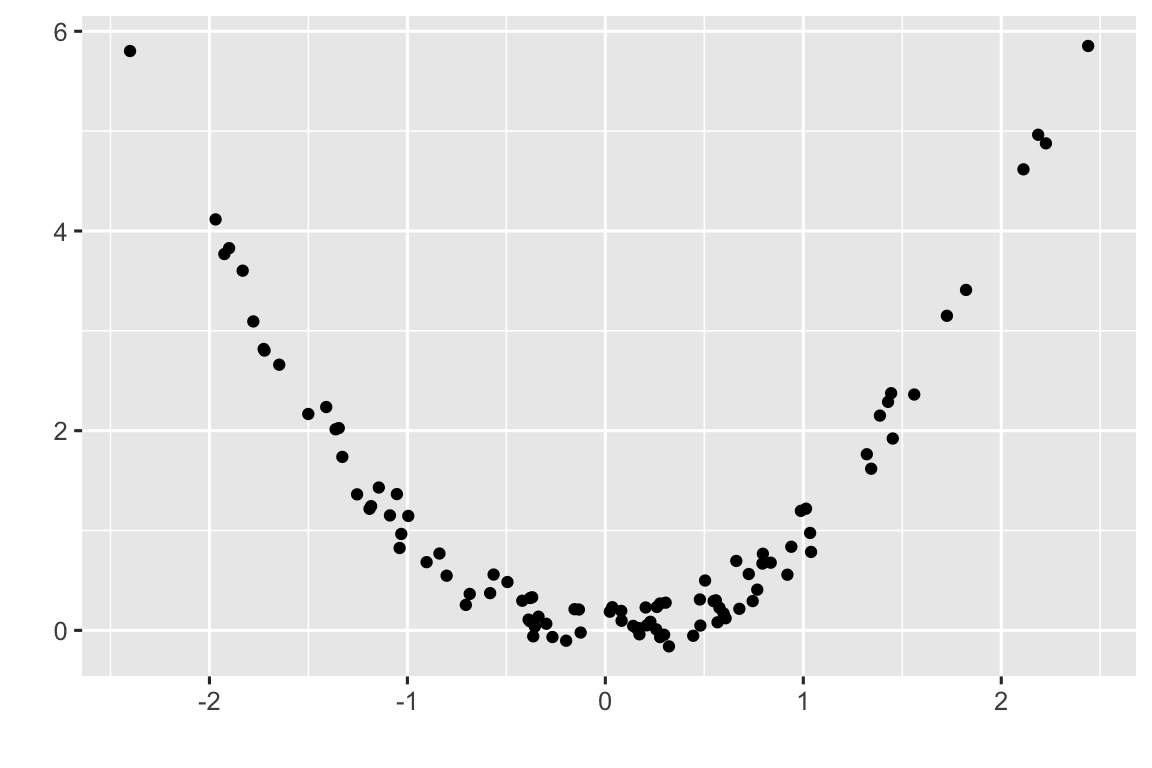
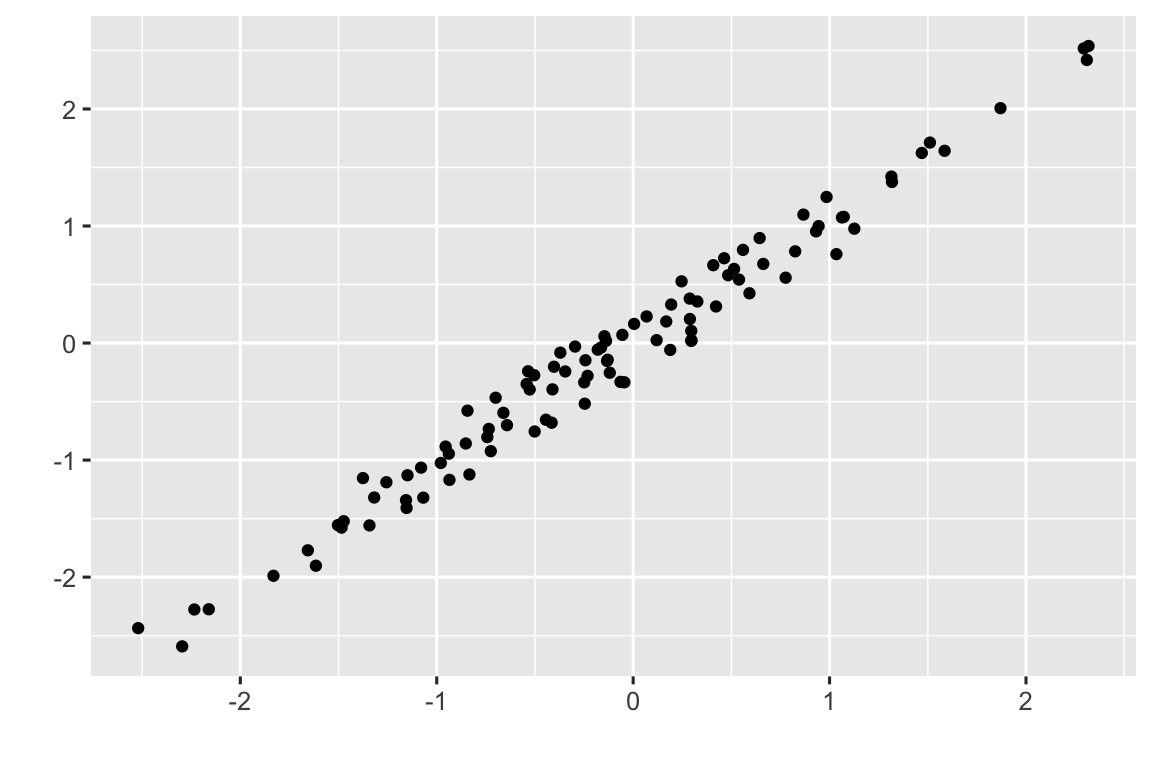
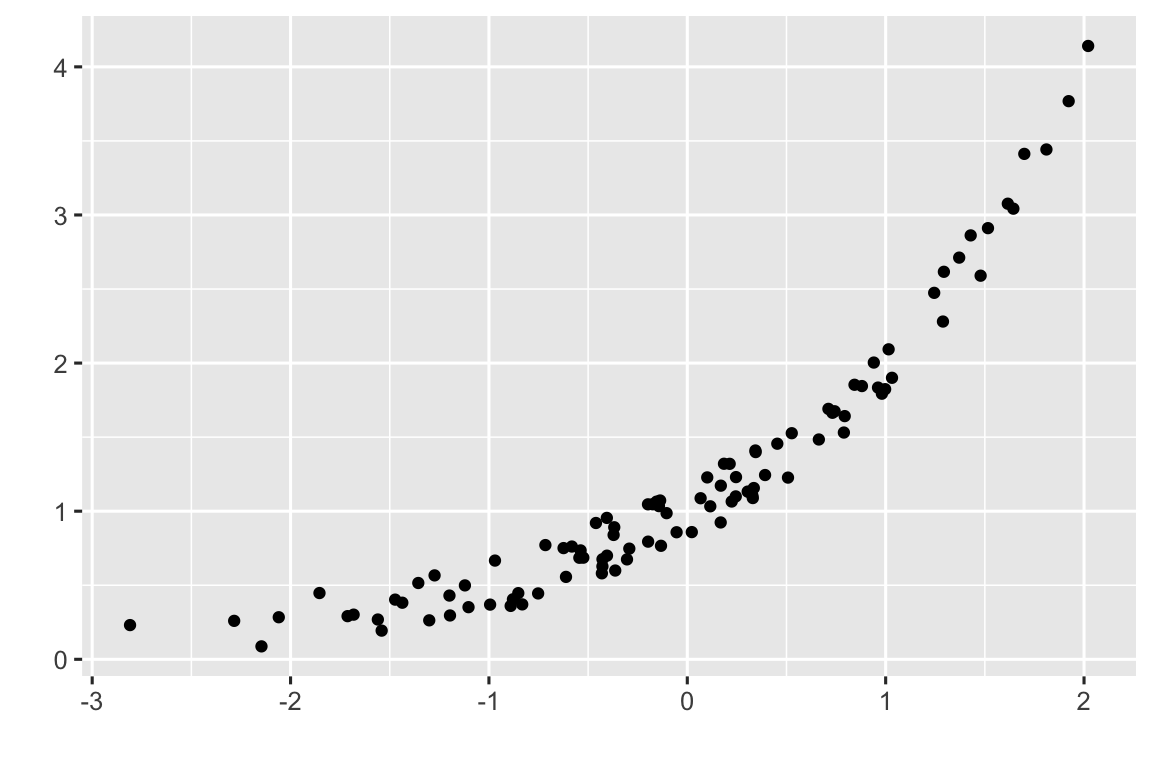
Como se ilustra en la Figura 3.1, la relación funcional entre las variables puede ser de distinto tipo: lineal, parabólica, logarítmica, exponencial, etc.
En este capítulo nos centramos en el estudio de la regresión lineal simple. En un curso más avanzado estudiaremos la regresión lineal múltiple y la inferencia sobre el modelo.
La teoría de la regresión lineal analiza la relación lineal entre dos variables desde el punto de vista de la dependencia de una respecto de la otra. En definitiva, la regresión permite pasar de una dependencia estadística a una dependencia funcional.
3.2 Método de mínimos cuadrados
En este apartado vamos a determinar cuál es la función que mejor ajusta a la nube de puntos. Concretamente, vamos a determinar la recta de regresión de \(Y\) sobre \(X\) \((Y=f(X))\) utilizando el método de mínimos cuadrados ordinarios (MCO).
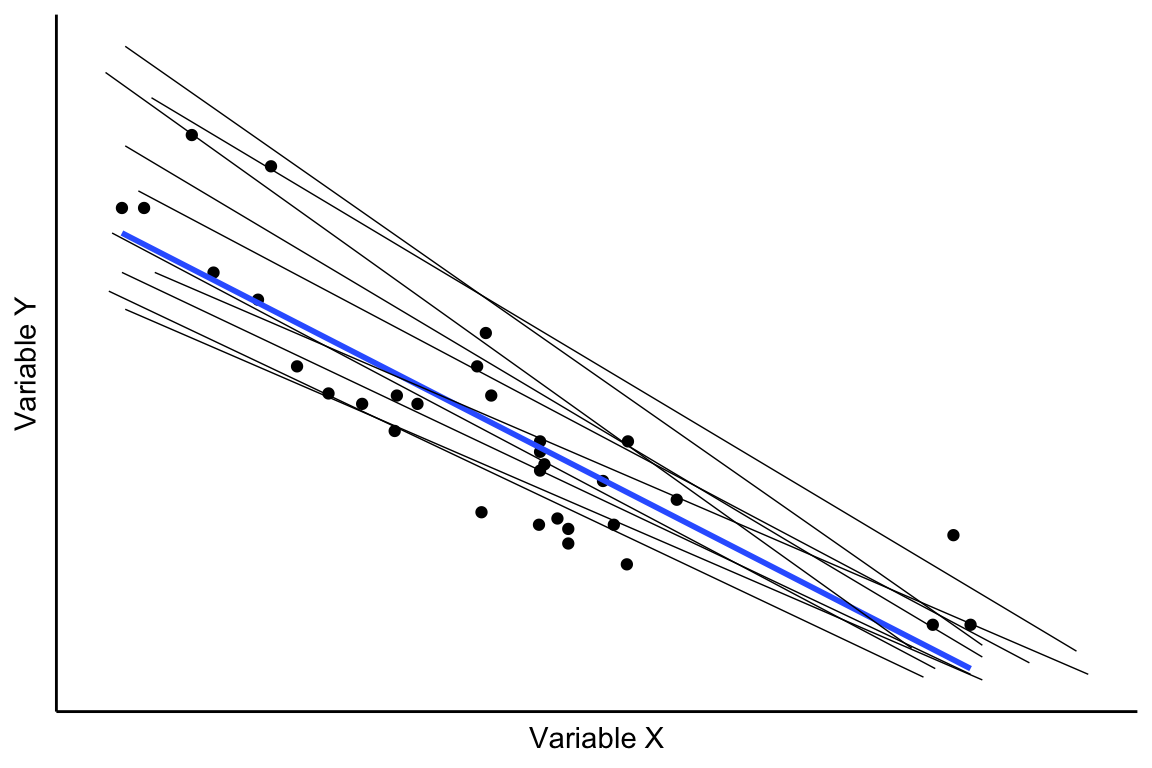
Cuando representamos un diagrama de dispersión situamos en el eje de abcisas la variable independiente (variable X) y en el eje de ordenadas la variable dependiente (variable Y). Por esa nube de puntos podemos hacer pasar infinitas rectas, como se representa en la Figura 3.2.

Consideremos una de esas rectas teóricas. En la Figura 3.3 se muestran los errores (en color rojo), que son las diferencias entre los valores observados (puntos negros en la figura) y los teóricos (puntos amarillos) obtenidos a partir del modelo estimado (recta de color azul).
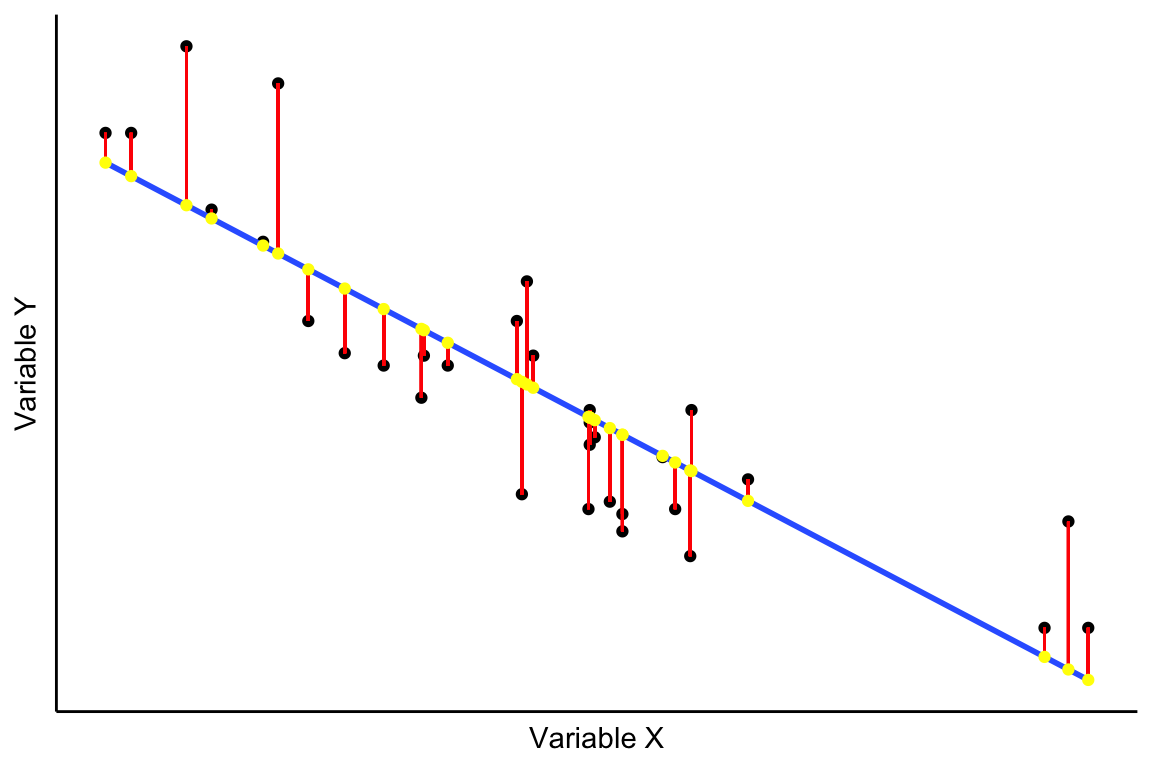
El objetivo de la técnica de mínimos cuadrados ordinarios (MCO) es elegir entre las infinitas rectas que podemos dibujar (Figura 3.2) aquella en la que los errores son mínimos (Figura 3.3), la recta de color azul en la Figura 3.2. Por tanto, el método de MCO consiste en minimizar la suma de los errores al cuadrado: \[min\displaystyle\sum_{i=1}^n e_i^2 = min \sum_{i=1}^n (y_i-y_i^*)^2= min \sum_{i=1}^n [y_i-f(x_i)]^2 \tag{3.1}\]
donde: \(y_i^*\) es el valor teórico/estimado de Y para un valor \(x_i\); \(y_i\) es el i-ésimo valor observado.
Si la curva de regresión que mejor ajusta a la nube de puntos es una recta, entonces hablamos de la regresión lineal, es decir: \[y_i^*=f(x_i)=a+b\cdot x_i \tag{3.2}\] y tendremos que minimizar la siguiente función: \[\phi=min \sum_{i=1}^n [y_i-(a+b\cdot x_i)]^2 \tag{3.3}\] Para obtener los valores de los parámetros \(a\) y \(b\) que hacen mínima la suma de cuadrados de los errores (Ecuación 3.1) se calcula la derivada parcial de \(\phi\) respecto de cada uno de los parámetros y se igualan a cero las expresiones obtenidas. El resultado de minimizar la función es: \[\begin{matrix} \displaystyle a = \overline{y} - b \cdot \overline{x}\\ \\ \displaystyle b = \frac{S_{XY}}{S^2_X} \end{matrix} \tag{3.4}\]
El parámetro \(a\) recibe el nombre de: constante, ordenada en el origen, intercepto, intersección.
El parámetro \(b\) recibe el nombre de: coeficiente de regresión.
Por tanto, la recta de regresión de Y sobre X (\(Y=f(X)\), que se lee: Y en función de X), será: \[Y^* = a + b \cdot X \tag{3.5}\] siendo: \(a = \overline{y} - b \cdot \overline{x}\quad\) y \(\quad b=\displaystyle\frac{S_{XY}}{S^2_X}\)
Ejemplo 3.1 Se desea analizar la relación entre la variable X: “Edad de la empresa (años desde su constitución hasta la fecha)” y la variable Y: “Eficiencia productiva (en puntos porcentuales)”. Para ello, se dispone de la siguiente información correspondiente a una muestra de 5 empresas:
| X:Edad | Y:Eficiencia |
|---|---|
| 5 | 50 |
| 10 | 72 |
| 12 | 70 |
| 15 | 78 |
| 18 | 95 |
Sabiendo que media de edad de las empresas es de 12 años, con una varianza 24.5 (años\(^2\)). Responde a las siguientes preguntas:
- Obtén el vector de medias y la matriz de varianzas-covarianzas.
- ¿Qué puedes decir acerca de la relación lineal entre la edad de la empresa y la eficiencia productiva? Justificar la respuesta con el cálculo de la oportuna medida estadística.
- Estima la ecuación de regresión lineal que permita explicar el comportamiento de la eficiencia en función de la edad de la empresa.
Solución:
Apartado (a): Como es dato del ejemplo que \(\overline{x}=12\) y que \(S^2_{X}=19.6\), nos centramos en calcular \(\overline{y}\), \(S^2_{Y}\) y \(S_{XY}\) utilizado las expresiones ya conocidas: \[\overline{y}=\frac{\displaystyle\sum_{i=1}^{I=5}y_i}{n}\] \[S^2_Y=\frac{\displaystyle\sum_{i=1}^{I=5}(y_i-\overline y)^2}{n-1}\] \[S_{XY}=\frac{\displaystyle\sum_{i=1}^{I=5}(x_i - \overline{x}) \cdot (y_i - \overline {y})}{n-1}\] Para calcular la medidas anteriores, ampliamos la tabla facilitada en el ejemplo para realizar los cálculos intermedios, tal y como se muestra en la tabla Tabla 3.2.
| X:Edad | Y:Eficiencia | \(x_i-\bar{x}\) | \(y_i-\bar{y}\) | \((y_i-\bar{y})^2\) | \((x_i-\bar{x})\cdot (y_i-\bar{y})\) |
|---|---|---|---|---|---|
| 5 | 50 | -7 | -23 | 529 | 161 |
| 10 | 72 | -2 | -1 | 1 | 2 |
| 12 | 70 | 0 | -3 | 9 | 0 |
| 15 | 78 | 3 | 5 | 25 | 15 |
| 18 | 95 | 6 | 22 | 484 | 132 |
| — | — | — | |||
| \(\sum=365\) | \(\sum=1,048\) | \(\sum=310\) |
Ya estamos en disposición de calcular nuestras medidas. \[\overline{y}=\frac{\displaystyle\sum_{i=1}^{I=5}y_i}{n}=\frac{365}{5}=73\hspace{1mm}\text{(puntos porentuales)}\] \[S^2_Y=\frac{\displaystyle\sum_{i=1}^{I=5}(y_i-\overline y)^2}{n-1}=\frac{1,048}{5-1}=262\hspace{1mm}\text{(puntos porcentuales}^2)\] \[S_{XY}=\frac{\displaystyle\sum_{i=1}^{I=5}(x_i - \overline{x}) \cdot (y_i - \overline {y})}{n-1}=\frac{310}{5-1}=77.5\hspace{1mm}\text{(años} \cdot \text{puntos porcentuales)}\] y de resumir la información en el vector de medias y en la matriz de varianzas-covarianzas. \[m=\begin{pmatrix} \overline{x}\\ \overline{y} \end{pmatrix}=\begin{pmatrix} 12\\ 73 \end{pmatrix} \hspace{15mm} V=\begin{pmatrix} {S^2_X} & S_{XY} \\ & S^2_Y \end{pmatrix}=\begin{pmatrix} 24.5 & 77.5 \\ & 262 \end{pmatrix}\] Apartado (b): Basándonos en el resultado de la covarianza, podemos decir que hay una relación lineal positiva entre Edad y Eficiencia de las empresas. Por término medio, cuanto mayor es la edad de las empresas (variable \(X\)) mayor es también la eficiencia productiva (variable \(Y\)). Sin embargo, la covarianza únicamente nos informa del sentido de la asociación entre las variables porque, recordemos, no es una medida adimensional, depende de las unidades de medida de las variables. Por tanto, para analizar cómo es la intensidad de dicha relación lineal calculamos el coeficiente de correlación de Pearson, que sí es una medida adimensional. \[r_{XY}=\frac{S_{XY}}{S_X \cdot S_Y}=\frac{77.5}{\sqrt{24.5}\cdot \sqrt{262}}\approx 0.9673\] por lo que podemos concluir que la relación lineal positiva observada es muy fuerte, el coeficiente de correlación se acerca a 1.
¿Es significativo el valor obtenido de la correlación? \[r_{XY}=0.9673>\frac{2}{\sqrt{5}}=0.8944\] En consecuencia, la correlación entre Edad y Experiencia es significativa.
Apartado (c): Queremos obtener la estructura funcional: \(Eficiencia=f(Edad)\), suponiendo una relación lineal, es decir: \[Eficiencia^*= a + b \cdot Edad\hspace{2mm}\rightarrow\hspace{2mm} Y^*= a + b\cdot X\] A partir de la Ecuación 3.4, calculamos los valores de los parámetros: \(a\) y \(b\). Calculamos primero \(b\) porque su valor lo necesitamos para calcular \(a\). \[b = \frac{S_{XY}}{S^2_X}= \frac{77.5}{24.5}\approx 3.1633\] \[a = \overline{y} - b \cdot \overline{x} = 73 - 3.1633 \cdot 12 \approx 35.0404\] Por tanto, nuestro modelo estimado/teórico es: \[Y^*=35.0404 + 3.1633\cdot X\] es decir, \[Eficiencia^*=35.0404 + 3.1633\cdot Edad\] Para cada observación (\(x_i,y_i\)), los valores teóricos de la eficiencia (\(y^*_i\)) se obtendrán al sustituir el valor de \(x_i\) (edad de la empresa) en la expresión anterior, es decir: \[y^*_i=35.0404 + 3.1633\cdot x_i\]
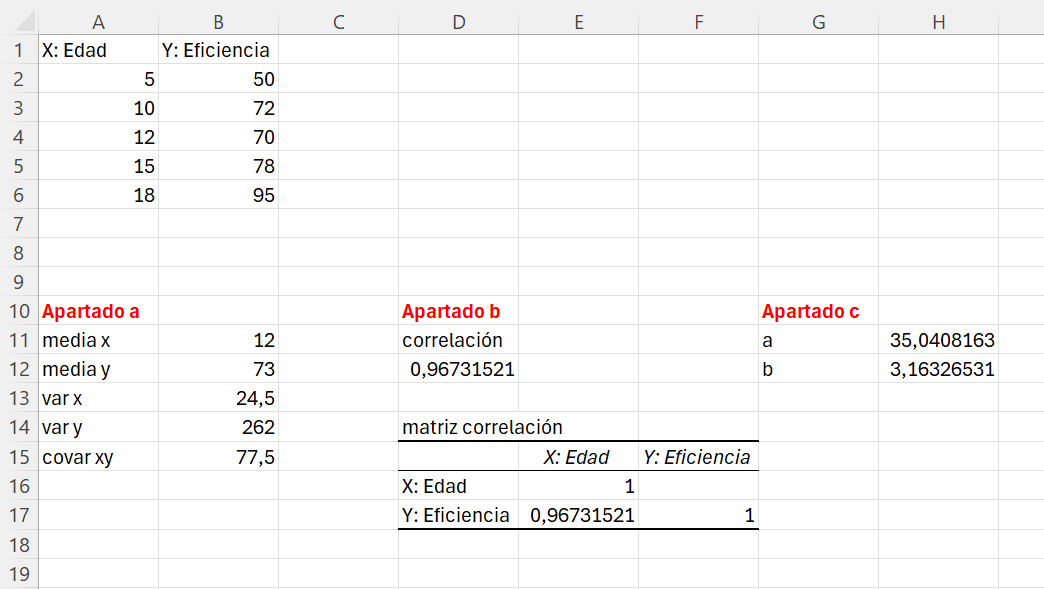
Ejemplo 3.1. con Excel: Reproducimos los datos del Ejemplo 3.1 en un libro nuevo de Excel.
Escribimos los siguientes textos en las correspondientes celdas:
- A10: Apartado a
- E10: Apartado b
- D10: Apartado c
- A11: media x
- A12: media y
- A13: var x
- A14: var y
- A15: covar xy
- D11: correlacion
- D14: matriz correlacion
- G11: a
- G12: b
En este punto, ya sabemos cómo calcular todas las medidas de interés utilizando las funciones de Excel, con la excepción de los parámetros a y b de la regresión.
Para calcular la ordenada en el origen, parámetro a, utilizamos la función INTERSECCION.EJE(); y para estimar el coeficiente de regresión, parámetro b, la función PENDIENTE(). Ambas funciones tienen los mismos argumentos. En el argumento conocido_y tenemos que seleccionar el rango de datos de la variable dependiente (variable Y: Eficiencia), y en conocido_x el de la variable independiente (variable X:Edad).
Resolvemos las cuestiones del ejemplo intoduciendo las siguientes fórmulas en sus respectivas celdas:
- B11: =promedio(A2:A6)
- B12: =promedio(B2:B6)
- B13: =var.s(A2:A6)
- B14: =var.s(B2:B6)
- B15: =covarianza.m(A2:A6;B2:B6)
- D12: =coef.de.correl(A2:A6;B2:B6)
- H11: interseccion.eje(B2:B6;A2:A6)
- H12: pendiente(B2:B6;A2:A6)
Verifica que tienes activada la herramienta de análisis de datos en Excel. Si no la tienes, actívala ahora. En [https://www.uv.es/ticstat/instalar_herramienta_analisis_datos.gif](https://www.uv.es/ticstat/instalar_herramienta_analisis_datos.gif) tienes una animación que te guiará en el proceso de activación.
En la celda D15 vamos a obtener la matriz de correlación; para ello, realizamos la selección Datos > Análisis de datos > Coeficiente de correlación. En el cuadro de diálogo seleccionamos el rango donde se encuentran nuestros datos. Si seleccionamos los encabezados tenemos que marcar la opción Rótulos en la primera línea. Establecemos como rango de salida la celda D15 y clicamos en Aceptar. En la celda D15 tendremos la matriz de correlación.
Como ya sabemos, la opción Covarianza de la herramienta de análisis de datos de Excel proporciona la matriz de varianzas-covarianzas de la población, no de la muestra. Además, la opción Coeficiente de correlación produce la matriz de correlación, que es la misma tanto si trabajamos con una muestra como si lo hacemos con la población.
El resultado final debería ser similar al que se muestra en el Figura 3.4.
Guardad el fichero de trabajo con el nombre ej_3_1.
Puedes seguir los pasos de resolución del ejemplo en la animación que se encuentra en [https://www.uv.es/ticstat/ej3_1.gif](https://www.uv.es/ticstat/ej3_1.gif)
Si sustituimos \(a\) y \(b\) (Ecuación 3.4) por sus respectivos valores en la Ecuación 3.5, obtenemos la siguiente expresión equivalente de la regresión lineal: \[\begin{matrix} Y^*=a+b\cdot X=\left(\overline{y}-\displaystyle{\frac{S_{XY} \cdot \overline{x}}{S^2_X}}\right) + \displaystyle{\frac{S_{XY}}{S^2_X}} \cdot X \\ \\ Y^*=\overline{y}+\displaystyle{\frac{S_{XY}}{S^2_X}}\cdot (X-\overline{x})\\ \end{matrix} \tag{3.6}\]
Ejemplo 3.2 El Instituto Valenciano para el Estudio de la Empresa Familiar (IVEFA) ha publicado recientemente un informe que contiene datos de una muestra de 350 empresas valencianas. Esta información permite analizar, por ejemplo, la relación entre el número de trabajadores (variable \(X\)) y la facturación anual en cientos de miles de euros (variable \(Y\)) de las empresas valencianas. Los resultados se muestran resumidos a continuación: \[m=\begin{pmatrix} \overline{x}=14 \\ \overline{y}=100 \end{pmatrix} \qquad V=\begin{pmatrix} S^2_X=2^2 & S_{XY}=45 \\ & S^2_Y=25^2 \end{pmatrix}\] A partir de los datos anteriores:
¿Qué puedes decir acerca de la existencia o no de relación entre las variables estudiadas? Interpreta, en el contexto del problema, tanto (1) el sentido, como (2) la fortaleza de esta posible relación.
Estima el modelo de regresión que permita analizar el efecto de la facturación anual de las empresas valencianas sobre el número de trabajadores.
Solución
Apartado (a): Para analizar el sentido de la posible asociación o relación lineal entre las variables consideradas nos fijamos en la covarianza. Como la covarianza es positiva (\(S_{XY}=45\)) podemos decir que la relación lineal es positiva, esto es, valores altos de número de empleados se asocian con valores altos de facturación y valores bajos de número de empleados se asocian con valores bajos de facturación, como podemos observar en la Figura 2.12.
Expresado de otra forma, en media, cuanto mayor es el número de trabajadores, mayor es la facturación de la empresa o al contrario. En cualquier caso, si la covarianza es positiva las variables varían conjuntamente en el mismo sentido.
En cuanto a cómo de fuerte es esa relación, tenemos que calcular el coeficiente de correlación lineal de Pearson: \[r_{XY}=\frac{S_{XY}}{S_X \cdot S_Y}=\frac{45}{2 \cdot 25}=0.9\] En base al resultado obtenido podemos decir que la relación lineal entre número de trabajadores y facturación de la empresa es muy fuerte. ¿Es significativa la correlación?
Apartado (b): Haciendo uso de la Ecuación 3.6 y sustituyendo por los correspondientes valores, se tiene: \[Y^*=\overline{y}+\frac{S_{XY}}{S^2_X}\cdot (X-\overline{x}) = 100+\frac{45}{2^2}\cdot (X-14)\] La recta de regresión estimada de la facturación en función del número de trabajadores es: \[Y^*=-57.5 + 11.25\cdot X\]
3.3 Interpretación de los coeficientes del modelo
El parámetro \(a\) es la ordenada en el origen, es decir, es el punto de corte en el eje de ordenadas, será el punto \((x=0,y^*=a)\). Por tanto, la interpretación literal del parámetro \(a\) es: si \(x\) toma el valor 0, entonces se espera que \(y\) tome el valor \(a\).
El parámetro \(b\) es el coeficiente de regresión (de Y sobre X) e indica que si X se incrementa en 1 unidad (en las unidades de medida de X) se estima que Y se incremente (o decrezca) en \(b\) unidades (en las unidades de medida de Y). De hecho, como puede verse en la Figura 3.5, \(b\) es la pendiente de la recta de regresión.
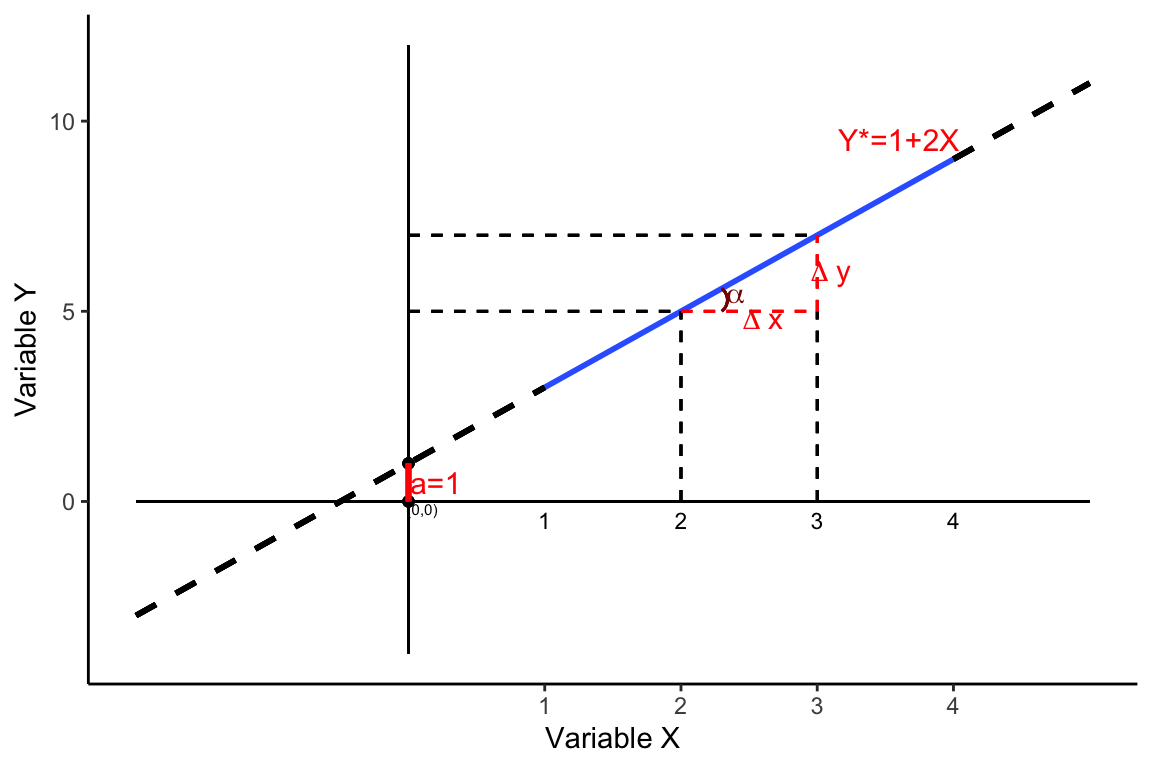
Como vemos en la Figura 3.5, la variable X toma valores entre 1 y 4 (rango de valores de X). La recta que mejor ajusta a la nube de puntos (en color azul) se estima para el conjunto de datos \((x_i,y_i)\) observado; es decir, la relación solo es válida dentro de ese rango de valores de X. En la Figura 3.5 se ha prolongado la recta de regresión (línea negra discontinua), tanto por debajo del valor 1 de X como por encima del valor 4. No obstante, suponer que la relación entre las variables es lineal fuera de este rango puede ser (muy) aventurado en muchas situaciones. El punto donde la recta prolongada corta el eje de ordenadas es el parámetro \(a\), la constante u ordenada en el origen de la regresión. El parámetro \(b\) es la pendiente de la recta de regresión: \[b=tg\alpha=\frac{\Delta y}{\Delta x} \tag{3.7}\] Por tanto, \(b\) mide la variación de Y ante un incremento unitario de X.
- El parámetro \(a\) no suele interpretarse en la mayor parte de las aplicaciones. El motivo es que si el valor \(x=0\) no se encuentra en el rango de valores de la variable \(X\), entonces \(a\) carece generalmente de sentido. En estos casos, \(a\) se interpreta como el efecto resultante de todos aquellos otros factores que no han sido considerados en el análisis.
- El parámetro \(b\) siempre se interpreta, mide el efecto de X sobre Y.
Ejemplo 3.3 Interpreta la recta de regresión estimada en el Ejemplo 3.1.
Solución: La recta estimada en el Ejemplo 3.1 es: \[Eficiencia^*=35.0404 + 3.1633\cdot Edad\] La edad de la empresa (variable \(X\)) toma valores en el rango \(5-18\), no hay ninguna empresa con una edad de 0 años. Por tanto, si decimos que para una empresa de reciente creación (\(x_i=0\)) se esperaría una eficiencia productiva de 35.04 puntos porcentuales es porque estamos asumiendo que la relación entre edad y eficiencia sigue siendo lineal fuera del rango \(5-18\); lo cual, insisto, es muy arriesgado suponer en la mayoría de las aplicaciones prácticas.
El coeficiente de regresión \(b\) toma el valor 3.1633. Este resultado debe interpretase como sigue: por cada año adicional en la edad de la empresa se espera que la eficiencia productiva se incremente (\(b\) es positivo) en 3.1633 puntos porcentuales. Parece lógico pensar que cuanto mayor sea la experiencia de la empresa mas eficiente resulte.
Ejemplo 3.4 Interpreta, en el contexto del problema, el valor de los coeficientes de la recta de regresión obtenida en el Ejemplo 3.2.
Solución: La recta estimada en el Ejemplo 3.2 es: \[Y^*=-57.5 + 11.25\cdot X\] donde la variable \(X\) representa el número de trabajadores de la empresa, y la variable \(Y\) la facturación anual (en cientos de miles de euros).
Literalmente, el parámetro \(a\) significa que en una empresa sin trabajadores (\(x_i=0\)) la facturación anual esperada sería de -57.5 (cientos de miles de euros). En este caso es evidente que extrapolar el resultado fuera del posible rango de valores de la variable \(X\) (número de trabajadores de la empresa), -que no conocemos- no tiene sentido.
En cuanto al coeficiente de regresión (\(b\)), en media, un incremento de un empleado en la plantilla de la empresa incrementa la facturación anual de la empresa en 11.25 (cientos de miles de euros).
A la hora de interpretar los parámetros estimados \(a\) y \(b\), utilizamos términos como: se espera, se esperaría, en media, en promedio, por término medio, etc.; no se realizan afirmaciones.
3.4 Propiedades de la regresión
Al aplicar el método de mínimos cuadrados para estimar el modelo de regresión lineal se obtienen las siguientes propiedades algebraicas:
Propiedad 1. La media de los valores teóricos es igual a la media de los valores observados de Y. \[\overline{y}^*=\overline{y} \tag{3.8}\]
Propiedad 2. La suma de los errores (o residuos) es cero; por tanto, su media es cero: \[\overline{e}=0 \tag{3.9}\]
Propiedad 3. La recta de regresión minimo-cuadrática pasa por el punto \((\overline{x},\overline{y})\), que es el centro de gravedad.
Propiedad 4. La suma de los productos cruzados entre los residuos y la variable explicativa es igual a 0: \[\displaystyle \sum_{i=1}^n e_i \cdot x_i = 0 \tag{3.10}\] Vamos a comprobarlo. Para ello, sabemos que \(y_i = y_i^* + e_i\), con lo que tenemos: \[e_i= y_i - y_i^*= y_i - (a - b\cdot x_i)\] Es decir: \[\displaystyle\sum_{i=1}^n e_i \cdot x_i = \sum_{i=1}^n [y_i - (a - b\cdot X_i)] \cdot x_i = 0\]
De acuerdo con la segunda ecuación del sistema de ecuaciones normales de la regresión: \[\displaystyle -2 \cdot \sum_{i=1}^n (y_i - a - b\cdot x_i)\cdot x_i = 0\]
- Propiedad 5. La suma de los productos cruzados entre los errores y los valores ajustados o teóricos es igual a 0: \[\displaystyle\sum_{i=1}^n e_i \cdot y_i^* = 0 \tag{3.11}\] En este caso: \[\displaystyle\sum_{i=1}^n e_i \cdot (a + b \cdot x_i) = a \cdot \sum_{i=1}^n e_i + b \cdot \sum_{i=1}^n e_i \cdot x_i= 0\] puesto que \(\overline{e}=0\) y \(\displaystyle\sum_{i=1}^n e_i \cdot x_i= 0\)
Ejemplo 3.5 Comprobamos las propiedades 1 y 2 de la regresión a partir de los datos considerados en el Ejemplo 3.1 y el modelo estimado: \[Y^*=35.0404 + 3.1633\cdot X\]
Solución: A partir del modelo estimado, vamos a calcular los valores teóricos y los errores para calcular las medias de estas variables y comprobar las propiedades dadas por la Ecuación 3.8 y la Ecuación 3.9. Estos cálculos los incluimos como nuevas columnas en la tabla de datos original, como se muestra en la tabla Tabla 3.3.
| X:Edad | Y:Eficiencia | \(y^*_i\) | \(e_i=y_i-y^*_i\) |
|---|---|---|---|
| 5 | 50 | 50.8569 | -0.8569 |
| 10 | 72 | 66.6734 | 5.3266 |
| 12 | 70 | 73 | -3 |
| 15 | 78 | 82.4899 | -4.4899 |
| 18 | 95 | 91.9798 | 3.0202 |
| \(\sum=60\) | \(\sum=365\) | \(\sum=365\) | \(\sum=0\) |
Una vez obtenidos los valores teóricos calculamos su correspondiente media: \[\overline{y}=\frac{\displaystyle\sum_{i=1}^{I=5}y_i}{n}=\frac{365}{5}=73\] \[\overline{y}^*=\frac{\displaystyle\sum_{i=1}^{I=5}y^*_i}{n}=\frac{365}{5}=73\] Con lo que queda comprobado que la media de los valores teóricos es igual a la de los observados de la variable Y (variable dependiente): \[\overline{y}^*=\overline{y}\] Por otro lado, como podemos comprobar en la Tabla 3.3, siempre se cumple que la suma de los errores es cero: \[\displaystyle\sum_{i=1}^{I=5}e_i=0\] En consecuencia, la media de los errores siempre es cero: \[\overline{e}=0\]
3.5 Relación entre varianzas de la regresión
Cuando llevamos a cabo un análisis de regresión partimos de los valores observados/conocidos (\(x_i,y_i\)) y creamos dos nuevas variables: los valores teóricos o estimados (\(y^*_i\)) y los errores (\(e_i\)). Como son variables, podemos calcular las medias y las varianzas de estas variables. En este apartado se aborda la relación entre las varianzas de las variables de la regresión.
Partimos de la siguiente relación ya conocida: \[Y = Y^* + E \tag{3.12}\] donde: \(Y\) es la variable dependiente, \(Y^*\) es la variable teórica y \(E\) es el error.
Así, para los distintos valores tenemos que (ver Figura 3.3): \[y_i = y_i^* + e_i \tag{3.13}\] si restamos en ambos miembros \(\overline{y}\) y recordamos que \(\overline{y}^* =\overline{y}\), entonces: \[y_i - \overline{y} = y_i^* - \overline{y}^* + e_i\] Ahora, elevando al cuadrado ambos miembros de la expresión anterior, resolviendo el cuadrado del miembro de la derecha y sumando para todo i: \[\displaystyle\sum_{i=1}^n(y_i - \overline{y})^2 =\sum_{i=1}^n(y_i^* - \overline{y}^*)^2 + 2\sum_{i=1}^n e_i \cdot (y_i^* - \overline{y}^*) + \sum_{i=1}^n e_i^2\] Es decir: \[\displaystyle\sum_{i=1}^n(y_i - \overline{y})^2 =\sum_{i=1}^n(y_i^* - \overline{y}^*)^2 + \sum_{i=1}^n e_i^2 \tag{3.14}\]
Aplicando las propiedades de la regresión minimo-cuadrática: \[\sum_{i=1}^n e_i \cdot (y_i^* - \overline{y}^*)=\sum_{i=1}^n e_i \cdot y_i^* - \sum_{i=1}^n e_i \cdot \overline{y}^*=0\] porque la suma de los productos cruzados de los errores y los valores teóricos es cero, y la media de los errores es cero.
La expresión dada por la Ecuación 3.14 se lee de la siguiente forma:
La suma de los cuadrados totales (SCT) es igual a la suma de los cuadrados explicados por la regresión (SCR) más la suma de los cuadrados de los errores/residuos (SCE), es decir, \[SCT = SCR + SCE \tag{3.15}\]
Alternativamente, si dividimos la Ecuación 3.14 por \(n-1\): \[\frac{SCT}{n-1} = \frac{SCR}{n-1} + \frac{SCE}{n-1}\] \[\frac{\displaystyle\sum_{i=1}^n(y_i - \overline{y})^2}{n-1} = \frac{\displaystyle\sum_{i=1}^n(y_i^* - \overline{y}^*)^2}{n-1} + \frac{\displaystyle\sum_{i=1}^n e_i^2}{n-1} \tag{3.16}\] \[S^2_{Y}=S^2_{Y^*}+S^2_{E} \tag{3.17}\] podemos decir que:
La variabilidad total (en la muestra) (varianza Y) es igual a la variabilidad explicada por el modelo (varianza de \(Y^*\)) mas la variabilidad no explicada (varianza residual o de los errores)
En un curso más avanzado veremos que un estimador de la varianza de los errores \(\sigma^2\) podría ser la varianza residual: \(\hat{\sigma}^2=\frac{\sum e_i^2}{n-1}\). Sin embargo, este estimador es sesgado, por lo que en la inferencia del modelo de regresión se utiliza como estimador \(\hat{\sigma}^2=\frac{\sum e_i^2}{n-2}\), que es insesgado.
Ejemplo 3.6 Vamos a comprobar la relación dada en la Ecuación 3.15 o, equivalentemente, en la Ecuación 3.17.
Partimos de las tablas de cálculo construidas en los ejemplos 3.1. y 3.5. Recordemos que hemos estimado el modelo: \[Eficiencia^*=35.0404 + 3.1633\cdot Edad\] Con toda esta información, vamos a calcular la varianza de la eficiencia (varianza total de la variable dependiente), la varianza de la regresión (varianza de los valores teóricos) y la varianza residual (varianza de los errores).
Solución:
Partimos de los cálculos recogidos en la Tabla 3.2 y Tabla 3.3 que se reproducen en la Tabla 3.4.
| X: Edad | Y: Eficiencia | \(y_i^2\) | \(x_i \cdot y_i\) | \(y^*_i\) | \(e_i\) |
|---|---|---|---|---|---|
| 5 | 50 | 2,500 | 250 | 50.8569 | -0.8569 |
| 10 | 72 | 5,184 | 720 | 66.6734 | 5.3266 |
| 12 | 70 | 4,900 | 840 | 73 | -3 |
| 15 | 78 | 6,084 | 1,170 | 82.4899 | -4.4899 |
| 18 | 95 | 9,025 | 1,710 | 91.9798 | 3.0202 |
| — | — | — | — | — | |
| \(\sum=365\) | \(\sum=27,693\) | \(\sum=4,690\) | \(\sum=365\) | \(\sum=0\) |
Con los resultados de la Tabla 3.4 teníamos, junto con los valores observados de la variable dependiente (\(y_i\)), los valores de las eficiencias teóricas calculadas a partir del modelo estimado (\(y^*_i\)) y los errores (\(e_i=y_i-y^*_i\)). Con los valores de las variables \(Y\), \(Y^*\) y \(E\) calculamos sus medias en el ejemplo 3.5: \[\overline{y}=\overline{y}^*=73 \qquad \overline{e}=0\] En la Tabla 3.5 calculamos las diferentes sumas de cuadrados:
- \(SCT=\displaystyle\sum_{i=1}^n(y_i - \overline{y})^2\) en la columna 2
- \(SCR=\displaystyle\sum_{i=1}^n(y_i^* - \overline{y}^*)^2\) en la columna 4
- \(SCE=\displaystyle\sum_{i=1}^n e_i^2\) en la columna 5.
| \(y_i-\overline{y}\) | \((y_i-\overline{y})^2\) | \(y^*_i-\overline{y}*\) | \((y^*_i-\overline{y}^*)^2\) | \(e^2_i\) |
|---|---|---|---|---|
| -23 | 529 | -22.1431 | 490.317 | 0.734 |
| -1 | 1 | -6.3266 | 40.026 | 28.366 |
| -3 | 9 | 0 | 0 | 9 |
| 5 | 25 | 9.4899 | 90.058 | 20.159 |
| 22 | 489 | 18.9798 | 360.233 | 9.120 |
| — | — | — | ||
| \(SCT=1,048\) | \(SCR=980.633\) | \(SCE=67.367\) |
Sumando las respectivas columnas obtenemos que: \[SCT = 1,048 \qquad SCR =980.633 \qquad SCE = 67.367\] Se satisface la Ecuación 3.15: \[SCT=SCR+SCR \quad \rightarrow SCT=980.633+67.367=1,048\] Si dividimos las sumas de cuadrados por el tamaño de la muestra (o población, según el caso), obtenemos las correspondientes varianzas: \[S^2_Y=\frac{SCT}{n}=\frac{1,048}{5}=209.6 \qquad S^2_{Y^*}=\frac{SCR}{n}=\frac{980.633}{5}=196.1266 \qquad S^2_E=\frac{SCE}{n}=\frac{67.367}{5}=13.4734\] Por tanto: \[S^2_Y=S^2_{Y^*}+S^2_E=196.1266+13.4734=1,048\]
3.6 Análisis de la bondad del ajuste
Una vez hemos estimado el modelo es hora de proceder a su evaluación. Pretendemos determinar la calidad o bondad del modelo para conocer la fiabilidad de las predicciones que proporcionemos basadas en él. Cuanto mejor sea el ajuste del modelo, mayor será la fiabilidad de la predicción/ pronóstico/estimación que realicemos.
Para el adecuado seguimiento de este apartado, tener siempre presente las relaciones que comentamos en la Sección 3.5:
- La suma de los cuadrados totales (SCT) es igual a la suma de los cuadrados explicados por la regresión (SCR) más la suma de los cuadrados de los errores/residuos (SCE): \(SCT = SCR + SCE\)
- La variabilidad total (varianza Y) es igual a la variabilidad explicada por el modelo (varianza de \(Y^*\)) mas la variabilidad no explicada (varianza residual o de los errores)
Podemos pensar en la varianza de los errores/residuos, a la que denominamos varianza residual (\(S^2_E\)), como una primera medida de la bondad del ajuste. \[S^2_E=\frac{\displaystyle\sum_{i=1}^n (e_i-\overline{e})^2}{n-1} \tag{3.18}\] y como en la regresión \(\overline{e}=0\), entonces: \[S^2_E=\frac{\displaystyle\sum_{i=1}^n e_i^2}{n-1} \tag{3.19}\]
Cuanto mayor sea la varianza residual, menor será la capacidad explicativa del modelo estimado. Por el contrario, cuanto menor sea la varianza residual, menores serán los errores/residuos, mejor se ajustará la nube de puntos a una recta; por tanto, mejor será el modelo. Este comentario queda de manifiesto si observamos la Figura 3.6.
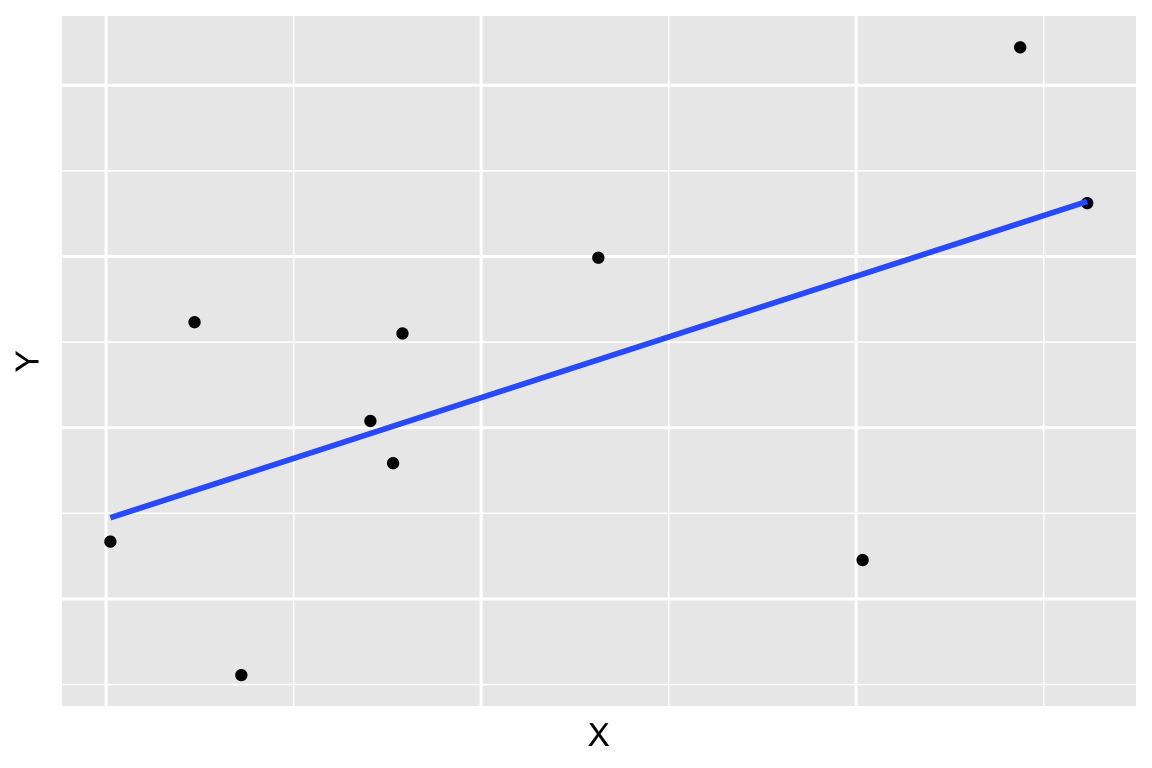
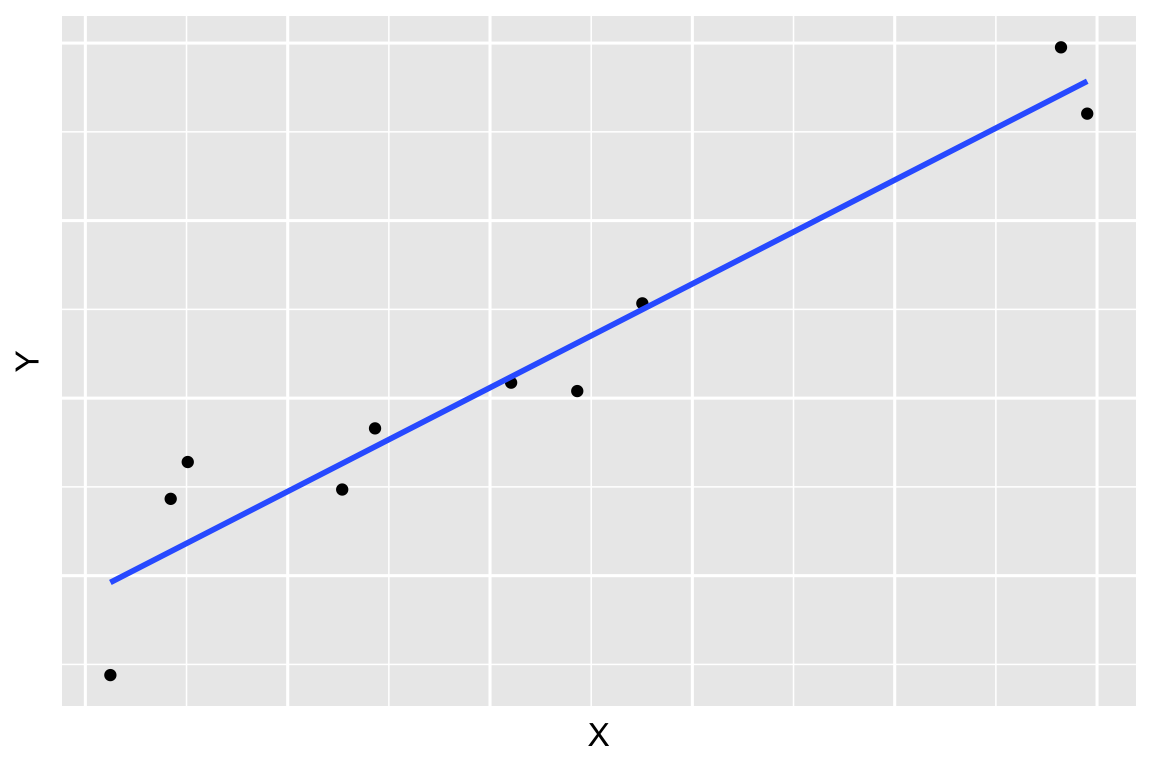
Sin embargo, la varianza residual presenta dos problemas. Por una parte, esta claro que si la varianza residual vale cero (\(S^2_e=0)\) el ajuste es perfecto, la nube de puntos se ajustará perfectamente a una recta; pero, ¿a partir de qué valor se puede considerar que la varianza residual es grande o pequeña y, por tanto, la calidad del ajuste realizado es bueno o malo? Por otra parte, la varianza residual, como varianza, depende de las unidades de medida en que viene expresada la variable. Por estos motivos, se define una medida adimensional, a la que no le afectan los cambios de unidad y cuyo valor se encuentra acotado, lo que facilita su interpretación. Este medida se conoce como coeficiente de determinación, y se denota por \(R^2\).
El coeficiente de determinación se define como la proporción de la variabiliad total (varianza Y) que viene explicada por el modelo (varianza de Y\(^*\))de la variable dependiente (\(Y\)) que viene explicada por el modelo estimado. \[R^2=\frac{S^2_{Y^*}}{S^2_Y} \tag{3.20}\]
El coeficiente de determinación se encuentra acotado, de forma que:
\[0 \leq R^2 \leq 1 \tag{3.21}\]
Interpretación del coeficiente de determinación
Si \(R^2=1\), entonces el ajuste es perfecto, toda la variabilidad de Y es explicada por la regresión, por el modelo:
\[S^2_Y=S^2_{Y^*}\quad y \quad S^2_{e}=0\]Si \(R^2=0\), entonces el ajuste es nulo, toda la variabilidad de Y es explicada por los residuos:
\[S^2_Y=S^2_{e}\quad y \quad S^2_{Y^*}=0\]Cuanto mayor sea \(R^2\) mejor será el ajuste, más fiables las predicciones generadas a partir del modelo estimado.
De acuerdo con Casas-Sánchez y Santos-Peñas (1995), se puede considerar que el ajuste es bueno si el valor del coeficiente de determinación es mayor o igual a 0.75.
No obstante, según Newbold, Carlson, y Thorne. (2010): se ha encontrado que para modelos basados en datos de series temporales el coeficiente de determinación es 0.80 o superior, en modelos con datos de corte transversal el \(R^2\) toma valores entre 0.4 y 0.6, y en modelos basados en datos provenientes de individuos con frecuencia tienen un \(R^2\) en el rango 0.10-0.20”
3.6.1 Otras expresiones del coeficiente de determinación
En ejercicios de carácter teórico-práctico, el coeficiente de determinación puede obtenerse de distintas maneras dependiendo de los datos que tengamos disponibles. Así, por ejemplo, si partimos de la matriz de varianzas-covarianzas, es conveniente recordar la siguiente relación:
\[R^2=\frac{S^2_{Y^*}}{S^2_Y}=\frac{S^2_{XY}}{S^2_X\cdot S^2_Y} \tag{3.22}\]
A su vez, de la expresión anterior se deduce:
\[R^2=\frac{S^2_{XY}}{S^2_X\cdot S^2_Y}= \left( \frac{S_{XY}}{S_X \cdot S_Y}\right)^2= r^2_{XY} \tag{3.23}\]
El coeficiente de determinación es igual al coeficiente de correlación lineal al cuadrado únicamente en la regresión lineal simple.
Por último, consideremos la igualdad: \[S^2_Y=S^2_{Y^*}+S^2_E \tag{3.24}\] dividiendo la expresión anterior por \(S^2_Y\): \[\frac{S^2_Y}{S^2_Y}=\frac{S^2_{Y^*}}{S^2_Y}+\frac{S^2_E}{S^2_Y}\]
Así: \[1=R^2+\frac{S^2_E}{S^2_Y}\] y despejando \(R^2\): \[R^2= 1-\frac{S^2_e}{S^2_Y} \tag{3.25}\] donde: \(\displaystyle\frac{S^2_E}{S^2_Y}\) es la proporción de la varianza de Y que no es explicada por la regresión sino por los residuos; es una varianza residual relativa, respecto de la varianza total.
Para evaluar la bondad de un ajuste no se utiliza únicamente el coeficiente de determinación sino que se acompaña de otras medidas, las estudiaremos en la materia de Inferencia estadística.
Ejemplo 3.7 Un estudio realizado en una misma fecha en 8 países europeos fuera de la zona euro ha encontrado una correlación entre la prima de riesgo (variable Y, expresada en puntos básicos) y el déficit público (variable X, expresada en porcentaje) igual a 0.635. Adicionalmente, contamos con los siguientes estadísticos descriptivos:\[\overline{x}=4.3125 \quad \overline{y}=156.25 \quad S^2_X=0.2036 \quad S^2_Y=19.8\] Estima el modelo de regresión que permita analizar el efecto del déficit público sobre la prima de riesgo y valora la calidad del mismo.
Solución: Tenemos que estimar el modelo lineal: \[\text{prima.riesgo}{^*_i}=a+b\cdot \text{déficit.público}_i\quad \rightarrow \quad y^*_i=a + b\cdot x_i\] donde, como ya sabemos, \(a=\overline{y}-b\cdot \overline{x}\quad y \quad b=\displaystyle\frac{S_{XY}}{S^2_X}\)
Calculamos primero \(b\) para después calcular \(a\), pero antes necesitamos conocer el valor de la covarianza. En el enunciado del ejercicio nos dicen que la correlación entre las variables es 0.635, así: \[r_{XY}=\frac{S_{XY}}{S_X \cdot S_Y} \quad \rightarrow \quad S_{XY} = r_{XY}\cdot S_X \cdot S_Y = 0.635 \cdot \sqrt{0.2036} \cdot \sqrt{19.8}\] \[S_{XY}\approx1.275\hspace{1mm}(\text{porcentaje}\cdot \text{puntos básicos})\] que nos indica que, en media, una mayor déficit público se asocia con una mayor prima de riesgo.
Conocido el valor de la covarianza ya estamos en disposición del calcular el coeficiente de regresión: \[b=\frac{S_{XY}}{S^2_X}=\frac{1.275}{0.2336}=6.26223\]
y utilizando este resultado obtenemos el valor de la ordenada en el origen (recordad, también se denomina a este parámetro: intercepto, constante, intersección.) \[a=\overline{y}-b\cdot \overline{x}=156.25-6.2623\cdot 4.3125\approx 129.2424\]
El modelo que hemos estimado es: \[\text{prima.riesgo}{^*_i}=129.2424+6.2623\cdot \text{déficit.público}_i\] Estimamos que un incremento de un 1% en el déficit público producirá, en promedio, un incremento de 6.2623 puntos porcentuales de la prima de riesgo.
Para evaluar la capacidad predictiva del modelo que hemos estimado calculamos el coeficiente de determinación. \[R^2 = \frac{S^2_{XY}}{S^2_X\cdot S^2_Y}=\frac{1.275^2}{0.2036\cdot 19.8}\approx0.4032\] pero también sabemos que en el caso lineal: \[R^2 = r^2_{XY}=0.635^2\approx 0.4032\] Este resultado podemos interpretarlo como: el 40.32% aproximadamente de la variabilidad de la prima de riesgo es explicada por su dependencia lineal con el déficit público. Recordemos que para interpretar el \(R^2\) centramos la atención en la definición: \(R^2=\displaystyle\frac{S^2_{Y^*}}{S^2_Y}\)
Entonces, ¿el ajuste es bueno? El ajuste es moderadamente bueno, sería mejor si se aproximara más el valor a 1 y peor si lo hiciera a 0. En un curso de Inferencia estadística veríamos que podemos obtener coeficientes de determinación bajos pero estimaciones de los coeficientes (\(a\) y \(b\) en el caso de la regresión simple) estadísticamente significativos, con lo que seguimos obteniendo una información importante.
El déficit público es cuando un estado atiende más gastos que ingresos genera. El déficit público se financia con deuda (pública). En este enlace puede consultarse la deuda de los países: consultar deuda La prima de riesgo es el sobreprecio que tienen que pagar los países para poder obtener financiacion. También se le conoce como “riesgo país”. En este enlace puede consultarse la prima de riesgo de los países: consultar prima de riesgo
Ejemplo 3.7. con Excel. En el ejemplo 3.1. con Excel hemos calculado una estimación de los coeficientes del modelo de regresión utilizando las funciones de Excel: INTERSECCION.EJE() y PENDIENTE(). Vamos a extender aquel ejemplo y vamos a introducir la función ESTIMACION.LINEAL(), que nos devolverá el valor de los dos coeficientes, y también calcularemos la capacidad predictiva del modelo con la función COEFICIENTE.R2().
Abrimos el fichero ej-3-1.xlsx.
En la celda J10 escribimos Estimación modelo y en la celda J13 el texto Coeficiente determinación.
Nos situamos en la celda J11 e introducimos la fórmula: =estimacion.lineal(B2:B6;A2;A6), el primer resultado que devuelve es la estimación del coeficiente de regresión (parámetro b) y el segundo la estimación de la constante (parámetro a). En la celda J14 ejecutamos la fórmula: coeficiente.r2(B2:B6;A2;A6). El coeficiente de determinación es aproximadamente 0.9257 o el 92.57%, es decir, el 92.57% de la variablidad de la eficiencia viene explicada por su dependencia lineal con la edad de contitución de la empresa. En consecuencia, el ajuste realizado tiene una alta capacidad predictiva, es un muy buen ajuste. La apariencia final de la hoja Excel debería ser similar a la Figura 3.7.
Guardad el fichero de trabajo con el nombre ej_3_7.
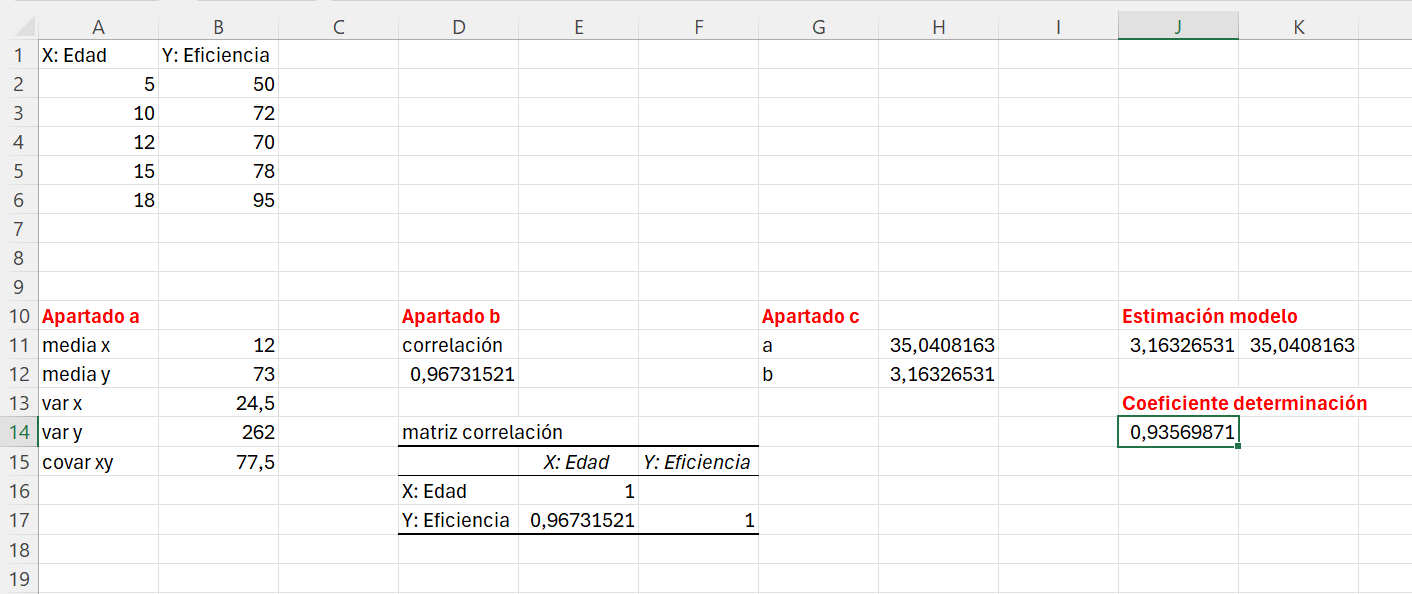
Puedes seguir los pasos de resolución del ejemplo en la animación que se encuentra en [https://www.uv.es/ticstat/ej_3_7_excel.gif](https://www.uv.es/ticstat/ej_3_7_excel.gif)
3.7 Predicción
La finalidad del análisis de regresión (simple) es predecir/pronosticar el valor de la variable dependiente (\(Y\)) a partir de un valor dado de la variable independiente (\(X\)).
Partimos del modelo estimado de \(Y/X\): \[Y^*=\overline{y}+\frac{S_{XY}}{S^2_X}\cdot (X-\overline{x})\] de forma que obtendremos una predicción individual al sustituir en el modelo estimado un valor específico \(x_0\) de la variable \(X\). Esto es: \[y^*_0=\overline{y}+\frac{S_{XY}}{S^2_X}\cdot (x_0-\overline{x}) \tag{3.26}\]
En Inferencia estadística se estudia cómo obtener intervalos de confianza para la predicción puntual y para el valor medio (predicción de la esperanza condicionada).
Ejemplo 3.8 A partir del modelo estimado en el Ejemplo 3.7, da un pronóstico de la prima de riesgo esperada para un país con un déficit público del 5.6%
Solución: Si el déficit público es del 5.6% (\(x_0=5.6\)), basándonos en el modelo que hemos estimado: \[\text{prima.riesgo}{^*_i}=129.2424+6.2623\cdot \text{déficit.público}_i \qquad (R^2=0.4032)\] nuestro pronóstico para la prima de riesgo dada sería: \[\text{prima.riesgo}^*_0=129.2424+6.2623\cdot5.6=164.3113 \hspace{1mm}\text{puntos básicos}\]
Ejemplo 3.8 con Excel. Para generar pronósticos disponemos de varias funciones en Excel: PRONOSTICO.LINEAL() y TENDENCIA(). Con la primera función sólo podemos generar pronósticos para una valor dado de X; con la segunda función podemos hacerlo para más de un valor de X.
La función PRONOSTICO.LINEAL tiene tres argumentos. El primero, el argumento x, se refiere al valor \(x_0\) para el que vamos a generar el pronóstico. Los dos restantes argumentos con conocido_y y conocido_x.
Abrimos el fichero ej_3_7.xlsx.
Queremos estimar la eficiencia de una empresa que tiene 13 años de antigüedad.
Comprobamos que el valor 13 se encuentra dentro del rango de valores relevantes de la variable Edad. Recordad que el modelo lo hemos estimado para un determinado rango de valores de la variable independiente.
Nos situamos en la celda J16 y escribimos Pronóstico. En la celda J17 intoducimos la fórmula: =pronostico.lineal(13,B2:B6;A2:A6). Para una empresa con 13 años de antigüedad estimamos una eficiencia productiva de 76.16 puntos porcentuales.
¿Es fiable nuestro pronóstico?
En el ejemplo 3.7 con Excel concluíamos que el modelo estimado tenía una alta capacidad explicativa, el coeficiente de determinación era 0.9257. Por tanto, siempre que nos movamos dentro del rango de valores de la variable X, que es para el que se observa una relación lineal, podemos decir que nuestro pronóstico es muy fiable.
Otra cuestión sería si generásemos un pronóstico de eficiencia para una empresa con una antigüedad de, por ejemplo, 25 años. No sabemos cómo evoluciona la relación entre eficiencia y edad por encima de 18 años (o por debajo de 5).
Guardad el fichero de trabajo con el nombre ej_3_8.
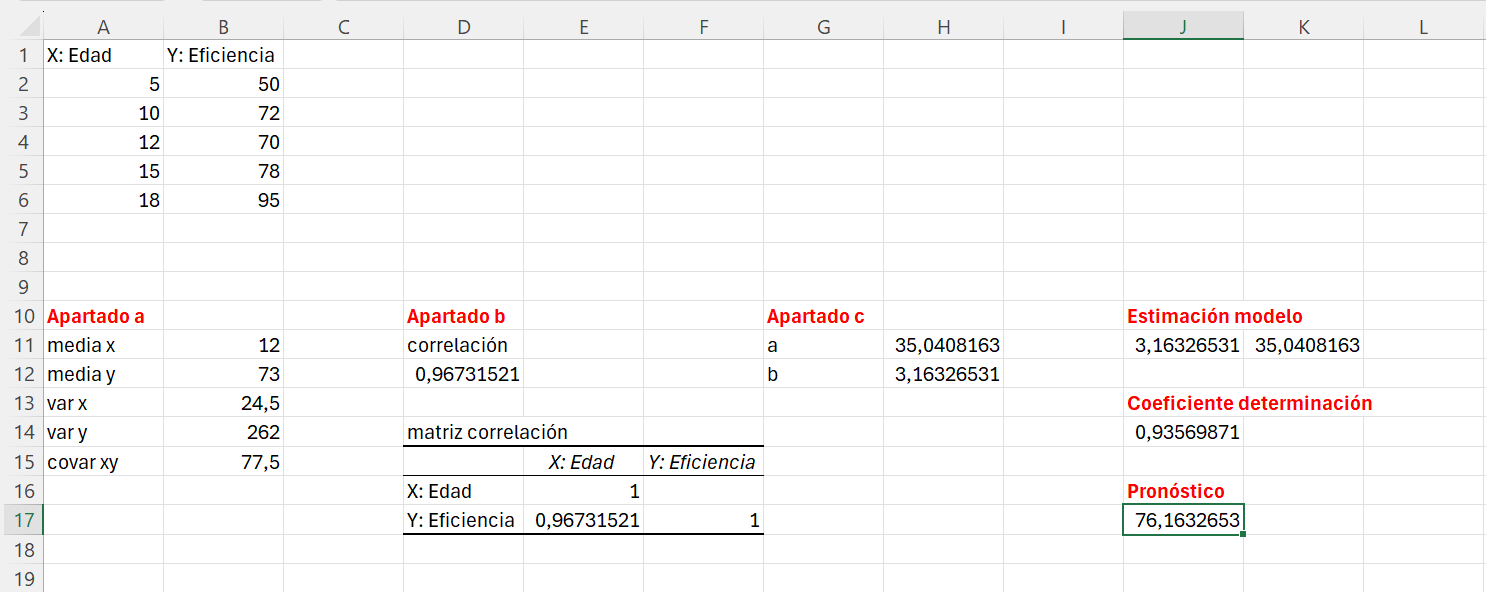
Puedes seguir los pasos de resolución del ejemplo en la animación que se encuentra en [https://www.uv.es/ticstat/ej_3_8_excel.gif](https://www.uv.es/ticstat/ej_3_8_excel.gif)
3.8 Regresión con Excel
Antes de proceder al análisis estadístico existe todo un proceso de trabajo cuyo objetivo es asegurar que los datos con los que vamos a trabajar sean, por decirlo de alguna manera, útiles. Este proceso suele denominarse limpieza (cleaning data) y ordenación de los datos (tidy data).
La limpieza de datos consiste en identificar y corregir errores en los datos. Esto incluye detectar observaciones anómalas (datos que no siguen el patrón esperado), tratar datos faltantes (missing data), eliminar casos repetidos, entre otros. Un conjunto de datos limpio es esencial para evitar conclusiones erróneas.
Una vez que los datos están limpios, es importante organizarlos de manera que sean más fáciles de analizar. Esto puede implicar transformar variables existentes, crear nuevas variables que nos interesen, seleccionar casos específicos para el análisis, o codificar/recodificar variables cualitativas. Este paso también se conoce como proceso de ordenación de datos.
Con los datos limpios y organizados, podemos proceder al análisis estadístico que nos permitirá extraer la información útil contenida en los datos. Comenzamos con una exploración inicial, que incluye la creación de tablas de frecuencias y la elaboración de gráficos sencillos pero muy útiles, como diagramas de barras, histogramas, polígonos de frecuencias y diagramas de dispersión. Estos gráficos nos permiten visualizar cómo se distribuyen las variables y si existe algún tipo de asociación/relación entre ellas. Básicamente, en esta etapa aplicamos los contenidos estudiados en los dos primeros capítulos.
Seguidamente, dependiendo de los objetivos del análisis, podemos aplicar diferentes técnicas estadísticas. En este manual nos hemos centramos en este capítulo en la regresión lineal simple, que es una técnica básica para entender la relación entre dos variables. Sin embargo, si comprendes bien este concepto, la extensión a la regresión lineal múltiple resulta mucho más sencilla; y estos modelos son ampliamente utilizados porque son eficaces y fáciles de aplicar.
Finalmente, a partir de las conclusiones que extraigamos de nuestros análisis emitiremos el oportuno informe, en el que incluiremos los principales resultados obtenidos, tanto numéricos como gráficos, con sus correspondientes interpretaciones.
Ahora, vamos a realizar un ejemplo completo de regresión. Descargad el conjunto de datos que se encuentra en www.uv.es/ticstat/regresion.xlsx. Una vez descargado el fichero en vuestra directorio de trabajo, abridlo. Los datos se refieren a los ingresos (en euros) y consumo (en euros) de una muestra de 100 familias. Los datos han sido simulados con la única finalidad de practicar algunos de los conceptos explicados en este manual. En la Figura 3.9 se muestran las primeras 20 observaciones.
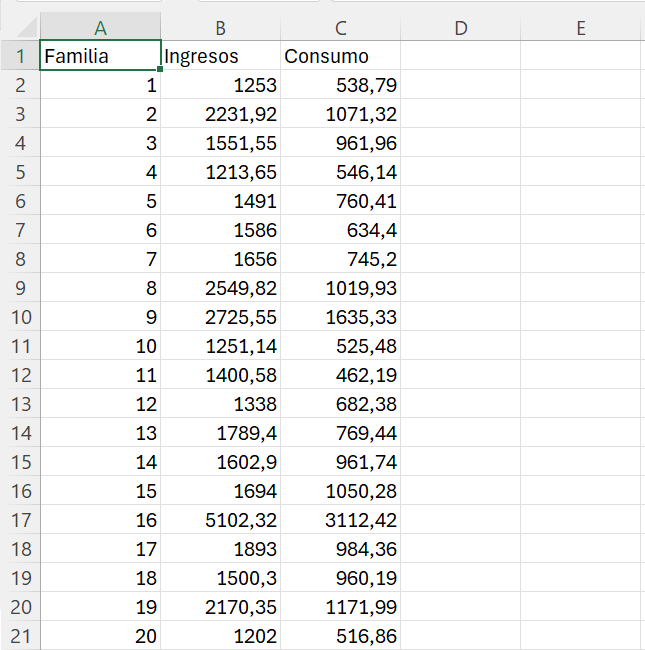
Obtenemos un resumen descriptivo de las variables utiizando la herramienta de análisis de datos. Seleccionamos como rango de entrada de datos el rango B1:C101. Marcamos Rótulos en la primera fila y Resumen estadísticas, como rango de salida fijamos la celda F1. Los resultados que obtenemos se muestran en la Figura 3.10.
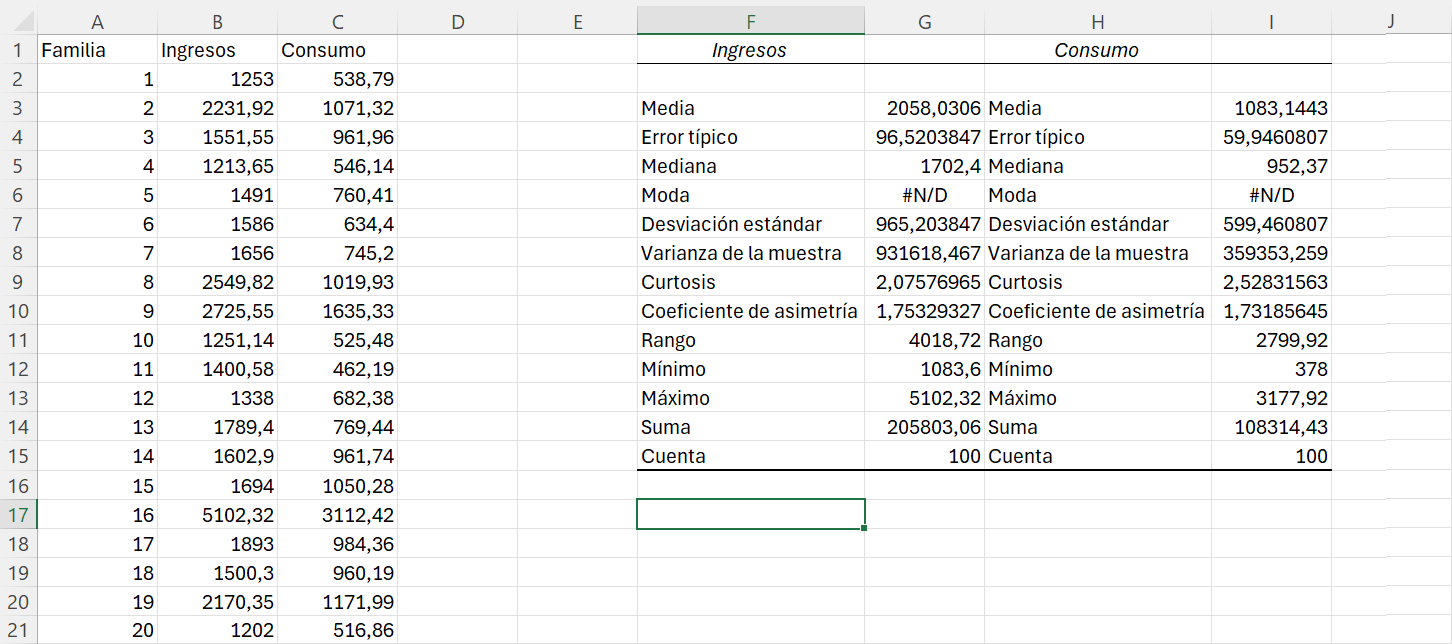
Observad que al seleccionar como rango de datos más de una variable, el resumen descriptivo se realiza para cada una de las variables seleccionadas, no tenemos que hacerlo una a una.
Las familias de la nuestra analizada tienen unos ingresos medios de 2,058.06 euros y el consumo medio es de 1,083.14 euros, lo que representa aproximadamente el 52.63% de los ingresos.
Excel nos devuelve #ND (no disponible) en la moda tanto de ingresos como de gastos. Esto es porque no hay ningún valor que se repita, todos los valores tienen la misma frecuencia.
En la función Estadística descriptiva de análisis de datos la moda es calculada con la función MODA.UNO(), con lo que únicamente devuelve un valor. Sin embargo, como ya sabemos, la moda no es única, una variable puede presentar varias modas. En este sentido, es conveniente que calculemos la moda con la función MODA.VARIOS().
El ingreso mediano de las familias es de 1,702,04 euros, es decir, aproximadamente el 50% de las familias consideradas tienen unos ingresos por debajo de 1,702.04 euros. Por ejemplo, sería interesante conocer los deciles de los ingresos para tener una ídea de su distribución.
El consumo mediano es de 952,37 euros.
El ingreso mediano es menor que el ingreso medio. También ocurre lo mismo con el consumo mediano y el consumo medio. La media, en ambos casos, se desplaza a la derecha como consecuencia de ingresos/consumos altos. También, tanto para los ingresos como para el consumo, la distribución es asimética positiva (coeficiente de asimetría positivo, cola derecha) y mas apuntada que la normal (coeficiente de curtosis mayor que cero, lo interpretamos según la Ecuación 1.26). Esto nos da una idea de que la mayor parte de las familias se encuentran en los niveles más bajos de ingresos/consumo; cuanto mayores son los ingresos/consumo, menos familias hay.
Con esta imagen sobre la forma de la distribución de ingresos vamos a construir un histograma. Como haríamos los propio con el consumo familiar (o con cualquier otra variable que tuviésemos en nuestro conjunto de datos), vamos a crear el histograma utilizando las tablas dinámicas. Pero antes de esto, necesitamos saber cúanto intervalos vamos a crear y cúal va a ser su amplitud. Respecto a la primera cuestión, vamos a construir 10 intervalos (\(k=\sqrt{n}=\sqrt{100}=10\)). En cuanto a la amplitud, será el resultado de dividir el rango de los ingresos entre el número de intervalos; por tanto, los intervalos tendrán amplitud: \(4,018.72/10=401.872\)
Sabiendo esto, creamos la tabla dinámica:Insertar>Tabla dinámica>De una tabla o rango. Seleccionamos como rango el rango B1:C101 y colocamos la tabla dinámica en la celda K1. Al clicar en Aceptar se creará la tabla dinámica y se abrirá el cuadro de Campos de tabla dinámica.
Arrastramos Ingresos a filas y a valores. Como no queremos la *Suma de Ingresos sino que estamos interesados en cuantás familias (Recuento) hay para cada nivel de ingresos, hacemos clic sobre Suma de Ingresos y seleccionamos Configuración de campo de valor..>Recuento>Aceptar**.
Tenemos la tabla de frecuencias de los Ingresos. Como se comentó en el capítulo 1, no hacemos un diagrama de barras/columnas porque la variable ingresos es continua, pero aún considerando su posible discretización, presenta muchos distintos valores, el diagrmama de barras no aportaría información de interés.
Para construir el histograma, nos situamos sobre cualquier celda de la etiqueta de fila de la tabla dinámica y hacemos clic en el botón derecho, seleccionamos Agrupar…. Por defecto de fijan los valores mínimo y máximo de los ingresos como valores de las casillas Comenzar en y Terminar en, respectivamente. En la casilla Por introducimos el valor de nuestra amplitud de intervalos: 401.872. Al clicar en Aceptar se construye la tabla de valores agrupados (en intervalos) de los ingresos.
Construimos el histograma a partir de un diagrama de barras/columna. Seleccionamos Insertar > Insertar gráfico de columnas o de barras y clicamos sobre el primer gráfico de Columna en 2-D. Se abre el Área de gráfico y las opciones de Diseño de gráfico. Es el momento de seleccionar el origen de los datos a representar. Como rango de datos del gráfico marcamos el rango L2:L11 que es donde se encuentran las frecuencias de cada uno de los intervalos; por defecto se seleccionará como Etiquetas del eje horizontal los intervalos. Hacemos clic en Aceptar para terminar el gráfico.
Como vemos, tenemos un diagrama de barras. Como hicimos en su momento (ver Sección 1.3.2), transformamos el diagrama de barras en un histograma seleccionando cualquier barra del dibujo, haciendo doble clic en el botón derecho del ratón y seleccionando la opción Dar formato a serie de datos…. En Opciones de serie cambiamos el Ancho del rango al 0%. Cambiamos el color de relleno y de la línea, eliminamos las líneas de cuadrícula y el eje vertical primario, añadimos las etiquetas de datos, proporcionamos tíulo al eje horizontal y al gráfico. Agrandamos (de forma proporcional) un poco el dibujo pinchando sobre el gráfico y clicando sin soltar sobre una equina arrastrando diagonalmente. Nuestro histograma será similar al de la Figura 3.11.
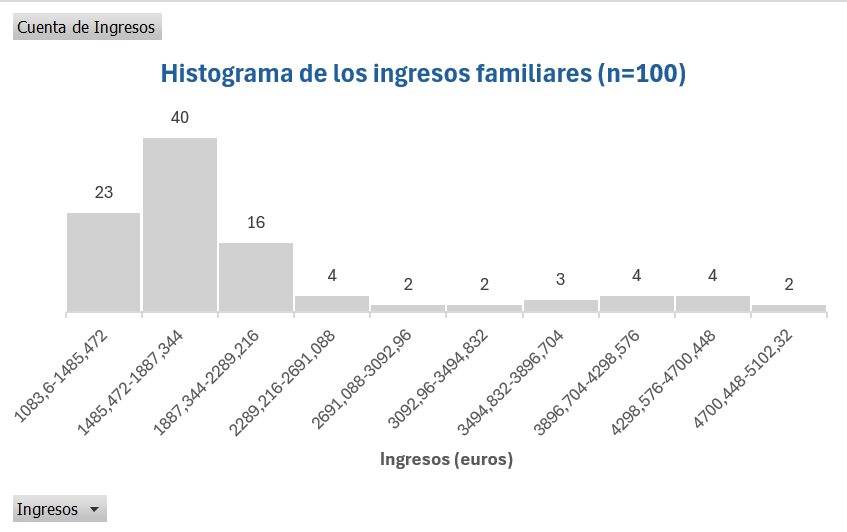
¿Existe alguna relación entre ingresos de la familia y su consumo?
Vamos, en primer lugar, a dibujar un diagrama de dispersión para ver si la nube de puntos que obtengamos nos proporciona alguna información.
En el diagrma de dispersión, ¿qué variable colocamos en el eje X (horizontal) y qué variable en el eje Y (eje vertical)? Nos preguntamos, el consumo influye en los ingresos o son los ingresos los que influyen en el consumo? La segunda, verdad, pues la variable ingresos la situaremos en el eje X y la variable consumo en el eje Y.
En el Ejemplo 2.7 con Excel vimos como construir un diagrama de dispersión. Repasa aquel ejemplo y construye el gráfico de dispersión, debería ser similar a la Figura 3.12, y colócalo para que comience en la celda F37.
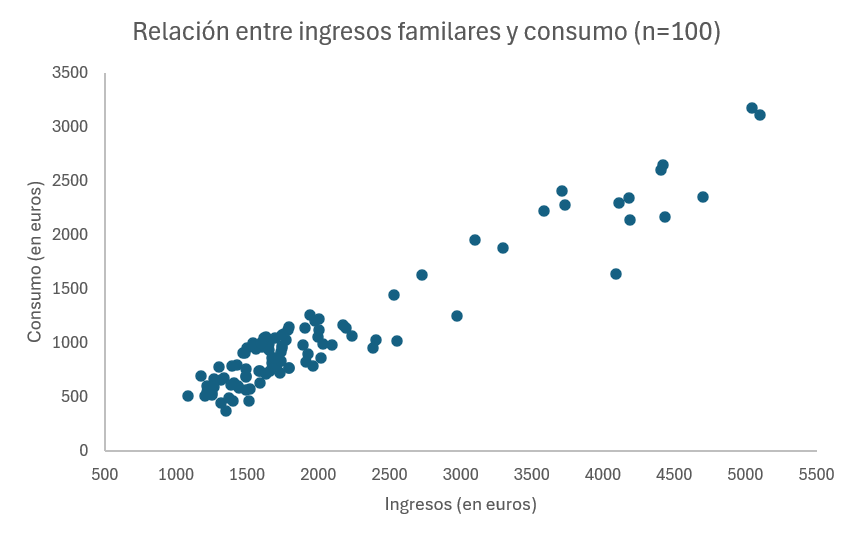
Interpretamos la nube de puntos del gráfico. Observad que tenemos muchos puntos (familias) en los niveles bajos/medios de ingresos/consumos, como comentamos en el histograma. Según la forma de nuestro gráfico de dispersión, como punto de partida podemos asumir una relación lineal entre ingresos y consumo, positiva porque la nube de puntos es ascendente (la covarianza será positiva) y bastante fuerte porque los puntos no parecen alejarse mucho de una hipotética recta, con lo que se espera un coeficiente de correlación alto.
Para corrobar esta impresión que nos hemos hecho de la observación del diagrama de dispersión, calculamos la covarianza y la correlación. Lo hacemos en las celdas O1 y O2, respectivamente.
La covarianza es 551,881.396. ¿Es alta la covarianza entre ingresos y consumo? Recuerda que de la covarianza interesa el signo, no el valor que toma. El signo nos indica la dirección de la variación conjunta de las variables. Como la covarianza es positiva interpretamos que, en media, cuanto mayores son los ingresos de las familias, mayor es también su consumo.
Si estamos interesados en calificar la intensidad de la relación lineal, lo hacemos en base al resultado del coeficiente de correlación. Así, al comentario realizado en el interpretación de la covarianza añadiríamos que la relación lineal entre ingresos y consumo es muy fuerte, puesto que la correlación entre ambas toma un valor muy elevado, concretamente 0.9538
Cuando calculamos la correlación lo que queremos es evaluar la fortaleza de la relación lineal entre dos variables. En cambio, con la regresión lo que hacemos es estimar la estructura funcional de la relación entre dos variables ajustando a una determinada función. Cuando ajustamos a una recta, como hemos visto en este capítulo, tenemos un modelo de regresión lineal.
En nuestro ejemplo, y dado que observamos una relación lineal entre ingresos y consumo, vamos a estimar el siguiente modelo:\[consumo_i=a+b\cdot ingresos_i\] Para estimar el modelo podemos utilizar las funciones vistas en el capítulo. Sin embargo, en este ejemplo vamos a recurrir a la función Regresión de la herramienta de Análisis de datos de Excel.
Seleccionamos: Datos > Análisis de datos > Regresión. Como se ilustra en la Figura 3.13, en el cuadro de Regresión indicamos el rango C1:C101 como el Rango Y de entrada porque el consumo es la variable dependiente. En *Rango X de entrada introducimos el rango B1:B101, que son los ingresos y es la variable independiente. Marcamos Rotulos en primera línea. Como rango de salida seleccionamos la celda L16, Excel devolverá los resultados de la regresión a partir de esta celda. Por último, en Residuales marcamos Residuos, Residuos estándares y Curva de regresión ajustada**.
Excel facilita muchos resultados de la regresión (ver Figura 3.14); sin embargo, gran parte de ellos corresponde a la inferencia del modelo, que no son abordados en este manual introductorio.
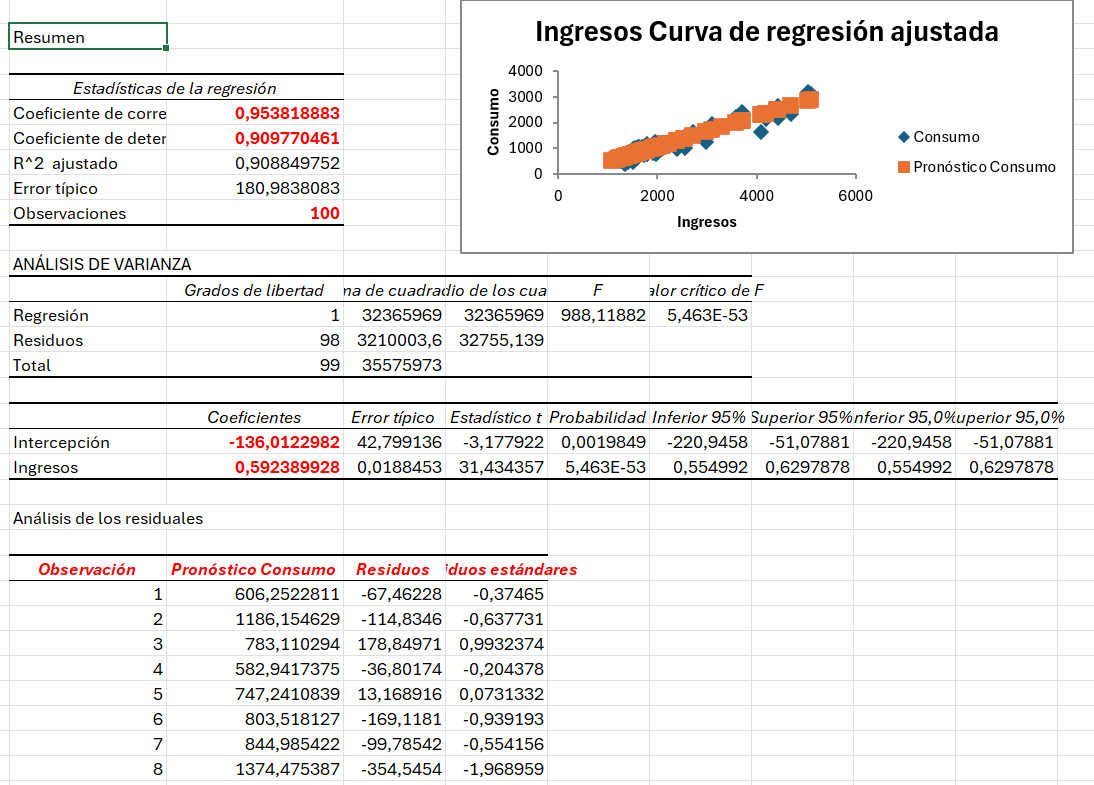
En el apartado Estadísticas de la regresión tenemos el coeficiente de correlación, el coeficiente de determinación y el número de observaciones. El $R^2, que como sabemos nos informa de la capacidad explicativa del modelo estimado, es aproximadamente 0.9098. Es decir, el 90.98% de la variablidad del consumo de las familias analizadas viene explicado por su dependencia lineal con los ingresos. El ajuste que hemos realizado es, por tanto, muy bueno, el modelo tiene una muy alta capacidad explicativa.
El valor de la constante (intercepción) es -136.0123, lo que nos literalmente indica que si los ingresos de la familia es cero euros, se espera que su consumo sea de -136.0123 euros. Desde un punto de vista económico, en este sencillo modelo de regresión el valor de a representa el consumo autónomo y se considera que este consumo es positivo. No obstante, en este ejemplo hemos obtenido un valor negativo para el consumo autónomo, lo que carece de sentido económico.
El coeficiente de regresión de los ingresos toma el valor 0.5924. En economía este coeficiente se refiere a la denominada propensión marginal a consumir. Si los ingresos de las familias se incrementa en 1 euro, se espera que el consumo se incremente (el coeficiente es positivo) en 0.59 euros aproximadamente. Como son valores bajos suele aumentarse la escala, es decir, si los ingresos de las familias se incrementan en 100 euros, se espera que el consume se incremente en 59.24 euros.
La función de gasto en consumo fue propuesta por Keynes y la desarrolló en su libro “Teoría general del empleo, el interés y el dinero”. Keynes consideró gasto en consumo y renta disponible.
También disponemos como resultados de la regresión: los pronósticos de consumo, los residuos y los residuos estánderes. Los pronósticos de consumo son los valores teóricos/estimados del consumo (\(Y\)); los residuos son los errores, la diferencia entre los valores observados de consumo (\(Y\)) y los pronosticados (\(Y\)); los residuos estánderes son los residuos tipificados a media cero y desviación típica 1.
Por último, como hemos marcado la casilla correspondiente a Curva de regresión ajustada, tenemos un gráfico de dispersión en el que se representan los valores observados de ingresos y consumo (\(x_i,y_i\)), así como los pares de ingresos y consumo pronosticado (\(x_i,y_i^\text{*}\)).
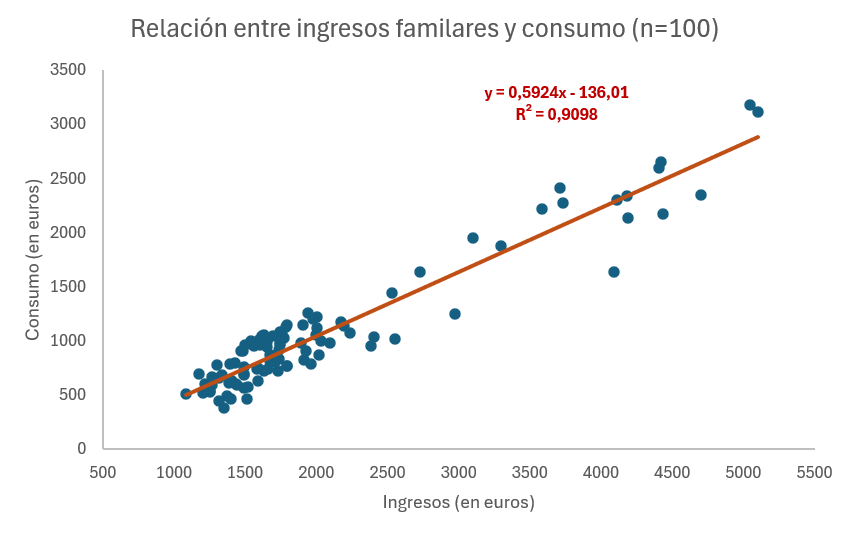
En lugar de quedarnos con este gráfico, lo que vamos a hacer para terminar con este ejemplo es añadir a nuestro diagrama de dispersión la recta de regresión estimada, así como información relavante de la misma. Clicamos sobre cualquier punto de nuestro gráfico, hacemos clic en el botón derecho del ratón y seleccionamos la opción: Agregar línea de tendencia…. En opciones de línea de tendencia seleccionamos Lineal; también seleccionamos las casillas Presentar ecuación en el gráfico y Presentar R_cuadrado en el gráfico.
Pueden estimarse modelos de regresión en los que no hay constante. En el caso de la regresión lineal simple el modelo se especificaría como: \(Y*=b\cdot X\). En este caso, en que la constante vale cero es cuando tendríamos que seleccionar la casill Señalar intersección y fijar el valor en cero.
En la Figura 3.15 se muestra el diagrama de dispersión junto con la recta de regresión y la especión del modelo.
Guardad la hoja de cálculo del ejemplo con el nombre regresion_final.
Puedes seguir los pasos de resolución completa del ejemplo en la animación que se encuentra en [https://www.uv.es/ticstat/regresion_final.gif](https://www.uv.es/ticstat/regresion_final.gif)
3.9 Ejercicios
Ejercicio 3.1 Resolved el ejercicio 3.1 en Excel reproduciendo los cálculos realizados, no utilizando las fórmulas.
Ejercicio 3.2 Se dispone de la siguiente información relativa a la variación anual en la tasa de desempleo (variable X) y la variación anual en la tasa media de absentismo laboral por enfermedad (variable Y). \[m=\begin{pmatrix} \overline{x}=0.2 \\ \overline{y}=0 \end{pmatrix} \qquad V=\begin{pmatrix} S^2_X=1.2891 & S_{XY}=-0.2891 \\ & S^2_Y=0.1 \end{pmatrix}\] Estima la regresión lineal de la variación en la tasa media de absentismo laboral por enfermedad en función de la variación en la tasa de desempleo.
Ejercicio 3.3 A partir de la información del Ejercicio 3.2, calcula el porcentaje de la variabilidad de la variación de la tasa media de absentismo que no puede ser explicada por su dependencia lineal con la variación de la tasa de desempleo.
Ejercicio 3.4 Se ha estimado la recta de regresión de la renta disponible por hogar (variable X, en euros) y el gasto que los hogares realizan en el pequeño comercio (variable Y, en euros), obteniéndose el siguiente resultado: \[Y^* = 1.923 + 0.3815\cdot X \hspace{1cm} (R^2= 0.92)\] Interpreta, en el contexto del problema, los valores estimados para los parámetros de la regresión.
Ejercicio 3.5 Interpreta, de forma completa, el valor del coeficiente de determinación obtenido en la regresión facilitada en el Ejercicio 3.4.
Ejercicio 3.6 Calcula e interpreta los deciles de ingresos y consumo de las familias de la muestra a las que se refiere el ejemplo de la Sección 3.8.
Ejercicio 3.7 Construye el histograma del consumo de forma análoga a como se construyó el histograma de los ingresos en la Sección 3.8.
Ejercicio 3.8 En el ejerccicio 3.8 con Excel se generó un pronóstico utilizando la función PRONOSTICO.LINEAL(). Continuando con este ejemplo, utiliza la función TENDENCIA() para estimar la eficiencia productiva para empresas que se constituyeron hace 6, 8 y 17 años.
Ejercicio 3.9 Laura está realizando un informe sobre el impacto de la vivienda turística en el precio de los alquileres en la ciudad de Valencia. Para ello, dispone de las observaciones para 16 distritos de la ciudad de Valencia de las siguientes variables X e Y. Con la ayuda de un programa estadístico ha obtenido los siguientes resultados:
| Medidas | Porcentaje en 2022 de vivienda turística (variable X) | Precio alquiler en 2022,en €/m2 (variable Y |
|---|---|---|
| Medias | 1.337 | 11.031 |
| Varianzas | 1.865 | 2.566 |
| Covarianza | ? | |
| Regresión de Y respecto a X: | ||
| Coeficiente a | ? | |
| Coeficiente b | 1.024 | |
| Varianza explicada | ? | |
| Varianza no explicada | 0.610 |
- Ayuda a Laura y obtén razonadamente los valores de los 3 resultados que faltan en la tabla anterior (redondea a 3 decimales).
- ¿Qué coeficiente utilizarías para medir la relación entre el porcentaje de vivienda turística y el precio del alquiler en los distritos de Valencia? Calcúlalo e interpreta su valor.
- Indica la expresión de la recta de regresión mínimo-cuadrática de Y respecto a X e interpreta el valor de su pendiente.
- La inmobiliaria idealista.com no proporciona el precio del alquiler para el distrito de Pobles del Sud. Proporciona una estimación para dicho precio sabiendo que su porcentaje de vivienda turística es de 0,5. Indica, en porcentaje, la fiabilidad de esta estimación.
- Interpreta los valores de a y b.
(Nota: Este ejercicio se propuso en una prueba del grado de Turismo de la Facultad de Economía de Valencia.)
Ejercicio 3.10 En una planta industrial se ha observado que el número de accidentes laborales podría estar relacionado con el número de horas de trabajo semanales. Se quiere analizar si existe una relación lineal entre estas dos variables. Para ello, durante un mes se ha monitoreado 25 empleados en diferentes turnos. Se registraron las horas de trabajo semanales de cada empleado, tomando en cuenta el control de asistencia de la empresa y se documentaron todos los incidentes reportados en el mismo mes a través del sistema de salud y seguridad ocupacional de la empresa. Cada accidente registrado se relacionó con el empleado afectado. Los datos (simulados) registrados se encuentran disponibles en www.uv.es/ticstat/ejercicio_3_10.xlsx. Realiza los cálculos a mano y verifica los resultados en Excel. Incluye en tu resolución representaciones gráficas comentadas.
Ejercicio 3.11 Para una muestra de 50 empleados de distintos departamentos de una gran multinacional, se ha registrado su edad, en base a los expedientes de RRHH, y el número de lesiones por sobreesfuerzo que figuran en los informes de salud laboral que se presentaron el último año. Se quiere analizar si existe una tendencia en la que los trabajadores de mayor edad sufren más lesiones por sobreesfuerzo. Los datos (simulados) se encuentran disponibles en www.uv.es/ticstat/ejercicio_3_11.xlsx. Realiza los cálculos a mano y verifica los resultados en Excel. Incluye en tu resolución representaciones gráficas comentadas.
Ejercicio 3.12 Una empresa de consultoría y formación desea evaluar si los cursos de capacitación en seguridad laboral tienen un impacto en la reducción de accidentes. Para ello, ha recopilado datos de una muestra de 100 trabajadores del sector de la construcción. En estos datos se incluye el número de cursos de seguridad completados por cada trabajador y el índice de accidentes por cada 100 empleados en las empresas donde trabajan. Los datos (simulados) se encuentran disponibles en www.uv.es/ticstat/ejercicio_3_12.xlsx. Realiza los cálculos a mano y verifica los resultados en Excel. Incluye en tu resolución representaciones gráficas comentadas.
Ejercicio 3.13 La recta de regresión de Y/X de una variable bidimensional (X, Y) es: \[y=3 + \frac{1}{2}\cdot x\] Si además el coeficiente de determinación (bondad de ajuste) es \(R^2=1\) y la varianza de Y es \(S^2_Y= 25\), obtener, comentando los resultados, la varianza residual y la varianza debida a la regresión.
Ejercicio 3.14 A partir de los datos de la Contabilidad Nacional de España, correspondientes al producto interior bruto a precios de mercado (Y) y las exportaciones de bienes y servicios (X), expresados en miles de millones de euros y referidos a cada uno de los 8 años comprendidos en el período 1995-2002, se han obtenido los valores medios, las varianzas y las covarianzas siguientes: \[\overline{y}=556.6 \qquad S^2_Y=8,569.5 \qquad \overline{x}= 152.6 \qquad S^2_X=1,460 \qquad S_{XY}=3,489\] - Obtener una relación lineal que permita explicar el comportamiento del producto interior bruto en función de las exportaciones. Interpretar los coeficientes estimados del modelo. - Si el valor de las exportaciones de bienes y servicios en el año 2003 se estima en 207 mil millones de euros, obtener, razonadamente, una estimación del valor del producto interior bruto en ese año. Valora la fiabilidad de la estimación obtenida. - Sabiendo que en el año 2001 el valor del producto interior bruto fue de 653.9 mil millones de euros, proporciona una estimación de la tasa de variación relativa del producto interior bruto en el período 2001- 2003. Interpreta el resultado obtenido.
Ejercicio 3.15 Una empresa fabrica fibras flexibles a base de mezclar elastómeros con el producto base. La tabla siguiente recoge la elongación del tejido (variable Y) en función de la proporción de elastómero (variable X) añadido por unidad de producto terminado.
| X (% elastómero | Y (elongación, mm) |
|---|---|
| 0 | 4.9 |
| 5 | 10.3 |
| 10 | 21.2 |
| 15 | 22.3 |
| 20 | 20.1 |
| 25 | 27.3 |
Entre otros valores, se han obtenido las siguientes sumas: \[\sum X_i=75 \qquad \sum Y_i=106.1 \qquad \sum (x_i-\overline{x})^2= 437.3 \qquad \sum (y_i-\overline{y})^2=349.9293 \qquad \sum (x_i-\overline{x}) (y_i-\overline{y})=356.25\] - Analiza la correlación lineal entre el% de elastómero y la elongación de la fibra. Interpreta el resultado. - Obtén la recta de regresión de X sobre Y. - Interpreta los valores estimados de los parámetros de la regresión obtenida en el apartado anterior. - Calcula el porcentaje de élastómero que se necesita si deseamos que la elongación sea de 15.2 mm. - Evalua el grado de fiabilidad del valor estimado en el apartado d e interpreta el resultado obtenido.