Què és el mètode japonés de la multiplicació?

El mètode japonés, conegut també com a mètode de les línies, és una forma visual de realitzar multiplicacions que combina matemàtiques amb representacions gràfiques. No es tracta d’un algoritme oficial utilitzat a les escoles del Japó, però sí d’un recurs molt popular en l’àmbit educatiu per la seua capacitat d’ajudar a entendre el concepte de multiplicació d’una manera senzilla i atractiva.

Una de les seues grans virtuts és que no cal conéixer les taules de multiplicació per poder aplicar-lo. Això el fa especialment útil en els primers cursos de Primària, o en contextos de Necessitats Educatives Especials, on és important introduir els conceptes de forma intuïtiva, concreta i visual. En lloc de centrar-se només en nombres i símbols, aquest mètode utilitza línies i interseccions que ajuden l’alumne a veure com interactuen els factors d’una multiplicació.

Procediment pas a pas:

Exemple: 21 × 23

1. Descomposició dels nombres:

Primer, descomponem els dos nombres en desenes i unitats:
21 → 2 desenes i 1 unitat
23 → 2 desenes i 3 unitats

2. Dibuixar les línies:

Dibuixem dues línies paral·leles (pel 2 de les desenes del 21) → deixem un espai → una línia (per la unitat del 21)
A continuació, en perpendicular, dibuixem dues línies (pel 2 de les desenes del 23) → espai → tres línies (per les 3 unitats del 23)

3. Comptar les interseccions segons les diagonals:

Esquerra (intersecció de desenes): 2 × 2 = 4
Centre (barreja de desenes i unitats): (2 × 3) + (1 × 2) = 6 + 2 = 8
Dreta (intersecció d’unitats): 1 × 3 = 3

4. Agrupar els resultats segons la seua posició decimal:

4 → centenes = 400
8 → desenes = 80
3 → unitats = 3

5. Fer la suma final:

400 + 80 + 3 = 483

Per a què serveix a l’aula?

El mètode japonés és una eina molt potent per a l’aprenentatge de la multiplicació perquè va més enllà del càlcul mecànic. Ajuda els alumnes a entendre el significat profund de l’operació, en mostrar com cada xifra d’un nombre interactua amb cada xifra de l’altre. Així, es reforcen conceptes fonamentals com el valor posicional, la descomposició numèrica i el sentit del càlcul.

A més, el seu component gràfic transforma l’operació en una activitat quasi artística, la qual cosa fa que els alumnes gaudisquen de l’experiència i s’impliquen activament. És especialment valuós en aules diverses, on conviuen diferents estils d’aprenentatge, ja que permet que els alumnes visuals, kinestèsics i creatius troben un camí propi cap a la comprensió matemàtica.

⚠️ Quines limitacions té?
Tot i els seus beneficis, cal ser conscients de les seues limitacions. Quan els nombres són molt grans (amb diverses xifres) o inclouen decimals, el sistema es torna poc pràctic i pot resultar confús. El dibuix es complica, les interseccions es multipliquen i és fàcil perdre’s.

També pot passar que els alumnes compten malament les interseccions o que no mantinguen una organització clara del gràfic. Per això, és important introduir-lo de forma guiada, amb exemples senzills, i reforçar sempre la connexió entre el dibuix i el significat matemàtic.

Per què entusiasma als alumnes?
Aquest mètode capta ràpidament l’atenció dels alumnes perquè els permet fer matemàtiques d’una manera nova i creativa. És molt visual i té un component estètic: dibuixar línies, observar com es creuen, descobrir patrons... Tot això transforma una simple multiplicació en un repte divertit.

També desenvolupa habilitats importants com l’atenció al detall, l’ordre i la coordinació visuo-motriu. Cal seguir una seqüència concreta, fixar-se en les diagonals, comptar bé... I això genera un hàbit de treball metòdic que pot ser molt beneficiós. A més, el fet que es puga repetir fàcilment anima a l’autocorrecció i fomenta la perseverança i la confiança.

Propostes per treballar-lo a l’aula
Hi ha moltes maneres de fer aquest mètode encara més atractiu i significatiu:

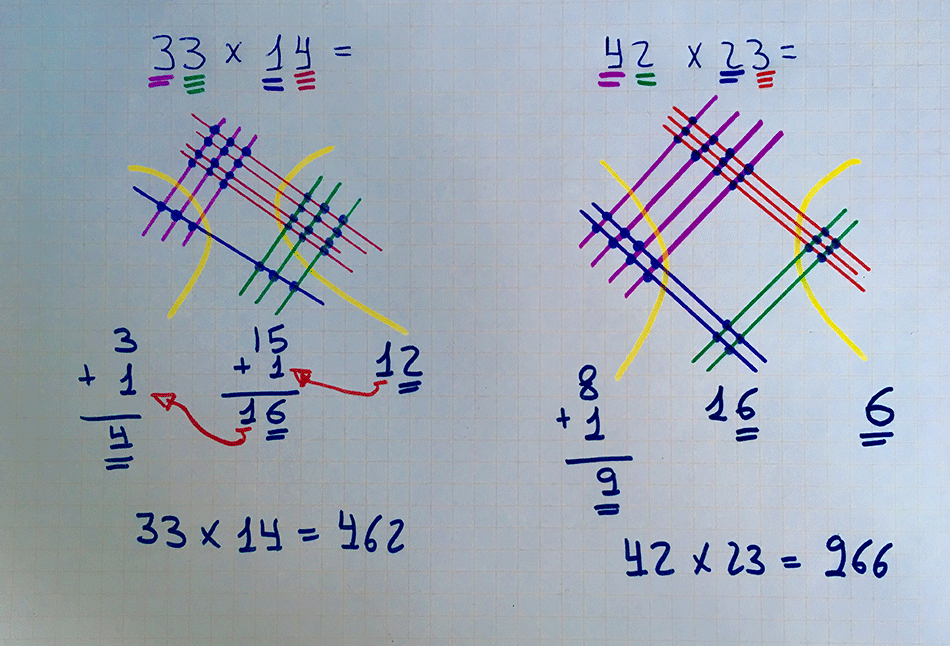
1. Amb retoladors de colors: Assignar un color per a cada valor posicional (desenes i unitats) ajuda a distingir les línies i a evitar errors.
2. En treball cooperatiu: Un alumne pot encarregar-se de fer el dibuix i un altre de comptar i sumar les interseccions. Això afavoreix el diàleg i la col·laboració.
3. Mitjançant la formulació d’hipòtesis: Es poden plantejar preguntes com “Què passaria si en lloc de dues línies en férem tres?” o “Com canviaria el resultat si canviem l’ordre dels factors?”
4. Amb reptes visuals: Per exemple, donar als alumnes un dibuix fet i demanar-los que troben quins nombres s’estan multiplicant.
5. Creant murals col·lectius: Amb cartolines grans, l’alumnat pot representar multiplicacions com a obra d’art, decorant l’aula amb matemàtiques visuals.