Els antics egipcis, tot i no tindre un sistema numèric posicional ni conéixer les taules de multiplicació tal com les entenem hui, van desenvolupar un sistema molt enginyós per realitzar càlculs. Aquest mètode, basat en la duplicació i la descomposició binària, permetia multiplicar dos nombres de manera segura i eficaç utilitzant només sumes i duplicacions, és a dir, operacions senzilles però molt potents.

La clau està en representar un dels factors com a suma de potències de dos (com fan els ordinadors en el sistema binari), i després seleccionar les corresponents duplicacions de l’altre factor. És una estratègia amb una gran base lògica que mostra com, fa milers d’anys, les persones ja sabien aplicar el raonament matemàtic de manera pràctica i sistemàtica.

🧮 Procediment pas a pas:
Exemple: 25 × 18

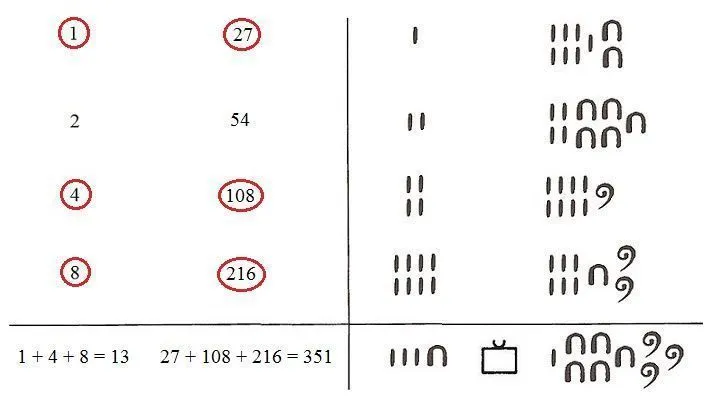
1. Crear dues columnes:
Col·loquem els valors en dues columnes:

A l’esquerra: comencem amb 1 i anem duplicant fins superar el primer factor (25)
A la dreta: partim de l’altre factor (18) i dupliquem cada vegada també

2. Descompondre 25 com a suma de potències de 2:
25 = 16 + 8 + 1
3. Seleccionar les files que corresponguen a aqueixos valors:
Quedem-nos amb les files on l’esquerra siga 16, 8 i 1
4. Sumar els valors corresponents de la columna de la dreta:
288 (de 16) + 144 (de 8) + 18 (de 1) = 450

Què ensenya aquest mètode?

Aquest sistema no només ensenya a multiplicar. Ens obri la porta a una forma de pensar més analítica i estructurada, que implica:

Aprendre a descompondre un nombre en parts útils per al càlcul. Això reforça la idea de la descomposició numèrica, tan important en el pensament matemàtic.
Entendre com les duplicacions poden construir qualsevol quantitat, de manera semblant a com funciona el sistema binari.
Desenvolupar la lògica i la capacitat d’observació, ja que cal identificar correctament quines files són rellevants i quines no.
Potenciar la capacitat d'autocorrecció, ja que si el resultat final no és correcte, es pot revisar fàcilment pas a pas.

Aplicació didàctica: una finestra al passat (i al futur)

Aquest mètode és una oportunitat excel·lent per mostrar a l’alumnat que les matemàtiques tenen història i que han evolucionat amb les civilitzacions. Pot generar converses molt interessants sobre com les societats del passat resolien problemes quotidians i com el coneixement s’ha anat transmetent i refinant.

Al mateix temps, connecta amb el pensament computacional, ja que el sistema binari és la base de tot el món digital. És una forma fantàstica d’introduir nocions de codi binari, estructures lògiques i fins i tot de programació primitiva.

🧠 Reptes cognitius que fomenta

1. Descomposició numèrica complexa: No sempre és fàcil veure que, per exemple, 27 = 16 + 8 + 2 + 1. Aquests exercicis ajuden a entrenar la ment en la recerca d’estratègies.
2. Raonament lògic: Els alumnes han de deduir quines files triar segons la descomposició, la qual cosa suposa una activació constant del pensament crític.
3. Seguretat i autocorrecció: Si el resultat final no quadra, l’alumne pot revisar els passos i identificar l’error amb facilitat. Això reforça la metacognició i l’autonomia en l’aprenentatge.

Estratègies per aplicar-lo a l’aula

Per convertir aquest mètode en una experiència significativa, es poden utilitzar propostes creatives com:

1. Representació manipulativa: Crear taules de duplicació amb fitxes, pedres o caixetes que s’han d’anar duplicant i sumant segons el cas. Ideal per a treballar amb nens i nenes més visuals o kinestèsics.
2. Activitat d'inversió lògica: Plantejar reptes com “El faraó ha fet una multiplicació secreta i ha obtingut 234. Quines files ha utilitzat?” Així es treballa la descomposició a l’inrevés.
3. Teatralització històrica: Simular una escena de l’Antic Egipte, amb disfresses i ambientació, on els alumnes fan de matemàtics reials i han de resoldre multiplicacions per ajudar al faraó.
4. Gamificació: Fer una cursa de càlcul per veure qui troba més ràpidament la descomposició correcta i el resultat.
5. Relacionar-lo amb la informàtica: Mostrar com aquest sistema antic s’assembla al que fan els ordinadors quan treballen amb codi binari, ajudant a establir ponts interdisciplinaris.