Moltes vegades tendim a usar mètodes de resolució típics de la resolució directa quan realment les magnituds que usem no tenen cap relació d’aquest tipus:
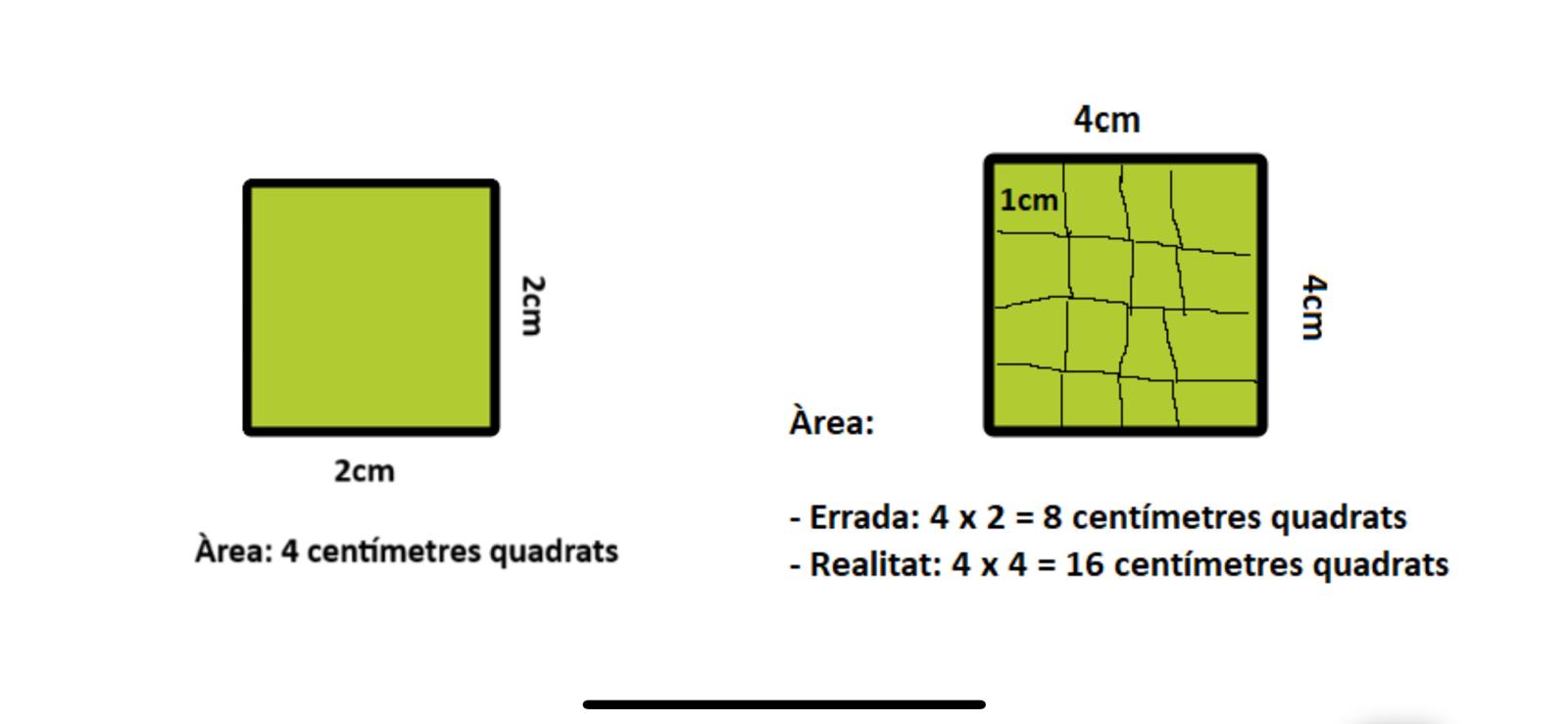
Per exemple: si un quadrat de 2cm de costat té una àrea de 4cm quadrats, un de 4cm de costat tindrà 8cm quadrats.
Per exemple: si amb un treballador venem 100 gelats al dia, amb cinc en vendrem 500.
Aquesta tendència errònia de la realitat afecta a problemes de volum, àrea i altres. L’alumnat tendeix a aplicar les relacions proporcionals a problemes on clarament no té sentit aplicar-les, com veiem en l’article de Sánchez & Juárez, 2017. Aquest error clàssic es deu a la simplicitat de les relacions lineals, que provoquen la seua generalització a situacions no lineals.
HEM D’ANALITZAR LES RELACIONS DE PROPORCIONALITAT PER ASSEGURAR-NOS DE QUE DOS MAGNITUDS SÓN DIRECTAMENT PROPORCIONALS:
Per a que dues quantitats siguen directament proporcionals, la seua raó, o quocient entre elles, ha de ser sempre el mateix, encara que varien les quantitats. En altres paraules, les magnituds A i B han d’augmentar o disminuir de la mateixa manera.
Expressat en llenguatge matemàtic:
A1/B1 = A2/B2 = A3/B3 = An/Bn
El resultat d’aquesta fracció s’anomena constant de proporcionalitat (k).
Per exemple: si 3 kilos de peres val 1.8 €
3/1.8 = 5/3 = 8/4.8 = 1.666…
És per això que hem d’analitzar detalladament la relació entre magnituds per certificar es tracta d’una relació de proporció directa o d’un altre tipus de relació.