Les operacions de conjunts permeten combinar o comparar conjunts per a identificar les relacions entre els seus elements, com a unió, intersecció, diferència i complement. Són essencials per a l'anàlisi lògica i matemàtic.
UNIÓ DE CONJUNTS
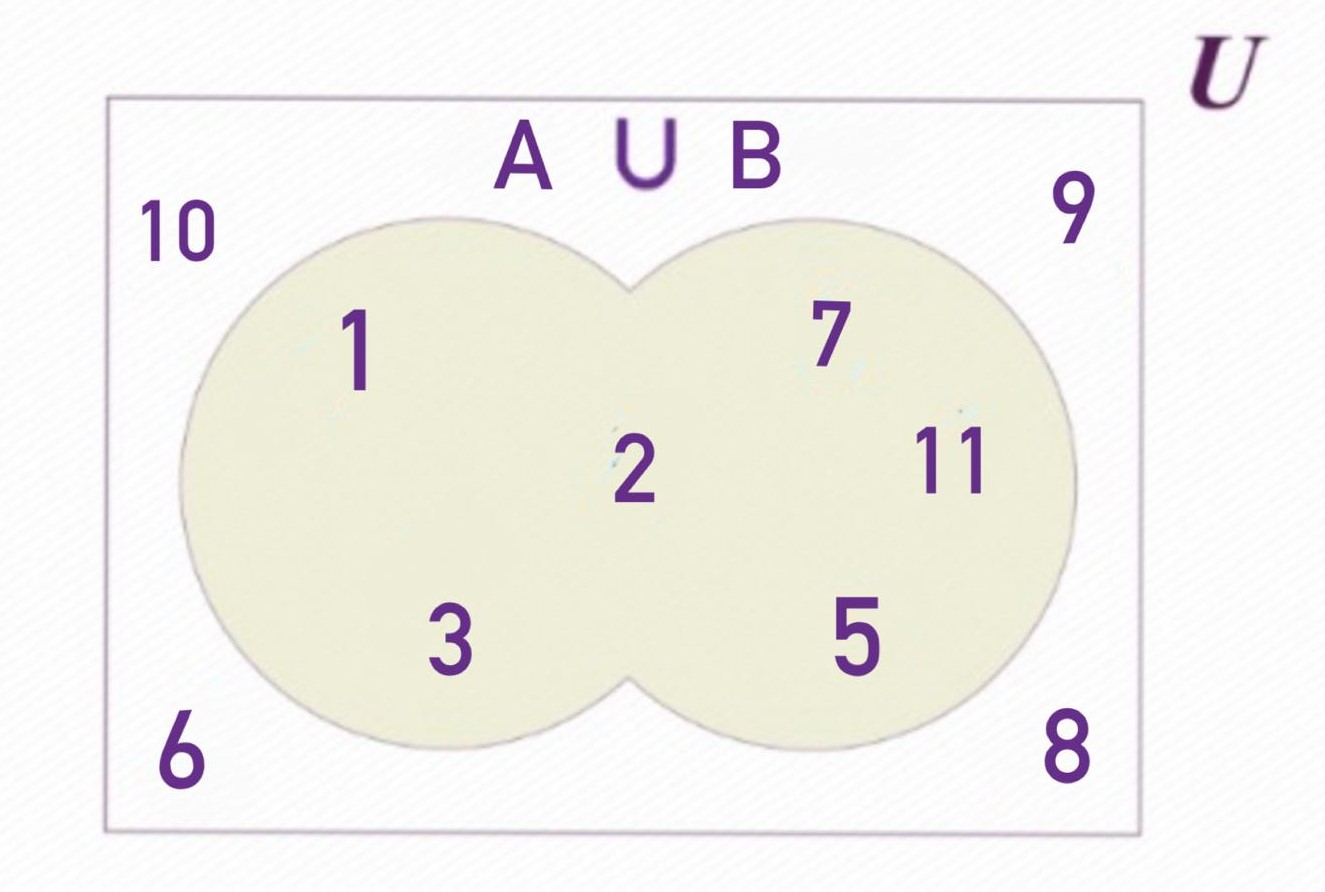
La unió de conjunts es referix a la combinació d'elements que pertanyen a dos conjunts, A i B. En altres paraules, és un conjunt format per tots els elements que estan en A, en B o en els dos. Este nou conjunt es denota com A ∪ B.
Per a determinar quins elements formen part de la unió, simplement has d'identificar els que estan en A "o" en B. En aquest cas, el conjunt resultant inclou tots els elements del conjunt universal que complisquen amb esta condició.
Per exemple, si tenim els conjunts A i B, la unió A ∪ B quedaria conformada de la manera següent: A ∪ B = {1, 2, 3, 5, 7, 11}.
INTERSECCIÓ DE CONJUNTS
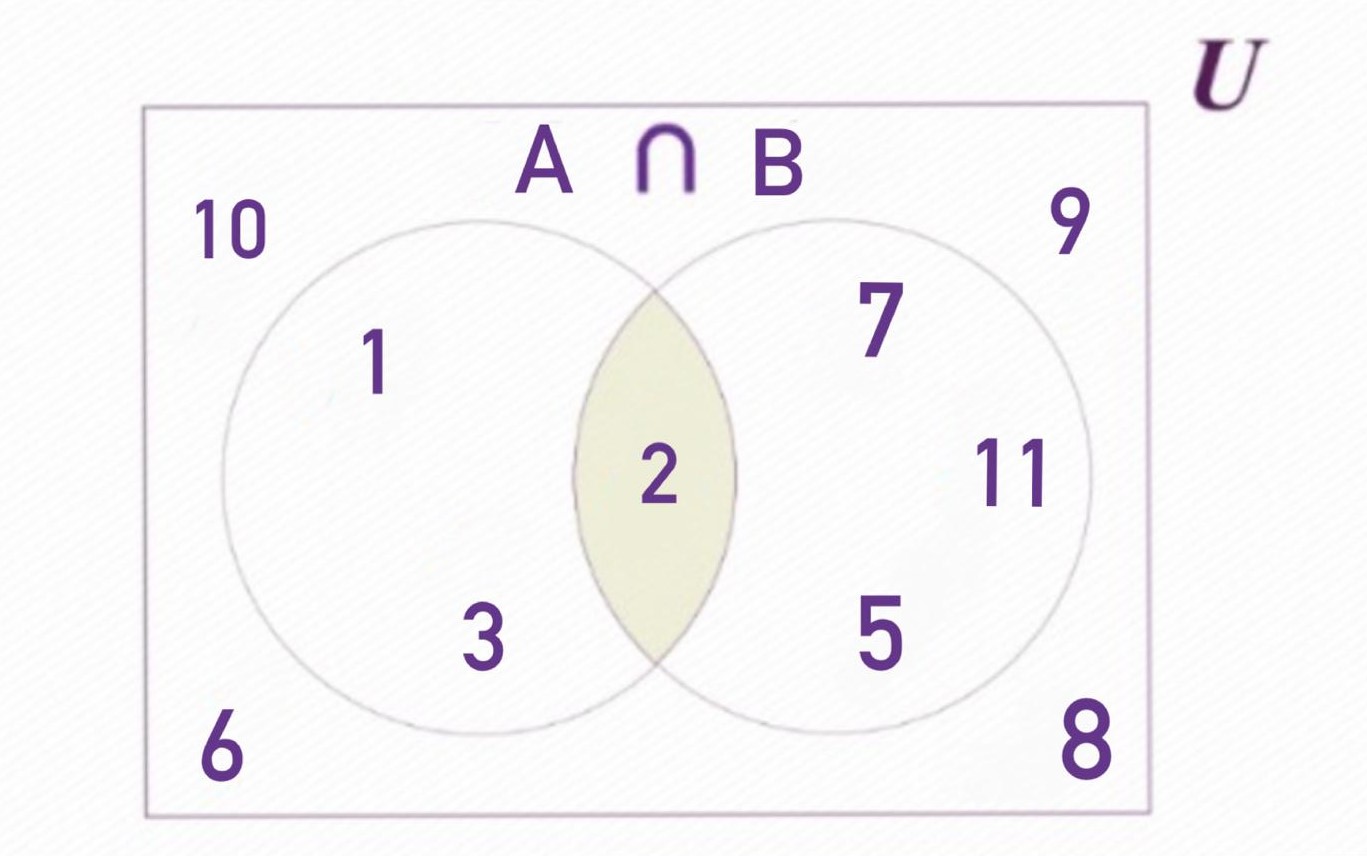
La intersecció de conjunts es referix als elements que dos conjunts, A i B, tenen en comú. És a dir, es forma un nou conjunt compost exclusivament pels elements que estan tant en A com en B. Aquest conjunt es denota com A ∩ B.
Per a identificar quins elements pertanyen a la intersecció, n'hi ha prou amb preguntar-te quins són presents en A "i" en B al mateix temps. El conjunt resultant inclourà únicament aquells elements del conjunt universal que complisquen amb esta condició.
En l'exemple esmentat, la intersecció dels conjunts A i B queda de la manera següent: A ∩ B = {2}.
DIFERÈNCIA DE CONJUNTS
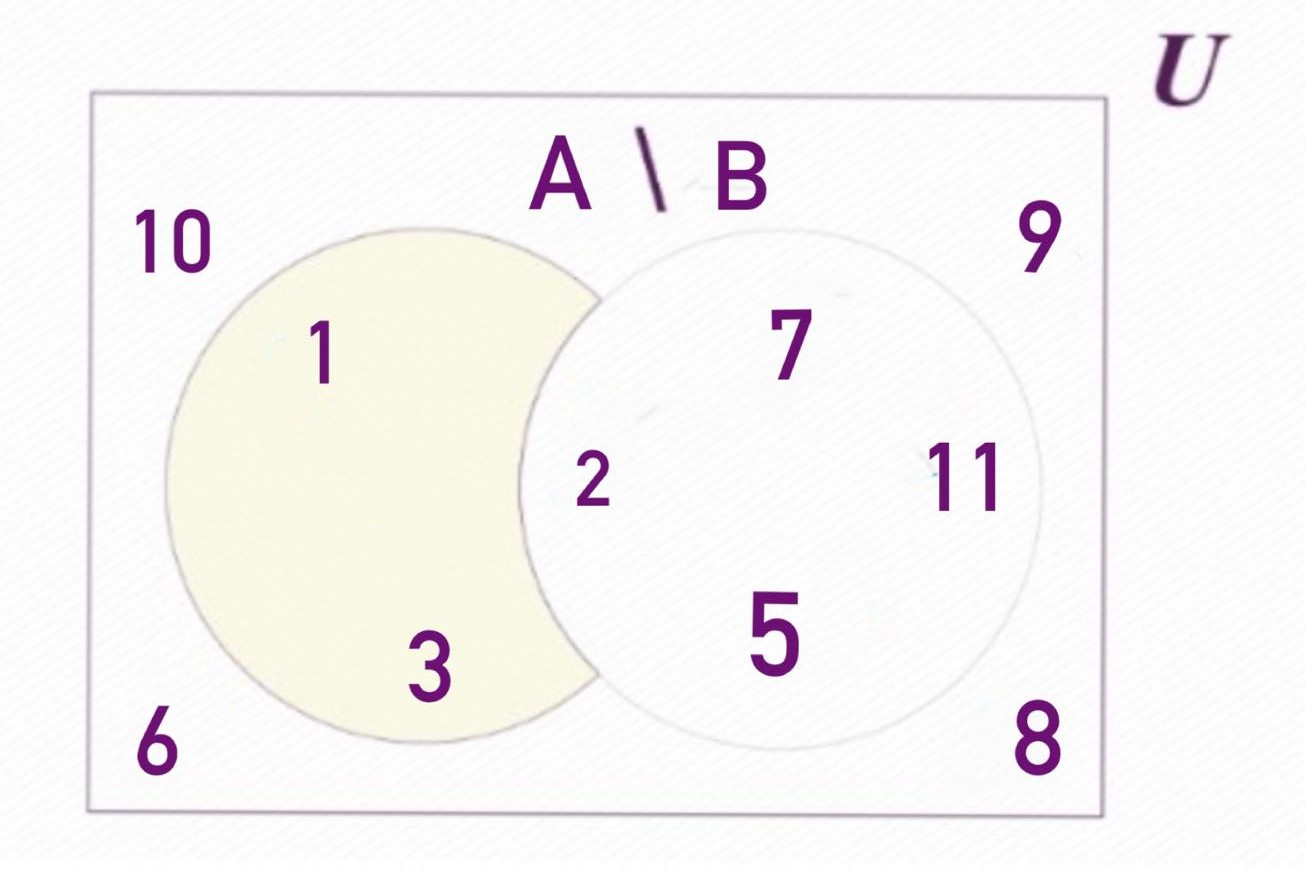
La diferència de conjunts és una operació que consisteix a identificar els elements d'un conjunt que no són presents en un altre conjunt. Per exemple, si realitzem l'operació A menys B (denotada com A \ B), seleccionem exclusivament aquells elements que pertanyen al conjunt A però que no es troben en el conjunt B.
En aquest cas, el resultat de la diferència entre els conjunts A i B és: A \ B = {1, 3}.
DIFERÈNCIA SIMÈTRICA DE CONJUNTS
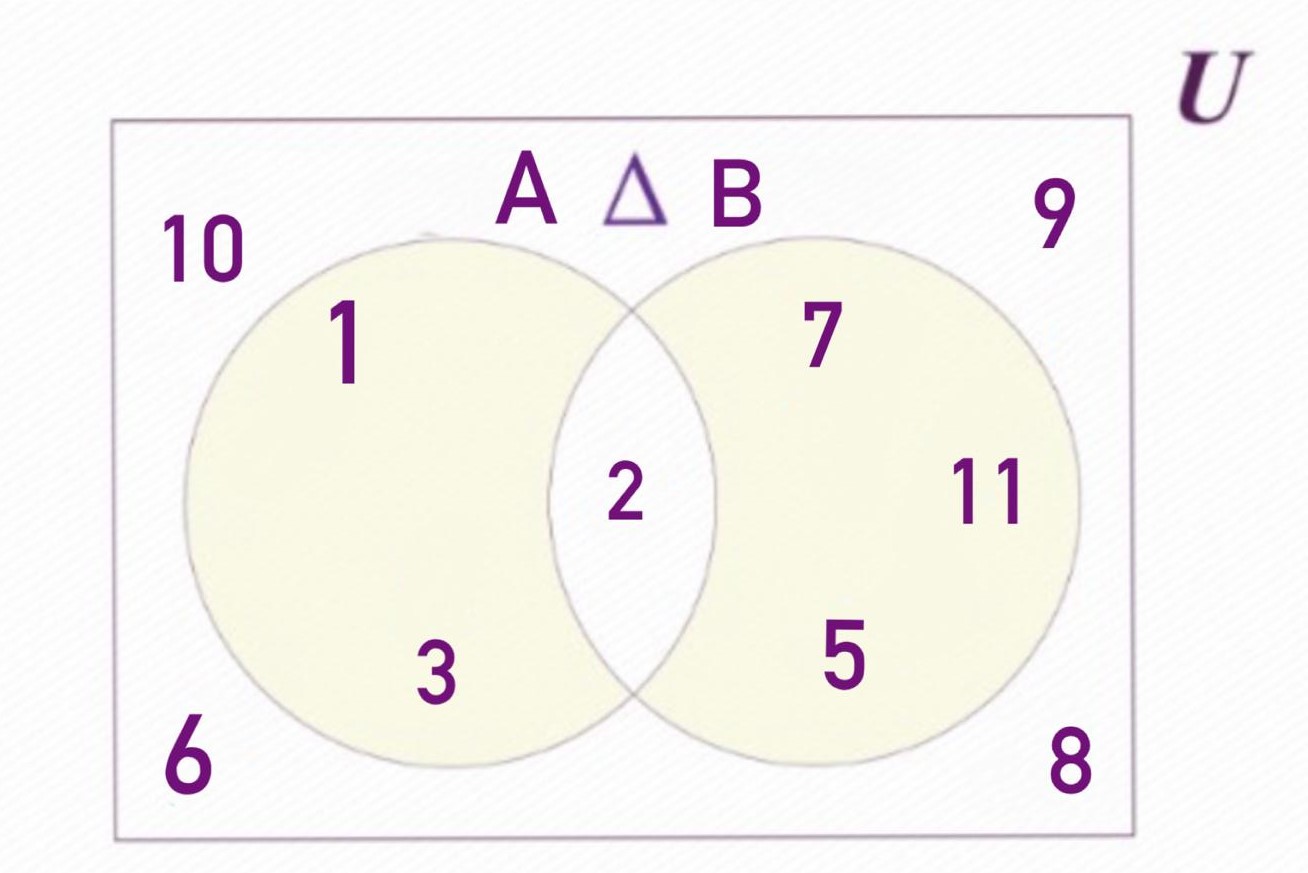
La diferència simètrica de conjunts és una operació que identifica els elements únics de dos conjunts, és a dir, aquells que pertanyen a un o a l'altre, però no als dos simultàniament. Això significa que s'inclouen els elements d'A fet que no estan en B i els elements de B que no estan en A. Es denota mitjançant el símbol Δ.
En el cas dels conjunts A i B, el resultat de la diferència simètrica seria: A Δ B = {1, 3, 5, 7, 11}.
COMPLEMENT D'UN CONJUNT
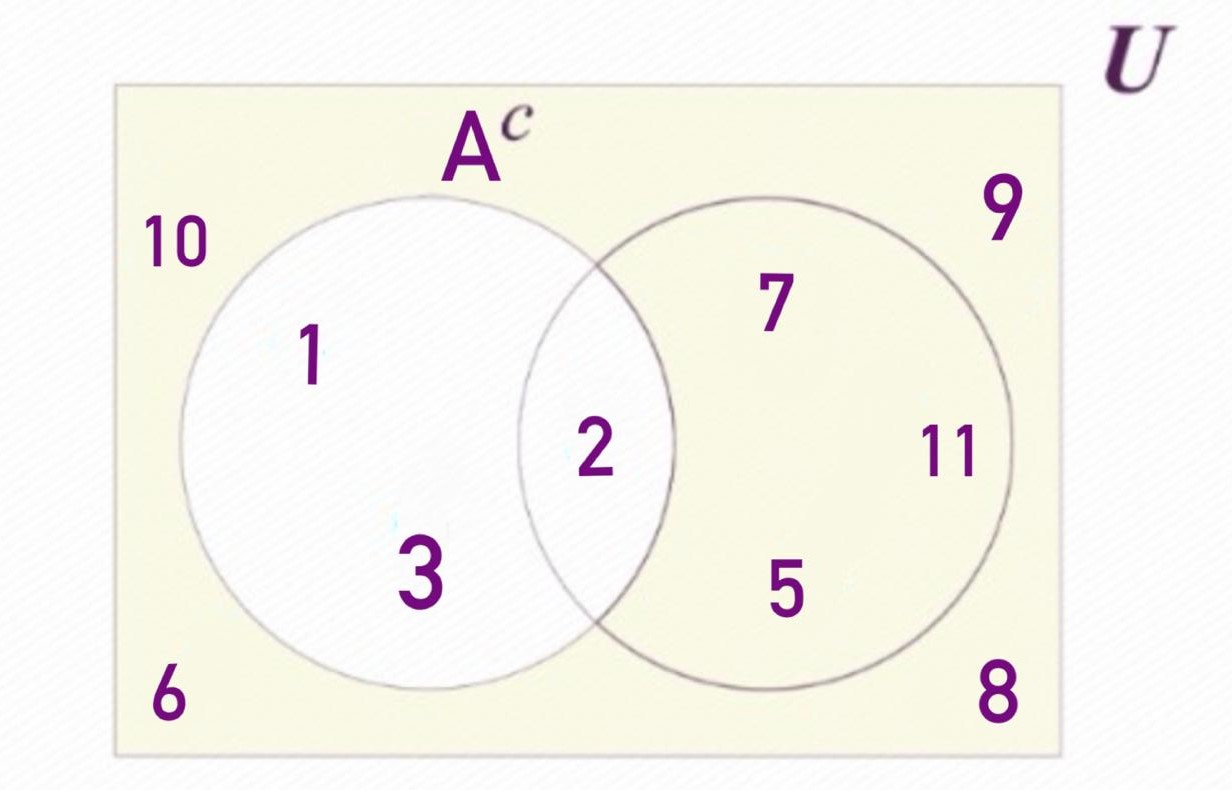
El complement d'un conjunt és una operació que consisteix a identificar tots els elements del conjunt universal U que no estan en el conjunt A. En altres paraules, és el conjunt format per aquells elements que no pertanyen a A. Aquesta operació no compara dos conjunts, sinó que es relaciona únicament amb un conjunt i el conjunt universal.
El complement d'A se denota comunament com 
, i per al conjunt B, el seu complement es representaria com a 
.
En l'exemple proporcionat, el complement dels conjunts seria: = {10, 6, 7, 5, 11, 9, 8} = {9, 8, 10, 6, 1, 3}
En la Teoria de Conjunts, existeixen lleis similars a les de l'aritmètica que regixen com es realitzen les operacions entre conjunts. Entre elles estan:
Llei commutativa: El resultat de la unió o intersecció de dos conjunts no depén de l'orde en què es realitze l'operació. Per exemple:
A ∪ B = B ∪ A
A ∩ B = B ∩ A
Llei associativa: Quan realitzem la unió o intersecció de tres conjunts, el resultat no varia depenent de com s'agrupen els conjunts:
A ∪ (B ∪ C) = (A ∪ B) ∪ C = A ∪ B ∪ C
A ∩ (B ∩ C) = (A ∩ B) ∩ C = A ∩ B ∩ C
Llei distributiva: Esta llei descriu com estendre una operació d'unió o intersecció cap a l'interior d'una altra operació:
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)