3.2 Minimización del error de predicción

Minimizar el error de predicción significa obtener los coeficientes de la recta de Regresión con los que la suma de cuadrados de errores de predicción es la menor posible. Sea el siguiente ejemplo:

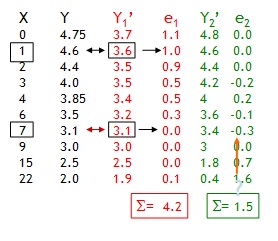
La suma de cuadrados de errores es más pequeña con la segunda ecuación que con la primera, y por tanto diremos que la segunda ecuación es preferible. Podríamos definir arbitrariamente más ecuaciones y calcular el error de predicción, pero interesa saber cuál es la ecuación que da el menor error de predicción.

Los valores de los coeficientes a y b que definen la mejor ecuación según el criterio de mínimos cuadrados son obtenidos con las siguientes fórmulas:

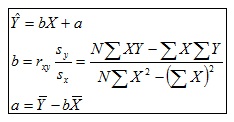
Con los datos del ejemplo, la mejor ecuación según el criterio de mínimos cuadrados es:

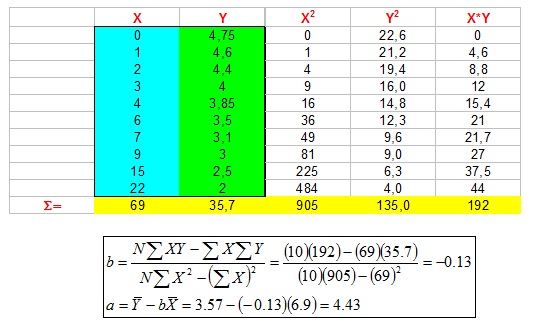
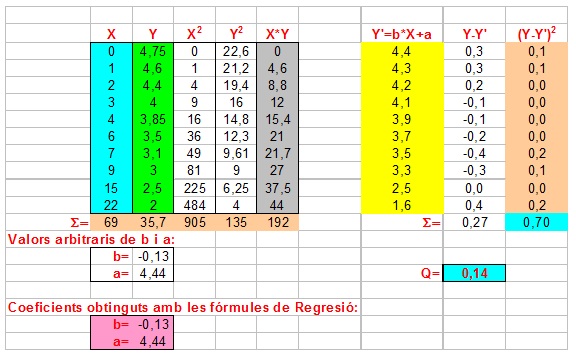
El sumatorio (suma) de cuadrados de los errores con esta ecuación es igual a 0.14, más pequeño que los sumatorios de cuadrados obtenidos con las otras ecuaciones.

(Clicando de forma repetida puedes activar la siguiente hoja de cálculo si tu ordenador dispone de Excel. Prueba a introducir otros valores a los coeficientes b y a y observa cómo cambian: Las predicciones, los errores de las predicciones y el valor del coeficiente Q. Haz la comparación con los resultados obtenidos con los coeficientes dados por las fórmulas de Regresión).