Considereu l'exemple següent: un psicòleg fa el seguiment d'un estudiant de Batxillerat i troba que en els exàmens de Matemàtiques (M) i en el d'Història (H) ha obtingut un 5. Les puntuacions obtingudes pels estudiants dels dos grups són:

En relació amb els resultats obtinguts per la resta de membres del grup, l'estudiant ha quedat molt bé en Matemàtiques i malament en Història. Des del punt de vista dels procediments d'anàlisi de dades, la conclusió és que les puntuacions directes NO informen d'una manera adequada de la posició de la puntuació en relació amb la resta de puntuacions del grup. Per tant, cal disposar d'un procediment que ho faça.

Si en compte d'operar en les puntuacions directes obtenim el percentatge de puntuacions amb valors inferiors, resulta que l'estudiant ha obtingut una puntuació en Matemàtiques que deixa per baix el 80% de les puntuacions i en Història, el 10%. Està clar que així sí que podem comparar el rendiment de l'estudiant en els dos exàmens: el rang percentil d'una puntuació x es defineix com el percentatge de dades amb valors inferiors a x.

Càlcul

Fórmula de càlcul:

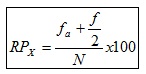
f_a: freqüència acumulada fins al límit inferior de l'interval on es troba la puntuació x.

f: freqüència de la puntuació x.

 

Exemple

Obtenció del rang percentil de la puntuació 6:

.

En conseqüència, direm que per baix de la puntuació 6.0 trobem el 40% de les puntuacions.

(Assumim que les quatre puntuacions amb valor 6 es distribueixen de manera uniforme al llarg de l'interval 5.5-6.5.)