Amplitud

L'amplitud total (A_T) és la diferencia entre la puntuació de major valor i la de menor valor:

L'amplitud total és un estadístic molt senzill i fàcil de calcular, però sovint ésta simplicitat és un inconvenient. Consideréu el següent exemple:

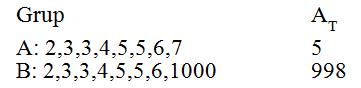
Els grups A i B són bastant semblants, però els coeficients d'amplitud no. La diferència en els coeficients és ocasionada per la variació introduïda per una sola puntuació amb valor extrem, el 1000. Per esta raó sembla convenient disposar d'altres mesures més adequades.

Característiques principals: el coeficient d'amplitud total no té en compte els valors entre extrems, que son els únics que en determinen el valor de manera directa .

 

Variància i desviació típica

La variància i la desviació típica compten en totes les puntuacións, i son definides per les expressions següents:

Motivació:

Considerem les dades següents:

La diferència de cada puntuació respecte de la mitjana (que és de 5 en els tres grups) dóna:

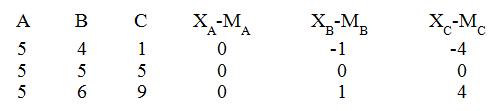
Com més gran és la magnitud de les diferencies entre les dades, més gráns son els valors de les diferències respecte de la mitjana. Una forma senzilla de resumir la informació en cadascuna de les columnes de diferències consisteix a sumar-les. Però tenim un problema: les sumes de diferències respecte de la mitjana sempre són 0, per la qual cosa no informen de les diferències entre les dades.

Per a resoldre elproblema, elevem al quadrat cadascuna de les diferències i les sumem:

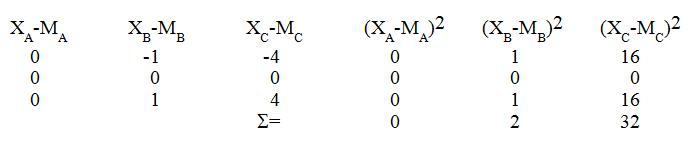
La suma de quadrats de diferències al grup A, on no hi hà variació, és 0, la del grup B, on hi hà variació de baixa magnitud, és 2, i la del grup C, on la variació és de major magnitud que al grup B, la suma prèn major valor: la suma de quadrats és un estadístic sensible a la variació entre totes les dades del grup. Si dividim per N per tal de fer possible la comparació entre grups de diferents grandàries tenim la variáncia:

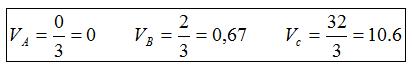
Podeu comprovar que la variància dóna 0 en el grup A, on no hi hà variació, i pren valors positius de magnitud més gran quantes més i de major magnitud son les diferències entre les dades dins de cada grup.

La variància mesura la variació a partir dels quadrats de les diferències, la qual cosa tè com a conseqüència que està expressada en una escala de quadrats. Per a obtenir una mesura en la mateixa escala de la variable, afegim l'arrel quadrada a l'expressió de la variància, i resulta la desviació típica:

 

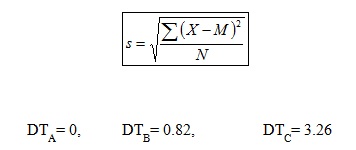
Quasivariància

La quasivariància és:

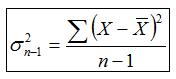
És semblant a la variància, llevat que la divisió es per n-1 (grandària de la mostra) i no per N (grandària del grup de dades). La quasivariància és adequada per obtenir estimacions de la variància de la població en l'análisi inferencial de dades.

Característiques principals

Variància: NO se expresa en l'escala original de la variable.

Desviació típica: molt sensible a les punctuacions extremes.

Variància i desviació típica:

a) Tenen com a valor mínimo el 0, y no tenen máxim.

b) No alteran el seu valor si afegim una constant a las punctuacions: