Són dades que no consten degut a qualsevol esdeveniment, com ara errades a la transcripció de les dades o l'absència de disposició a respondre a certes qüestions d'una enquesta. Les dades poden faltar de manera aleatòria o no aleatòria.

Les dades faltants aleatòries poden pertorbar l'anàlisi de dades donat que disminueixen la grandària de les mostres i en conseqüència la potència a les proves de contrast d'hipòtesis. Les dades faltants no aleatòries ocasionen, a més, disminució de la representativitat de la mostra.

Tractament

De casos complets o eliminació per llista.

Este procediment consisteix a incloure a l'anàlisi els casos que presenten observacions completes en totes les variables. Este mètode sols ha d'utilitzar-se quan el procés d'arreplegada de dades és aleatòri, perquè en un altre cas introduïeix biaix. Un altre inconvenient és que la grandària mostral pot arribar a patir una gràn reducció i afectar a la representativitat de la mostra.

Selecció per variables

Es mantenen els casos que tenen dades en les variables requerides per els càlculs a que estém interessats. Este procedimen té l'inconvenient de generar mostres heterogénies.

Mètodes d'imputació

Els mètodes d'imputació consisteixen en estimar els valors absents en base als valors vàlids d'altres variables i/o casos de la mostra. La estimació es pot fer a partir de la informació del conjunt complet de variables o bé de no més algunes variables seleccionades. Usualment els mètodes d'imputació s'utilitzen amb variables mètriques (d'interval o de raó), i han d'aplicar-se amb gran precaució perquè poden introduir relacions inexistents en les dades reales.

Principals procediments:

- Sustitució per la Mitjana. Sustituim el valor absent per la Mitjana dels valors vàlids. Este procediment planteja inconvenients com ara:

Dificulta l'estimació de la Variància.

Distorsiona la vertadera distribució de la variable,

Distorsiona la correlació entre variables donat que afegeix valors constants.

- Sustitució per constant. Sustituïm els valors absents per constants el valor dels quals ve determinat per raons teòriques o relacionades amb la investigació prèvia. Presenta els mateixos inconvenients que la sustitució per la Mitjana, i només ha de ser utilitzat si hi ha raons per a suposar que és més adequat que el mètode de la mitjana.

- Imputació per regressió. Este métode consisteix a estimar els valors absents en base a la seua relació amb altres variables.

Inconvenients:

- Incrementa artificialment les relacions entre variables.

- Fà que se subestime la Variància de les distribucions.

- Assumeix que les variables amb dades absents tenen relació d'alta magnitud amb les altres variables.

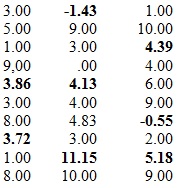
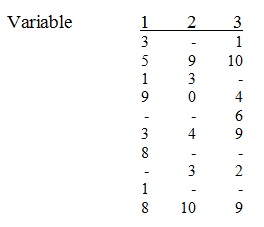
Exemples: El següent conjunt de dades consta de tres variables i deu casos. El conjunt és incomplet perquè a la variable 1 falten les dades dels casos cinq i vuit. A la variable 2 falten les dades dels casos ún, cinq, set i nou. A la variable 3 falten les dades dels casos tres, set i nou.

Estadístics descriptius (Mitjanes) obtinguts excloent els casos incomplets (selecció per llista):

Observeu que la mostra original ha quedat reduïda a quatre casos.

Casos exclosos per variables (per parelles):

A la tabla de l'esquerra pots veure el nombre de parelles amb dades a totes les variables. Per exemple, el nombre de parelles completes de les variables 1 i 2 son cinq, etc.

A la tabla de la dreta apareixen les Mitjanes de cada variable obtingudes incloent els casos amb dades completes en les parelles. Com a exemple, la Mitjana de la variable 1 obtinguda en les dades de la variable 1 que tenen parella en la variable 2 es 5.2

Sustitució per imputació de la Mitjana:

Els valors absents han estat sustituïts per les Mitjanes de les respectives variables:

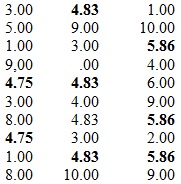
Imputació per Regressió

Els valors absents han estat substituïts per valors estimats mitjançant Anàlisis de Regressió: