Les distribucions de freqüències son el conjunt de modalitats de les variables acompanyades del nombre d'ocurrències per cada modalitat (les freqüències). La finalitat de les agrupacions en freqüències és facilitar l'obtenció de la informació que contenen les dades.

Exemple: volen conéixer si un grup d'individus està a favor o en contra de la exhibició de continguts violents a la televisió, per la qual cosa han arreplegat les següents dades:

X: 2,1,5,3,3,2,3,1,4,2,4,2,3,2,3,4,3,3,1,2

(Regla de codificació:

1= En contra

2= Bastant en contra

3= Indiferent

4= Bastant a favor

5= A favor)

La inspecció de les dades originals no permet donar resposta fàcilment a qüestions senzilles com quína és l'actitud majoritària del grup, i resulta pràcticament impossible respondre a altres qüestions com la magnitud de la diferència d'actitud entre homes i dones.

És podem fer millor idea si disposem una tabla en els valors de la variable acompanyats del nombre de vegades (la freqüència) que apareix cada valor:

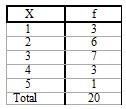
X: Símbol genèric de la variable.

f: Frequència (també es simbolitza com n_i).

La distribució de freqüències de les dades de l'exemple mostra que l'actitud majoritaria dels individus del grup estudiat és indiferent.

La interpretació de les dades ha estat facilitada perquè hem reduït el nombre de números a examinar (per compte de 20, ara tenim 5 valors de la variable i 5 freqüències).

Generalment les tables inclouen varies columnes amb les freqüències relatives (son el nombre d'ocurréncies dividit per el total de dades, i es símbolitzen "f_r" o "p_i"), freqüències acumulades (la freqüéncia acumulada es el total de freqüències dels valors iguals o inferiors al de referéncia, i es simbolitzen "f_a" o "n_a"), freqüències acumulades relatives (la freqüéncia acumulada relativa es el total de freqüències relatives dels valors iguals o inferiors al de referéncia, i es simbolitzen "f_ra" o "p_a")

Exemple:

Considerem el següent grup de dades :

18,35,22,41,35,68,30,30,30,46,42,32,30,16,28,35,35,35,44,44,44,39,44,61,55,32,32,28,28,29,25,25,28,54,53,35,60,35,35,35,64,35,35,34,22,44,17,16,46,46,27,25,46,47,46,35,39,59,59,32,32,28,35,27,31,30,32,61,35,54,57,35,56,44,58,41,42,44,30,40,46,46,50,49,50,36,41,29.

La distribució de freqüències és:

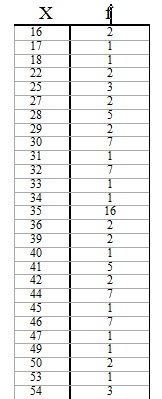
La reducció de dades mitjançant l'agrupament en freqüències no facilita la seua interpretació: la tabla és massa gran. Per tal de reduir la grandària de la tabla agrupem els valors en intervals, i les freqüències son les dels conjunts de valors inclosos en els intervals:

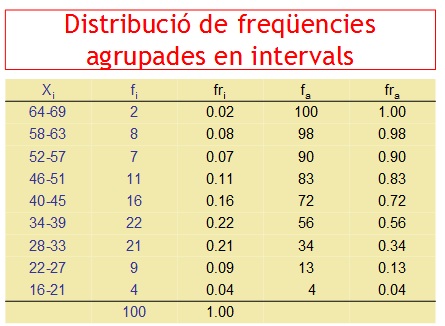
Ara és mes senzill interpretar les dades i, per exemple, podem apreciar d'un cop d'ull que l'interval amb major nombre de dades es el 34-39, o que el 75% de les dades té valor inferior a 46.

Elements bàsics de les tables d'intervals:

• Interval: cadascun dels grups de valors de la variable que ocupen una fila en una distribució de freqüències
• Límits aparents: valor major i menor que son observats a la tabla. Depènen de la precisió de l'instrument de mesura. A l'exemple, els límits aparents de l'interval amb major nombre de freqüències son 34 o 39.
• Límits exactes: valors màxim i mínim de l'interval, que podrien mesurar-se si es comptara amb un instrument de precisió perfecta. A l' interval 34-39, estos límits son 33,5 i 39,5.
• Punt mig de l'interval (M_c o Marca de classe): suma dels límits dividit per dos. Mc de l'interval de l'exemple= 36,5.
• Amplitud de l'interval: diferència entre el límit exacte superior i el límit exacte inferior. A l'exemple es igual a 6.