a) Supuestos:

Además de los supuestos de normalidad e independencia, un supuesto específico para esta prueba es que las Varianzas de los dos grupos sean semejantes.

b) Hipótesis:

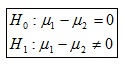
o también

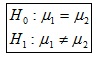
c) Estadístico de contraste:

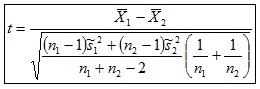
d) Distribución del estadístico de contraste: t con n₁+ n₂-2 grados de libertad.

e) Significación del estadístico de contraste.

g) Intervalo de confianza:

 

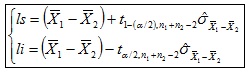
Ejemplo

Dicen que los estudiantes de los grupos de tarde son diferentes a los de los grupos de la mañana. Para comprobarlo han calculado las Medias de los exámenes a los dos grupos. Comprobar esta hipótesis (a= 0.05, datos ficticios)

a) Supuestos: Las muestras han sido obtenidas aleatoriamente, por lo que se asume que los datos son independientes.

b) Hipótesis.

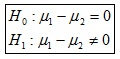
c) Estadístico de contraste:

d) Distribución del estadístico de contraste: t con 110+90-2=198 grados de libertad.

e) Significación del estadístico de contraste: 0.01

f) La significación del estadístico de contraste es inferior a 0.05, por lo que se rechaza la Hipótesis Nula.

g) Intervalo de confianza:

La diferencia entre las medias poblacionales se sitúa entre 0.13 y 0.87 con un nivel de confianza del 95%.

Conclusión: Los datos respaldan la Hipótesis de que los estudiantes del grupo de la tarde difieren de los estudiantes en los otros grupos.