3.1 U de Mann
Es una
alternativa a la prueba t para dos muestras independientes. La prueba se basa en la relación entre las sumas de rangos y las diferencias entre grupos, como puede apreciarse en los siguientes ejemplos:
Los siguientes datos son puntuaciones de sensación de bienestar obtenidas en dos muestras diferentes:
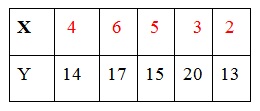
Ordenamos los datos como si fueran una sola muestra y les
asignamos rangos:

Los rangos de los dos grupos están separados, dado que las puntuaciones de los dos grupos son diferentes.
Las sumas de los rangos por filas son:
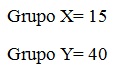
En cambio, consideremos el siguiente ejemplo, donde no hay diferencia entre los grupos comparados:
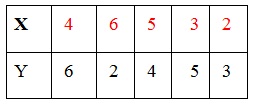
Ordenación de los datos como si fueran de una sola muestra:

Sustituyendo los valores originales por los rangos:
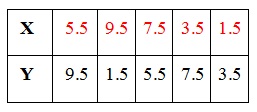
Los rangos de los dos grupos están mezclados, dado que las puntuaciones son parecidas en ambos grupos.
Las sumas de rangos por filas son:
Las sumas dan la misma cantidad porque los rangos asignados a las puntuaciones de los dos grupos son idénticos.
a) Supuestos:
Los datos deben estar medidos a nivel ordinal, cuando menos.
No hace falta suponer normalidad de las distribuciones ni homogeneidad de las Varianzas.
El procedimiento se basa en la relación entre las sumas de los rangos y las diferencias entre grupos.
b) Hipótesis:
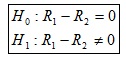
donde R es la Media de los rangos.
c) Estadístico de contraste:
Muestras pequeñas (si n<20):
![]()
Muestras grandes:
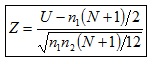
d) Distribución del estadístico de contraste. Con muestras grandes Z aproxima la distribución Normal. Con muestras pequeñas, U sigue distribución específica.
Ejemplo (con el primer grupo de datos)
b) Hipótesis:
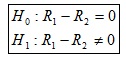
e) Estadístico de contraste:
![]()
d) Distribución del estadístico de contraste: Específica ya que las muestras son pequeñas.
e) Significación del estadístico de contraste. Según las tablas de la prueba, el estadístico es significativo para alfa=0.05.
f) Decisión: Se rechaza la Hipótesis Nula