5.1 Correlación
5.1 Inferencias respeto de r (coeficiente de correlación de Pearson)
a) Supuestos:
La población sigue la distribución Normal.
Los datos son independientes.
b) Hipótesis:
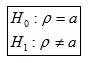
c) Estadístico de contraste:
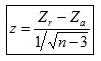
donde Zr es la transformación de Fisher del coeficiente de correlación.
d) Distribución del estadístico de contraste: Normal.
e) Significación del estadístico de contraste.
g) Intervalo de confianza:
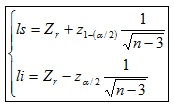
Ejemplo
En un estudio de la relación entre malestar físico subjetivo y depresión hallan que la correlación entre las dos variables es igual a 0.6 en una muestra de 35 pacientes de depresión seleccionados aleatoriamente. Saben que la correlación entre estas variables en la población de individuos sin depresión es igual a 0.4 (valor ficticio), y quieren saber si la diferencia es estadísticamente significativa.
a) Supuestos:
Se asume que los supuestos son satisfechos dado que hemos seleccionado aleatoriamente los individuos de la muestra.
b) Hipótesis:
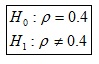
alfa=0.05
c) Estadístico de contraste:
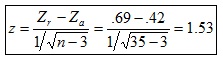
donde Zr es la transformada de Fisher del coeficiente de correlación de Pearson.
d) Distribución del estadístico de contraste: Normal.
e) Significación del estadístico de contraste: 0.06
f) Decisión: La significación del estadístivo de contraste es superior a 0.05 se acepta la Hipótesis Nula.
g) Intervalo de confianza:

Con un nivel de confianza del 95% se concluye que la correlación poblacional toma un valor entre 0.34 y 1
Conclusión: La diferencia entre la correlación observada en la muestra y la correlación poblacional no es estadísticamente significativa.