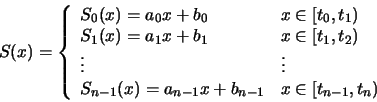Next: 7.3
Splines cúbicos Up: 7.
Interpolación Previous: 7.1
Polinomios de interpolación
7.2 Interpolación de splines
Una función spline está formada por varios polinomios,
cada uno definido sobre un subintervalo, que se unen entre sí obedeciendo
a ciertas condiciones de continuidad.
Supongamos que disponemos de n+1 puntos, a los que denominaremos
nudos, tales que  .
Supongamos además que se ha fijado un entero
.
Supongamos además que se ha fijado un entero  .
Decimos entonces que una función spline de grado k
con nudos en
.
Decimos entonces que una función spline de grado k
con nudos en 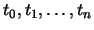 es una función S que satisface las condiciones:
es una función S que satisface las condiciones:
-
(i)
-
en cada intervalo
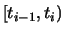 ,
S es un polinomio de grado menor o igual a k.
,
S es un polinomio de grado menor o igual a k.
-
(ii)
-
S tiene una derivada de orden (k-1) continua en
![$\left[ t_{0},t_{n} \right]$](img266.gif) .
.
Los splines de grado 0 son funciones constantes por zonas. Una forma explícita
de presentar un spline de grado 0 es la siguiente:
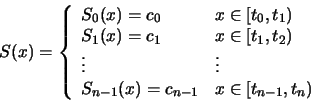
Los intervalos 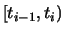 no se intersectan entre sí, por lo que no hay ambigüedad en
la definición de la función en los nudos. Un spline de grado
1 se puede definir por:
no se intersectan entre sí, por lo que no hay ambigüedad en
la definición de la función en los nudos. Un spline de grado
1 se puede definir por:
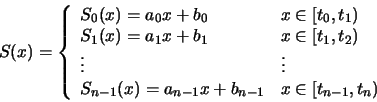
En las figuras (16) y (17)
se muestran las gráficas correspondientes a los splines de grado
cero y de grado 1 respectivamente.
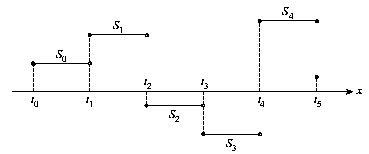
Figure: Spline de grado 0 con seis puntos.
|
[scale=1.0]eps/spline-1
|
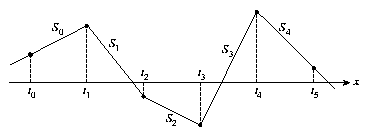
Figure: Spline de grado 1 con seis puntos.
|
[scale=1.0]eps/spline-2
|



Next: 7.3
Splines cúbicos Up: 7.
Interpolación Previous: 7.1
Polinomios de interpolación
Wladimiro Diaz Villanueva
1998-05-11
![]() .
Supongamos además que se ha fijado un entero
.
Supongamos además que se ha fijado un entero ![]() .
Decimos entonces que una función spline de grado k
con nudos en
.
Decimos entonces que una función spline de grado k
con nudos en ![]() es una función S que satisface las condiciones:
es una función S que satisface las condiciones:
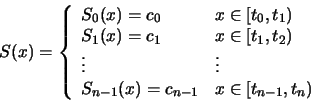
![]() no se intersectan entre sí, por lo que no hay ambigüedad en
la definición de la función en los nudos. Un spline de grado
1 se puede definir por:
no se intersectan entre sí, por lo que no hay ambigüedad en
la definición de la función en los nudos. Un spline de grado
1 se puede definir por: