DISTRIBUCIÓN GEOMÉTRICA O DE PASCAL
La distribución geométrica es un modelo adecuado para aquellos procesos en los que se repiten pruebas hasta la consecución del éxito a resultado deseado y tiene interesantes aplicaciones en los muestreos realizados de esta manera . También implica la existencia de una dicotomía de posibles resultados y la independencia de las pruebas entre sí.
Proceso experimental del que se puede hacer derivar
Esta distribución se puede hacer derivar de un proceso experimental puro o de Bernouilli en el que tengamos las siguientes características
· El proceso consta de un número no definido de pruebas o experimentos separados o separables. El proceso concluirá cuando se obtenga por primera vez el resultado deseado (éxito).
· Cada prueba puede dar dos resultados mutuamente excluyentes : A y no A
· La probabilidad de obtener un
resultado A en cada prueba es p y la de obtener un resultado no A es q
siendo (p + q = 1).
Las probabilidades p y q son constantes en todas las pruebas ,por tanto , las pruebas ,son independientes (si se trata de un proceso de "extracción" éste se llevará a , cabo con devolución del individuo extraído) .
· (Derivación de la distribución). Si en estas circunstancias aleatorizamos de forma que tomemos como variable aleatoria X = el número de pruebas necesarias para obtener por primera vez un éxito o resultado A , esta variable se distribuirá con una distribución geométrica de parámetro p.
Obtención de la función de cuantía
De lo dicho anteriormente , tendremos que la variable X es el número de pruebas necesarias para la consecución del primer éxito. De esta forma la variables aleatoria toma valores enteros a partir del uno ; í 1,2,………ý
La función de cuantía P(x) hará corresponder a cada valor de X la probabilidad de obtener el primer éxito precisamente en la X-sima prueba. Esto es , P(X) será la probabilidad del suceso obtener X-1 resultados "no A" y un éxito o resultado A en la prueba número X teniendo en cuenta que todas las pruebas son independientes y que conocemos sus probabilidades tendremos:
dado que se trata de sucesos
independientes y conocemos las probabilidades
luego la función de cuantía quedaría
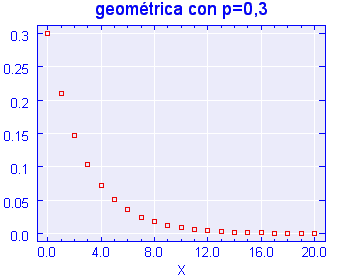
Algunos autores consideran la aleatorización como "número de pruebas anteriores al primer éxito". De esta manera el conseguir el éxito a la primera sería X=0 . En la siguiente representación gráfica de la función de cuantía de la geométrica puede apreciarse este tipo de aleatorización , sin embargo nosotros preferimos , por razones prácticas, utilizar la aleatorización antes comentada
Función de distribución
En base a la función de cuantía se
puede expresar la función de distribución de la siguiente manera.
desarrollando la expresión tendríamos
de donde
La Función Generatriz de Momentos (F.G.M.) quedaría:
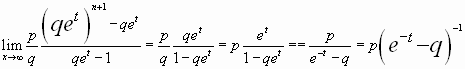
por lo que queda establecida que la F.G.M. tiene la
expresión
En base a la FGM podemos obtener la media y varianza:
Así
Haciendo t =0 tendríamos que
La varianza
sería
Haciendo t =0 tendríamos que
De esta manera
Luego 
La moda es el valor de la variable
que tiene asociada mayor probabilidad el valor de su función de cuantía es el
mayor. Es fácil comprobar (véase simplemente la representación gráfica anterior)
que 
.Por lo tanto la media de
la distribución geométrica es siempre 1.
En cuanto a la mediana Me será aquel valor de la variable en el cual la función de distribución toma el valor 0,5. Así
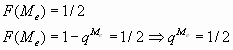
por lo que 