
ir a tratamiento de la información
Análisis cuantitativo de la información
Una parte considerable de la información económica relacionada con el mundo de la empresa o de su entorno económico es "intrínsecamente numérica" y precisa un tratamiento cuantitativo.
Tal es el caso de
toda la información expresada en unidades monetarias ( la práctica totalidad de la información contable empresarial, las principales macromagnitudes, mucha de la información financiera, algunas de las informaciones sobre el mercado, el sector, la competencia, etc....)
todas las informaciones de tipo técnico que se relacionen con la actividad económica analizada y que vengan dadas en las unidades propias de las magnitudes físicas estudiadas
toda la información interna y/o externa, agregada o no que viene expresada en términos de ratios, índices,proporciones y por tanto carece de unidades ( cotizaciones, índices bursátiles, tasas de desempleo, actividad, ocupación,cuotas de mercado,proporciones de defectos,ratios financieros, etc.)
Pero además, de una u otra forma, el hecho de que las característica estudiadas no sean , en principio, numéricas, ni impide ni minusvalora la importancia de que acaben siendo cuantificables, por medio del conteo de casos. Ello conlleva que el análisis cuantitativo o estadístico de la información no se limite exclusivamente a la información intrínsecamente numérica, sino que se extienda, también a la información "categórica" o cualitativa.
As pues el tratamiento estadístico de la
información puede y debe aplicarse a información sobre características cuantitativas
( variables) y a la información sobre características cualitativas (atributos).
La finalidad del análisis estadístico de la información suele orientarse hacia la extracción del máximo "jugo informativo" al conjunto de datos disponibles, en tres direcciones distintas pero en ocasiones curiosamente solapables.
La determinación de los rasgos esenciales de todo el conjunto de datos, eliminando lo superfluo y resaltando las características fundamentales.Todo ello con la pretensión de obtener un reducido pero significativo conjunto de indicadores globales de todo el conjunto de datos.De ello suelen ocuparse las distintas técnicas descriptivas de reducción y representación de datos.
La determinación de relaciones funcionales ( exactas) o estadísticas ( tendenciales) entre distintas características. De ello se ocupa la Regresión y la Correlación, pero también técnicas más complejas de análisis multivariante.
La determinación, aproximada en términos de certidumbre parcial, de ciertas características fundamentales sobre colectivos inabarcables por su extensión o inaccesibles por su propia naturaleza. A ello se orientaría el análisis inferencial
El diagrama de flujo que se expone a continuación , ilustra claramente estos objetivos, si bien no debemos olvidar que :
El análisis de Series Temporales no tiene por qué limitarse al estudio de única variable o atributo.
El análisis inferencial puede aplicarse a todos y cada uno de los casos

Así pues, aunque no deja de ser una simplificación, podemos convenir en que el análisis estadístico puede diferenciarse en análisis descriptivo ( realizado sobre la totalidad del colectivo) e inferencial, realizado sobre una muestra de tal colectivo, con la intención de obtener conclusiones que sean razonablemente verosímiles para la totalidad de la población.
La posibilidad de conectar ambos tipo de análisis se basa en el modelo matemático de la estadística que no es otro que el cálculo de probabilidades. En el siguiente gráfico podemos ver ilustrada esta modelización

Considerando el número de variables ( o atributos) analizados el análisis descriptivo puede diferenciarse en unidimensional y multidimensional.
Dentro del análisis unidimensional merece una mención especifica en las aplicaciones económicas de la estadística el estudio de los números índices y el análisis de series temporales
Dentro del análisis multidimensional el estudio de la dependencia estadística, la correlación y la regresión son igualmente resaltables.
Y finalmente todo ello puede considerarse en un ámbito inferencial :resolviendo el "salto" del análisis muestral a la inferencia poblacional a través de dos conjuntos de metodologías conocidas como la Estimación y el Contraste de Hipótesis.
En definitiva cualquier técnica de análisis estadístico participa de cuatro rasgos , uno de cada una de las siguientes cuatro dicotomías según los tipos de variable-dato-situación:
| ATRIBUTO | TEMPORAL | UNIDIMENSIONAL | DESCRIPTIVO |
| VARIABLE | SINCRÓNICO | MULTIDIMENSIONAL | INFERENCIAL |
Para terminar esta pequeña introducción mostramos en este gráfico las relaciones de la estadística económica con otras disciplinas y con distintos ámbitos de aplicación.

Informatización del análisis estadístico
Desde el punto procesual el análisis estadístico no implica nada más que una serie, a veces muy complicada de cálculos aritméticos.Es por ello que aunque las técnicas sean , en ocasiones complejas y requieran un esfuerzo importante para su concepción y/o comprensión, son todas ellas mecanizables con mayor o menor dificultad por procedimientos informáticos.
Algunas de las técnicas estadísticas son fácilmente ejecutables por cualquier programa ofimático medianamente sofisticado, especialmente por las hojas de cálculo comerciales.Sin embargo, otras técnicas necesitan un proceso de calculo importante y requieren un software programado específicamente para tal efecto.Este tipo particular de software se denomina "paquetes estadísticos".
Entre los paquetes estadísticos comerciales los podemos encontrar de muy variados tipos y diversas prestaciones.Algunos son ideales desde el punto de vista pedagógico como el IDP o el StatGrafics,otros facilitan una enorme variedad de herrarmientas de análisis y podemos considerarlos como "paquetes profesionales" , tal es el caso del BMDP, el SPSS, el SAS, o el TSP, este último orientado especialmente hacia el análisis econométrico ( series temporales).
En la actualidad casi todas las firmas de software que desarrollan paquetes estadísticos ofrecen versiones del producto adaptadas para ordenadores personales y sistemas operativos o entornos amigables ( como Windows, p. ej.), en este sentido la situación ha mejorado extraordinariamente en los últimos años.Igualmente casi todos los programas comerciales permiten la importación de la información desde archivos escritos en formatos convencionales de texto, hoja de cálculo o bases de datos, así como la introducción directa de la información a través de su interfaz específico.
Con todo, lo más habitual es que requieran que los datos se suministren con una estructura determinada, afortunadamente la más extendida y difundida, la estructura matricial estándar. La misma con la que habitualmente se trabaja con hojas de cálculo o bases de datos, pero requiriendo habitualmente que las columnas se correspondan con las Variables ( o atributos) [campos] y que las filas representen cada uno de los individuos disponibles [registros].
A partir de la introducción o la importación de los datos, las distintas opciones ( de menú, por ejemplo) del programa nos permitirán realizar los distintos análisis.
Obviamente, el programa no es capaz de distinguir las categorizaciones conceptuales y/o teóricos que el sentido común humano a veces realiza de forma inmediata, por ello, sulen requerirse algunos criterios de codificación, de variables y atributos y algunas normas básicas de secuencia y normalización de los análisis y de los resultados.
Entre estas normas es de destacar la normalización de salida de resultados : "ESTADÍSTICO-SIGNIFICACIÓN"
En la medida en que el programa no sabe si el cálculo de un determinado estadístico ( la mediamuestral, p.ej .) se precisa para realizar una inferencia ( estimación o contraste) o no, es bastante habitual en la utilización de las distintas técnicas que la salida de los resultados incluyan los valores de los estadísticos obtenidos junto con los demás instrumentos necesarios para la realización de inferencias: error estandar, significación asociada, intervalo del 95 %, etc.
Lo más habitual es que se muestre en los resultados el par estadístico, significación, que cabe interpretarla de la siguiente manera:
| Estadístico ( media, p.ej.) | Significación ( a ) | Observaciones (n) |
| 2.06 | 0.03 | 100 |
| Valor obtenido de la media | Significación de ese valor | número de datos |
La significación del estadístico es el valor del Nivel de Significación a partir del cual ( para valores inferiores o iguales que él) rechazaríamos la hipótesis ( habitualmente en un diseño bilateral) de que el auténtico valor del parámetro ( la media de la población, en el ejemplo) sea nulo:
H0: m=0
H1:m< >0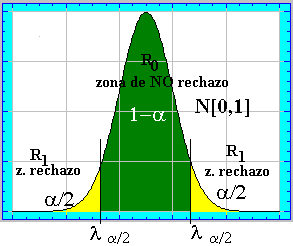
Tiene pues la interpretación alternativa de ser la probabilidad de que siendo nulo el valor del párametro se obtenga por puro azar un valor tan alto o tan bajo.Expresa en definitiva la relevancia, significación del estadístico obtenido ( en sentido inverso): Cuanto más bajo sea el valor de la significación tanto más significativo (relevante) es el valor del estadístico obtenido.
En muchas ocasiones se ofrece también en el resultado algún otro indicador complementario para la interpretación inferencial como error estandar, que permita hacer estimación o contrastes de diseño específico ( distintos del contraste simple de significación).El error estandar no es otra cosa que la desviación típica de la distribución muestral del estadístico, especialmente útil cuando el estadístico sigue una distribución normal, como es el caso de la media muestral.
| Estadístico ( media, p.ej.) | Significación ( a ) | Observaciones (n) | Error estandar |
| 2.06 | 0.03 | 100 | 0.2 |
| Valor obtenido de la media | Significación de ese valor | número de datos | Sigma/ raiz (n) |