ESTIMACIÓN
POR INTERVALOS
ESTIMACIÓN
POR INTERVALOS
1. Introducción
2. Construcción de
intervalos
2.1.
Intervalo de
confianza para la media de una población cualquiera, conocida la varianza.
ejemplo 1
2.2.
Intervalo de
confianza para la media de una población normal con varianza conocida.
ejemplo 2
2.3.
Intervalo de
Confianza para la Media de una Población Normal de Varianza desconocida
(muestras pequeñas) .
ejemplo3
2.4.
Intervalo de
confianza para la diferencia de medias con poblaciones normales y varianzas
conocidas
2.5.
Intervalo de
Confianza para la proporción de una característica.
ejemplo
4
2.6.
Intervalo de
confianza para el cociente de varianzas en poblaciones normales .
2.7.
Otros intervalos
de interés.
2.8.
Esquema de
actuación para los intervalos para la media
La "estimación por intervalo" consiste en determinar un par de valores a y b , tales que constituidos en intervalo [a ,b] ; y para una probabilidad 1-a prefijada (nivel de confianza) se verifique en relación al parámetro q a estimar se cumpla :
ó en otros términos
Podemos considerar el nivel de confianza (1-a ) que hemos prefijado para la expresión anterior como la probabilidad que existe (antes de tomar la muestra) de que el intervalo a construir a partir de la muestra incluya el verdadero valor del parámetro a estimar .Refleja la "confianza" en la "construcción" del intervalo y de que éste tras concretar la muestra contendrá el valor a estimar. De ahí que en términos numéricos dicho nivel o probabilidad haya de tomar un valor alto (0.9,0.95,0.99).
Evidentemente el complementario al nivel de confianza ; es decir a , nivel de significación supondrá las probabilidades de cometer el error de no dar por incluido el verdadero valor del parámetro a estimar en un intervalo en el que realmente si está. De ahí y dado que se trata de un error posible a cometer, su cuantificación en términos de probabilidad sea muy pequeña (0.1,0.05,0.005,..).
En relación a lo anterior .Obviamente ,cuanto mayor sea el nivel de confianza prefijado la amplitud del intervalo de estimación será también mayor y por tanto la estimación será menos precisa.
Existen para cualquier distribución una
infinidad de intervalos a los cuales les corresponde la misma probabilidad y por tanto
habrá una infinidad de intervalos , IN , que verifiquen que 
lógicamente
nosotros buscamos una estimación lo más precisa posible; es decir ,de todos los
intervalos que verifican la anterior expresión el de menor amplitud .En este sentido, es sencillo
ver que si la distribución es simétrica y unimodal ,de todos los intervalos
isoprobables, el de menor amplitud (que coincidirá con el de mayor densidad media de
probabilidad) es el intervalo centrado en la media .De acuerdo con esto ,si la
distribución que consideramos es simétrica la determinación del intervalo de
estimación es relativamente sencilla.
La construcción de intervalos específicos depende de las características de la población (normal o no ,etc.) ,de los parámetros o combinaciones de parámetros a los que se les construye (media , varianza , proporción , coeficiente de correlación , diferencias de medias , ….) , tamaño muestral y parámetros poblacionales conocidos . De ello se deduce que según dichas circunstancias la construcción de intervalos variará , si bien es cierto que el patrón de trabajo para su construcción permanece invariable.
2.- Construcción de intervalos
2.1. Intervalo de confianza para la media de una población cualquiera, conocida la varianza.
Las circunstancias específicas para la construcción de este intervalo son las siguientes :
Intervalo para m
Conocida s ( o la varianza )
Distribución poblacional desconocida.
Nivel de confianza dado 1-a
Tamaño muestral desconocido luego nos colocamos en el peor de los casos , es decir
pequeño.
Partiendo del conocido teorema de
Markov : 
donde g(x) es una función cualquiera de la variable aleatoria x , y dicha función g
está definida NO negativa,
siendo c una constante cualquiera. Así :
definiendo g(x)=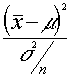 
es , evidentemente , no negativa
y tomando c=H2 tendremos en aplicación de Markov :
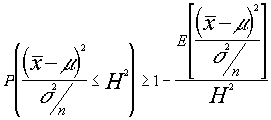dado que :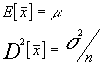 
tendremos que
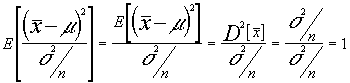
transponiendo este resultado al enunciado general :
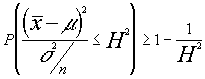tomando la raíz cuadrada tendremos
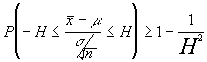despejando para
centrar el parámetro a estimar m
si queremos establecer un nivel de confianza
1-a igualaremos éste a 
d e manera que 
por lo que en función del nivel de
confianza el intervalo quedaría :
o bien :
con más de 1-a de confianza
En población cuya distribución se desconoce se obtiene una muestra (m.a.s.) de 2000 valores de la que resulta una media de 225 y una desviación típica de 10 . Suponiendo que la varianza muestral coincide con la poblacional , estimar un intervalo para la media de la población con un nivel de confianza del 95%.
Tendríamos 1-a
=0.95 luego a =0.05 ;
S=10=s ;
n=2000 ;
con 
aplicando
con más de 0.95 de
confianza.
2.2-Intervalo de confianza para la media de una población normal con varianza conocida.
Las circunstancias específicas para la construcción de este intervalo son las siguientes :
Intervalo para m
Conocida s ( o la varianza )
Distribución poblacional normal.
Nivel de confianza dado 1-a
Tamaño muestral desconocido luego nos colocamos en el peor de los casos , es decir pequeño.
Conocemos que la media muestral se distribuye
luego
tipificando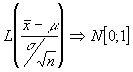 
Como se ha comentado ,al ser la
normal reducida una distribución simétrica y unimodal, el intervalo de menor amplitud y
de probabilidad
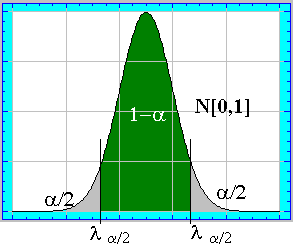
1 - a será el intervalo centrado en la media ,es decir:
el intervalo 
. Donde 
es el valor de la tabla de la
N[0 ;1] que haga que 
Es decir el valor de la normal reducida que deje a su
derecha una cola de probabilidad de a /2 Así el
valor 
será el valor simétrico de (con signo negativo) y dejará a su izquierda una cola de a /2 . De esta forma entre , 
y queda encerrada una probabilidad de 1 - a :
sería así el intervalo de menor amplitud :
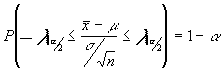despejando la media poblacional tendríamos :
nota : si el muestreo fuera sin reposición , por lo tanto no m.a.s. y si irrestricto ; el intervalo se vería afectado por el factor corrector de poblaciones finitas .Resultando , y sirva este ejemplo para comprobar lo que ocurriría en otros intervalos de otras características, de la siguiente forma :
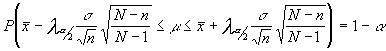siendo N el tamaño de la población.
nota :Aunque no se conozca s (desviación poblacional) si la muestra es bastante grande , n >30 es habitual considerar la desviación típica muestral , S , como si fuera la poblacional y aplicar el intervalo de estimación obtenido arriba.
Realizar la estimación de µ del ejemplo 1 considerando ahora que la población es normal
Tendríamos 1-a
=0.95 luego a =0.05 ; S=10=s
(muestra grande n>30); n=2000 ;
; población normal.
Aplicando el intervalo anterior :
el resultado sería : µ Î [224'56 , 225'44] con
el 95 % de confianza.
Las circunstancias específicas para la construcción de este intervalo son las siguientes :
Intervalo para m
desconocida s ( o la varianza )dado que n es pequeña no
podemos tomar S como s
Distribución poblacional normal.
Nivel de confianza dado 1-a
Tamaño muestral desconocido luego nos colocamos en el peor de los casos , es decir
pequeño.
Del estudio de las distribuciones muestrales conocemos
que : 
Como la distribución de t de student es una distribución simétrica , unimodal y centrada en 0 , de todos los intervalos que verifiquen que : P(t Î IN) = 1 - a el de menor amplitud será:
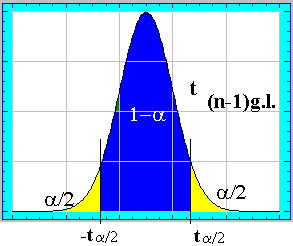
donde 
es el
correspondiente valor de la variable t para n - 1 grados de libertad y nivel de
significación a . Dicho intervalo quedaría :
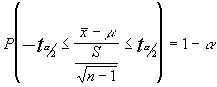para un nivel de confianza
prefijado y despejando tendríamos como intervalo
recuérdese que en el caso de muestreo irrestricto sería de aplicación el antes nombrado factor corrector de poblaciones finitas.
Las ventas diarias de cierta oficina comercial se supone que siguen una distribución normal. Para estimar el volumen medio de ventas por día se realiza una muestra de 10 días escogidos al azar ,resultando que la media de las ventas de esos 10 días es 100 u.m. con una desviación típica de 4 u.m. Dar un intervalo de estimación para el volumen medio de ventas por día con una confianza del 95 % . (ir a script de realización)
conocemos que según la información que poseemos, estamos ante:
normal ; n=10 (muestra pequeña) ; S=4(poblacional desconocida) ; media muestral=100 ;
1-a =0.95 luego a
=0.05 con lo que 
(según tabla)(ir a tabla de la t)
y dado que el intervalo a utilizar (nada dicen de irrestricto ; luego m.a.s) será
resultando :
µ Î [96'99;103'01] con el 95 % de confianza
Las circunstancias específicas para la construcción de este intervalo son las siguientes :
Intervalo para 
Conocidas 
ó desconocidas con tamaños muestrales grandes
Distribuciones poblacionales normales.
Nivel de confianza dado 1-a
Tamaños muestrales desconocidos 
luego nos colocamos en el peor de
los casos , es decir pequeño.
Conocemos que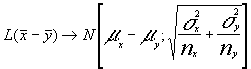 
luego la tipificando tendremos :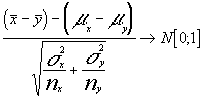 
para un nivel de confianza dado 1-a que genera los valores
extremos 
de un
intervalo centrado en dicha N[0 ;1] ; como ya vimos tendríamos :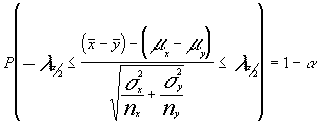
despejando :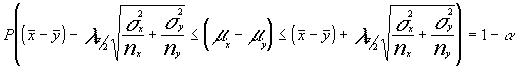 
Evidentemente y como en los casos anteriores se ha supuesto m.a.s. , en caso de irrestricto se aplicaría el f.c.p.f..
Si la varianza no fuera conocida pero la muestra fuera grande (superior a treinta , cada una) tomaríamos como varianza poblacional su homónima muestral. (ir a script de realización de este tipo de intervalo)
2.5-.Intervalo de Confianza para la proporción de una característica.
Deseamos estimar la proporción con la que se da una característica en una determinada población , esta característica es dicotómica por lo que o bien se posee o bien no . El intervalo se plantea , como todos con un nivel de confianza 1-a prefijado. Realizando , claro está, un muestreo de tamaño n , que en principio consideramos aleatorio simple.
Del estudio de las distribuciones conocemos el
comportamiento de la proporción con la que una característica
se da en la muestra : así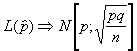 
siendo p la proporción con
la que la característica aparece en la población ;
"q" lógicamente su complementario y n el tamaño
muestral .
Tipificando obtendríamos :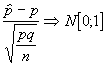 
Como en los casos anteriores y dado que
utilizamos la N[0,1] ; para un nivel de confianza dado ,1-a
, los valores de dicha normal que generan un intervalo centrado corresponderían a
por lo que quedaría el siguiente intervalo :
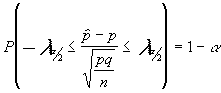despejando la proporción poblacional :
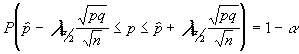
que es intervalo que estabamos buscando .
En el caso de que el muestreo fuera irrestricto su expresión sería , tras aplicar el f.c.p.f., la siguiente :
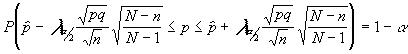
Como se ha podido comprobar en ambas expresiones de intervalo está contenida y por tanto es necesaria para su construcción la proporción poblacional "p" .Parece ilógico que si queremos estimar dicha proporción la conozcamos y por tanto la podamos utilizar . El problema puede resolverse de varias formas según el caso :
Si el tamaño muestral es muy grande podríamos utilizar
como proporciones poblacionales las obtenidas por la muestra ; es decir tomar 
en lugar de pq .
Evidentemente si el intervalo se pre-construye antes de que se realice la muestra (por
ejemplo para calcular el tamaño muestral necesario para un determinado error , como
veremos después) este no será el método aconsejable .
En una investigación comercial se muestrea a 100 individuos resultando que 25 de ellos han comprado nuestro producto .Dar un intervalo para la proporción de penetración en el mercado con una probabilidad (nivel de confianza) del 95 % .
conocemos :
1-a = 0.95 ; n=100 (grande) proporción muestral =
el intervalo sería :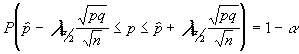
donde el valor de
= 1.96 según tabla N[0,1] (ir a tabla de la normal) y
0.95 de confianza.
Desconocemos la proporción poblacional p ; dos opciones
p=
dado que la muestra es grande ; que aplicada en el intervalo
daría que : la proporción de penetración en el mercado está entre el 16'51 % y el
33'48 % con una confianza del 95 %
(ir a script
de realización)
p=q=0.5 poniéndonos en el caso de varianza máxima ; en el caso por tanto más desfavorable. En este caso la proporción de penetración en el mercado estaría entre el 15.2% y el 34.8 con una confianza del 95% ; como se puede apreciar el intervalo tiene más holgura que el realizado por el método anterior. (ir a script de realización)
2.6-Intervalo de confianza para el cociente de varianzas en poblaciones normales .
Las circunstancias específicas para la construcción de este intervalo son las siguientes :
Intervalo para el cociente de dos varianzas poblacionales 
Realizamos dos muestras aleatorias simples de tamaños n y m
De dichas muestras se extraen las varianza muestrales 
Conocemos que las poblaciones 1 y 2 para cuya razón de varianzas queremos construir el intervalo son Normales.
Lógicamente prefijamos un nivel de confianza de 1-a .
Conocemos según vimos cuando estudiamos las distribuciones muestrales de normales que :
por el lema de Fisher - Cochran :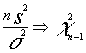
para las dos poblaciones que tenemos se dará .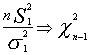
y
: 
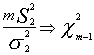
nótese que el tamaño muestral de la muestra de 1ª es n y
la de 2ª es m
dado que nos interesa la razón de varianzas y en aplicación de la expresión de la F de Snedecor:
tendremos
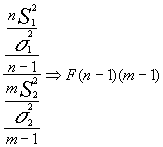arreglando el cociente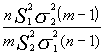 
dado que nos interesa el cociente inverso
tendríamos que:
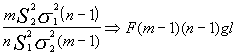
donde esta incluida la razón de varianzas para la cual queremos crear un intervalo .
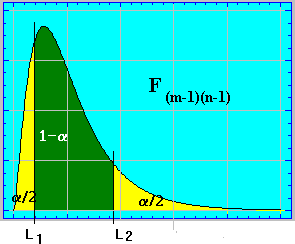
Si hemos establecido un nivel de confianza de 1-a el intervalo para una F(m-1)(n-1) vendría dado por las constantes L1 y L2 , adoptándose el criterio simplificador ,próximo al de mayor longitud , de considerar:
de manera que 
y por otra parte :
una vez determinados los valores de
L1 y L2 tendríamos el intervalo
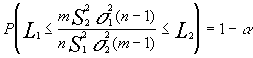despejando la razón
que nos interesa tendríamos :
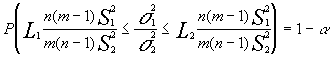
Evidentemente si plantemos medir la diferencia entre las varianzas , cuanto más próximo se la razón a la unidad menor diferencia habrá entre las varianzas y lógicamente cuando la razón entre estas difiera mucho de 1 ,la diferencia entre varianzas será mas ostensible.
2.7-Otros intervalos de interés.
Evidentemente es posible la realización o construcción de otros intervalos que pueden revestir interés . Dado que algunos son consecuencias de los ya estudiados o bien, otros, en los que su utilidad es muy ocasional , no los analizamos en profundizar . No obstante cabe destacar :
-Intervalo para la diferencia de proporciones . Su formulación es idéntica a la del de diferencia de medias teniendo la precaución de considerar como media muestral a la proporción muestral y como desviación al producto de p por q .
-Intervalo para la diferencia de medias con misma varianza poblacional .Evidentemente si bien tiene una formulación propia ,su resolución solo requiere de la utilización del antes mencionado de diferencia de medias con la precaución de que ambas desviaciones que se utilizan son lógicamente iguales.
-Intervalo para diferencia de medias con varianzas desconocidas y
muestras pequeñas. En este caso su construcción acarrearía la utilización de la t de
student cómo en el caso del de la media con varianza desconocida . Su utilidad es mínima
pues pensemos que entre ambos valores muestrales han de sumar menos de , aproximadamente,
30 lo que parece que sea un valor fácilmente superable para cualquier muestreo serio .
Si la muestra o muestras fueran grandes
( más de 30 ; lo habitual ) el intervalo pasa a ser el de varianza conocida que es
,evidentemente, el más utilizado y por ello lo hemos desarrollado .
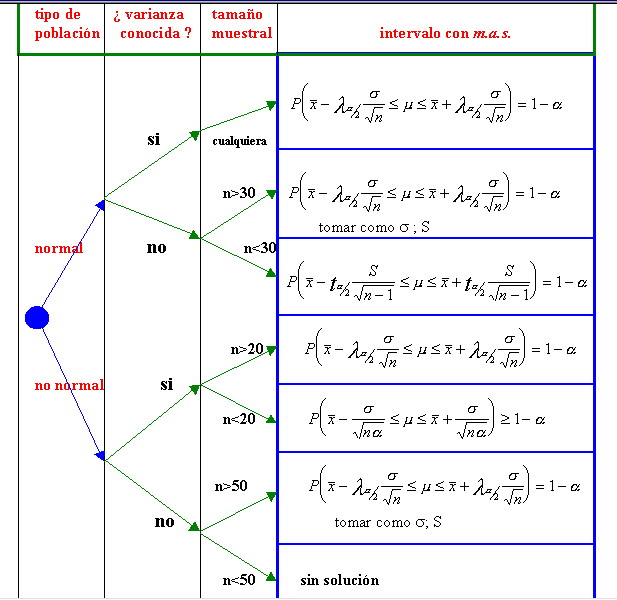
2.8.Esquema de actuación para los intervalos para la media
A modo de resumen se plantean los diversos intervalos para la media de la población según las características que se den para su construcción: así
3.Cálculo del Tamaño muestral para obtener un error de estimación prefijado
Dado un nivel de confianza 1 - a , el intervalo de
confianza para la media de una distribución normal
con varianza conocida es :
Podemos establecer el error "e" como la amplitud del intervalo es decir :
determinar
, por tanto, el tamaño muestral consistirá en:
una vez establecido el error que se quiere cometer ,despejar "n" de la
expresión que anteriormente hemos establecido :
así
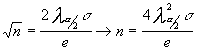
Hemos indicado que el error e , es la amplitud
del intervalo ; en muchos manuales se especifica como e=
el semi-intervalo ó la semi-holgura . Que no es más que lo mismo,
pues dos veces la semi-holgura es , evidentemente , la holgura total , por tanto su
amplitud. En otros se trata al error e como simplemente la semi-holgura ; la
semi-amplitud. Lógicamente todos los planteamientos son correctos ; solo hemos de
poner cuidado a la hora de concluir la expresión correcta del tamaño muestral .
Así : un error de e=
4 supone un error=amplitud del intervalo=8 y el
error medido como semi-amplitud sería de 4.
Para todos los intervalos que hemos visto es posible el cálculo del tamaño muestral si prefija el error admisible ; no vamos a realizar el desarrollo de todos .Nos centramos por su importancia en el tamaño muestral necesario para la construcción de un intervalo de confianza para la proporción de una característica con un determinado error prefijado , así
Si establecemos construir un intervalo de confianza para la p de una característica con un determinado nivel de confianza 1-a ; y un determinado error "e" de un tanto por uno ; y con muestreo aleatorio simple . Tendremos que :
dado que el intervalo es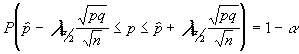
y dado que el error es e = a mplitud del intervalo = 
despejando n
obtendríamos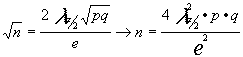 
Como es habitual el cálculo de n se realiza previamente al muestreo y precisamente se realiza el muestreo para conseguir información sobre la proporción p con la que se da una característica en una población , por lo que parece difícil que se conozca dicha p necesaria para conseguir el tamaño muestral para estimar precisamente p , de ahí que poniéndonos en el caso más desfavorable (varianza poblacional máxima) tomemos p=q=0.5 ; habitual precisión que se hace en las fichas técnicas de las encuestas.
Recurrentemente y por facilidad operativa
suele plantearse, para este tipo de cálculos de tamaños muestrales , el nivel de
confianza en el 95,5 % , la razón es que los valores de 
; (ir a tabla de la normal) por lo que para una
semi-holgura determinada de error la expresión sería la
siendo ,recordemos , 
la semi-amplitud en tanto por uno.
Calcular el tamaño muestral necesario para llevar a cabo un m.a.s. para determinar un intervalo para la proporción de personas vegetarianas si el error que estamos dispuestos a admitir es del más menos 3%. A) nivel de confianza 90%. B) nivel de confianza 95.5%.
A) e=
amplitud del intervalo
(ir a script de realización)
nivel de confianza 1-a =0.9 por
lo que (ir a tabla de la normal) 
1.645
luego tomando p=q=0.5
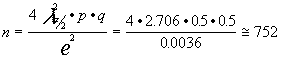
B) la semi-holgura sería 0.03 semi-amplitud (ir a script de realización)
nivel de confianza 1-a =0.995 por lo que 
(ir a tabla de la normal)
así
Si el intervalo a construir parte de un
muestreo irrestricto (sin reemplazamiento) el cálculo del tamaño muestral partiría de
la expresión: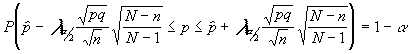 
conocido el error "e" que estamos dispuestos a conocer y conocida también la población (su tamaño), N, así como el nivel de confianza . Tendríamos que
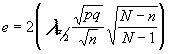de donde despejaríamos
n para conseguir el tamaño muestral. Es evidente que es mucho más cómodo despejar n
para cada caso específico que plantear una expresión general , por lo que recomendamos
que así se haga . Las afirmaciones que se vertieron sobre "p" y su valor en el
caso de m.a.s. son de aplicación , también ,en este caso. (ir a script de realización para p=q=0.5)
(ir a script de
realización para información sobre p)