La teoría física. Todo gira, pero: ¿tienes un momento?

La teoría que explica los siguientes pasos de la formación planetaria es, en sus rasgos básicos, bastante antigua. Data del siglo XVIII y fue propuesta por primera vez por el filósofo Inmanuel Kant (1724-1804) de manera cualitativa. Y posteriormente fue arropada analíticamente por Pierre Simon de Laplace (1749-1827). En síntesis la "teoría nebular" de Laplace de la formación del Sistema Solar nos cuenta cómo una nebulosa se contrajo bajo la influencia de su propia gravitación y su velocidad rotacional aumentó hasta que colapsó en un disco, en el cual se formarían los planetas. Este sencillo modelo explica toda un serie de curiosas coincidencias que se dan en nuestro Sistema Solar, y que tanto sorprendían a los científicos del s. XVIII:

1. Las órbitas de los planetas están todas casi en el mismo plano que la órbita de la Tierra, llamado el plano de la eclíptica, que es además el plano ecuatorial del Sol.
2. Las órbitas son esencialmente circulares, elipses de excentricidad muy baja, con la excepción de Plutón, descubierto en 1930, que es considerado un planeta más por cuestiones políticas que astronómicas.
3. Todos los planetas y satélites tienen el mismo sentido de rotación (denominado directo) alrededor de su cuerpo central, y alrededor de sí mismos (salvo alguna excepción), al igual que el Sol. Además, la práctica mayoría de los asteroides y la mayor parte de los cometas giran también alrededor del Sol en sentido directo.

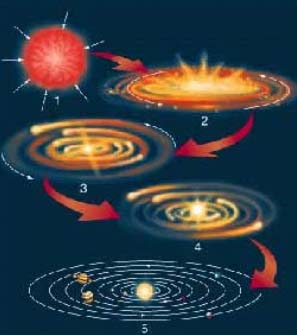
Foto: Ilustración de la "teoría nebular" de Laplace de la formación del Sistema Solar.


Este modelo tenía el mérito de explicar todas las coincidencias de la lista anterior y estaba en todo de acuerdo con la mecánica newtoniana. Sin embargo, dos grandes objeciones al modelo aparecieron a finales del siglo XIX. En primer lugar, James Clarke Maxwell (1831-1879) demostró que, según estaba establecido el modelo de Laplace, era difícil explicar la acreción de un planeta a partir de un anillo de planetoides: más bien debería dar lugar a discos. La segunda objeción se refería al problema del momento angular.

¿Qué es el momento angular? Partamos primero del concepto de momento lineal (también llamado cantidad de movimiento o ímpetu) usualmente representado por la letra p. Esta magnitud se define como el producto de la masa de un cuerpo por su velocidad: p = m v. Puesto que la velocidad es un vector (una magnitud en la que importa su valor y su dirección), el momento lineal también lo es. El momento lineal nos proporciona una idea matemática de la noción intuitiva de inercia: si no hay fuerzas exteriores, el momento lineal se conservará sin cambios. Esto quiere decir que el producto de la masa y la velocidad, ese valor numérico, no cambiará. Como las masas habitualmente no cambian, esto, en el día a día, quiere decir que la velocidad no cambia. Pero no solo eso: como el momento lineal es un vector tampoco cambiará su dirección. Por tanto, un cuerpo que se traslade y no esté sometido a fuerzas externas, continuará moviéndose en línea recta sin variar su trayectoria y sin detenerse.