Motivar en clase a través de problemas actuales
Resumen
“Las matemáticas son el lenguaje en el que Dios escribió el universo”. Estas célebres palabras dichas por Galileo nos recuerdan una verdad fundamental: las matemáticas aparecen por todos lados. Más allá de los clásicos ejemplos que motivan el uso de las matemáticas, cabe preguntarse: ¿pueden sernos útiles los problemas actuales? En este trabajo expondremos como hemos tratado de motivar al alumnado a entender mejor y a disfrutar con las matemáticas mediante uno de los proyectos más futuristas de nuestra época: el Hyperloop.
Palabras clave
Tecnología, Aprendizaje de matemáticas.
Abstract
“Mathematics is the language in which God wrote the universe.” These famous words spoken by Galileo remind us of a fundamental truth: mathematics is everywhere. Beyond the classic examples that motivate the use of mathematics, it is worth asking: what about today’s problems? Can they not be useful? We will analyze how students can be motivated to learn and enjoy mathematics through one of the most futuristic projects of our time: the Hyperloop.
Keywords
Technology, Mathematics learning.
Introducción
La formación integral de profesionales cualificados es el principal objetivo de la enseñanza universitaria. Para ello, El Real Decreto 1125/2003, de 5 de septiembre, publicado el 18 de septiembre de 2013 en el Boletín Oficial del Estado (BOE) [1], así como sus sucesivos ajustes, establece en las titulaciones universitarias oficiales de Grado un sistema europeo de créditos (ECTS), que se estructuran a través de asignaturas en las diferentes áreas de conocimiento, adecuadas a cada perfil. Los contenidos de estas asignaturas se definen en base a competencias científicas que permitan al alumnado desarrollar con éxito su actividad profesional. Por tanto, es muy relevante que los alumnos adquieran dichas competencias al superar las asignaturas, es decir, demuestren los conocimientos, las habilidades y actitudes, transversales y específicas, asociados a cada una de ellas. Para facilitar este proceso, especialmente en materias básicas como las matemáticas, es importante elegir una metodología docente adecuada.
Actualmente, la tecnología empieza a introducirse desde la educación primaria en las aulas, cada vez más instituciones dinamizan la enseñanza mediante el uso de proyectos donde se trabajan problemas realistas, a través de dispositivos y simulaciones disponibles, gracias a la democratización de las nuevas tecnologías (TIC) en nuestra sociedad.
En los niveles de educación superior, prácticamente la totalidad del alumnado maneja con soltura aplicaciones o programas informáticos, que facilitan visualizar ejemplos prácticos que facilitan su aprendizaje y aumentan la motivación, siempre y cuando se consiga despertar el interés del alumno por la utilidad de los conocimientos que pretendemos transmitir.
En este sentido, parece una opción interesante utilizar un proyecto como Hyperloop [2], para involucrar a los estudiantes de los grados de ingeniería en asignaturas como matemáticas, física o química, materias básicas en todos los grados de esta rama, que en general les resultan demasiado teóricas y poco relacionadas con sus intereses profesionales.
Hyperloop es un concepto de transporte, formulado por el célebre Elon Musk, que combina la velocidad y el alcance de un avión con el consumo energético y la infraestructura de un tren. Está basado principalmente en el transporte de cápsulas que levitan mediante fuerzas electromagnéticas dentro de túneles a baja presión, las cuales tendrían instalado un compresor (turbina) para evitar problemas asociados con la presión del aire a velocidades cercanas a la del sonido. La Universitat Politècnica de València (UPV) es, desde hace varios años, hogar de uno de los equipos universitarios más punteros del mundo en el desarrollo de prototipos Hyperloop a pequeña escala, algo fundamental para probar y asentar la tecnología necesaria para diseñar prototipos a tamaño real.
El objetivo principal de este trabajo consiste en mostrar a los alumnos del Grado de Ingeniería Mecánica de la Escuela Técnica Superior de Ingeniería del Diseño (ETSID) de la UPV, cómo los contenidos impartidos en la asignatura Matemáticas I tienen múltiples aplicaciones en su área de interés, utilizando el desarrollo de prototipos como Hyperloop. Se ha propuesto motivar el aprendizaje del concepto de curva de interpolación y algunas técnicas de cálculo a partir de la modelización de un problema real. Los estudiantes llegan a conclusiones acerca de la necesidad de conocer la teoría y las técnicas de interpolación y, pese a que la modelización matemática del problema puede haberles sido difícil en un principio, con un poco de ayuda consiguen realizar una modelización buena acerca del problema a tratar.
Sin embargo, consideramos que este trabajo puede ser extrapolado a otros grados, ya que el equipo Hyperloop de la UPV está formado por 46 personas de todas las áreas del conocimiento, desde ingenieros aeroespaciales, mecánicos, electrónicos, matemáticos hasta graduados en bellas artes y economía.
Metodología
Técnicas empleadas
Nuestro objetivo de motivar al alumno a través de la resolución de problemas aplicados, lo llevamos a cabo principalmente en las prácticas de la asignatura, donde utilizamos el programa Mathematica de Wolfram [3], ya que con la ayuda de este software podemos resolver de forma mucho más rápida y visual los problemas planteados, integrando fácilmente los conocimientos impartidos en la teoría de la asignatura.
La elección de este programa, responde a dos motivos principales:
La UPV tiene acceso a este software con una licencia de campus y todos los alumnos tienen la posibilidad de descargarse una versión de alumno de Mathematica, con la que pueden practicar de forma no presencial en sus propios ordenadores.
Mathematica es un software muy versátil, con sintaxis bastante intuitiva y mucha información en la ayuda, por lo que resulta una interesante herramienta de cálculo para la realización y comprobación de ejercicios y problemas. Además ofrece muchas posibilidades para las representaciones gráficas, aspecto que ayuda mucho a la hora de visualizar los ejemplos.
Utilizamos las prácticas informáticas, principalmente, para facilitar la resolución de problemas con cálculos largos o excesivamente complicados planteados en clase, con el objetivo de que el alumno afiance los conocimientos adquiridos en la materia y aprenda el correcto manejo del programa.
En nuestro caso, pretendemos además encontrar la conexión entre la teoría explicada en la asignatura y problemas “realistas” que muestren a los alumnos la aplicación de esta en sus áreas de interés profesional. Para ello, empezamos cada práctica presentando los comandos específicos de Mathematica que utilizaremos en el desarrollo de los ejercicios, para realizar, a continuación, algunos ejemplos y plantear ejercicios relacionados con el tema tratado, que tengan una aplicación lo más actual posible de los contenidos trabajados.
Como ejemplo, mostraremos un caso práctico que utilizamos en clase a mediados del segundo cuatrimestre, en la parte del temario correspondiente al álgebra lineal, donde trabajamos los sistemas de ecuaciones lineales, así como la obtención de sus posibles soluciones. En particular, cuando trabajamos con sistemas incompatibles, es decir, sin solución, introducimos el método de mínimos cuadrados para obtener el mejor resultado posible. En este mismo contexto, podemos encontrar la regresión lineal, que supone encontrar los coeficientes que permiten aproximar, por una recta, una serie de puntos de una manera óptima.
Para aplicar estos conceptos en los prototipos de Hyperloop, consideramos que como en todo vehículo móvil, las irregularidades del terreno por el que debe circular provocan vibraciones y oscilaciones indeseadas. Para ello, se deben instalar amortiguadores y muelles, tanto para mejorar el confort de los viajeros como por la integridad de la estructura en sí misma del prototipo. En la Figura 1 se puede observar el sistema de control vertical diseñado e instalado en el prototipo IGNIS.

La Figura 2 muestra cómo actúa el sistema en su conjunto ante una perturbación en el raíl.
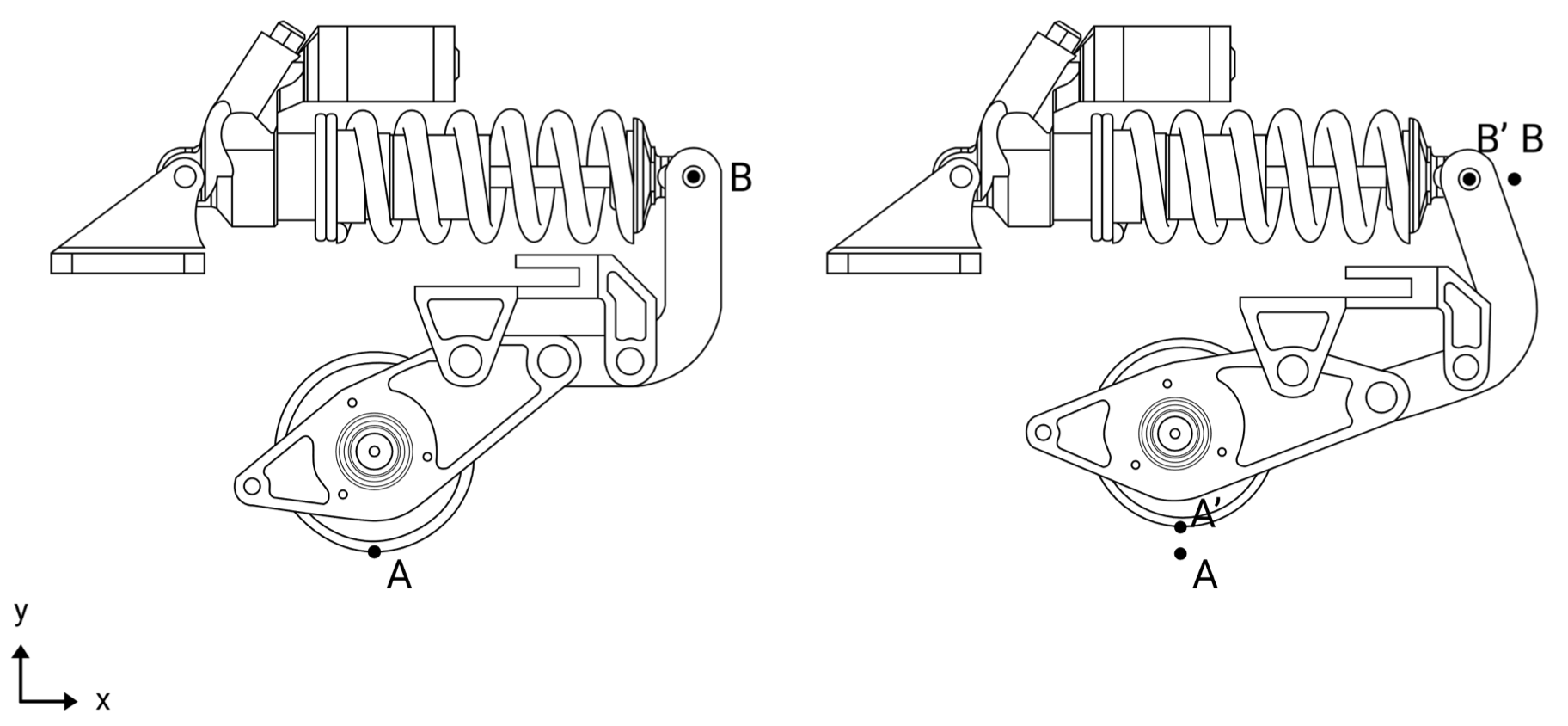
Aunque hay varias maneras de abordar este problema, una de ellas es utilizar geometría básica, para calcular cómo afecta una deformación vertical en la rueda a la deformación en el muelle. Para saber si un determinado muelle es útil para nuestro propósito, es necesario comprobar cómo actúan las fuerzas en él y debemos realizar un experimento de compresión en todos los muelles que pretendamos utilizar en este tipo de diseño.
Para realizar dicho experimente es necesario comprimir y descomprimir el muelle varias veces, con el objetivo de recoger los datos de la fuerza que ha ejercido en cada momento. Estos datos se reflejan en una gráfica como la de la Figura 3.
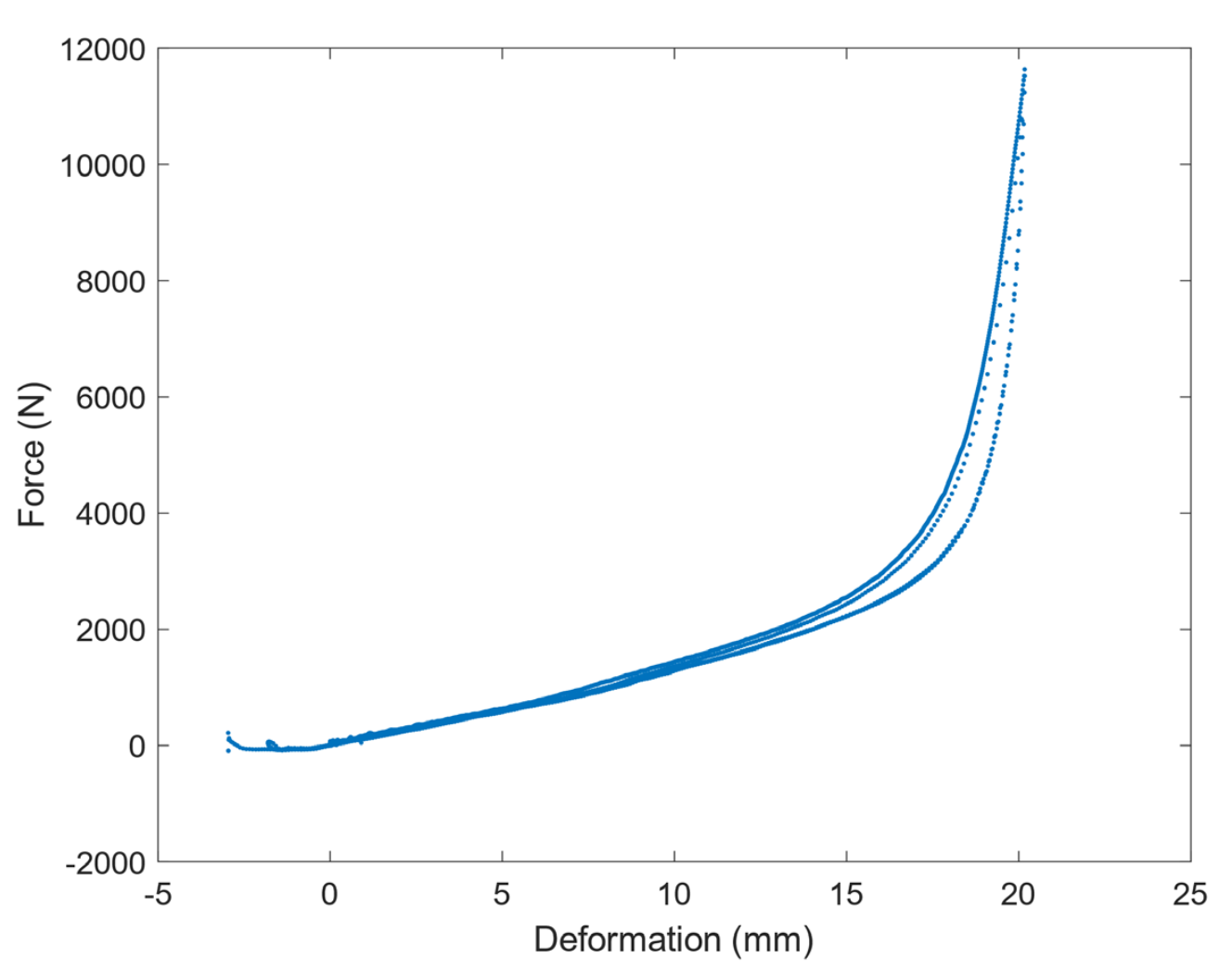
Con estos datos, el alumno deberá realizar un ajuste polinómico por mínimos cuadrados y ver qué grado de polinomio le permite obtener un buen ajuste.
Una versión más sofisticada de este problema, que se puede plantear para los alumnos interesados en el tema, consiste en preparar una función suplementaria para que, dado el ajuste obtenido pueda ver cómo afecta una elección u otra en las fuerzas tangenciales y normales del muelle y, estas a su vez, a la dinámica general del prototipo que estamos analizando.
Resultados
Para evaluar esta metodología y su influencia en la adquisición de las competencias asociadas a la asignatura, hemos planteado una encuesta a los 29 alumnos del grupo de la tarde, para ver si esta actividad les ha ayudado en la asignatura de Matemáticas I. Hemos obtenido la respuesta de 9 de los 29 alumnos, es decir, aproximadamente de un 31% del grupo.
La encuesta consiste en un formulario on-line elaborado con la herramienta Google Docs, utilizando una Escala de Likert como medida, ya que según J. C Nunnally [4] las escalas sumativas constituyen el mejor método para el escalamiento de actitudes verbalizadas.
Para elaborar dicho formulario, hemos extraído de la guía docente [5] las competencias genéricas y específicas propias de la materia y hemos pedido a los alumnos que puntúen en qué medida piensan que la metodología utilizada en la asignatura Matemáticas I ha contribuido a adquirir cada una de estas competencias según el baremo 1=Nada, 5=Mucho [6, 7].
En concreto, se han valorado las competencias listadas en la Tabla 1, donde hemos asignado un código que utilizaremos en las siguiente gráfica.
| Competencia | Código |
|---|---|
| Resolución de problemas matemáticos que puedan plantearse en la ingeniería | c1 |
| Conocimiento en materias básicas y tecnológicas | c2 |
| Capacidad de resolver problemas, razonamiento crítico y transmitir conocimientos, habilidades y destrezas en Ingeniería Industrial | c3 |
| Capacidad de integrarse y colaborar en un entorno multidisciplinar | c4 |
En este mismo cuestionario hemos incluido un texto libre: “Describe las competencias que en tu opinión debería aportar la asignatura de Matemáticas I y si crees que las has alcanzado con la metodología aplicada”.
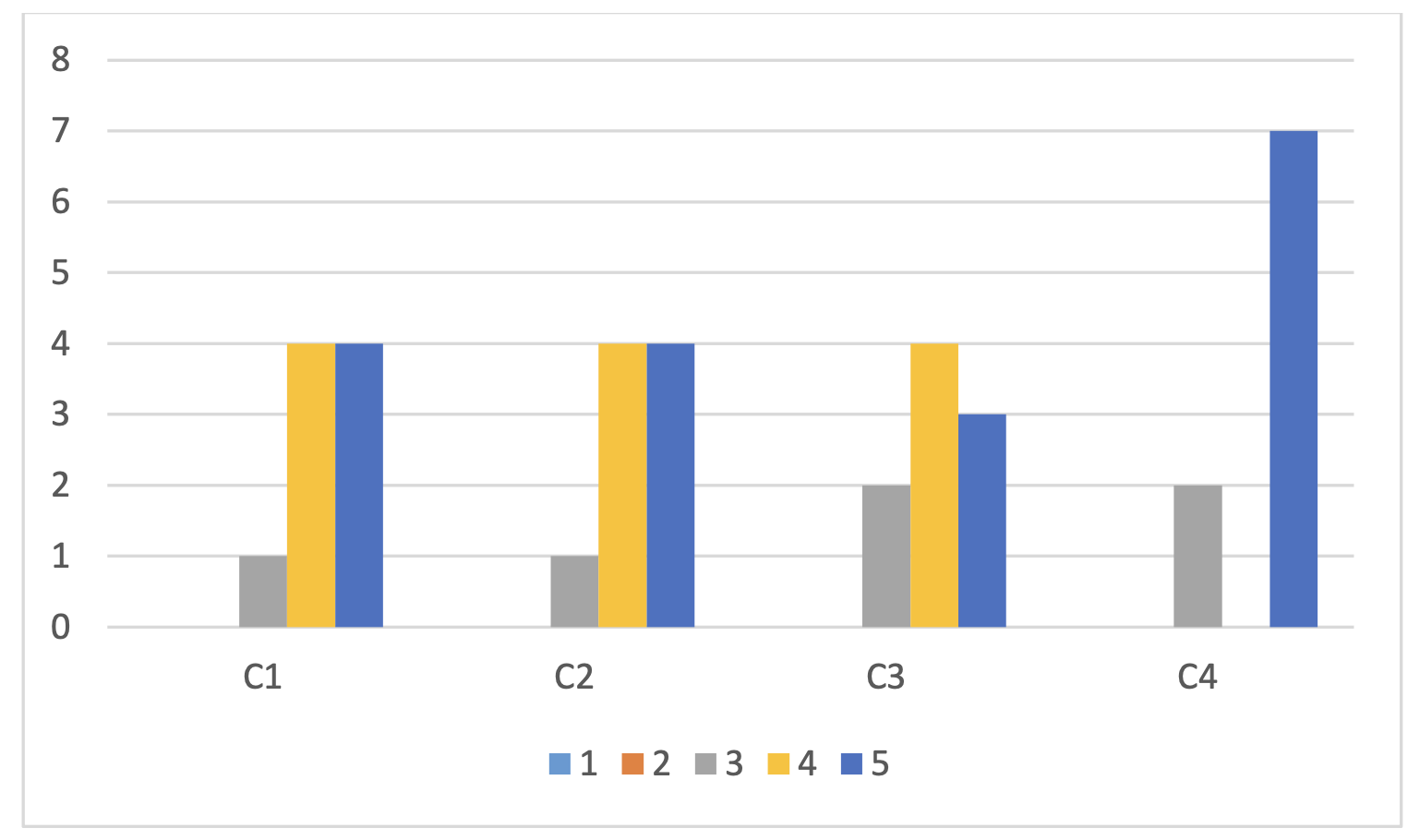
En la Figura 4 podemos observar la frecuencia obtenida para cada una de las competencias. En general el alumnado está satisfecho con las competencias adquiridas puesto que la mayor frecuencia de puntuaciones está en el 4 y el 5.
Transcribimos a continuación algunas de las respuestas obtenidas en la pregunta abierta del formulario y observamos que, en general, los alumnos están satisfechos con su adquisición de competencias, así como con la metodología utilizada, como indican los siguientes comentarios:
“Debería ayudar al desarrollo de la lógica para resolver problemas, y en este caso lo ha conseguido”
“Aprender a resolver problemas por uno mismo y encontrar nuevas maneras para ello, sí lo he aprendido”
“Si creo que he alcanzado todas las competencias que se enseñan en la asignatura gracias a la manera metodología aplicada y a todos materiales que se han puesto a nuestra disposición”
“En mi opinión, las matemáticas deben ser útiles para la resolución de problemas relacionados con la ingeniería. Y en este curso hemos podido adquirir conocimientos que nos son útiles en nuestra carrera para resolver problemas más complejos”.
Aunque se ha considerado insuficiente el tratamiento de algunos tópicos como indica el comentario: “Me ha faltado un poco de integrales, pero por lo demás ha estado muy bien”.
Conclusiones
Del análisis realizado de nuestra propuesta inicial, podemos concluir que existe un elevado grado de satisfacción del alumnado con la metodología empleada para transmitir las aplicaciones prácticas de los conocimientos de la asignatura, independientemente de la competencia que se evalúe.
A pesar de todo, queda patente que es necesario hacer mayor hincapié en algunos temas y aumentar en lo posible el uso de problemas actuales para justificar la aplicación práctica de los métodos matemáticos explicados en la asignatura, debido a la evidente necesidad de conexión del graduado en ingeniería mecánica con las necesidades del mundo real.
Referencias
[1] BOE-A-2003-17643. Real Decreto 1125/2003. Página web [Consulta: 16 de julio de 2021]
[2] Universitat Politècnica de València. Hyperloop. Página web [Consulta: 16 de julio de 2021]
[3] Wolfram. Página web: Wolfram: Computation Meets Knowledge [Consulta: 16 de julio de 2021]
[4] Nunnally, J. C., Psychometric Theory, Mac Graw-Hill, New York, (1987).
[5] Universitat Politècnica de València. Grado en Ingeniería Mecánica. Guía Docente Matemáticas I (curso 2019-2020). Página web [Consulta: 16 de julio de 2021]
[6] Morales Vallejo P., Guía para construir escalas de actitudes, Universidad Pontificia Comillas, Madrid, (2010).
[7] Briones G., Métodos y Técnicas de Investigación para las Ciencias Sociales, Trillas, México, (1995).