La enseñanza de la teoría de grafos a través de la modelización
Resumen
La enseñanza de la teoría de grafos, debido a su gran aplicabilidad, puede abordarse de formas muy distintas. En demasiadas ocasiones, seguir una metodología “tradicional” fomenta que los alumnos adopten un papel pasivo en el aula, que les lleva a ser meros receptores de contenidos sin aparente vinculación con la realidad, ni espíritu crítico. Con el objetivo de mejorar esta situación, consideramos que cambiar el enfoque es una buena opción para aumentar el interés y la motivación por las matemáticas, haciendo las clases más amenas. Para ello, planteamos problemas de la vida cotidiana cuya solución nos facilite introducir los diferentes conceptos de grafos. De esta manera, se inicia a los estudiantes en el campo de la modelización y la teoría de grafos simultáneamente. En este trabajo presentamos líneas de actuación para poner en práctica este enfoque más aplicado, aportando varios ejemplos concretos.
Palabras clave
Metodología, modelización matemática, teoría de grafos.
Abstract
The teaching of graph theory, due to its great applicability, can be approached in many different ways. On too many occasions, following a “traditional” methodology encourages students to adopt a passive role in the classroom, which leads them to be mere receivers of content with no apparent link to reality or critical spirit. To improve this situation, we believe that changing the approach is an excellent option to increase interest and motivation for mathematics, making the classes more enjoyable. To do this, we pose problems from everyday life whose solution helps us to introduce the different concepts of graphs. In this way, we simultaneously introduce students to modelling and graph theory. This paper presents lines of action to put this more applied approach into practice, providing several concrete examples.
Keywords
Methodology, mathematical modelling, graph theory.
Introducción
El cambio de paradigma experimentado por el sistema educativo en las últimas décadas, impulsado por el acceso a la tecnológica en las aulas, la adaptación pedagógica del conocimiento neurocientífico y las sucesivas políticas reguladoras, entre otros muchos factores, ha propiciado la evolución de la enseñanza universitaria hacia una interconexión más profunda con la sociedad actual.
Sin perder de vista el principal objetivo de los estudios universitarios: formar profesionales cualificados que desarrollen con éxito su actividad profesional, las universidades han pasado de diseñar titulaciones describiendo los contenidos mínimos necesarios, a establecer las competencias específicas y transversales que deben dominar los futuros graduados.
La adaptación a este proceso, especialmente en materias básicas como las matemáticas, requiere diseñar una metodología y evaluación coherentes con este nuevo enfoque. En este artículo, repasaremos los cambios experimentados tanto en la metodología, como en la evaluación de las asignaturas en las que se imparte teoría de grafos, en las sucesivas titulaciones en Ingeniería Informática de la Escuela Técnica Superior de Ingeniería Informática (ETSINF) de la Universitat Politècnica de València (UPV).
Metodología
Desde 1985 la teoría de grafos está integrada en la materia de matemáticas de los distintos planes de estudios de la titulación en Ingeniería Informática de la ETSINF de la UPV.
Inicialmente, su estudio tenía una fuerte componente teórica y formal, por lo que se impartía con clase magistral, donde se demostraban las propiedades y se analizaban con todo detalle las trazas de los algoritmos estudiados. La participación de los alumnos en las clases era escasa y se realizaban ejercicios principalmente teóricos.
Los nuevos planes de estudio, en la década de los 90, incorporaron prácticas en las asignaturas y aprovechando el gran potencial de los grafos a la hora de resolver problemas reales, empezamos a plantear aplicaciones prácticas para trabajarlas con los alumnos en las sesiones de laboratorio. Inicialmente, se daba mucho más peso a la correcta resolución del problema, aplicando el algoritmo adecuado, que a la modelización del mismo.
Debido a la sucesiva democratización de las nuevas tecnologías (TIC), y que prácticamente la totalidad del alumnado de la UPV, en particular del perfil de nuestra titulación, tenía acceso a un ordenador y manejaba con soltura aplicaciones y programas informáticos, empezamos a pensar en utilizar a nuestro favor estas herramientas. Así, comenzamos a utilizar software específico en las prácticas para resolver de forma rápida y visual los problemas de modelización planteados. Empezamos utilizando Mathematica de Wolfram [1], pero actualmente lo hemos reemplazado por SWGraphs [2], mucho más sencillo de manejar y de acceso libre.
Por otra parte, los sucesivos cambios en los planes de estudio, condujeron a una reducción de créditos en nuestras asignaturas y, como consecuencia, también en los contenidos correspondientes a la teoría de grafos.
Como consecuencia de todo ello, hemos ido integrando los conocimientos teóricos impartidos en la asignatura con aplicaciones de estos al mundo real, de forma mucho más sistemática y efectiva, con el objetivo de motivar al alumno a través de la resolución de problemas aplicados, centrando nuestra atención en el aprendizaje de los estudiantes, de manera que la modelización pasó a tener un peso mayor en nuestra metodología.
Observando que los alumnos no aprenden de forma aislada, sino que relacionan las ideas que les presentamos con las que ya conocen [3], resulta interesante utilizar la modelización para cimentar los nuevos conocimientos que les presentamos en nuestras asignaturas, empleando situaciones que tengan sentido para ellos y que se ajusten lo máximo posible a sus intereses para mantenerlos motivados.
Conviene empezar utilizando modelos simples de los nuevos conceptos, aumentando la dificultad a medida que la comprensión del alumno y la complejidad de la materia vayan aumentando.
Para ilustrar esta metodología, plantearemos una serie de situaciones que utilizamos en nuestras aulas. La primera de ellas representa una situación que es posible modelizar a través de un grafo no dirigido, introduciendo de esta manera el nuevo concepto y los elementos que lo caracterizan.
Problema 1
La profesora de Matemática Discreta quiere hacer grupos de 9 alumnos para realizar un proyecto.
El primero de estos grupos está formado por: Marta, Sergio, Lidia, Irene, Eloy, Alicia, Carlos, Francisco y Guille.
Algunos chicos ya eran amigos antes de empezar el curso, concretamente: Marta es amiga de Sergio, Eloy e Irene.
- Sergio de Lidia, Alicia, Marta y Guille.
- Lidia de Sergio y Alicia.
- Alicia de Lidia, Sergio y Guille.
- Eloy de Marta, Irene, Carlos y Guille.
- Carlos de Eloy y Guille.
- Guille de Sergio, Alicia, Francisco, Carlos y Eloy y, finalmente, Francisco de Guille.
Para que sea más fácil saber en un momento dado quién es amigo de quién, ¿cómo podrías representar la situación de forma más clara? Los alumnos proponen en general, dos posibilidades, relacionando a los amigos de forma gráfica, o bien, utilizando una tabla, como vemos en la Figura 1:
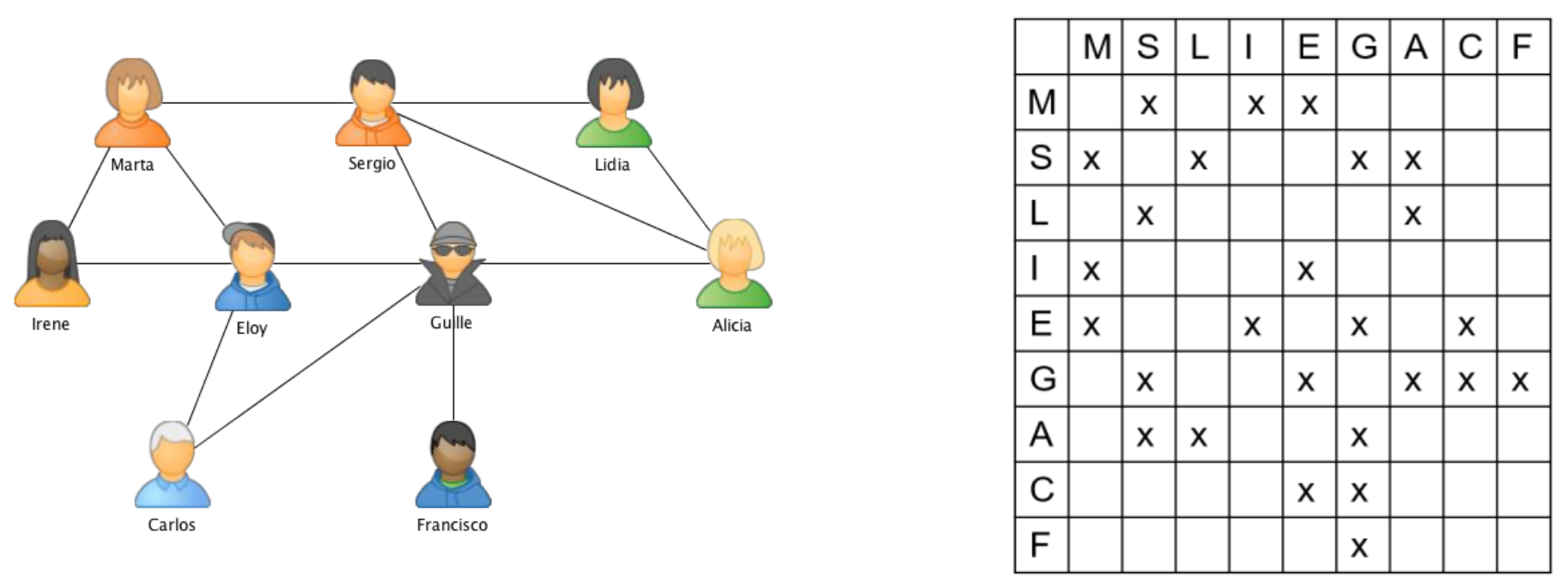
Esto nos permite introducir el concepto de grafo y modelizar el problema considerando como el conjunto de vértices que lo definen (V) a los alumnos y como aristas (E) los pares ordenados que determinan la relación de amistad entre ellos, es decir: \[ \begin{align*} V&=\{\mathrm{Marta, Sergio, Lidia, Irene, Eloy, Guille, Alicia, Carlos, Francisco} \} \\ E&=\{(u,v) \mid u,v \in V, u \mbox{ es amigo de } v\} \end{align*} \]
Notamos que la información del grafo se puede representar de forma gráfica o mediante la matriz de adyacencia, que en el caso de grafos no dirigidos es simétrica, como vemos a continuación:
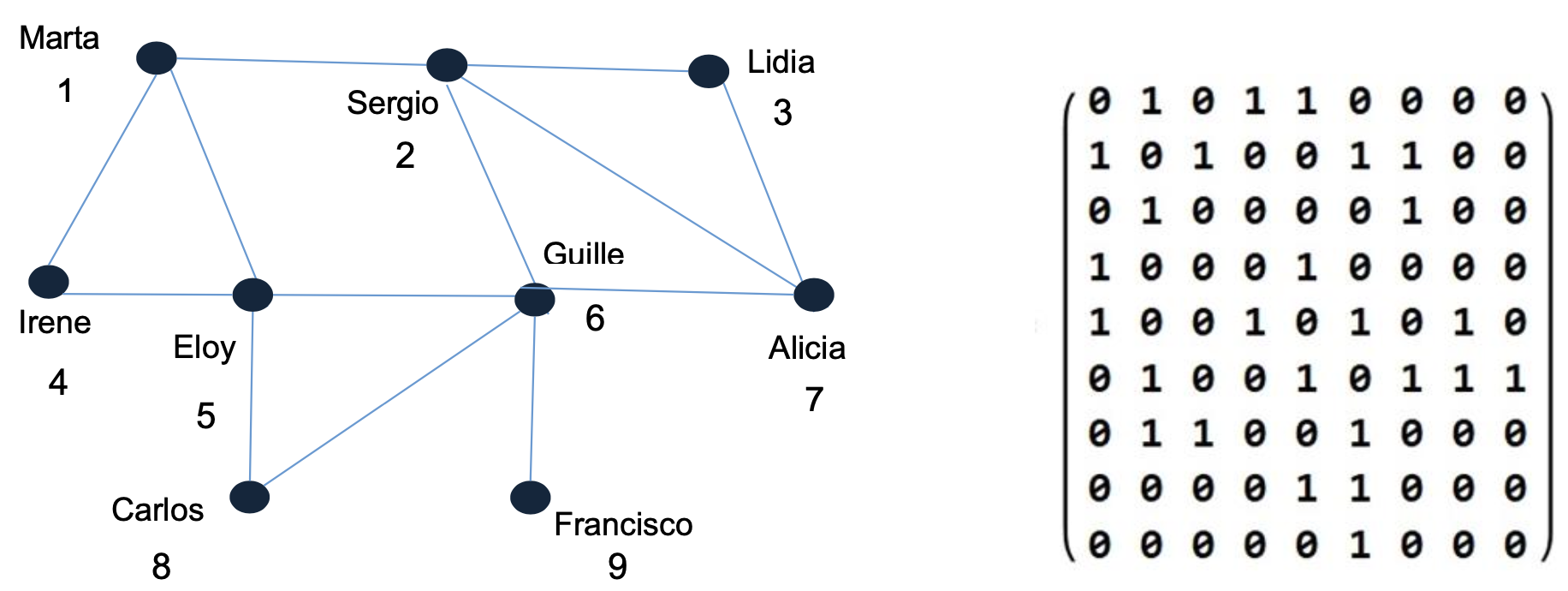
Una vez definido el grafo, podemos introducir el concepto de grado de un vértice, relacionándolo, por ejemplo, con el número de amigos que tiene cada alumno. En general buscamos situaciones cotidianas que nos facilitan la explicación tanto de los diferentes tipos de grafos, como de sus principales propiedades, como por ejemplo la propiedad de los grafos no dirigidos: el número de vértices de grado impar es par, como se muestra a continuación:

Podemos motivar el uso de esta propiedad en el problema anterior, planteando si es posible elegir parejas de alumnos, que sean amigos, para hacer un trabajo. Utilizando la siguiente situación, introducimos el concepto de grafo dirigido:
Problema 2
Se está diseñando una pequeña urbanización de adosados. Como innovación han decidido que los cruces de las calles sean pequeñas placitas, lo que da sensación de amplitud. Uno de los puntos a estudiar es el sentido de la circulación vial en cada uno de los tramos.
El concejal de urbanismo nos propone la siguiente opción, donde P. significa plaza: de la P.1 hacia la 2 y la 9, de la P.2 hacia la 3, 7 y 9, de la P.3 hacia la 4 y la 6, de la P.4 hacia la 3, de la P.5 hacia la 4, de la P.6 hacia la 4, 5 y 7, de la P.7 hacia la 8 y finalmente de la P.9 hacia la 8. ¿Cómo representaríamos un mapa de la urbanización?
En este caso, la situación se puede modelizar como muestra la Figura 3, y podríamos trabajar conceptos como accesibilidad, conexión, aristas de corte, orientabilidad, etc., a través de preguntas del tipo:
¿Se podrá llegar de la plaza 1 a las demás? ¿Y desde la 6?
¿Qué opinas del plan de circulación ideado por el concejal? ¿Crees que es adecuado? ¿Puedes diseñar uno mejor?
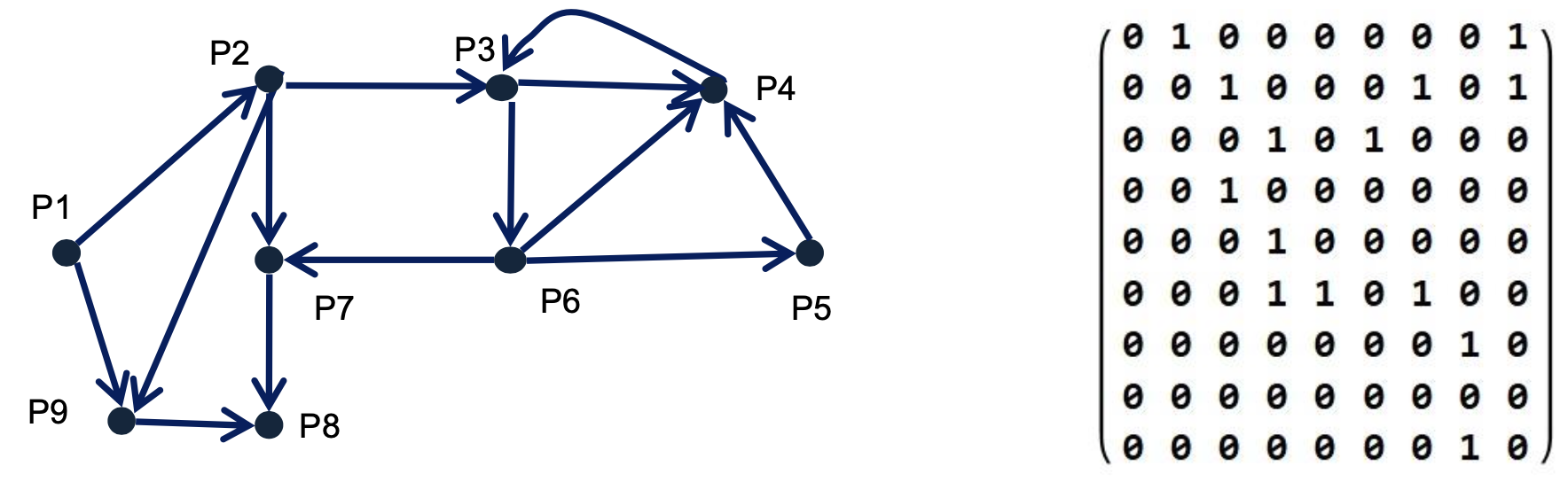
Por otro lado, debemos potenciar que los alumnos no se limiten a aplicar los algoritmos en los grafos que modelizan el problema, sino que analicen las diferentes situaciones (o restricciones) que aparezcan en un mismo problema, simplifiquen al máximo los grafos antes de aplicar los algoritmos y comprueben las hipótesis necesarias antes de aplicar cada uno de ellos.
Para ilustrar esto podemos plantear la siguiente situación, donde aparecen diferentes restricciones del problema planteado inicialmente, lo que conduce a la utilización de diferentes conceptos y algoritmos en un mismo problema.
Problema 3
Se han inaugurado dos grandes supermercados de la cadena PrecioJusto, en las cercanías de ocho poblaciones que reciben una gran cantidad de turistas cada verano. Podemos ver un mapa de la zona en la figura, donde los números representan los kilómetros entre las poblaciones, o las poblaciones y los supermercados PrecioJusto, respectivamente.
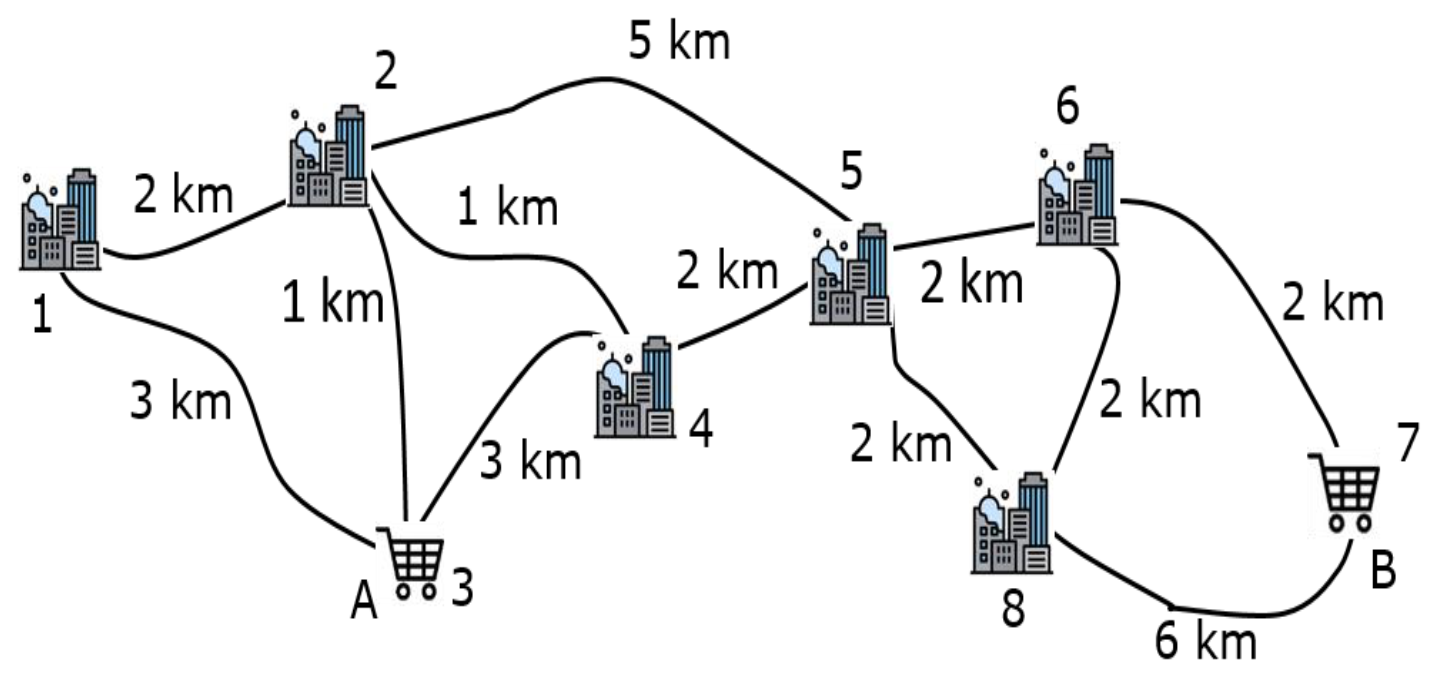
¿Cuál es el número mínimo de kilómetros que deberán recorrer los habitantes de las poblaciones para ir a un supermercado PrecioJusto?
Debido a unas obras de alcantarillado,las carreteras que unen la población 2 con la 5, y la población 4 con la 5 están en obras, lo que produce atascos monumentales ¿A qué supermercado (PrecioJusto A o PrecioJusto B) tendrán acceso los habitantes de los distintos pueblos si no quieren pasar por el tramo en obras?
Una vez terminadas las obras de alcantarillado y dado el estado en que han quedado parte de las carreteras, lo antiguo de otras, y la alta afluencia de veraneantes, los gerentes de los supermercados PrecioJusto A y B hablan con los ayuntamientos para que mejoren los accesos a estos centros. El ayuntamiento se queja de que el presupuesto va a ser muy alto, a lo que los supermercados replican que no es necesario que lo renueven todo, pero sí lo suficiente para que desde cualquier población se pueda llegar por una carretera en buen estado a cualquiera de ellos y que, en ese caso, colaborarán económicamente. Hacen hincapié en que, dado el gran número de habitantes de la población 4, esta debe estar unida al supermercado PrecioJusto A, con una buena carretera y, además, lo más corta posible. ¿Qué les recomendarías hacer? ¿Cuál sería el coste total del proyecto si este es proporcional a los kilómetros construidos entre las poblaciones?
El apartado a), donde buscamos caminos más cortos, lo resolvemos aplicando el algoritmo de Dijkstra, a los vértices 3 y 7, correspondientes a los supermercados. En el apartado b) es conveniente construir un nuevo grafo, eliminando las aristas correspondientes a las carreteras con atasco, y aplicar algoritmos de búsqueda como BFS o DFS. Por último, en el apartado c) aplicamos Dijkstra entre los vértices 4 y 3, para obtener el camino más corto entre la población 4 y el supermercado PrecioJusto A, y para garantizar que al aplicar el algoritmo de Kruskal se mantenga el camino obtenido, sustituimos el peso de sus aristas por 0, de manera que Kruskal las elegirá en primer lugar al calcular el árbol generador de mínimo coste.
A la hora de aplicar los algoritmos necesarios para resolver los problemas, utilizamos el software libre SWGraphs, lo que nos permite ser más eficientes y centrarnos en trabajar una correcta modelización de los problemas. En artículos [4], [5], [6], [7] y [8], o bien en el libro [9] se pueden consultar más ejemplos de este tipo.
Evaluación
La evaluación constituye el broche final de la docencia, siendo una de las etapas más importantes y, sobre todo, más delicada del proceso.
Desde nuestro punto de vista, la evaluación debe ser formativa, es decir, es importante que forme parte del proceso de aprendizaje y sea coherente con él. Por tanto, un cambio en la metodología conlleva necesariamente un cambio en el diseño de los sistemas de evaluación aplicados.
Proponemos, desde esta perspectiva, dos posibles escenarios:
- Opción 1: Examen con dos partes.
- Parte 1: Prueba escrita con cuestiones teóricas.
- Parte 2: Prueba práctica, a través de problemas de modelización con la ayuda de algún tipo de software.
- Opción 2: Examen y trabajo.
- Prueba escrita con cuestiones teóricas.
- Trabajo: Presentación de un problema original, que sintetice la aplicación de la teoría y los algoritmos estudiados.
En nuestra opinión, la segunda opción resulta la más interesante, aunque la cantidad de alumnos en el aula puede hacerla inviable para el profesor debido a la excesiva carga de trabajo que supone.
Conclusiones
La adaptación de la metodología y la evaluación de las asignaturas donde se imparte la teoría de grafos en la titulación de Ingeniería Informática de la ETSINF de la UPV, basada en la modelización matemática y la utilización de nuevas tecnologías, ha contribuido a mejorar el aprendizaje significativo en los alumnos, así como a favorecer la adquisición de las competencias propias del título, necesarias para formar profesionales cualificados.
Los resultados obtenidos en los cursos donde hemos implementado esta metodología de forma gradual, nos ha reafirmado en lo interesante que resulta un enfoque aplicado y más realista de las asignaturas para los estudiantes.
Referencias
[1] Wolfram. Página web <Wolfram: Computation Meets Knowledge> [Consulta: 16 de julio de 2022].
[2] Chamorro Molina, J. Solving With Graphs 2.0 (2014). Página web [Consulta: 16 de julio de 2022].
[3] Arnold, M., Millar, R. Learning the scientific «story»: a case study in the teaching and learning of elementary thermodynamics. Science Education, 80, 3, 249-281 (1996).
[4] Jordán, C., Burriel, J., Hérraiz, R. Un problema a resolver con los algoritmos de caminos más cortos, Modelling in science education and learning, 4, 21 (2011).
[5] Jordán, C., Sanabria-Codesal, E., Pérez Peñalver, M. J. Estrategias matemáticas en la ONU, Pensamiento matemático, Vol. II, 2, 55-66 (2012).
[6] Jordán, C., Sanabria-Codesal, E. Grafos hamiltonianos en el diseño de viajes, Modelling in science education and learning, 6, 2, (2013).
[7] Jordán, C., Murillo-Arcila, M., Torregrosa, J. R. The STEM Methodology and Graph Theory: Some Practical Examples. Mathematics, 9, 23 (2021).
[8] Cordero, A., Jordán C., Murillo-Arcila M., Sanabria-Codesal E. A Game for Learning How to Model in Graph Theory. Mathematics, 1, 1 (2022).
[9] Jordán, C., Murillo-Arcila, M., Seoane-Sepúlveda, J. B. Teoría de grafos y modelización. Problemas resueltos. Ed. Paraninfo, 2022. ISBN: 9788413679280.