Las Ecuaciones Diferenciales Ordinarias como instrumento para alcanzar los Objetivos de Desarrollo Sostenible
Resumen
Aunque los Objetivos de Desarrollo Sostenible (ODS) son una iniciativa internacional muy importante, encontramos que la desconocen gran parte de la población, y en concreto de los estudiantes de la Facultad de Ciencias Matemáticas de la Universitat de València.
Hemos introducido a estudiantes de segundo curso, del grado en matemáticas y del doble grado en física y matemáticas, en la iniciativa de los ODS mediante la asignatura “Ecuaciones Diferenciales Ordinarias” (EDO).
Poniendo de manifiesto la fuerte relación que tienen las EDO con los ODS, se quiere contextualizar la asignatura socialmente. Esto pretende que los/las estudiantes vean que, como futuros matemáticos, sus conocimientos y habilidades matemáticas pueden emplearse en la resolución de problemas reales de calado.
Palabras clave
EDO, ODS.
Abstract
Although the Sustainable Development Goals (SDG) is a very important international initiative, we find that a large part of the population, and specifically the students of the Mathematical Sciences Faculty of the Universitat de València, are unaware of it.
We have introduced second year students, of the degree in mathematics and of the double degree in physics and mathematics, in the SDG initiative through the subject “Ordinary Differential Equations” (ODE).
Highlighting the strong relationship that the ODE have with the SDG, we want to contextualize the subject socially. This is intended for students to see that, as future mathematicians, their mathematical knowledge and skills can be used in solving real world problems.
Keywords
ODE, SDG.
Introducción
Los Objetivos de Desarrollo Sostenible (ODS) son una iniciativa internacional con la intención de luchar contra el cambio climático y las desigualdades económicas y sociales mediante el consumo responsable de los recursos naturales y el uso y desarrollo de nuevas tecnologías, entre otros medios. Además, estos objetivos planteados deben alcanzarse antes del año 2030.
A pesar de la importancia del proyecto y su urgencia, buena parte de la población desconoce los ODS, en particular, el estudiantado de la Facultad de Ciencias Matemáticas de la Universitat de València.
Pensamos que no se trata el tema de los ODS en las asignaturas de matemáticas, aunque las matemáticas juegan un papel decisivo para alcanzar los objetivos, ya que sostienen a nivel técnico gran parte de las innovaciones tecnológicas y permiten analizar con fiabilidad y potencia datos de todo tipo. Cabe destacar esto porque nuestra sociedad está aumentando la producción de datos, los cuales conviene procesar y analizar.
En particular, las Ecuaciones Diferenciales Ordinarias (EDO) se utilizan para modelizar fenómenos de diversas procedencias. Por ejemplo, fenómenos naturales y sociales. Por tanto, se pueden utilizar para la optimización de recursos o para simular y predecir eventos. Las EDO pueden ayudar a lograr cada uno de los 17 ODS. En la Tabla 1 especificamos cómo se relaciona cada ODS con cada cita de la bibliografía.
Los autores de este trabajo hemos llevado a cabo en el curso 2021-2022 un proyecto de innovación educativa titulado “Conscienciar sobre els Objectius de Desenvolupament Sostenible mitjançant les Equacions Diferencials Ordinàries”, con el que se proponía introducir a los estudiantes de nuestra facultad en la iniciativa de los ODS mediante las asignaturas Ecuaciones Diferenciales Ordinarias del grado en matemáticas y del doble grado en física y matemáticas, en la Universitat de València.
Pensábamos que contextualizar la asignatura de esta forma motivaría al estudiantado, porque verían cómo ellos, como futuros matemáticos, pueden utilizar sus conocimientos y habilidades matemáticas para la resolución de problemas reales. Se pretendía que las/os estudiantes tomen conciencia de los ODS, que están ligados a problemas actuales de la sociedad, y motivarlos con esta perspectiva práctica y útil de la asignatura para facilitar el aprendizaje autónomo.
Metodología
Se han realizado diapositivas en las que se relaciona las EDO con los ODS [M2] y se ha realizado un vídeo explicativo [M1]. Se han elaborado y distribuido encuestas a las/os estudiantes para analizar el impacto de esta propuesta educativa [M3].
Los ODS se han trabajado, principalmente, en las sesiones de seminario. Las sesiones de teoría son muy abstractas en esta asignatura, y no da pie a hablar de problemas reales. Las sesiones de prácticas, a su vez, pretenden que los estudiantes se familiaricen con los conceptos de teoría y los trabajen. Es por tanto en las sesiones de seminario, que están presentes desde el comienzo del cuatrimestre hasta el final, son una buena oportunidad para que los estudiantes salgan de la abstracción del temario, presentándoles problemas de la sociedad que pueden resolver con lo que están aprendiendo en este curso.
Acciones realizadas
En la introducción de la asignatura, en la primera semana de clase, los profesores de teoría hablaron sobre los ODS y plantearon el contenido de la asignatura como una manera de afrontar los ODS. Con esta acción se pretendía motivar a los estudiantes a ver el contenido de la asignatura como algo útil. Antes de la primera sesión de la asignatura, se facilitó un cuestionario online [M3→Encuesta 1] en el que valoraron lo útil que les parece las matemáticas en la resolución de problemas de la sociedad.
Se presentó cada uno de los 17 ODS, mediante un vídeo explicativo [M1], dando la relación que tienen con las EDO, para el cual se elaboraron unas diapositivas [M2]. El vídeo se mostró a los estudiantes antes de la primera sesión de seminarios, en la que tuvieron que trabajar las EDO orientadas a los ODS. El vídeo sigue el esquema de la Tabla 1:
| ODS | Uso de las EDO |
|---|---|
| ODS 1, 8 (Fin de la pobreza, Trabajo decente y crecimiento económico) | Modelado económico [1] |
| ODS 2, 4 (Hambre cero, Educación de calidad) | Dinámica de poblaciones y recursos [2] |
| ODS 3 (Salud y bienestar) | Medicina [3] |
| ODS 5, 10 (Igualdad de género, Reducción de las desigualdades) | Modelización de fenómenos sociales [4] |
| ODS 6 (Agua limpia y saneamiento) | Optimización del tratamiento de aguas residuales [5] |
| ODS 7 (Energía asequible y no-contaminante) | Modelizar la producción y demanda de energía [6] |
| ODS 9 (Industria, innovación e infraestructuras) | Industria [7] |
| ODS 11 (Ciudades y comunidades sostenibles) | Modelado del tráfico [8] |
| ODS 12 (Producción y consumo responsable) | Economía circular [9] |
| ODS 13 (Cambio climático) | Simulación climática [10] |
| ODS 14, 15 (Vida submarina, Vida de ecosistemas terrestres) | Simulación de ecosistemas [11] |
| ODS 16, 17 (Paz, justicia e instituciones sólidas, Alianzas para conseguir los objetivos) | Descripción de sistemas políticos [12] |
Con esta acción se pretende que los estudiantes tomen conciencia de cuál es la finalidad del proyecto de los ODS, consolidando lo tratado en la primera semana de clases de Teoría. Antes de la primera sesión de seminarios, facilitamos un cuestionario en el que pudieron valorar lo útil que les parece las EDO, en particular, con la misma finalidad [M3→Encuesta 2]. Así pudimos comparar el efecto de esa presentación del contenido.
En la Encuesta 1 se les preguntó si conocían este proyecto internacional. En la Encuesta 2 se les preguntó lo importante que consideran los ODS en el futuro de la sociedad y cuánta amplitud/transversalidad del proyecto consideran que tiene. También sobre cuánta relación piensan que tienen con las matemáticas.
Se plantearon tareas en las que trabajar con EDOs con orientación a los ODS, durante las sesiones de Seminario:
- Trabajo sobre modelos poblacionales (Sesiones de Seminario 1 y 2).
- Trabajo sobre modelos de propagación de enfermedades infecciosas (Sesiones de Seminario 5).
Se pretendió que los alumnos trabajasen los contenidos del curso con un ejemplo cercano a la realidad, con el fin de que aprendan a aplicar los resultados teóricos a la práctica. Las encuestas 2 y 3 sirvieron para obtener su impresión sobre la utilidad de la asignatura en su futuro matemático y laboral. La encuesta 3 [M3→Encuesta 3] fue cumplimentada al final de curso.
Resultados
Se han pasado tres encuestas a los estudiantes que pretendían medir el impacto que tiene la contextualización de la asignatura en el concepto que los estudiantes tienen de la asignatura y de su utilidad práctica. También sobre si conocen a los ODS y sobre la utilidad de las matemáticas y, en particular, de las EDO en problemas reales y para lograr los ODS.
A continuación, se presentan los resultados más relevantes de las encuestas. Para conocer todos los resultados, puede consultarse los archivos en [M3]. Cada pregunta tiene como respuesta un número entero del 1 al 5. A lo largo de esta sección, mostraremos un seguido de gráficas mostrando la frecuencia relativa de cada respuesta.
De un total de 136 matriculados en la asignatura (que corresponden a dos grupos del Grado en Matemáticas y a un grupo del Doble Grado en Física y Matemáticas), se han obtenido un total de 92, 59 y 60 respuestas, en cada una de las tres encuestas. Se aprecia una severa reducción de la tasa de participación.
En una encuesta inicial, antes de introducir los ODS, se les pregunta si los conocen y también por la utilidad práctica de su titulación. Hemos encontrado que una minoría conocen a los ODS y que la utilidad que consideran de las matemáticas para resolver problemas reales es elevada (ver Figura 1 y Figura 2).
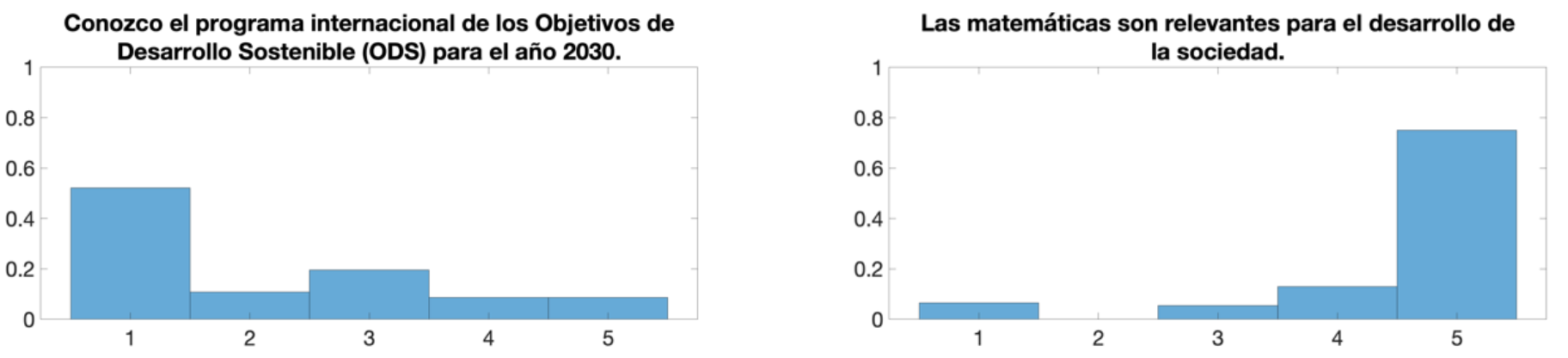
Del hecho que los estudiantes ya tenían una idea útil de las matemáticas, se deduce que las acciones formativas de este proyecto no pueden tener un impacto significativo en este sentido. Sería interesante ver las consecuencias de estas acciones en estudiantes no-matemáticos.
Un hecho destacable es que consideran que las matemáticas son relevantes para la resolución de problemas reales, pero no creen que lo sean tanto en su futuro laboral (ver Figura 2). Nosotros pensamos que su futuro laboral y la resolución de problemas reales están ligados y nos preguntamos qué explica esta (modesta) diferencia.
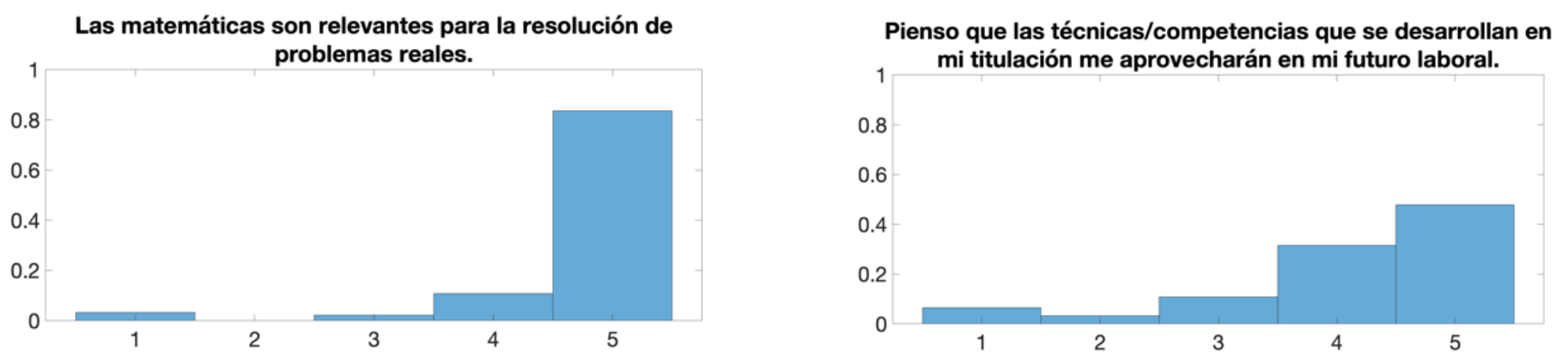
Encontramos resultados muy similares en las preguntas “Pienso que el contenido/temario que se imparte en mi titulación me aprovechará en mi futuro laboral” y “Pienso que las técnicas/competencias que se desarrollan en mi titulación me aprovechará en mi futuro laboral”. Como era de esperar, es algo superior cuando se pregunta por las competencias, ya que es uno de los argumentos clásicos cuando se defiende los estudios en matemáticas, pero sorprende un poco (y nos alegra) que estudiantes de segundo curso consideren igualmente útil su contenido, a pesar de ser tan específico y abstracto.
En la segunda encuesta, que se realizó dos semanas después de la primera encuesta y el primer seminario, ya habiéndolos introducido los ODS, casi todos afirmaban conocer a los ODS (como es de esperar), pero además mejoraron las respuestas de la pregunta “Las matemáticas son relevantes para superar las desigualdades sociales” (ver Figura 3).
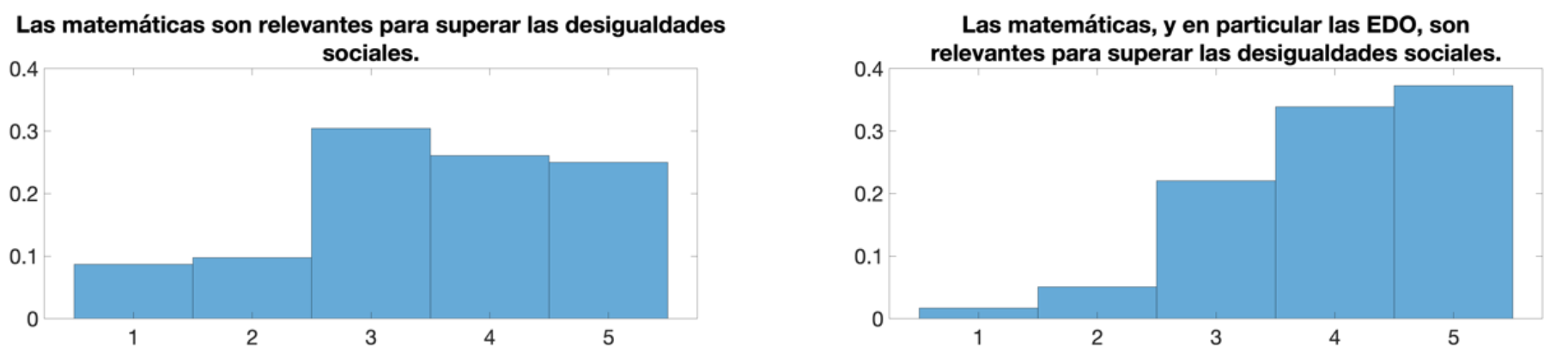
De la primera y segunda encuesta se obtiene que los estudiantes piensan que las matemáticas son útiles, pero las Ecuaciones Diferenciales Ordinarias lo son algo menos que las matemáticas (ver Figura 4). Es razonable siendo que una contiene a la otra. En este sentido, las acciones realizadas han tenido poco efecto, ya que los estudiantes tenían previamente una alta consideración de las matemáticas. Sería interesante ver las consecuencias de estas acciones en estudiantes no-matemáticos.
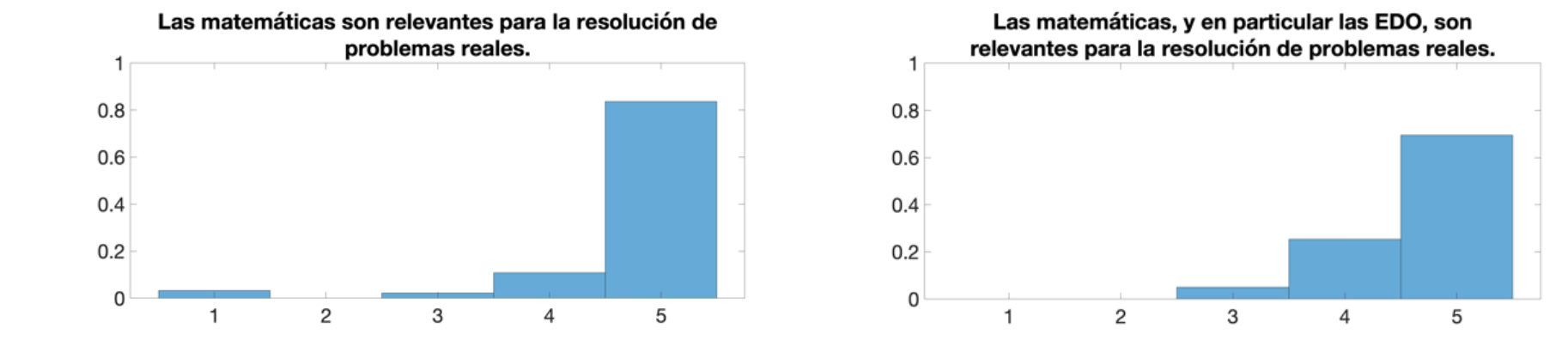
Detectamos en el doble grado Física-Matemáticas, que se realizó en el primer cuatrimestre del curso, que pocos estudiantes visualizaban el vídeo antes de llenar la segunda encuesta, que conducía a respuestas numéricamente más bajas en la encuesta. Tras incluir la pregunta trivial “¿Has visto el siguiente vídeo? https://youtu.be/RVnykFXqccY” al principio del cuestionario en el segundo cuatrimestre para el grado en Matemáticas, encontraremos que las respuestas mejoraron considerablemente. Esto pone de relevancia la importancia de diseñar estrategias de control para que los estudiantes cumplan las instrucciones del profesorado.
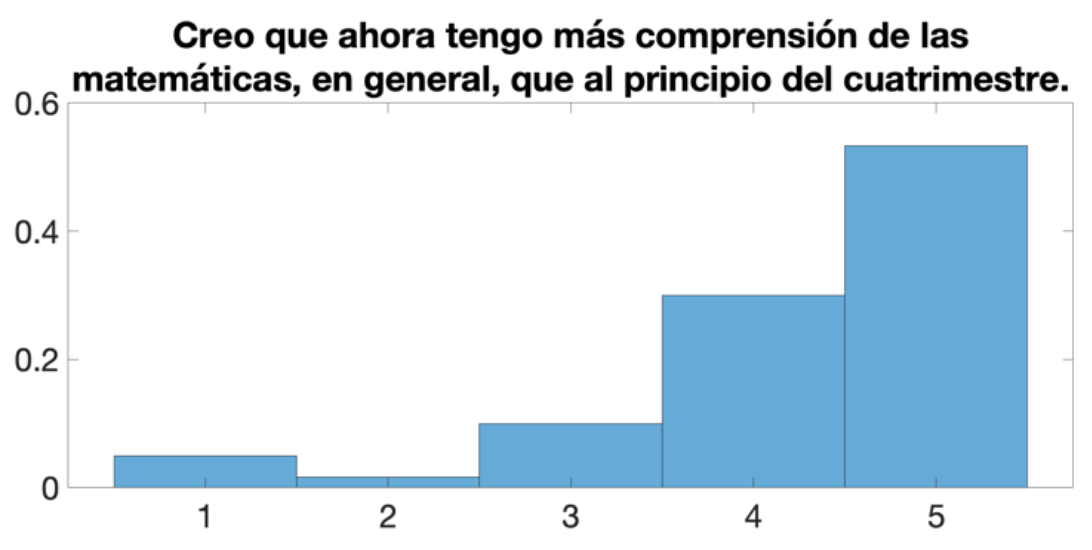
De la tercera encuesta [M3] se reafirma su útil percepción de las matemáticas, y en particular de las EDO, en el futuro del estudiantado. Nos llena de satisfacción saber que las respuestas a “Creo que ahora tengo más comprensión de las matemáticas, en general, que al principio del cuatrimestre han sido muy elevadas” son tan positivas (ver Figura 5).
Conclusiones
Pensábamos que mostrar la relación entre los ODS y las EDO haría que la asignatura se contextualice en el panorama social. De esta forma, el estudiante podría percibir el temario como algo útil y necesario para que en el futuro ella/él pueda contribuir como parte trabajadora de la sociedad. Esto podría transformarse en motivación y mejorar los resultados académicos. Sin embargo, hemos visto en las encuestas que esta percepción es ya bastante alta, y por tanto el impacto puede haber sido bajo en este sentido.
Esto lleva a pensar que el impacto puede ser mucho mayor si estas acciones se aplicasen a estudiantes con una menor percepción de la utilidad de las matemáticas a priori, como bien podría ser en otras titulaciones. Sería interesante comprobarlo en un futuro proyecto de innovación educativa. Sin duda las acciones han servido para que los estudiantes conozcan a los ODS. La parte de divulgación de los ODS (vídeo y diapositivas) es accesible incluso para un perfil de estudiantes no-matemáticos (incluso no-científico), por lo que podría difundirse a otros estudiantes universitarios o no-universitarios. Sería especialmente transferible a otras asignaturas de matemáticas en las que se estudian EDOs (como en ingenierías y en otras ciencias básicas). En esas situaciones, valdría para contextualizar la unidad didáctica de las EDO en el contexto social.
También es transferible a asignaturas no-matemáticas la siguiente conclusión obtenida de las encuestas: Se ha puesto de manifiesto que relacionar la asignatura con los ODS hace que la asignatura se contextualice en el panorama social, sobre todo en la lucha contra las desigualdades. De esta forma, el estudiante percibe el temario como algo útil y necesario para que en el futuro él/ella pueda contribuir como parte trabajadora de la sociedad. Esto podría transformarse en motivación y mejorar los resultados académicos, especialmente cuando el temario no tiene una alta percepción inicial por parte de los estudiantes.
Agradecimientos
Los autores agradecen el soporte de la Universitat de València dado a través del proyecto de innovación educativa UV-SFPIE_PID-1639406.
Material
[M1] Vídeo introductorio
[M2] Entrada del blog con las diapositivas
[M3] Material de las sesiones de seminario, encuestas y resultados de las encuestas
Referencias
[1] C.-F. Lee i J. Shi, «Application of Alternative ODE in Finance and Economics Research,» de Handbook of Quantitative Finance and Risk Management, Springer US, 2010, pp. 1293-1300.
[2] M. Austin, D. Boelkins i S. Schlicker, «Population Growth and the Logistic Equation,» 2020. [En línia]. Available.
[3] P. Deuflhard, «Differential equations in technology and medicine: Computational concepts, adaptive algorithms, and virtual labs,» de Computational Mathematics Driven by Industrial Problems: Lectures given at the 1st Session of the Centro Internazionale Matematico Estivo (C.I.M.E.) held in Martina Franca, Italy, June 21- -27, 1999, Berlin, Springer Berlin Heidelberg, 2000, pp. 69-125.
[4] L. Ó. Náraigh, «A differential-equation-based model of the glass ceiling in career progression,» The Journal of Mathematical Sociology, vol. 44, núm. 1, pp. 42-64, 2020.
[5] M. Nova i P. Horvat, «Mathematical modelling and optimisation of a waste water treatment plant by combined oxygen electrode and biological waste water treatment model,» Applied Mathematical Modelling, vol. 36, núm. 8, pp. 3813- 3825, 2012.
[6] L. Zjavka i V. Snásel, «Power Output Models of Ordinary Differential Equations by Polynomial and Recurrent Neural Networks,» de Innovations in Bio-inspired Computing and Applications, Springer International Publishing, 2014, pp. 1-11.
[7] E. Momoniat, T. G. Myers, M. Banda i J. Charpin, «Differential Equations with Applications to Industry,» International Journal of Differential Equations, vol. 2012, p. 491874, 2012.
[8] M. Herty, A. Klar i A. Singh, «An ODE traffic network model,» Journal of Computational and Applied Mathematics, vol. 203, núm. 2, pp. 419-436, 2007.
[9] F. Charnley, D. Tiwari, W. Hutabarat, M. Moreno, O. Okorie i A. Tiwari, «Simulation to enable a data-driven circular economy,» Sustainability, vol. 11, núm. 12, p. 3379, 2019.
[10] J. F. N. Dunmyre, T. Bogart, C. Rasmussen i K. Keene, «Climate Change in a Differential Equations Course: Using Bifurcation Diagrams to Explore Small Changes with Big Effects,» CODEE Journal, vol. 12, núm. 1, p. 1, 2019.
[11] S. Busenberg, Differential Equations and Applications in Ecology, Epidemics, and Population Problems, Elsevier, 2012.
[12] A. K. Misra, «A simple mathematical model for the spread of two political parties,» Nonlinear Analysis: Modelling and Control, vol. 17, núm. 3, pp. 343-354, 2012.