Álgebra Lineal y Geometría I : El pódcast
Resumen
En este estudio presentamos una experiencia de innovación educativa llevada a cabo en la asignatura de Álgebra Lineal y Geometría I del grado en Matemáticas. El alumnado formó grupos para realizar entrevistas en formato audio a personas que explicaban cómo aplicaban en su trabajo los conceptos estudiados en la asignatura. Los resultados fueron utilizados para crear un programa de pódcasts en línea. Al finalizar se llevó a cabo una encuesta para recoger la opinión del estudiantado sobre la actividad. Evaluamos la capacidad de la propuesta para involucrar al alumnado en el aprendizaje, contextualizar los conocimientos y fomentar habilidades interpersonales. Se presentan las conclusiones sobre esta experiencia y posibles mejoras para ediciones futuras del proyecto.
Palabras clave
Pódcast, Educación Superior, Matemáticas.
Abstract
In this study we present an educational innovation experience carried out in the subject of Linear Algebra and Geometry I in the Mathematics degree. Students formed groups to conduct audio interviews with people who explained how they applied to their work the concepts studied in the subject. The results were used to create an online podcast program. At the end, a survey was conducted to collect students’ opinions on the activity. We evaluated the proposal’s ability to involve students in learning, contextualize knowledge, and promote interpersonal skills. We present the conclusions about this experience and possible improvements for future editions of the project.
Keywords
Podcast, Higher education, Mathematics.
Introducción
La tecnología ha revolucionado la forma en que el profesorado se relaciona con el estudiantado, brindando nuevas oportunidades para el aprendizaje en entornos virtuales y a través de la educación en línea. En particular, los pódcasts han destacado como una herramienta eficaz y flexible para la enseñanza y el aprendizaje en diversos campos [5, 6, 7], incluyendo las matemáticas [2]. Estas investigaciones concluyen que los pódcast tienen efectos positivos en el compromiso, la satisfacción y los resultados de aprendizaje del estudiantado.
En este artículo, se presenta una experiencia innovadora en la asignatura de Álgebra Lineal y Geometría I del grado en Matemáticas, donde se utilizó el pódcast como una forma de contextualizar los resultados y promover habilidades interpersonales. El objetivo principal del trabajo es analizar las características de este formato y discutir su capacidad para contextualizar los resultados en el ámbito de las matemáticas, así como su potencial para fomentar habilidades interpersonales y promover un aprendizaje significativo.
En esta experiencia, el estudiantado llevó a cabo entrevistas en formato de audio a profesionales que aplican los conceptos estudiados en la asignatura en su trabajo. Estas entrevistas se utilizaron para crear un programa de pódcasts en línea, donde el alumnado pudo compartir sus hallazgos y reflexiones con el resto de la clase y con una audiencia más amplia. Al finalizar la actividad, se recopiló la opinión del estudiantado a través de una encuesta para evaluar el impacto de la propuesta en su aprendizaje y desarrollo de habilidades. En este artículo, se presentan los resultados de esta experiencia, destacando los aspectos positivos y los desafíos encontrados. Además, se discuten posibles mejoras y recomendaciones para futuras ediciones de este proyecto.
Contexto
La asignatura de Álgebra Lineal y Geometría I tiene carácter básico en el Grado en Matemáticas impartido en la Universitat de València y se cursa durante los dos cuatrimestres del primer curso, conformando una asignatura de 12 ECTS dentro de la materia “Matemáticas” dentro del módulo de asignaturas denominadas de “Formación Básica”.
Los objetivos generales de la asignatura de Álgebra Lineal y Geometría I son el desarrollo de los conceptos de espacio vectorial y aplicación lineal entre espacios vectoriales, con especial atención a su representación matricial, así como los conceptos básicos de métrica en espacios vectoriales euclidianos y su aplicación en espacios afines. Cabe destacar que la asignatura de Álgebra Lineal y Geometría I es una asignatura transversal que servirá de ejemplo constante sobre el que volver en relación a asignaturas de cursos superiores, bien sea por sus métodos, conceptos o razonamientos.
En esta asignatura es especialmente importante reflexionar acerca del uso de la multiplicación matricial, ya sea como ejemplo de transformación de ciertas estructuras afines o lineales, su interpretación geométrica, descrita principalmente mediante el uso de vectores y valores propios, su interacción con la métrica definida en algún espacio vectorial euclidiano o afín euclidiano o con la descripción de representaciones matriciales de isometrías (giros y reflexiones principalmente) o translaciones, homotecias o combinaciones de las anteriores. Se pretende evitar la concepción de la matriz como espacio contenedor y reafirmarla como elemento transformador. Además, se insiste en la capacidad de elección que se tiene para representar estas acciones, incidiendo especialmente en las bondades de una representación diagonal.
Desde el Grado en Matemáticas estas nociones pueden sufrir el problema de encontrarse descontextualizadas cuando, al contrario, todos los conceptos trabajados en la asignatura tienen una ingente cantidad de aplicaciones en contextos variados y transversales. Desde esta asignatura se pueden trabajar los conceptos de cadenas de Markov, análisis de grafos, coeficientes de correlación, criptografía, interpolación, predicciones a largo plazo, ecuaciones en diferencias, sistemas de ecuaciones diferenciales lineales, análisis de redes, mínimos cuadrados lineales, modelos poblacionales, métodos de la potencia para la aproximación del valor propio dominante, aspectos de programación lineal, gráficos por ordenador, teoría de códigos, descomposición espectral, análisis de componentes principales, teoría de campos vectoriales, sistemas dinámicos discretos y continuos, soluciones iterativas, tratamiento de imágenes, flujos de tráfico o polinomios ortogonales, entre algunas de sus aplicaciones.
Descripción general del alumnado
El alumnado inscrito en la asignatura proviene, principalmente, de bachillerato científico y accede al grado mediante las pruebas de acceso a la Universidad. Son personas que sienten especial inclinación hacia el razonamiento abstracto, con afición y destreza para resolver problemas tanto de naturaleza lógica como calculista, que demuestran capacidad de síntesis, modelización, abstracción y razonamiento lógico, así como hábito de trabajo intelectual y dedicación al estudio. No obstante, suelen encontrarse con dificultades para la adaptación al grado, principalmente por problemas en su expresión matemática, en el desarrollo de razonamientos y demostraciones y en la adecuación del hábito de estudio y la carga de trabajo al contexto universitario.
Es importante tener en cuenta el bagaje sobre sistemas de ecuaciones lineales que el alumnado trae consigo desde bachillerato y que permite tener un anclaje desde el que poder avanzar la asignatura. La familiaridad con las soluciones de un sistema de ecuaciones lineal y los métodos para su obtención, así como la interpretación geométrica de estas soluciones como variedades afines y su representación matricial son fundamentales para el desarrollo de la asignatura. También ayudan las nociones básicas de trigonometría y de uso de determinantes que el alumnado haya podido obtener en los últimos cursos de instituto. Pero, sobre todo, ayudará el hecho de que el alumnado haya desarrollado con anterioridad un razonamiento crítico, más próximo a la actividad matemática.
Actividad propuesta
Se propuso una actividad en grupo de un máximo de 4 personas. El grupo debía identificar una persona de su entorno que utilizara algunos de los resultados vistos en clase. El grupo debía realizar previamente el guión de una entrevista donde se remarcara la relación de esta persona con las matemáticas y donde se identificaran los conceptos y resultados trabajados en el aula. La entrevista debía ser breve, con una duración total de entre 5 y 10 minutos. El grupo únicamente debía entregar el fichero de audio por correo electrónico. Las grabaciones se compartían con el resto de la clase mediante el Aula Virtual y eran puestas a libre disposición del público en formato pódcast.
La actividad se propuso como actividad evaluable para el seminario del segundo cuatrimestre de la asignatura de Álgebra Lineal y Geometría del curso 21/22, dentro del Grado en Matemáticas. Al realizarla en el segundo cuatrimestre, el alumnado ya tenía una experiencia previa sobre los contenidos de la asignatura. Esta actividad formaba parte del proyecto de innovación docente “Desarrollo de competencias transversales a través de las Matemáticas. Versión 2.0” de la Facultad de Ciencias Matemáticas.
Objetivo
El objetivo principal de la actividad es contextualizar las definiciones, proposiciones y conceptos vistos en clase e identificar sus aplicaciones. Otro objetivo de esta actividad es caracterizar y diseñar secuencias de aprendizaje que favorecieran la adquisición de competencias transversales para el alumnado, centradas principalmente en la comunicación oral y el desarrollo de habilidades interpersonales. Estos objetivos están en consonancia con los resultados del aprendizaje y las habilidades sociales que se espera obtener al cursar esta asignatura [4].
Preparación
Se puso a disposición del alumnado en el Aula Virtual un documento informativo [3] con el objetivo de contextualizar la actividad, describir la propuesta y los objetivos y ayudar a la preparación de la actividad.
Se pidió al alumnado que buscara una persona que pudiera hacer servir algunas de las técnicas o nociones trabajadas en clase. Se les instó a pensar en el entorno familiar, en el profesorado de sus institutos, en compañeros o compañeras de otras titulaciones o en profesionales de todas las ramas del conocimiento. También se les instó a dejar de lado los prejuicios sobre las personas que pudieran utilizar el álgebra lineal en su trabajo.
Una vez identificada la persona a entrevistar, se les pidió identificar alguna de las nociones que esta persona pudiera utilizar en su campo de especialización, así como el significado específico que pudiera darle a esa noción en su contexto, esto es, qué nociones utiliza y qué significados les da. También se pidió al alumnado que investigara por su cuenta sobre el tema concreto y se preguntase cómo relacionarlo con los contenidos vistos en clase.
Se pidió a los grupos que preparasen la entrevista antes de grabarla, que redactasen un guión previo de lo que iban a preguntar y que trabajaran este guión con la persona entrevistada antes de iniciar la grabación. El público al que se tendría que dirigir la entrevista era a los compañeros y compañeras de la asignatura. Para la grabación se instó a la utilización del móvil y se animó a que realizasen el montaje que considerasen oportuno.
Se pidió también coherencia y cohesión en el desarrollo de la entrevista. Se pidió que la entrevista empezara con la presentación de las personas integrantes del grupo, la introducción adecuada de la persona entrevistada, incidiendo en la relación que tuviera esta persona con las matemáticas. Una vez realizada la presentación se pidió que se introdujese el tema o el concepto matemático a tratar en la entrevista y que ayudasen a la persona entrevistada a buscar la conexión entre su campo de especialización y los conceptos trabajados en clase, así como con otros temas relacionados. Se pidió concluir la entrevista con una pequeña reflexión sobre los temas tratados y su relación con los conocimientos vistos en clase.
Evaluación
La actividad se evaluó dentro del apartado de seminario de la asignatura, que representa un 10 % de la nota final. Se puso a disposición del alumnado la rúbrica recogida en la Tabla 1 para identificar los aspectos fundamentales de la entrevista y ayudar a la evaluación posterior.
| Presentación del grupo | Hasta 1 punto |
| Registro lingüístico | Hasta 1.5 puntos |
| Introducción de la persona entrevistada | Hasta 1.5 puntos |
| Contenido de las preguntas | Hasta 2 puntos |
| Relación con los temas trabajados en clase | Hasta 2 puntos |
| Conclusiones y reflexión del grupo | Hasta 2 puntos |
Al acabar el cuatrimestre se pidió al alumnado que realizaran una encuesta para valorar la actividad. Los resultados de esta encuesta constituyen la fuente principal que se ha utilizado para el desarrollo del presente trabajo.
Resultados
Se presentaron 15 trabajos, que se pusieron a disposición del alumnado en el Aula Virtual y en dos plataformas de audio en línea, Ivoox y Spotify [1]. En las plataformas se detalló información sobre el proyecto y se utilizó un logo común para el contenido o la fotografía de las personas entrevistadas, según la disponibilidad.
Destacamos los siguientes detalles en relación a las entrevistas. De las 15 entrevistas, 13 (87 %) fueron realizadas a hombres y 2 (13 %) a mujeres. En relación a la profesión de las personas entrevistadas, 4 (26 %) eran docentes de secundaria, 3 (20 %) eran docentes universitarios, 3 (20 %) eran divulgadores, 3 (20 %) eran ingenieros, 1 (7 %) era físico y 1 (7 %) era economista. En relación al idioma utilizado en las entrevistas, 11 (73 %) fueron realizadas en catalán, 3 (20 %) en español y 1 (7 %) en inglés. La media de duración de los episodios fue de 10 minutos, con una desviación estándar de 3 minutos y 40 segundos.
La nota media del estudiantado en esta actividad fue de un 7.7 sobre 10. Se presenta en la Tabla 2 el detalle de la nota media en cada apartado de la rúbrica.
| Presentación del grupo | 0.9 puntos | (sobre 1) |
| Registro lingüístico | 1.3 puntos | (sobre 1.5) |
| Introducción de la persona entrevistada | 1.2 puntos | (sobre 1.5) |
| Contenido de las preguntas | 1.5 puntos | (sobre 2) |
| Relación con los temas trabajados en clase | 1.7 puntos | (sobre 2) |
| Conclusiones y reflexión del grupo | 1.1 puntos | (sobre 2) |
Además de estos aspectos, es importante destacar otros hallazgos no previstos con anterioridad. Se ha observado una variabilidad significativa en el contenido de las entrevistas realizadas. La mayoría de las entrevistas reflejan una comprensión sólida de los conceptos trabajados en clase, mostrando aplicaciones de vectores y valores propios, de la representación diagonal de matrices o cuestiones de ortogonalidad y distancias, mientras que otras se centran en temas más generales relacionados con la importancia de las matemáticas en la sociedad o su aplicabilidad en un sentido abstracto. Estas entrevistas no abordan cuestiones concretas de la asignatura, lo cual era uno de los objetivos de la actividad.
Encuesta
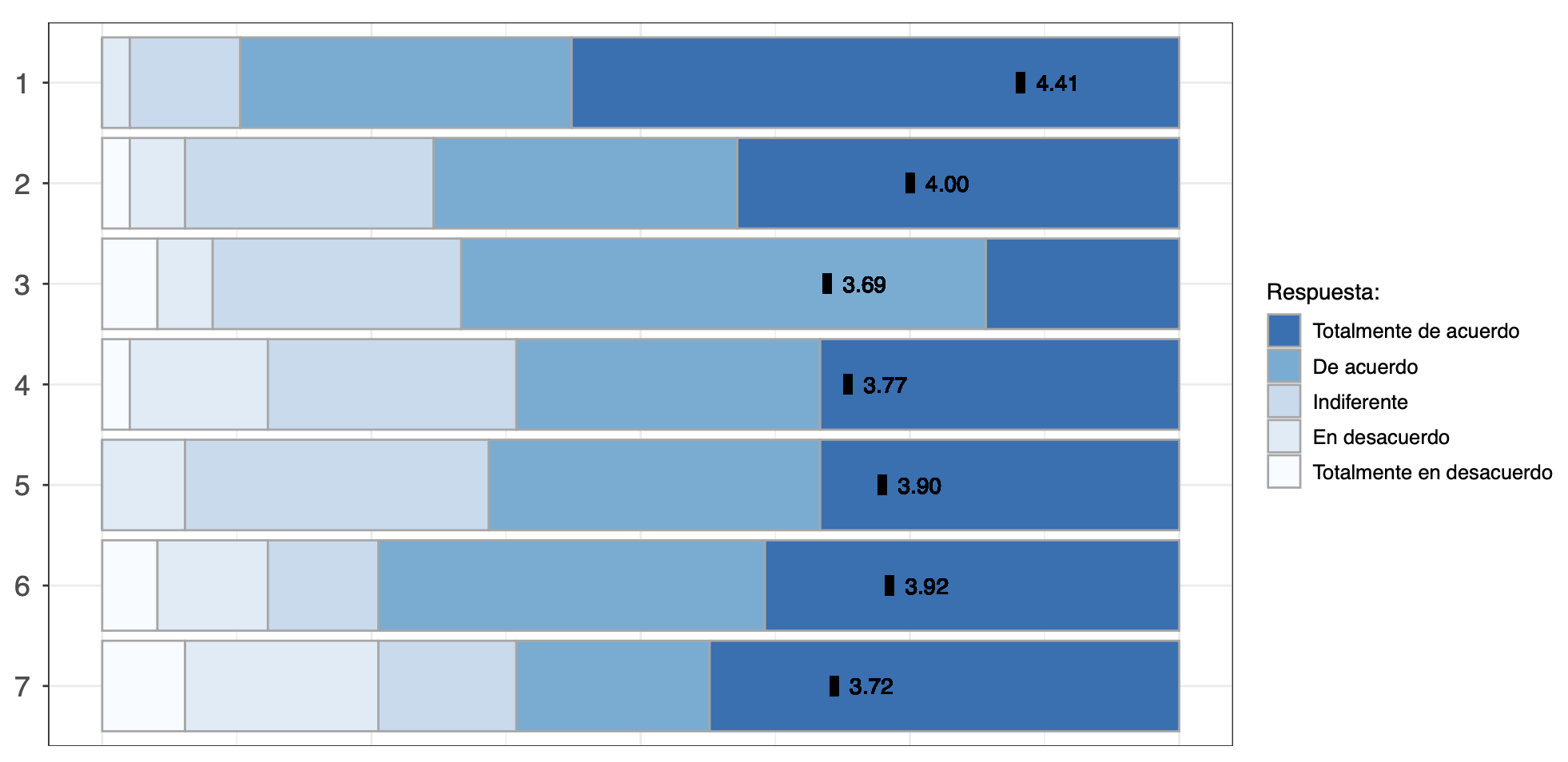
Al acabar el semestre se pidió al alumnado que contestase una encuesta en el Aula Virtual que recogía los apartados detallados en la Tabla 3. Se pidió evaluar los campos mediante las siguientes etiquetas (1) Totalmente en desacuerdo, (2) En desacuerdo, (3) Indiferente, (4) De acuerdo, (5) Totalmente de acuerdo. De las 59 personas matriculadas en el grupo, contestaron a la encuesta 39 (66 %). Se recogen los resultados en la Figura 1.
Valoración
Los resultados de la encuesta reflejan una evaluación generalmente positiva de la experiencia de uso de los pódcasts como herramienta de contextualización en la asignatura de Álgebra Lineal y Geometría I. El estudiantado ha valorado la claridad de la descripción de la actividad, con una puntuación media de 4.41, la utilidad de la rúbrica de evaluación, aproximadamente el 70 % de ellos estando de acuerdo o totalmente de acuerdo, la capacidad de la actividad para contextualizar contenidos, con una puntuación media de 3.77, y trabajar habilidades interpersonales (puntuación media de 3.90), así como su satisfacción general con la propuesta, 62 % de ellos estando de acuerdo o totalmente de acuerdo con este ítem.
| 1. La descripción de la actividad ha sido clara. |
| 2. La rúbrica de evaluación me ha sido de utilidad. |
| 3. La actividad propuesta me ha comportado poca carga de trabajo. |
| 4. La actividad me ha servido para contextualizar los contenidos. |
| 5. La actividad me ha servido para trabajar habilidades interpersonales. |
| 6. La actividad propuesta me ha gustado. |
| 7. Prefiero este tipo de actividades para los seminarios de la asignatura. |
Por otra parte, valoramos positivamente la experiencia desde el punto de vista del profesorado, pues esta actividad no ha generado una carga excesiva de trabajo y el formato utilizado ha permitido realizar una corrección eficiente y entretenida, en un entorno menos formal y estático. También se ha percibido que trabajar en equipo y escuchar las entrevistas de los compañeros ha fortalecido la interacción y la colaboración entre el alumnado, creando un ambiente más positivo y enriquecedor en la asignatura.
Conclusiones
En conclusión, la experiencia de uso de pódcasts como herramienta de contextualización de resultados en la asignatura de Álgebra Lineal y Geometría I ha demostrado ser beneficiosa tanto para el alumnado como para el profesorado. Los pódcasts han brindado al alumnado la oportunidad de aplicar los conocimientos adquiridos en situaciones reales, a través de entrevistas a profesionales que utilizan esos conceptos en su trabajo diario.
Esta experiencia ha fomentado el compromiso y la participación activa del alumnado, al permitirles compartir sus hallazgos con sus compañeros y con una audiencia más amplia a través de las plataformas en línea. Además, el uso de pódcasts ha facilitado el acceso flexible al contenido, lo que ha permitido al alumnado revisar y profundizar en los temas de una manera más conveniente y autónoma. Además de la contextualización de resultados, se ha observado que los pódcasts han contribuido al desarrollo de habilidades interpersonales, como la capacidad de comunicación y la colaboración en grupo. El estudiantado ha tenido la oportunidad de interactuar con profesionales y de compartir sus propias ideas y reflexiones.
Si bien esta experiencia ha sido exitosa, también se han identificado áreas de mejora. Una de ellas es la necesidad de considerar la diversidad en las personas entrevistadas, evitando cualquier tipo de sesgo, incluyendo aquellos relacionados con cuestiones de género. Es fundamental asegurar una representación equitativa de distintas voces y perspectivas en los contenidos de los pódcasts, para fomentar un ambiente inclusivo y enriquecedor. Además, es imprescindible una planificación y coordinación adecuadas para garantizar la participación activa de todo el alumnado y para que realicen entrevistas significativas y de calidad. Asimismo, se deben establecer pautas claras que proporcionen orientación adicional al alumnado para asegurar que el contenido de las entrevistas se enfoque en los conceptos específicos estudiados en la asignatura, asegurando que el contenido generado cumpla con los estándares académicos.
En definitiva, el uso de pódcasts en la asignatura de Álgebra Lineal y Geometría I ha enriquecido el proceso de aprendizaje al brindar una experiencia práctica y significativa. Esta experiencia ha destacado la importancia de integrar herramientas tecnológicas en el currículo de matemáticas para promover un aprendizaje activo, el desarrollo de habilidades y la contextualización de resultados. Se recomienda seguir explorando y promoviendo este tipo de experiencias en la educación matemática, en busca de una formación más enriquecedora y adaptada a las necesidades del estudiantado.
Agradecimientos
Agradecemos la labor del equipo editorial de las Terceras Jornadas de Innovación Docente en Matemáticas en Educación Superior de la Universitat de València, así como la revisión del presente trabajo por las personas encargadas.
Referencias
[1] Àlgebra Lineal i Geometria I - El podcast. Ivoox, Spotify (2022).
[2] Bergqvist, T. Podcasting mathematics. The International Journal for Techno- logy in Mathematics Education, 20 (4), 147 (2013).
[3] Cosme Llópez, E. Descripció de l’activitat, Àlgebra Lineal i Geometria I - El podcast. Enlace al documento, Visitado: 2023-10-18, (2021).
[4] Crespo García, R. Memoria de verificación del título oficial de grado: Graduado/a en Matemáticas. Enlace al documento, Visitado: 2023-06-05, (2010).
[5] Evans, C. The effectiveness of m-learning in the form of podcast revision lectures in higher education. Computers & education, 50 (2), 491–498 (2008).
[6] McGarr, O. A review of podcasting in higher education: Its influence on the traditional lecture. Australasian journal of educational technology, 25 (3), (2009).
[7] Merhi, M. I Factors influencing higher education students to adopt podcast: An empirical study. Computers & Education, 83, 32–43 (2015).