Estrategias inclusivas para la visualización de contenido matemático tridimensional
Resumen
El uso de herramientas tecnológicas en la enseñanza de los conceptos de geometría puede ser una estrategia que favorezca el diseño de propuestas inclusivas en la que se prevengan posibles dificultades. Es por ello que el objetivo de esta comunicación es el de presentar recursos tecnológicos de diferente tipo para el desarrollo de destrezas de visualización tridimensional y que permitan modelizar conceptos matemáticos tridimensionales. De esta forma, se pretende generar diferentes representaciones de una misma figura tridimensional a partir de herramientas como los programas de modelado tridimensional, la Realidad Aumentada o la Realidad Virtual, en línea con el Diseño Universal de Aprendizaje (DUA). La propuesta que se presenta se ha llevado a cabo en un contexto de resolución de problemas de matemáticas con alumnado de último curso de Educación Secundaria. Los resultados muestran la preferencia de herramientas diferentes dependiendo de los diferentes contextos de los problemas propuestos.
Palabras clave
Diseño Universal de Aprendizaje (DUA), Geometría Tridimensional, Realidad Aumentada, Realidad Virtual, Modelización Geométrica, Visualización.
Abstract
The use of technological tools in teaching geometry concepts can be a strategy that promotes the design of inclusive proposals aimed at preventing potential difficulties. Therefore, the objective of this communication is to present various types of technological resources for the development of three-dimensional visualization skills and to enable the modeling of three-dimensional mathematical concepts. In this way, the intention is to generate diverse representations of the same three-dimensional figure using tools such as three-dimensional modeling programs, Augmented Reality, or Virtual Reality, in line with Universal Design for Learning (UDL) principles. The proposed approach has been implemented in the context of mathematics problem-solving activities with high school students. The results reveal a preference for different tools depending on the various contexts of the problems presented.
Keywords
Universal Design for Learning (UDL), Three-Dimensional Geometry, Augmented Reality, Virtual Reality, Geometric Modelling, Visualization.
Introducción
En la actualidad, el estudiantado de niveles universitarios y preuniversitarios utiliza diferentes tipos de dispositivos para el afianzamiento de los conceptos vistos en el aula. El tradicional uso de libros, apuntes y calculadoras ha evolucionado a la consulta de referentes de diferente índole a través de Internet, así como de otras herramientas que favorecen la comprensión de los conceptos. De hecho, el Real Decreto 217/2022 [1] por el que se establecen las enseñanzas mínimas de la Educación Secundaria Obligatoria indica, en la materia de matemáticas, que está diseñado con el objetivo de “facilitar el desarrollo de unas matemáticas inclusivas que permitan el planteamiento de tareas individuales o colectivas, en diferentes contextos, que sean significativas para los aspectos fundamentales de las matemáticas”. Como se indica posteriormente, “se ha de potenciar el uso de herramientas tecnológicas en todos los aspectos de la enseñanza-aprendizaje ya que estas facilitan el desarrollo de los procesos del quehacer matemático”. Es por esto que, siguiendo las directrices del Diseño Universal de Aprendizaje (DUA) [2], una de las estrategias que favorece el diseño de actividades inclusivas es la búsqueda de diferentes formas de representar los contenidos de aprendizaje; más concretamente, en la búsqueda de diferentes opciones que favorezcan la percepción, la notación y la comprensión.
Estas directrices que se presentan tanto en el currículo como en el DUA tienen una aplicación directa en las matemáticas y, en concreto, en el desarrollo de habilidades de visualización entre el alumnado. Proporcionar a los estudiantes formas alternativas de visualizar los objetos tridimensionales a partir del uso de herramientas tecnológicas de diferente tipo puede, por tanto, prevenir la aparición de problemas en el aprendizaje de los conceptos geométricos y favorecer la comprensión de los conceptos geométricos asociados [3].
Por todo esto, el objetivo de esta propuesta es el de presentar diferentes alternativas para la generación de propuestas educativas dirigidas al proceso de enseñanza-aprendizaje de los conceptos matemáticos que se pueden modelizar mediante objetos tridimensionales a través de la utilización de aplicaciones móviles. Para ello se pretende presentar las características de la elaboración de estos recursos educativos junto al estudio comparativo realizado con alumnado del último curso de Educación Secundaria.
Metodología
Herramientas tecnológicas para la visualización 3D
Los avances de los últimos años en el diseño de programas de modelización, que anteriormente se usaban en la arquitectura o la ingeniería, han permitido simplificar las interfaces de usuario y las ha convertido en más accesibles e inclusivas para su posible aplicación en entornos educativos. Actualmente, se pueden encontrar tecnologías de diferente tipo:
Herramientas para el modelado tridimensional (PM3D). Los programas de Diseño Asistido por Computadora (CAD) han generado versiones alternativas y que presentan finalidades educativas, como TinkerCAD o BlocksCAD. Estos programas utilizan diferentes estrategias para generar, a partir de unas formas primitivas, formas geométricas tridimensionales más complejas.
Herramientas para la Realidad Aumentada (RA). Los programas de RA utilizan marcas de diferente tipo para incluir información adicional (en formato audio, imagen y/o vídeo) a la información captada por una cámara. Los objetos tridimensionales quedan, por tanto, integrados en la visualización del entorno. Existen diferentes alternativas como la RA con marcas planas (como los códigos QR) y la RA con objetos (como los cubos holográficos).
Herramientas para la Realidad Virtual (RV). A diferencia de la RA, en los programas de RV el usuario se integra en un mundo virtual donde se encuentran los objetos tridimensionales y donde se puede interactuar con ellos o visualizar desde diferentes ubicaciones. Los programas, como CoSpaces, permiten su utilización mediante dispositivos sencillos, como dispositivos móviles, o en dispositivos más elaborados como las gafas de RV.
Para la propuesta realizada, se han diseñado cuatro alternativas tecnológicas en línea con las tecnologías presentadas: Programa de Modelado Tridimensional (PM3D), Realidad Aumentada con marcas planas (RA), Realidad Aumentada a través de un cubo holográfico (HOLO) y Realidad Virtual a través del programa CoSpaces (RV). Como ejemplo, se va a mostrar las diferentes alternativas para la visualización de la triple forma o tritapón que se presentó con detalle en [4]. Para ello, se presentan los enlaces que permiten acceder a los elementos creados, así como las capturas de pantalla que muestran un fotograma dentro de las posibilidades que estas herramientas ofrecen:
- PM3D: A través del programa de modelado tridimensional se puede generar paso a paso, desarrollando habilidades de pensamiento computacional generalmente, figuras geométricas tridimensionales. En la página https://www.tinkercad.com/things/a6IYnMujUjA se puede encontrar tanto la Triple Forma como el proceso de construcción de esta que se puede encontrar detallado en [4].
- RA: A través del programa de RA denominado Assemblr (https://www.assemblrworld.com/) y de su aplicación móvil con finalidad educativa, Assemblr EDU, el alumnado puede visualizar los objetos tridimensionales en RA mediante el uso de marcadores.

- HOLO: Mediante el marcador tridimensional en forma Cubo Holográfico Merge, el programa Merge EDU (http://www.mergeedu.com/) permite una experiencia de RA manipulativa. La posibilidad de mover con la mano el cubo permite seleccionar manualmente la orientación del objeto tridimensional que se visualiza a través del dispositivo móvil.

- RV: Sobre el programa CoSpacesEDU (https://cospaces.io/edu/) el alumnado puede introducirse en un mundo donde se pueden encontrar los objetos tridimensionales. Para ello, se puede utilizar un dispositivo móvil complementado con unas gafas de RV o algo más elaborado como las Cardboard de Google. La plataforma también permite introducirse en el mundo sin necesidad de usar gafas especiales; de esta forma, se puede pasear por los mundos generados con un estilo similar al de los videojuegos (se puede consultar en https://edu.cospaces.io/QUW-FEJ).

Estudio comparativo de las herramientas tecnológicas
La propuesta del uso de herramientas alternativas para favorecer la visualización de objetos matemáticos tridimensionales se ha llevado a cabo en un taller extraescolar de resolución de problemas de geometría con 4 estudiantes de 4o de E.S.O. de un centro educativo privado de la Comunidad Valenciana en el mes de junio de 2021. Para poder llevarlo a cabo el alumnado participante disponía de las herramientas de visualización presentadas en el punto anterior como recurso tecnológico de apoyo para la resolución de una secuencia de problemas de geometría en los que la visualización era una destreza clave. Con anterioridad a la resolución de los problemas y durante una sesión de 50 minutos, se instruyó al alumnado en el uso de cada una de las cuatro herramientas con el objetivo de facilitar su uso en la tarea posterior. Algunos de los problemas propuestos para el estudio de la esponja de Menger eran los siguientes:
- Explica cómo construirías la Esponja con 3 iteraciones ¿por composición o por eliminación?
- Observa una representación 3D de la esponja de Menger después de la tercera iteración. ¿Cuántos “túneles” atraviesan completamente la figura en cada dirección (x, y, z)?
- Al mirar la esponja de Menger desde arriba después de varias iteraciones, identifica la simetría presente en la figura. ¿Cuántos ejes de simetría puedes encontrar?
- Al rotar la esponja de Menger en diferentes ejes, ¿cómo varía su apariencia? ¿Hay algún eje en el que la rotación parezca no tener agujeros al otro lado?
- Piensa en la esponja de Menger como un laberinto tridimensional. Si entras desde un agujero en una esquina, ¿podrías encontrar un camino que te lleve al centro? Explica y justifica tu respuesta basándote en tus observaciones.
- Si la segunda iteración del cubo de Menger estuviera construida por cubitos pequeños pegados y le pintamos las caras exteriores del cubo original, ¿cuántos “cubitos” quedarían sin pintar? ¿Y después de la tercera iteración?
Una vez realizada la secuencia de problemas en los que se analizaban detalladamente las figuras geométricas de la triple forma y la esponja de Menger, el alumnado disponía de un cuestionario de preferencias de las herramientas usadas en la resolución de los problemas. El instrumento de análisis usado ha sido dicho cuestionario formado por dos preguntas: una pregunta de ordenación de la preferencia de las herramientas usadas y otra de respuesta abierta en la que el alumnado puede desarrollar su percepción de la usabilidad de las herramientas usadas y argumentar las decisiones tomadas en la pregunta anterior.
Resultados y discusión
Los datos que se presentan corresponden a las respuestas de todos los participantes en el taller extraescolar a la pregunta de ordenación y a una selección de las respuestas a la pregunta abierta realizada por los firmantes de la comunicación. En relación a la ordenación de las preferencias de las diferentes herramientas utilizadas en el taller de resolución de problemas se obtienen los siguientes resultados para la visualización de la triple forma y del Cubo de Menger:
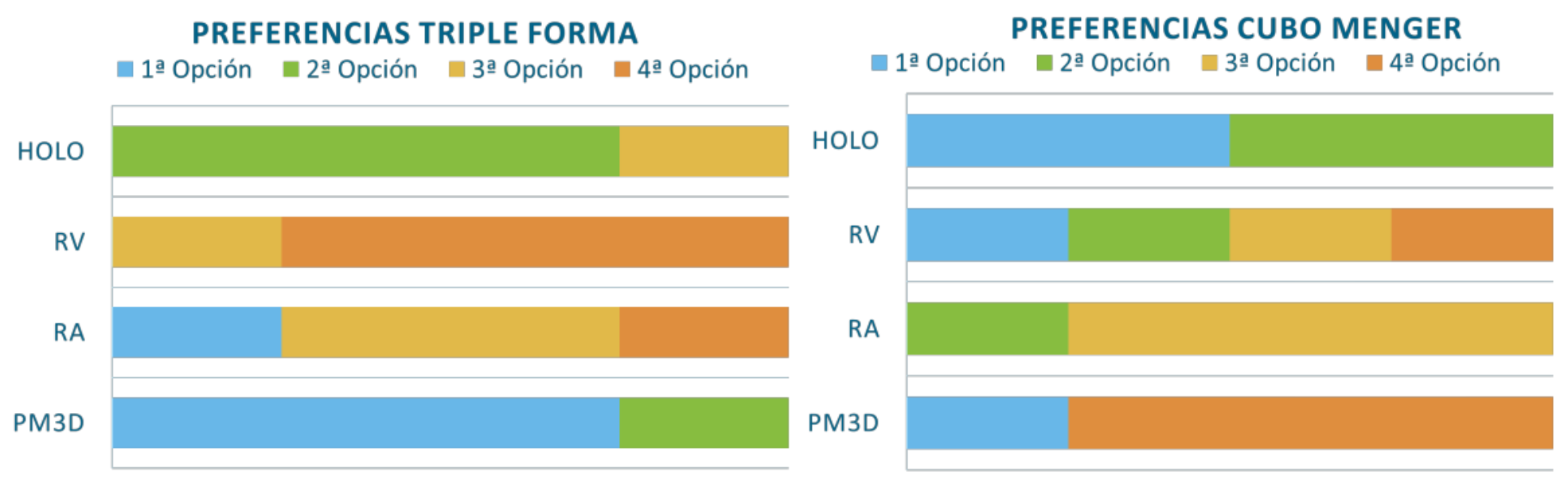
Entre las herramientas disponibles, destaca la preferencia del programa de modelado tridimensional (Tinkercard) para el análisis de la triple forma, ya que “permite analizar completamente la figura en todas sus perspectivas” (Alumno 2) y “ver cómodamente la figura desde distintos ángulos” (Alumno 3). En segundo lugar, dentro de las preferencias de casi todos los alumnos, se encuentra el cubo holográfico dado que, como también menciona el Alumno 3, “también permite visualizar la forma desde los distintos ángulos”.
Sin embargo, para el estudio de la esponja de Menger, “la forma cúbica del cubo [holográfico] mejora su observación” (Alumno 1). Destaca, además, la baja preferencia otorgada al programa de modelado tridimensional debido, principalmente, a la forma análoga de todas las caras de la esponja de Menger.
En general, el alumnado prefiere la utilización de la realidad aumentada a través del cubo holográfico frente al uso de la aplicación Assemblr por la manipulación directa del objeto. Entre las principales limitaciones de la realidad virtual para la visualización se encuentra la imposibilidad de modificar el ángulo de visionado, en concreto, para poder visualizar los objetos desde la parte superior o inferior.
Conclusiones
Las diferentes representaciones generadas de las figuras geométricas han permitido a los estudiantes seleccionar sus herramientas preferidas para dar respuesta a los retos planteados. Los resultados y el uso de las herramientas realizado por parte del alumnado sugiere la necesidad de usar diferentes herramientas dependiendo de las características de las formas geométricas y de los problemas asociados. A su vez, las herramientas alternativas presentadas favorece el diseño de actividades siguiendo el Diseño Universal de Aprendizaje propiciando el uso de múltiples formas para la representación, así como para la acción y la participación del alumnado.
Entre las limitaciones del estudio que se presenta se encuentra el reducido número de participantes en la experimentación. Además, podría ser de interés realizar este mismo estudio en un aula de docencia curricular de cuarto curso de Educación Secundaria. Otra limitación que se ha encontrado para un estudio más numeroso es la necesidad de disponer de herramientas tecnológicas para todo el alumnado.
Como trabajo futuro, se puede realizar un estudio comparativo entre el uso de herramientas tecnológicas que favorezcan la visualización y los materiales manipulativos, como puede ser la impresión 3D. En concreto, las figuras diseñadas a través de los programas de modelado tridimensional se pueden construir mediante la impresión 3D. Por ello, puede ser de interés analizar la preferencia entre los diferentes recursos educativos para la ayuda en la resolución de problemas de geometría tridimensional.
Referencias
[1] Real Decreto 217/2022, de 29 de marzo, por el que se establece la ordenación y las enseñanzas mínimas de la Educación Secundaria Obligatoria. Boletín Oficial del Estado, 76, de 30 de marzo de 2022, 1–198. Página web.
[2] CAST. Universal Design for Learning Guidelines, version 2.0. Wakefield, MA: Center for Applied Special Technology. 2011.
[3] Kondo, Y., Fujita, T., Kunimune, S., Jones, K., Kumakura, H. The influence of 3D representations on students ́ level of 3D geometrical thinking. En* Proceedings of the Joint Meeting PME 38 and PME-NA 3*6; Liljedahl, P., Oesterle, S., Nicol, C., Allan, D., Eds.; Vol. 4; Vancouver: PME, 2014, pp. 25–33.
[4] Rotger, L., Ribera, J. M. Visualizando las matemáticas en la tercera dimensión a través de Tinkercad. En Actas de las I JID+, Jornades d’Innovació Docent en Matemàtiques en Educació Superior; Valencia, 2021; pp. 63–69. ISBN: 978-84-09- 32639-6.