Matemáticas… ¡Me aburro!
Resumen
Trabajar la predisposición de la sociedad en general y de los estudiantes en particular hacia las matemáticas es una tarea clave para todo docente. Fomentar el pensamiento lógico matemático y el acercamiento a las matemáticas es necesario en un mundo donde el conocimiento de esta ciencia es simplemente necesario para cualquier ciudadano y, especialmente, para los universitarios. Esta ponencia plantea un acercamiento al razonamiento lógico y a la utilidad de las matemáticas a través de la diversión y la competición de la mano del desarrollo de estrategias para asegurarse la victoria en diversos juegos.
Palabras clave
Desarrollo del pensamiento lógico matemático, Divulgación matemática, Matemáticas y juegos, Estrategia ganadora.
Abstract
Working on the predisposition of society in general as well as students, particularly, towards mathematics is a key task for every teacher. Developing logical mathematical thinking and forming an approach to mathematics is required for a better understanding of our world, especially for university students. This paper presents an approach to logical reasoning, but also shows the usefulness of mathematics with various strategies to insure victory in all kinds of different games.
Keywords
Development of logical mathematical thinking, Usefulness of mathematics, Mathematics in games, Winning strategy.
Introducción
Quizás estamos abusando demasiado de ciertos comentarios relativos a las Matemáticas que pueden desembocar en que nuestros estudiantes, al igual que parte de la ciudadanía en general, estén en cierto modo hartos de escuchar que:
- Las Matemáticas son muy importantes.
- Son necesarias para todo.
- Hay Matemáticas por todos lados.
- Las Matemáticas son DIVERTIDAS.
Pero la verdad es que lo que sí puede gustar, lo que sí es divertido es JUGAR, y más allá de jugar… GANAR.

De esta forma, si enseñamos que las Matemáticas pueden dar la oportunidad de disfrutar, de sacar partido a los juegos y más allá, de asegurarte la victoria, estaremos fomentando el interés por esta ciencia y las ganas de explorar, aprender y entender sus estrategias. Se mostraría entonces que, así como el razonamiento matemático puede resultar muy útil en la vida académica, también puede ayudarte a disfrutar en tu vida cotidiana y en la relación con tu entorno, por ejemplo, jugando y ganando. Quedaría latente que las Matemáticas pueden abrir una puerta para disfrutar más.
La RAE (Real Academia Española) define el juego como un “Ejercicio recreativo o de competición sometido a reglas, y en el cual se gana o se pierde”. Con esta idea, en este artículo se presentarán diversos juegos en los que, a través de la estrategia lógico matemática se analiza si es posible asegurarse la victoria y en su caso, cómo hacerlo [4].
La finalidad entonces es presentar un planteamiento lúdico de esta ciencia que pueda ser usado para el acercamiento y el fomento del gusto y el interés por ella [1], [2]. Demostrar que conviene tener algo de “matemático” incluso para jugar y salir victorioso en una tarde de juegos con los amigos.
“El juego y la belleza están en el origen de una gran parte de las matemáticas. Si los matemáticos de todos los tiempos se lo han pasado tan bien jugando y contemplando su juego y su ciencia, ¿por qué no tratar de aprenderla y comunicarla a través del juego y de la belleza?”Miguel de Guzmán
Juegos
Con la finalidad de dejar constancia de la importancia de las Matemáticas para ganar en ciertos juegos y con ello asegurar un estado de satisfacción y disfrute, se plantean algunos retos en los que el conocimiento y razonamiento matemático ayuda a buscar y/o encontrar una estrategia ganadora. Con estrategia ganadora se quiere decir “estrategia mediante la cual uno de los jugadores, el primero o el segundo, se asegura ganar la partida”. Esto siempre que los dos jugadores jueguen de forma ideal, es decir, en todo momento realicen movimientos lógicos encaminados a ganar la partida.
Juegos clásicos
a) Las tres en raya:
Este juego no tiene gracia. Perder es prácticamente imposible: empieza el 1o poniendo, normalmente, en el centro, el otro contesta y, a partir de allí, todo es fastidiar al contrario. No puedes perder, termina siempre en empate. Es un juego en el que se puede jugar perfecto, hay una estrategia para jugar perfecto. En estos casos los jugadores empatan, no hay estrategia ganadora para ninguno de los jugadores. La mejor estrategia es un empate.
De esta forma, el razonamiento lógico, las Matemáticas, demuestran que este juego no tiene estrategia ganadora.
b) Las damas
Para este juego, también se demostró (2007) que se puede jugar perfecto. Si así lo hacen los 2 jugadores, se termina en tablas.
Lo que pasa es que, para las damas, esta estrategia es más compleja, no es tan fácil jugar perfecto y por ello puede tener interés jugar una partida de damas con alguien. Desde luego, estos juegos en los que se puede jugar perfecto, son muy malos para jugar con el ordenador ya que es posible programarlos para jugar perfecto.

c) El ajedrez
En este juego, la cosa se complica. No se sabe si se puede jugar perfecto, si existe una estrategia ganadora. Los matemáticos están en ello, pero existen tantas posibilidades de jugadas que no es posible hasta ahora diseñar la estrategia perfecta. Pero sí se programa a los ordenadores para que lo hagan muy bien. De hecho, ya un ordenador ha ganado al maestro del ajedrez Kaspárov.

Propuestas sencillas para hacer pensar
Si como parece ser evidente, lo importante y motivante es ganar, las Matemáticas pueden ayudar en el juego y, de esta forma, transmitir que desarrollar el pensamiento lógico matemático se vea como una herramienta vital. A continuación, se presentan algunos sencillos retos que pueden plantearse fácilmente para captar la atención y fomentar el interés por “saber” Matemáticas y que hacen pensar. Pueden entonces utilizarse como herramientas de estímulo y de acercamiento a esta ciencia [4], [5].
Uno posible propuesta es realizarlos con los estudiantes. Primero ganar a algún voluntario que se atreva con el desafío, luego dejar que todos jueguen por parejas para que descubran cuál es la estrategia a seguir para asegurarse la victoria. Después explicar la metodología para todos.
a) Juego de retirar monedas
Este juego para dos jugadores consiste en situar, en este caso 12 monedas en la mesa y en que cada jugador elimina por turnos monedas: una o dos (si se eliminan 2 deben estar contiguas, juntas, no puede haber huecos entre ellas). Gana el que elimina la última moneda.

Experimentando un poco, el razonamiento permite deducir que, para este juego, existe estrategia ganadora para el segundo jugador. Esta es:
- Siempre quitar el mismo número de monedas que tu adversario.
- En la primera respuesta dejar divididas las monedas en dos partes iguales desconectadas.
- Luego hacer lo que hace el adversario en el bloque opuesto. Hacerlo de forma simétrica.
b) Fila de monedas
En este reto se tienen 6 monedas de diferentes valores, los que se quieran seleccionar y se colocan como quiera la victima del juego.
La idea es ir quitando por turnos una moneda siempre de los extremos. El jugador que al final se queda con mayor valor gana, si hay empate gana el que ha propuesto el juego.

Para este reto, pensando y experimentando un poco, puede descubrirse que existe estrategia ganadora para el primer jugador, válido para cualquier número de monedas par.
La idea consiste en dividir mentalmente las monedas en dos bloques: \[ \mathrm{XYXYXY} \] Sumando cada uno de los valores de esos dos bloques, uno u otro vale más o suman lo mismo.
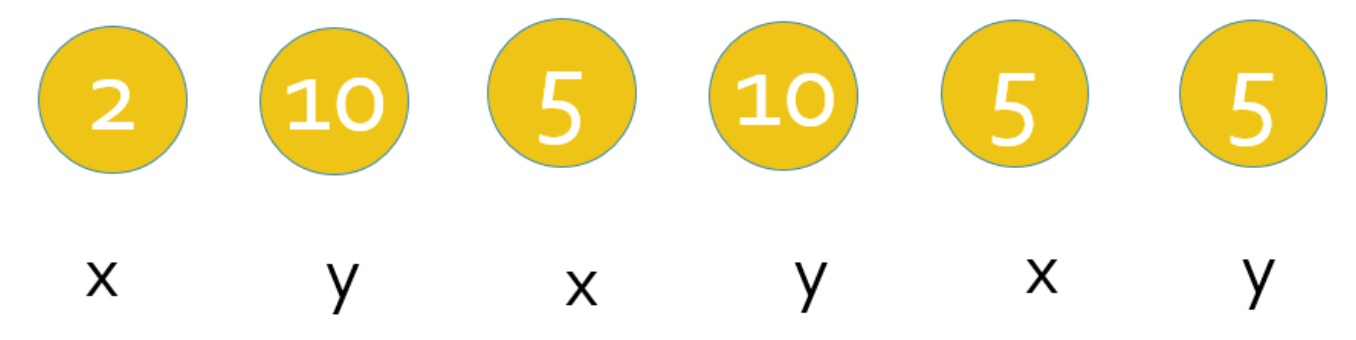
La estrategia del primer jugador consiste es escoger el bloque que suma más. Como comienza él, elije una moneda del conjunto que vale más, su contrario va forzado a coger del otro conjunto, el que vale menos, y así sucesivamente. Pese a que a simple vista parece una estrategia sencilla, no suele captarse rápidamente y es conveniente jugar con diversas disposiciones de las monedad. Una vez presentado y trabajado este reto, puede ser buen momento para ampliar el estudio introduciendo el Teorema de la Pizza [6]:
Decides cenar con tu amigo y pedís una pizza. Cuando llega la comida, la pizza está cortada en ocho trozos y en condiciones ideales, es decir, que los cuatro cortes pasen por el centro y estén igualmente espaciados, lo que significa que están formando un ángulo de 45o entre cada dos de ellos, estos serán completamente iguales. En ese caso, repartir la pizza, es fácil, si cada uno de vosotros va cogiendo un trozo de los extremos, cada comensal comerá exactamente lo mismo.
Pero lo normal es que esos cortes realizados en la pizzería no sean tan perfectos y los cortes no coincidan en el centro de la pizza ¿Se podrá repartir de todas formas la comida a partes iguales? Pues las Matemáticas ayudan.
Teorema de la pizza: Si una pizza es dividida en ocho trozos, obtenidos mediante cuatro cortes que pasan por un punto común y forman un ángulo de 45º entre ellos, entonces la suma de las áreas de los trozos alternos son iguales.
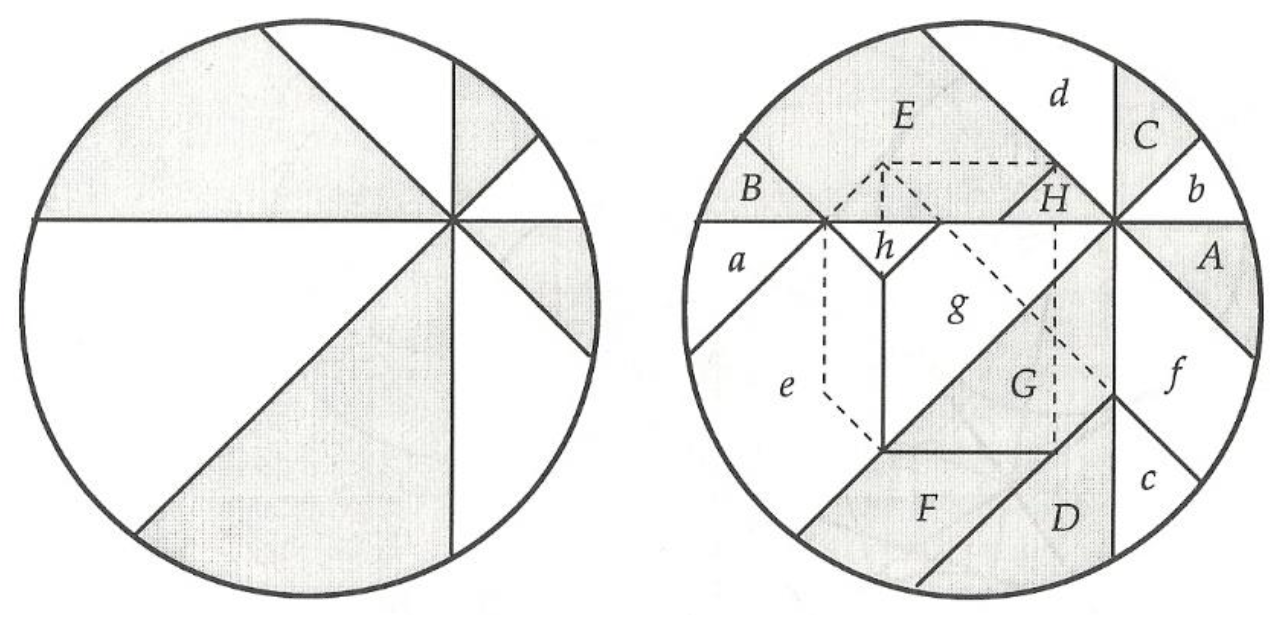
Nota: el teorema sigue siendo cierto para un número de cortes par mayor que 2, es decir, 4, 6, 8, etc. Una demostración ha sido dada por Greg Frederickson [3]. No es cierto para 2 cortes ni para un número impar de cortes.
c) El problema de Josefo
Este problema se le atribuye a Flavio Josefo quién vivió en la región de Alejandría en el primer siglo. Se cuenta que asediado por los romanos en una cueva con sus tropas propuso que, para evitar ser capturados y vendidos como esclavos, muriesen y, para cumplir esta macabra decisión, decidieron que se colocarían en círculo con los lugares numerados y se matarían entre ellos con una espada siguiendo el siguiente procedimiento: El primero mataría al segundo y pasaría la espada al tercero, el cual acabaría con al cuarto, pasaría la espada al quinto y así se seguía el ciclo sucesivamente, hasta que quedara uno solo, el cual se quitaría la vida él mismo. Milagrosamente él se salvó ¿sabía Matemáticas?
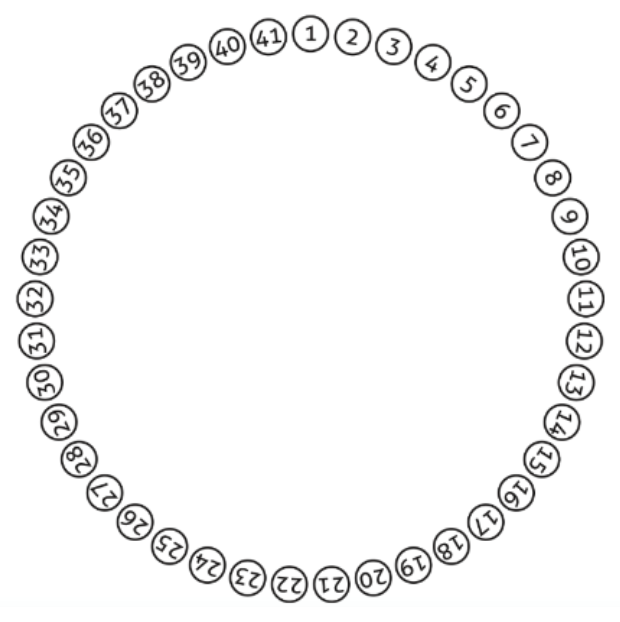
Analicemos de forma “matemática” el problema. Un primer paso realizar un tanteo para algunos casos según el número de participantes:
Resultados según el número de jugadores:
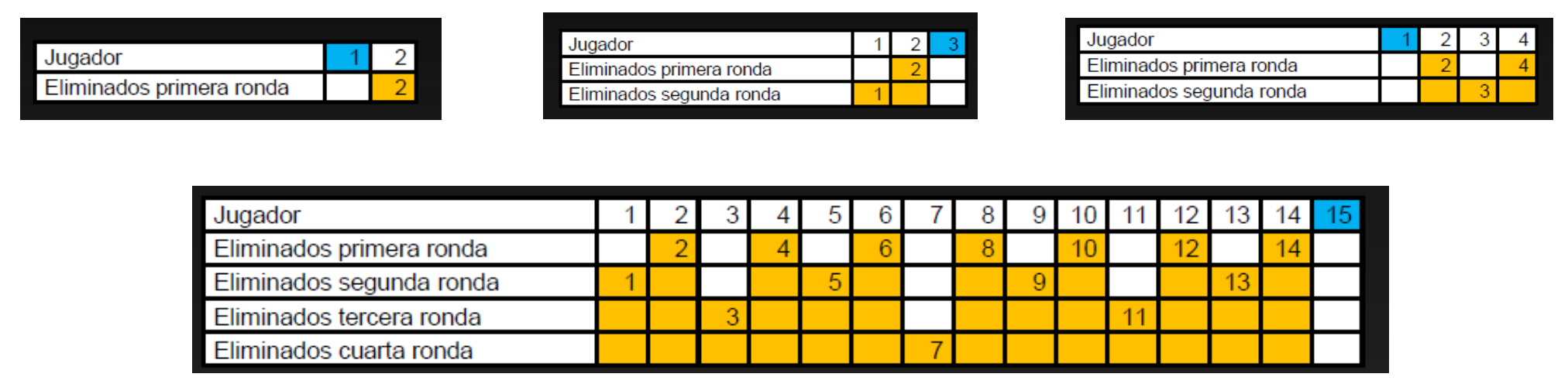
De esta forma es posible generar esta tabla con posiciones “ganadoras” según el número de implicados:

¿Qué se puede deducir?:
- Las posiciones ganadoras son siempre números impares. Si te colocas en una posición par, sea cual sea el número de implicados, estas muerto: pierdes.
- Cuando el número de jugadores es una potencia de 2 (2, 4, 8, 16,…) la posición ganadora es la número 1.
- Cuando el número de implicados no es potencia de 2, el ganador ocupa siempre una posición impar desde 3 en adelante. El número estará comprendido entre dos potencias de 2 y la posición ganadora serán sucesiones de números impares que comienzan desde 3 y están formadas por tantos términos como lugares haya entre las potencias de 2.
Veamos un ejemplo de cómo calcular la posición ganadora, por ejemplo para 23 jugadores:

23 está comprendido entre las potencias de 2, 24=16 y 25=32. Asignamos entonces posiciones ganadoras desde 16 a 23 jugadores sabiendo que en 16 está el 1 y luego vamos con sucesión de impares. A 23 le toca el 15, 15 será entonces el sitio que debes elegir para ganar.
Estos han sido solo tres ejemplos de los muchos retos que pueden proponerse y en los que una estrategia razonada puede asegurarte la victoria. Conocerlos y utilizarlos pueden ser una fuente motivadora para el fomento y el gusto por las Matemáticas.
Conclusiones
Jugar es motivante y sobre todo es divertido. De esta forma, jugar y ganar usando las Matemáticas, la lógica y el razonamiento debería ser mucho más entretenido.
En este trabajo se ha propuesto una pequeña muestra de retos donde la capacidad de razonar, la abstracción y la utilización de ciertos conceptos matemáticos permiten deducir si existe una estrategia ganadora y, en su caso, diseñarla. Usar este tipo de acciones puede ser una herramienta muy útil para atraer a los estudiantes en particular y la sociedad en general a las Matemáticas y hacerla más atractiva.
Referencias
[1] Deulofeu, J. Prisioneros con dilemas y estrategias dominantes. Teoría de juegos. Colección “El mundo es matemático”. RBA (2011).
[2] Deulofeu, J, M.EDO. Investigación sobre juegos, interacción y construcción de conocimientos matemáticos. Enseñanza de las Ciencias, 24 (2), 257-268 (2006).
[3] Frederickson, G. The Proof Is in the Pizza, Mathematics Magazine 85, 26–33 (2012).
[4] Sáenz, E. Inteligencia Matemática. Plataforma (2016).
[5] Sotornil, D. ¿A qué quieres que te gane? SUMA, 98, 59-67 (2021).
[6] Upton, L. J. Problem 660, Mathematics, 41 (1): 46 (1968).