Planteamiento de Problemas Matemáticos como parte de la formación matemática de los futuros docentes
Resumen
El planteamiento eficaz de problemas matemáticos es fundamental para una enseñanza de las matemáticas de alta calidad y por lo tanto los docentes deben ser capaces de formular y plantear problemas que supongan un reto para su alumnado. En este trabajo se presenta una intervención diseñada para mejorar la competencia en planteamiento de problemas de los futuros docentes. Esta intervención se ha aplicado en varios grupos de una de las asignaturas del Grado en Maestro/a en Educación Primaria de la Universitat de València. Como consecuencia, el alumnado ha podido profundizar en algunas de las definiciones actuales de problema de alta demanda cognitiva y desarrollar competencias que le permitirán plantear problemas de calidad que promuevan el desarrollo cognitivo matemático de sus alumnos.
Palabras clave
Planteamiento de problemas, niveles de demanda cognitiva, formación futuros maestros.
Abstract
Effective mathematical problem posing is fundamental to high quality mathematics teaching and therefore teachers must be able to formulate and pose challenging problems for their students. This paper presents an intervention designed to improve the problem-posing competence of future teachers. This intervention has been applied in several groups of one subject of the Degree in Teacher in Primary Education. As a result, students have been able to deepen their understanding of some of the current definitions of problems with high cognitive demand and develop competences that will allow them to pose quality problems that promote the mathematical cognitive development of their students.
Keywords
Problem posing, levels of cognitive demand, teaching future teachers.
Introducción
Por Planteamiento de Problemas Matemáticos (PPM) nos referimos a varios tipos de actividades relacionadas que implican que el profesorado o su estudiantado formule (o reformule) y exprese un problema o tarea en función de un contexto particular [3]. Brown y Walter [2] defendieron la importancia del planteamiento de problemas en el aprendizaje de las matemáticas.
Argumentaron que llegar a comprender las matemáticas está intrínsecamente relacionado con la generación y exploración de preguntas. El planteamiento de problemas aparece junto a la resolución de problemas en los documentos curriculares que recomiendan al profesorado que introduzca actividades de planteamiento de problemas para su alumnado [8]. Sin embargo, el estudiantado de matemáticas a todos los niveles tiene generalmente pocas oportunidades de construir y plantear sus propios problemas [5].
El planteamiento eficaz de problemas es una de las competencias que el alumnado de magisterio debe desarrollar [7]. Sin embargo, la realidad de la mayoría de las aulas escolares es que los problemas de matemáticas provienen de los libros de texto [5]. Aprender a evaluar la calidad de las tareas matemáticas antes de plantearlas al alumnado forma parte de lo que se debe aprender en los cursos de preparación docente [4]. El trabajo en el planteamiento de problemas matemáticos de calidad es útil en el desarrollo profesional del profesorado para (a) comprender el pensamiento del alumnado, (b) desarrollar la competencia matemática del profesorado y (c) ayudar al profesorado a plantear problemas de calidad [3]. Por su parte, Crespo [4] afirma que, aunque el profesorado en activo o en formación, defiende creencias y visiones de la enseñanza de las matemáticas en las que se ven a sí mismos como docentes que plantean problemas matemáticos interesantes y valiosos, no están bien preparados para traducir su visión a la realidad del aula. Por tanto, aunque la definición precisa de un problema matemático matemáticamente interesante o de calidad varía según el contexto y el propósito del estudio, es una cuestión importante cómo se puede apoyar a profesorado en formación o en activo para que planteen este tipo de problemas [3].
En esta propuesta se aborda el trabajo de PPM con futuros maestros y futuras maestras de la Facultat de Magisteri de la Universitat de València. Desde el enfoque profesional, recibirán una formación que consistirá en el desarrollo de criterios y estrategias para identificar y juzgar la calidad de los problemas matemáticos. Además, el propio estudiantado planteará problemas cuyos enunciados serán analizados y evaluados dentro del aula tras su resolución. Se incluirán marcos explícitos y esquemas de clasificación como el marco de “demanda cognitiva de las tareas” de Smith y Stein [13], para formar al profesorado en formación, no solamente en analizar, seleccionar y crear las tareas que podrían utilizar con su alumnado, sino también en desarrollar estrategias para realizar adaptaciones que mantengan o aumenten la demanda cognitiva de las tareas elegidas. Además, se abordará una formación en los diferentes tipos de problemas matemáticos que se pueden plantear y se analizará si el alumnado es capaz de distinguir y transferir las características de cada tipo de problema.
En este proyecto se pretende, fundamentalmente, dar respuesta a la pregunta ¿qué nivel de calidad tienen los problemas planteados por futuros docentes antes y después de una formación en PPM?
Metodología
La muestra sobre la que se ha realizado la investigación está formada por cinco grupos matriculados en la asignatura de Didáctica de la Geometría, Medida, Estadística y Probabilidad de 4o curso del Grado de Maestro/a en Educación Primaria de la Universitat de València en el curso académico 2022-23.
El proyecto se ha estructurado en tres fases. En la primera fase, se propuso al alumnado participante, a modo de pretest, una tarea con una duración de 30 minutos. Esta tarea estaba formada por dos partes y para su realización no se había recibido ninguna formación previa. La primera parte consistía en plantear individualmente un problema matemático para estudiantes de 6o de Educación Primaria dado un contexto concreto. A cada estudiante se le asignó uno de los siguientes contextos: Valla publicitaria; Gallinero y gallinas; Jardinero municipal; Pastor de ovejas; Frutero en puesto del mercado; Taxista; Ascensor edificio +10 pisos; Maternidad de un hospital; Entrenador de un equipo deportivo; Valla publicitaria. En la segunda parte debían predecir la respuesta del alumnado de 6o de EP al problema planteado proponiendo una posible solución.
En la segunda fase, se implementó una formación en PPM con una duración de 2 sesiones de 2 horas. En cuanto a los contenidos, se abordaron conceptos y procedimientos relacionados con los tipos de tareas matemáticas [1,10], los niveles de demanda cognitiva [13], los criterios de clasificación de los problemas matemáticos [1], la definición de problema matemático [9,11,12], los modelos y heurísticos de resolución de problemas [10] y el PPM [3]. Además, el desarrollo de las sesiones incluía oportunidades para debatir en grupo, resolver, analizar y plantear problemas matemáticos.
En la tercera fase, se realizó un postest que consistía en una tarea similar a la del pretest. Los participantes disponían de 30 minutos para plantear de manera individual dos problemas matemáticos a partir de una situación dada para alumnado de 6o de Educación Primaria. Pero, en este caso, debían ajustarse a dos condiciones: un nivel elevado de demanda cognitiva en ambos problemas, y diferentes en cuanto al tipo de final (abierto y cerrado). Al igual que en el pretest, tenían que predecir las respuestas de los estudiantes de 6o de Educación Primaria y resolver los problemas. Asimismo, en esta ocasión se incorporó una tarea adicional en la que el alumnado se organizaba en pequeños grupos para reflexionar, analizar y debatir sobre las características de los problemas planteados por cada integrante, según lo estudiado previamente en las sesiones de la intervención, la idoneidad del enunciado, cómo mejorarlo o incluir nuevos elementos, y buscar soluciones alternativas al problema. Esta tarea se llevó a cabo de forma oral y no fue objeto de análisis explícito de este estudio, sino que formó parte de la formación que recibió el alumnado.
A partir de la muestra total de los cinco grupos, con más de 200 estudiantes, se ha seleccionado de forma aleatoria una submuestra más reducida y manejable con un tamaño de 40 sujetos, con lo que se han obtenido 40 problemas pretest y 80 problemas postest. Los problemas planteados se analizaron aplicando el instrumento de evaluación de la calidad de problemas matemáticos para Educación Primaria, F-PosE, diseñado por Leavy y Hourigan [6] (Tabla 1).
| Ítems de evaluación | Niveles de evaluación |
|---|---|
| Contexto interesante y motivador | 5 niveles: ausente, débil, adecuado, bien y excelente |
| Claridad en el lenguaje y en el contexto cultural | 5 niveles: ausente, débil, adecuado, bien y excelente |
| Coherencia con el currículum | 5 niveles: ausente, débil, adecuado, bien y excelente |
| Atención a la demanda cognitiva | 3 niveles: bajo, medio y alto |
| Número apropiado de pasos en la resolución para promover el razonamiento | 2 niveles: un paso y múltiples pasos |
| Variedad de estrategias de resolución | 2 niveles: sí y no |
| Facilitar múltiples soluciones | 2 niveles: sí y no |
| Oportunidad de éxito | 5 niveles: ausente, débil, adecuado, bien y excelente |
Resultados
A cada uno de los problemas analizados mediante un análisis de triangulación de expertos, se le ha asignado una calificación de entre 0 y 8 puntos. Estas puntuaciones se han agrupado en intervalos de manera que, los problemas con una puntuación superior a 0 e inferior o igual a 4 se han considerado de calidad insuficiente, los problemas con puntuaciones entre 4 y 7 se les ha atribuido una calidad moderada y los problemas con una calificación igual o superior a 7 se les ha asignado una calidad sobresaliente.

En el problema de la Figura 1, los estudiantes sólo tienen que localizar los triángulos presentes en la imagen y recordar la clasificación de los triángulos según sus ángulos y sus lados. Tal y como se ha puntuado en la Tabla 2, no promueve el razonamiento de los estudiantes, no se puede resolver con diversas estrategias de resolución ni facilita múltiples soluciones.


En los problemas mostrados en la Figura 2 y la Figura 3 encontramos ejemplos de problemas que promueven el razonamiento de los estudiantes y en los que se pueden utilizar una variedad de estrategias de resolución que faciliten múltiples soluciones. Las puntuaciones de estos problemas se encuentran, también, en la Tabla 2.
| Indicador | Puntuación Problema 1 | Puntuación Problema 2 | Puntuación Problema 3 |
|---|---|---|---|
| Contexto interesante y motivador | Adecuado – 0’5 | Adecuado – 0’5 | Excelente – 1 |
| Claridad en el lenguaje y en el contexto cultural | Adecuado – 0’5 | Bien – 0’75 | Excelente – 1 |
| Coherencia con el currículum | Adecuado – 0’5 | Excelente - 1 | Excelente – 1 |
| Atención a la demanda cognitiva | Bien – 0’75 | Bien – 0’75 | Bien – 0’75 |
| Número apropiado de pasos en la resolución para promover el razonamiento | Baja - 0 | Medio – 0’5 | Alto – 1 |
| Variedad de estrategias de resolución | Un paso – 0 | Múltiples pasos - 1 | Múltiples pasos – 1 |
| Facilitar múltiples soluciones | No – 0 | Sí - 1 | Sí – 1 |
| Oportunidad de éxito | No – 0 | Sí - 1 | Sí – 1 |
| Puntuación total | 2’25/8 | 6,5/8 | 7,75/8 |
A través del análisis de la muestra de los 40 sujetos seleccionados se trató de responder a la pregunta ¿Qué nival de calidad poseen los problemas matemáticos planteados antes y después de recibir formación en PPM?
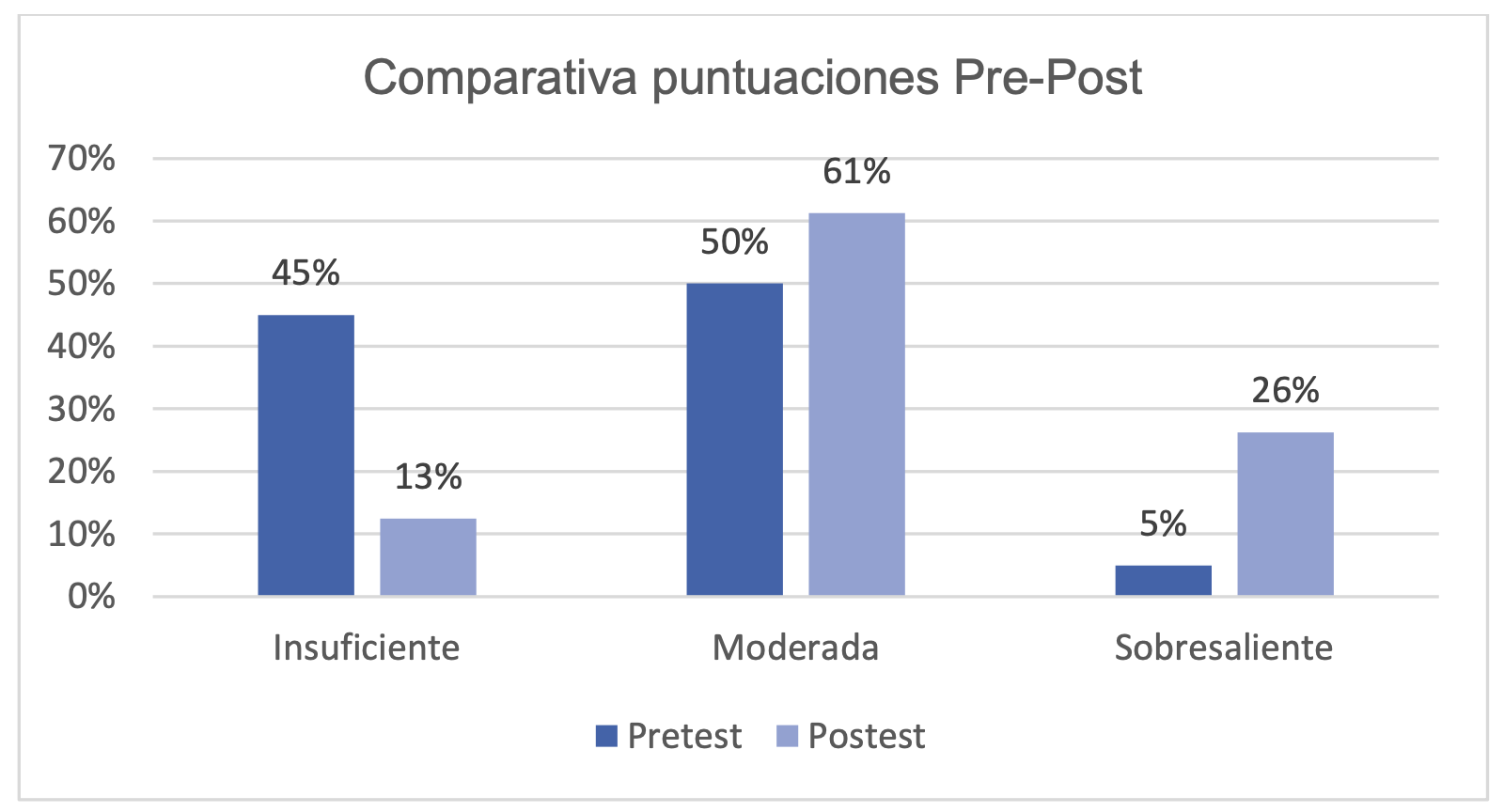
Tal y como muestra la Figura 4, los resultados del pretest indican que la mayoría de los problemas planteados por el profesorado en formación poseen una calidad insuficiente, mientras que solamente el 5% de la muestra planteó un problema de calidad sobresaliente. Así pues, estos datos revelan una gran dificultad a la hora de plantear problemas interesantes matemáticamente, lo que se entiende como una carencia en la habilidad de PPM. Además, las puntuaciones del instrumento F-PosE señalan que los ítems que han obtenido una calificación menor en este primer momento de evaluación han sido “Facilitar múltiples soluciones” y “Atención a la demanda cognitiva”. De esta manera, revelan que las principales causas, que han provocado el planteamiento generalizado de problemas con calidad insuficiente, son la formulación de problemas cerrados que no admiten soluciones alternativas y que no requieren un elevado nivel de esfuerzo cognitivo.
Los resultados del postest indican un aumento en la calidad de los problemas matemáticos con respecto al pretest. De esta manera, la cantidad de problemas de calidad sobresaliente ha crecido hasta alcanzar el cuarto del total de problemas en este segundo momento de evaluación. Por el contrario, solamente 10 de los 80 problemas poseen una calidad insuficiente. Según esto, los ítems que han puntuado más alto en el instrumento F-PosE, y que, por lo tanto, han aportado más a esta visión global son “Variedad de estrategias de resolución” y “Número apropiado de pasos en la resolución para promover el razonamiento”. Igualmente, tras la formación en PPM se ha registrado un aumento en las puntuaciones globales de los ítems “Facilitar múltiples soluciones” y “Atención a la demanda cognitiva” en comparación con las obtenidas en el pretest. De ahí que, tras la formación en PPM, los resultados determinan que el profesorado en formación ha planteado problemas interesantes matemáticamente en los que han tenido en cuenta el proceso de resolución y el tipo de final.
Conclusiones
Tal y como muestra la literatura científica, el PPM es una de las competencias fundamentales que todo docente debe tener. En este artículo se muestra la experiencia al realizar una formación específica en PPM. Con anterioridad a la formación la mayor parte del profesorado en formación no estaba preparado para plantear problemas de calidad, pero se observa un avance muy positivo tras la formación. Estos resultados indican la conveniencia de seguir introduciendo este tipo de formaciones e investigando con muestras más numerosas para afianzar las conclusiones de este estudio.
Referencias
[1] Arce Sánchez, M., Conejo Garrote, L. y Muñoz Escolano, J. M. (2019). Aprendizaje y enseñanza de las matemáticas. Editorial Síntesis.
[2] Brown, S. I. y Walter, M. I. (2005). The art of problem posing. Psychology Press.
[3] Cai, J., y Hwang, S. (2020). Learning to teach through mathematical problem posing: Theoretical considerations, methodology, and directions for future research. International Journal of Educational Research, 102, 101391.
[4] Crespo, S. (2015). A Collection of Problem-Posing Experiences for Prospective Mathematics Teachers that Make a Difference. In: Singer, F., F. Ellerton, N., Cai, J. (eds) Mathematical Problem Posing. Research in Mathematics Education. Springer, New York, NY. DOI.
[5] Crespo, S. y Sinclair, N. (2008). What makes a problem mathematically interesting? Inviting prospective teachers to pose better problems. J Math Teacher Educ 11, 395- 415.
[6] Leavy, A. y Hourigna, M. (2022). The Framework for Posing Elementary Mathematics Problems (F-PosE): Supporting Teachers to Evaluate and Select Problems for Use in Elementary Mathematics. Educational Studies in Mathematics 111, 147-176. DOI.
[7] National Council of Teachers of Mathematics [NCTM]. (1991). Principles and standard for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
[8] National Council of Teachers of Mathematics [NCTM]. (2000). Principles and standard for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
[9] Ortega, T., Pecharromán, C. y Sosa, P. (2011). La importancia de los enunciados de problemas matemáticos. Educatio Siglo XXI, 29(2), 99-116.
[10] Pólya, G. (1945). How to solve it. Uchpedgiz.
[11] Pólya. (1981). Mathematical discovery: On understanding, learning, and teaching problem solving. John Wiley & Sons.
[12] Puig, L. (1996). Elementos de resolución de problemas. Comares.[13] Smith, M. S. y Stein, M. K. (1998). Selecting and creating mathematical tasks: From research to practice. Mathematics Teaching in the Middle School, 3 (5), 344–350.