Diseño e implementación de materiales manipulativos, impresos en 3D, para la mejora de la visualización y estudio de las superficies cuádricas
Resumen
Este estudio explora el uso de modelos tridimensionales impresos en 3D para la enseñanza de superficies cuádricas en la asignatura de Geometría Afín y Métrica del Grado en Matemáticas de la Universitat de les Illes Balears. Los modelos diseñados proporcionan al estudiantado herramientas manipulativas para comprender las propiedades geométricas, promoviendo una mejor visualización e intuición geométrica. La integración de estos recursos en el aula ha mostrado potencial para mejorar la interacción de los estudiantes con conceptos matemáticos abstractos. Las respuestas del estudiantado y del profesorado indican una percepción positiva de la utilidad y aplicabilidad de los modelos en la enseñanza.
Palabras clave
Modelos tridimensionales, superficies cuádricas, Impresión 3D, Visualización geométrica.
Abstract
This study explores the use of 3D printed three-dimensional models for the teaching of quadric surfaces in the course Affine and Metric Geometry of the Degree in Mathematics at the Universitat de les Illes Balears. The models designed provide students with manipulative tools to understand geometric properties, enhancing geometric visualization and intuition. The incorporation of these resources in the classroom has shown potential to improve students’ interaction with abstract mathematical concepts. Students’ and teachers’ responses indicate a positive perception of the usefulness and applicability of the models in teaching.
Keywords
Three-dimensional models, Quadric surfaces, 3D printing, Geometric visualization.
Introducción
La capacidad de visualizar y generar imágenes mentales de objetos tridimensionales es una destreza clave en el estudio avanzado de las matemáticas [1], particularmente en la comprensión de superficies cuádricas y sus propiedades algebraicas. Estos elementos, fundamentales en la geometría afín y métrica, incluyen conceptos como las secciones y las superficies tangentes, que pueden ser abstractos y complejos para el estudiantado. En concreto, la comprensión y la manipulación mental de las estructuras geométricas y sus transformaciones en el espacio puede constituir un obstáculo en el aprendizaje de la materia [2].
En este contexto, la innovación tecnológica ofrece nuevas posibilidades para mejorar la comprensión conceptual a través de recursos didácticos más interactivos, como es el caso del sistema de geometría dinámica GeoGebra. La introducción de modelos geométricos manipulables impresos en 3D, que representan físicamente estas superficies en el espacio, es otro recurso de utilidad para esta mejora. Al disponer de estas formas geométricas tridimensionales, el estudiantado universitario puede tanto visualizar las características que las definen como interactuar directamente con ellas. Esta interacción promueve una comprensión más profunda y significativa de las propiedades geométricas y las expresiones algebraicas que las caracterizan, mejorando así la capacidad del estudiando para resolver problemas en los que intervengan estas figuras [3]. La adaptación de los modelos tridimensionales a las necesidades específicas del currículo de la asignatura de “Geometría afín y métrica” permite una enseñanza más personalizada sobre la que construir los contenidos de la asignatura a partir de un aprendizaje activo basado en la resolución de problemas.
Centrando la atención en las finalidades educativas, este trabajo explora cómo los modelos tridimensionales impresos en 3D pueden ser diseñados y utilizados para facilitar la visualización de las superficies de interés.
Metodología
Selección de Contenidos y Formas Geométricas
Entre las competencias específicas de la asignatura Geometría afín y métrica del grado en Matemáticas de la Universitat de les Illes Balears se encuentra “E5. Clasificar cónicas y cuádricas y resolver problemas relativos a ellas”. Concretamente, se espera que el estudiantado sea capaz de expresar matricialmente la ecuación cuadrática que define una superficie, a la vez que identificar, representar y calcular sus centros, tangentes y asíntotas. De esta forma, y mediante el cálculo de su ecuación en forma normal, el estudiantado podrá comprender la clasificación euclídea de las cónicas y las cuádricas. Con este objetivo en mente, las clases de resolución de problemas son una buena oportunidad para plantear situaciones en las que el estudiantado tenga la “Capacidad de asimilar la definición de un nuevo objeto matemático, en términos de otros conocidos, y ser capaz de utilizar este objeto en diferentes contextos”.
Las figuras tridimensionales seleccionadas para la identificación de estos conceptos son: el hiperboloide de una hoja \((x^{2}+2y^{2}-z^{2}=18)\), el paraboloide hiperbólico \((x^{2}-y^{2}=2z)\), el cilindro parabólico \((x^{2}=2y)\) y el elipsoide \((2x^{2}+y^{2}+z^{2}=25)\). Dicha selección se ha llevado a cabo basándose en los siguientes criterios. Primero, en la diversidad: acotadas y no acotadas, de revolución o no, regladas o no, con y sin centros, cuyas tangentes por puntos exteriores son conos o son dos planos. Segundo, en la facilidad de su expresión algebraica: los coeficientes son números enteros y tienen un tamaño (en centímetros) adecuado para su visualización y medida sobre la impresión 3D. Tercero, en la facilidad de impresión: parametrizadas según el eje que requiere menos soportes. Cuarto, y más importante, en la elaboración conjunta de la actividad: se ha tenido en cuenta desde qué puntos se estudiarían las tangentes, diseñándose conjuntamente tres conos \((0.5x^{2}+0.5y^{2}=z^{2}\), \(0.5x^{2}+y^{2}=z^{2}\), \(2x^{2}+2y^{2}=z^{2})\) que son tangentes a diversas de las figuras en puntos escogidos.
Las dificultades en el estudio de estas superficies tienden a ser de dos tipos: de visualización geométrica y de interpretación de la expresión algebraica que define las superficies cuadráticas y sus superficies tangentes. Del primer tipo, destacamos la interpretación de centro de una superficie (como punto de simetría central que deja invariante la superficie), la identificación de rectas completamente contenidas en cuádricas, y la interpretación geométrica de la superficie tangente (como unión de las rectas tangentes a la superficie que pasan por un punto dado). Del segundo tipo, destaca la expresión de estas mismas rectas mediante ecuaciones matriciales.
Diseño de los Modelos 3D
Existen diferentes herramientas de fácil acceso y uso que permiten el modelado de figuras geométricas tridimensionales a partir de formas primitivas o a partir del uso de la programación por bloques [4]. Estas herramientas pueden ser usadas para la formación en geometría tridimensional desde el alumnado en Educación Primaria hasta estudiantado universitario.
Sin embargo, estas herramientas presentan dificultades para el diseño de modelos más complejos, como las superficies cuádricas. De aquí surge la necesidad de estudiar las posibilidades que ofrece la herramienta OpenSCAD para el diseño detallado de modelos tridimensionales en términos de tamaño, grosor y precisión de la curvatura. OpenSCAD https://openscad.org/ es una herramienta libre de modelado 3D basada en escritura de código que permite utilizar un lenguaje funcional para definir el sólido en el espacio. A diferencia de programas de modelado tridimensional más convencionales que utilizan la manipulación directa de vértices y superficies mediante marcadores de tamaño en un espacio tridimensional, OpenSCAD emplea un enfoque basado en scripts para crear de forma precisa vértices y superficies.
Mediante un script en Python, se han parametrizado puntos de una superficie cuadrática, para después generar los vértices y caras de un polígono que aporta grosor a la superficie. El grosor de la superficie se genera, en cada punto, en la dirección normal a la superficie en ese punto. Se ha utilizado una parametrización de las superficies de la capa inferior a la capa superior optimizado para impresión (resolución eje Z de 0.2mm). Cada capa se ha parametrizado en función de la sección: seno y coseno para elipses, senh y cosh para hipérbolas, y equiespaciadas para rectas y parábolas (resolución ejes X, Y de 0.2mm).
Impresión de los Modelos 3D
La fabricación de los modelos 3D diseñados mediante OpenSCAD se llevó a cabo utilizando tecnología de impresión 3D, elegida por su capacidad para producir objetos complejos y precisos, que son complicados de lograr con otros métodos de producción. Para la fabricación de los modelos, se utilizó filamento tipo PLA (poliácido láctico) mediante la impresora 3D Prusa MK4. Este tipo de filamento es el más habitual y resulta ser un material resistente y de calidad que facilita la manipulación de los modelos por parte del estudiantado en el aula.
Los programas de laminación (o slicer) son utilizados para transformar el modelo elegido para imprimir en las diferentes capas que definirán la figura impresa 3D. En este caso, se puede utilizar el programa de la propia impresora, PrusaSlicer, que ya tiene una configuración predeterminada. Además, el programa, que es gratuito y de código abierto, se puede utilizar con diferentes niveles de configuración y ajuste, permitiendo ajustarse al nivel de conocimientos del usuario.
Durante la impresión de algunos modelos, es necesario implementar el uso de soportes removibles. Estos soportes se utilizan para mantener la estabilidad de las estructuras, especialmente aquellas con voladizos o con ángulos entre capas mayores de 45º, asegurando así la integridad de las formas finales y se generan de forma automática al seleccionar la opción en el programa de laminación. Una vez finalizada la impresión, los soportes son eliminados fácilmente. Habitualmente, durante el proceso de generación de soportes es necesario estudiar diferentes orientaciones de los modelos 3D con el objetivo de reducir el material utilizado en ellos y reducir así el desperdicio. Un ejemplo del uso de soportes se puede observar en la Figura 1 donde se aprecia en verde los soportes generados para poder imprimir el punto de silla correctamente.

Este proceso de optimización de recursos llevó a realizar ajustes en los diseños originales para optimizar el tamaño de los mismos con el fin de reducir material y tiempo de impresión. Se ajustaron las dimensiones de las figuras para que tuvieran como máximo 20 cm de altura. El grosor de la figura se definió para que fuera de 1.6mm. De esta manera, las figuras impresas resultan firmes, finas y de buen tamaño, el suficiente como para que el estudiantado pudiera interactuar cómodamente con ellas y así facilitar la visualización y manipulación.
Implementación en el Aula
La implementación de los modelos 3D se llevó a cabo en una de las clases prácticas en la que se suelen encontrar dificultades en la representación geométrica de los resultados algebraicos derivados del estudio de propiedades de las superficies cuádricas. Para ello, se desarrolló una secuencia de problemas específicos para cada superficie estudiada en la que los modelos 3D podrían ser de utilidad para la exploración y la comprensión de las propiedades y relaciones. Estas actividades estaban diseñadas para ser realizadas mediante trabajo cooperativo y fomentar un aprendizaje participativo, permitiendo a los estudiantes manipular físicamente los modelos mientras aplicaban conceptos teóricos en tiempo real.
En el caso del elipsoide, se le ofreció al alumnado tanto el modelo de la Figura 2 como el acceso a GeoGebra3D donde se podía encontrar el mismo modelo https://www.geogebra.org/m/a8f8yauj. De esta forma, el estudiantado debía responder a las siguientes preguntas:
La intersección entre la cuádrica y los planos \(x=0\), \(y=0\) y \(z=0\) son cónicas. En la referencia dada, ¿qué cónicas se obtienen y cuál es la ecuación de cada una de ellas?
En la referencia dada, ¿Cuál es la ecuación de la cuádrica?
Considera el punto \((4,3,0)^{\mathrm{t}}\). ¿Es de la cuádrica? ¿qué forma geométrica tiene la superficie tangente al punto dado? ¿Cuál es su expresión algebraica?
Considera el punto \((0,0,5)^{\mathrm{t}}\). ¿Es de la cuádrica? ¿qué forma geométrica tiene la superficie tangente al punto dado? ¿Cuál es su expresión algebraica?
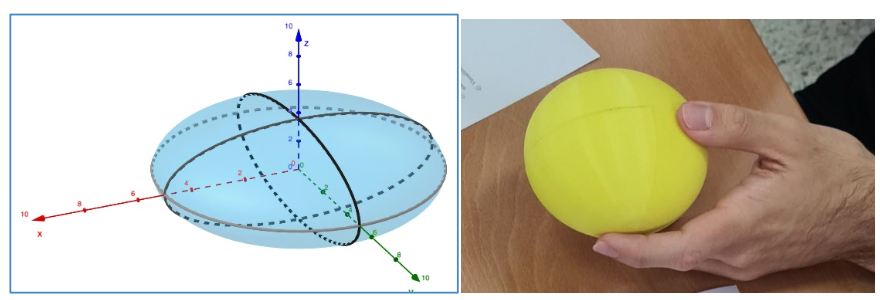
Las preguntas propuestas facilitaban la obtención de la ecuación que definía el elipsoide \((x^{2}+y^{2}+2z^{2}=25)\) y de las superfícies tangentes a los dos puntos estudiadios: el plano tangente \((3x+4y=25)\) al punto \((4,3,0)^{\mathrm{t}}\) y el cono tangente \((-x^{2}-y^{2}+2(z-5)^{2}=0)\) al punto \((0,0,5)^{\mathrm{t}}\).
Evaluación del uso de los modelos 3D
Para medir la efectividad de estos recursos en el proceso de enseñanza se realizó una observación del uso que realizó el estudiantado en la práctica. Adicionalmente, se recopiló retroalimentación tanto de estudiantado como del profesorado respecto a la utilidad y la aplicabilidad de los modelos en el aprendizaje. Esta retroalimentación se obtuvo mediante preguntas abiertas en las fichas de respuesta que buscaban obtener opiniones sobre la experiencia de interactuar con los modelos y la percepción de su valor educativo.
Resultados
En el marco de este estudio, se logró la elaboración de cuatro tipos diferentes de cuádricas (Figura 3) y una colección de conos de tres tipos, diseñados específicamente para actuar como superficies tangentes en los problemas propuestos al estudiantado. Los archivos en formato. scad, con los códigos para la creación de los modelos en OpenSCAD, y. stl, disponibles para la impresión 3D, se encuentran disponibles en la página web: https://github.com/PBibiloni/openscad-quadrics/. Estos modelos, diseñados e impresos en 3D, han sido de utilidad para abordar los conceptos geométricos contemplados en la asignatura.

Las observaciones sobre el uso de estos materiales manipulativos impresos en 3D muestran que, principalmente, se han centrado en promover la intuición geométrica del alumnado. La disponibilidad de estos modelos en el aula facilitó la comprensión de los problemas propuestos, aunque no se encontró una mejora significativa en la habilidad de los estudiantes para responder a los problemas.

La retroalimentación recibida por parte del estudiantado y del profesorado participante evidenció la utilidad de los modelos, destacando la posibilidad de manipularlos e interactuar con ellos, para la mejora de la visualización de las propiedades estudiadas. En concreto, el profesorado destacó cómo los modelos impresos en 3D contribuyeron a una mejor intuición geométrica en la resolución de problemas de su estudiantado. Si bien, una de las estudiantes destacó la utilidad de GeoGebra3D frente a los manipulativos impresos en 3D por la familiaridad con ese software.
Conclusiones
Este estudio exploratorio ha permitido destacar la utilidad de los modelos tridimensionales impresos en 3D en la enseñanza de las superficies cuádricas en la asignatura del Grado en Matemáticas de Geometría Afín y Métrica. Los modelos diseñados han proporcionado al estudiantado recursos tangibles para explorar y comprender propiedades geométricas de las superficies. La implementación de estos modelos en el aula ha permitido promover la intuición geométrica de los estudiantes en la resolución de problemas y una mejor visualización de las superficies cuádricas y sus propiedades.
La retroalimentación recogida de estudiantado y profesorado indica una respuesta positiva hacia la utilidad y aplicabilidad de los modelos en el aula. Los resultados sugieren que la integración de recursos manipulativos impresos en 3D en la enseñanza universitaria puede ser beneficiosa, aunque es necesario realizar un estudio más minucioso. Es recomendable continuar explorando y expandiendo el uso de estas tecnologías en otros campos de las matemáticas, como el análisis matemático. Además, futuras investigaciones podrían enfocarse en comparar la eficacia de los modelos físicos frente a los modelos digitales, como los proporcionados por GeoGebra, para determinar las situaciones en las que cada tipo de modelo es más efectivo.
Al continuar integrando y evaluando los modelos tridimensionales impresos en 3D, podemos avanzar hacia un enfoque más inclusivo, que no solo permita mejorar la intuición geométrica y transformar conceptos abstractos en experiencias tangibles y visuales, sino que también permita aumentar el interés y la motivación del estudiantado.
Referencias
[1] Gutiérrez A. Visualization in 3-dimensional geometry: in search of a framework. Proceedings of the 20th International Conference of the P.M.E., 1, 3-19 (1996).
[2] Clements MA. Origen de las dificultades conceptuales que experimentan en matemática los jóvenes estudiantes. En: Morris R, editor. Estudios en Educación Matemática. Vol. 3. Montevideo: ROSTLA; 1983. pp. 134-162.
[3] Dilling F, Witzke I. The Use of 3D-Printing Technology in Calculus Education: Concept Formation Processes of the Concept of Derivative with Printed Graphs of Functions. Digit Exp Math Educ. 6, 320–339 (2020). Disponible en: https://doi.org/10.1007/s40751-020- 00062-8
[4] Rotger L, Ribera JM, Cuadrado ML. Estrategias inclusivas para la visualización de contenido matemático tridimensional. En: Actas de las III JID+, Jornades d’Innovació Docent en Matemàtiques en Educació Superior; Valencia; 2023. pp. 43–50.