Tejidos de pensamiento
Explorando conceptos matemáticos a través del ganchillo
Resumen
El proyecto TejeMat: Tejemos Matemáticas representa un nuevo enfoque basado en las interacciones. Promueve la colaboración entre disciplinas científicas (las matemáticas) y creativas basadas en el diseño y la artesanía (el ganchillo). La propuesta pretende ayudar a docentes y estudiantes a adentrarse en las matemáticas desde un punto de vista distinto. Ubica el diseño de los trabajos en un espacio límite respecto al conocimiento establecido. Esto aleja a los participantes de la especificidad y los moviliza hacia espacios novedosos e innovadores, hacia la curiosidad, la creación y la exploración. TejeMat es un proyecto que se ha desarrollado durante el curso 23-24 en la Universidad Politécnica de Madrid (UPM). Con su puesta en marcha se ha pretendido acercar, sobre todo a estudiantes, al mundo de las matemáticas y del diseño utilizando el ganchillo como medio de enlace.
Palabras clave
Matemáticas y Ganchillo, Ciencia y Arte, El aprendizaje en y a través de las artes, Metodologías, experiencias y proyectos.
Abstract
The project Tejemat: Tejemos Matemáticas represents a new scope based on the interactions. It promotes the collaboration between scientific (mathematics) and creative disciplines based on the design and the craft (the crocheting). The proposal tries to help teachers and students to meet mathematics from a different point of view. It locates the design of the works in a space that constitute a boundary with respect to the established knowledge. This aparts the participants from the specifity and moves them to fresh and new spaces, to the curiosity, the creation and the exploration. Tejemat is a project developed in the Polytechnic University of Madrid (UPM) in the years 2023-2024. Its start up has pretended to approach to the people, mainly students, to the world of the mathematics and the design by means of the crocheting.
Keywords
Math and Crochet, Science and Art, Learning in and through the arts, Methodologies, Experiences and projects.
Introducción
El ganchillo es una práctica que, en su aparente sencillez, esconde muchas matemáticas. Con este proyecto se propone intensificar su potencialidad como herramienta educativa y motivadora. El ganchillo se relaciona con las matemáticas mediante conceptos que se encuentran implícitos en la forma de hacer este tipo de labores y sus diseños: geometría, polígonos, poliedros, planos hiperbólicos, superficies regladas, espirales, superficie de Lorenz, fractales, teselaciones, series numéricas, proporción áurea, simetrías, etc. Todos ellos pueden ser representados mediante trabajos elaborados con esta técnica. Además, la aritmética también está muy presente: tanto las relaciones de divisibilidad como los múltiplos de un número se utilizan para realizar casi todos los diseños.
Introducir el ganchillo en el saber científico resulta sorprendente y motivador además de que revaloriza esta técnica. Hay que destacar que existen una serie de prejuicios que pueden hacer que el ganchillo no se valore socialmente y menos como herramienta académica. Por ello, con esta propuesta, queremos mostrar los motivos por los que su dimensión matemática queda claramente reflejada.
Consideramos que existen ciertas razones que han actuado negativamente en la consideración de esta técnica:
- Por un lado, al haber sido elaborado mayoritariamente por mujeres, ha sido siempre asociado al ocio propio de ellas.
- Por otro lado, se ha desarrollado casi siempre a nivel privado, en casa y reuniones pequeñas entre aficionadas. Su técnica no ha sido plasmada en libros de carácter científico o educativo.
Actualmente se está produciendo un reconocimiento de la práctica del ganchillo y se está dando a conocer como complemento al aprendizaje [4]. Como ejemplo, se puede destacar que profesores universitarios utilizan esta técnica para explicar y representar conceptos difíciles de transmitir y visualizar de manera “convencional”. Daina Taimina, profesora del Departamento de Matemáticas en la Universidad de Cornell, utiliza en sus clases modelos tejidos con ganchillo para explicar y visualizar la geometría hiperbólica; esta profesora tiene publicados trabajos muy interesantes, uno de ellos premiado [2,6], relacionados con este tema. También existen trabajos publicados que unen ganchillo y teoría del caos. Un ejemplo es el que han llevado a cabo dos profesores de la Universidad de Bristol, Hinke Osinga y Bernd Krauskopf, que han conseguido tejer una representación de la superficie de Lorenz [5]. Otra aplicación de gran impacto ha sido dearrollada por Christine y Margaret Wertheim, fundadoras del Institute For Figuring [8], entidad que contribuye a la comprensión, difusión y divulgación de temas científicos entre cuyas actividades está un proyecto de arte comunitario que ha consistido en la creación de un arrecife de coral tejido con ganchillo (explicando y aplicando técnicas de ganchillo hiperbólico) en el que relacionan matemáticas, arte, ciencias y ecologismo [7]. Ha sido exhibido más de 36 veces en diversos países y ha generado la creación de numerosos arrecifes en distintos lugares. Otros autores trabajan el ganchillo y las superficies topológicas [1,3].
Esta unión de matemáticas y ganchillo ya está haciendo su aparición en centros de Educación Secundaria y forma parte de los programas de actividades de centros tales como el Museum of Mathematics (MoMath) de Nueva York [11], que incluye entre sus actividades cursos de ganchillo topológico, con gran éxito de asistencia.
El ganchillo como herramienta de aprendizaje
Descripción del proyecto
Con el proyecto que hemos desarrollado, TejeMat, se pretende transmitir y extraer el potencial del ganchillo como herramienta educativa transformadora. Impulsar una educación que, además de conocimiento técnico, transmita el trabajo en grupo, la convivencia, la aplicación de los conocimientos al diseño y la creatividad. Que las acciones propuestas ayuden a una educación que enfoque un cambio social. Para todo ello, es muy valiosa la transversalidad que ofrece el ganchillo. Con él se permite el fomento de espacios en los que crear redes entre estudiantes de diversas espacialidades e inquietudes. Pero no solo entre estudiantes, también entre docentes que participan en el proyecto, creando un lugar de encuentro en un ambiente distendido y cooperativo.
Con esta acción, se propone una educación en la que, a través de un taller de varias sesiones, la enseñanza del ganchillo ayude y complemente al aprendizaje de las matemáticas. Donde además de cuestionar los roles y la reproducción de estereotipos en los jóvenes, se fomenten capacidades como la concentración, la memoria, el cálculo numérico, la geometría, etc. La idea es enseñar y aprender matemáticas a través de la manipulación, el diseño y la creatividad, y hacerlo desde una mirada interdisciplinar basada en el disfrute y la recreación.
Desde este nuevo enfoque, el ganchillo se presenta como un saber multidimensional que incorpora un proceso científico (matemático) cuya práctica abarca un amplio abanico de elaboraciones.
Para el buen desarrollo de la propuesta, el grupo ha trabajado junto con la Asociación de Labores Solidarias La IAIA [10] que ha sido la encargada de enseñar la técnica del ganchillo y Katia, marca de manualidades textiles [9], que ha donado todo el material necesario (lanas y agujas).
El proyecto ha seguido la siguiente estructura:
- Publicidad de la propuesta entre los estudiantes y profesores de la UPM.
- Inscripción de los participantes.
- Etapa formativa: una vez inscritos los participantes, se impartieron varias sesiones en las que se combinó el aprendizaje de las técnicas del ganchillo con la presentación y explicación de conceptos matemáticos que podrían ser representados en las creaciones posteriores. Fueron un total de 6 sesiones donde, en la parte dedicada a las matemáticas, se trataron temas relativos a la banda de Möbius, mosaicos, sólidos platónicos, fractales y geometrías no euclidianas.
- Etapa creativa: en ella los participantes se dedicaron a la creación de una propuesta artística sobre algún tema científico abordado durante la etapa formativa o algún otro tema de contenido matemático que despertó interés entre los participantes. En esta fase, que tuvo una duración de cuatro sesiones, estuvieron siempre acompañados por las profesoras de los talleres que les orientaban y aconsejaban.
- Tricotadora social: como final de proyecto, en la última sesión se realizó un taller de tricotado colectivo dinamizado por Elisabeth Lorenzi, profesora de Tecnología Textil de la Escuela Superior de Diseño de Madrid. Entre todos se tejió un cilindro emulando con las manos una tricotadora circular. Esta actividad dio lugar a un encuentro entre alumnos de estudios tecnológicos y alumnos de diseño y moda, trabajando en equipo y generando interacción entre estudiantes de distintas disciplinas.
- La exposición: todas las propuestas han configurado la exposición TejeMat: Tejemos Matemáticas, donde se muestran paneles explicativos y trabajos realizados y que se exhibe en diversos espacios educativos teniendo además una versión virtual.
- Audiovisual: se ha elaborado un vídeo resumen del proyecto que permite difundir el mismo y servir de inspiración para otros.
- Paralelamente se ha creado una página web asociada al proyecto en la que se encuentra toda la información sobre su desarrollo y que alberga la exposición virtual [12].
- Se ha creado una cuenta de Instagram, (@)TejeMat, canal de comunicación actual entre estudiantes, en la que se van publicando imágenes de las sesiones e información relativa al proyecto.
Objetivos
Con las actividades realizadas se ha querido fomentar la importancia del conocimiento multidisciplinar, pero también, del “hacer”, algo que en la Universidad no siempre se tiene en cuenta. Se refuerza la intención de incorporar los saberes de carácter artístico y artesano, en muchas ocasiones considerados solo de las mujeres, a la ciencia. Permiten revindicar la importancia de visibilizar cómo se ha construido el conocimiento, a qué se ha dado valor y a qué no, revalorizando los saberes tradicionalmente femeninos en ocasiones infravalorados.
Dado que los conceptos fundamentales de las matemáticas pueden aprenderse mejor a través de disciplinas creativas y artísticas, estas metodologías activas que incorporan la expresión artística generan emociones positivas que favorecen la actitud hacia el aprendizaje de dichos conceptos.
Con la participación en el proyecto y en las actividades asociadas al mismo, se
han tenido como objetivos principales: - Promover la cultura científica entre los estudiantes, combinando los lenguajes del ganchillo y las matemáticas, dos herramientas directamente relacionadas con la creatividad humana. - Desarrollar en los estudiantes universitarios competencias trasversales de gran valor en su formación. Fomentar en ellos las habilidades sociales y la creatividad a la vez que visualizan la utilidad de algunos de los contenidos que están aprendiendo en la carrera y otros que complementan su formación. - Potenciar otras herramientas, en este caso el ganchillo, como herramienta educativa transformadora. - Cuestionar los roles y la reproducción de estereotipos y fomentar, además, capacidades como la concentración, la memoria y el diseño, así como reforzar conceptos de geometría o de cálculo numérico. - Crear un punto de encuentro entre los docentes y los alumnos universitarios para interrelacionarse, crear y reflexionar sobre la ciencia y su presencia en todas las áreas. - Despertar la conciencia de hábitos y usos responsables de la lana y fibras naturales y trabajar objetivos de desarrollo sostenible que se ajustan a la naturaleza del proyecto: salud y bienestar, educación de calidad, igualdad de género, producción y consumo responsables y alianzas para lograr objetivos.
Las matemáticas del proyecto
Los temas que se han desarrollado en las sesiones teóricas han sido los siguientes:
- Banda de Möbius.
- Mosaicos y teselaciones.
- Fractales.
- Sólidos platónicos.
- Geometrías no euclidianas. Geometría hiperbólica.
Todas las presentaciones utilizadas para la exposición y profundización en estos temas están disponibles en la página web del proyecto [12].
Las sesiones se complementaban con la enseñanza de la técnica del ganchillo: distintos tipos de puntos, aumentos y disminuciones, tejido circular, cuadrado, lectura de patrones, etc., para que los participantes adquiriesen las destrezas necesarias y así poder tejer su proyecto basado en alguno de los conceptos matemáticos trabajados.
Dado que eran proyectos abiertos, la curiosidad de algunos participantes los llevó a tejer otros objetos geométricos tales como la botella de Klein (a la que también se le dedicó un panel explicativo) o las esferas de Dandelin.
Productos resultantes
Con el desarrollo de la propuesta, además de lo comentado en los apartados precedentes, se ha conseguido un material tangible que forma parte de la exposición TejeMat, que está siendo expuesta en diversos centros educativos y culturales. Además, está disponible en la web del proyecto. Aunque la mayoría de los trabajos eran personales, se elaboraron algunas propuestas de forma colaborativa entre todos los participantes, tales como Triángulos de Sierpinski.
Se adjuntan imágenes de algunas de las sesiones realizadas y ejemplos de los proyectos y paneles que forman la exposición (Figuras 1-5).





Valoración de la actividad
El estrecho contacto entre todos los participantes (equipo de trabajo y asistentes) ha permitido un seguimiento directo de actividad, así como de su valoración. No obstante, se ha realizado una encuesta que facilita la evaluación y el conocimiento de las posibles modificaciones que puedan precisarse. La Tabla 1 recoge las preguntas realizadas en dicha encuesta.


Los gráficos de la Figura 7 ilustran los resultados de algunas de las preguntas realizadas en la encuesta.
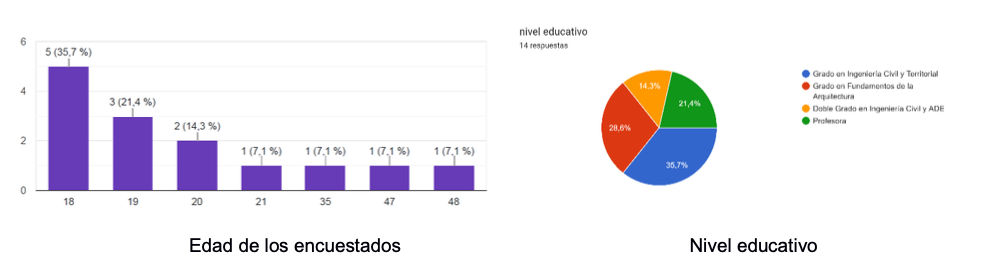
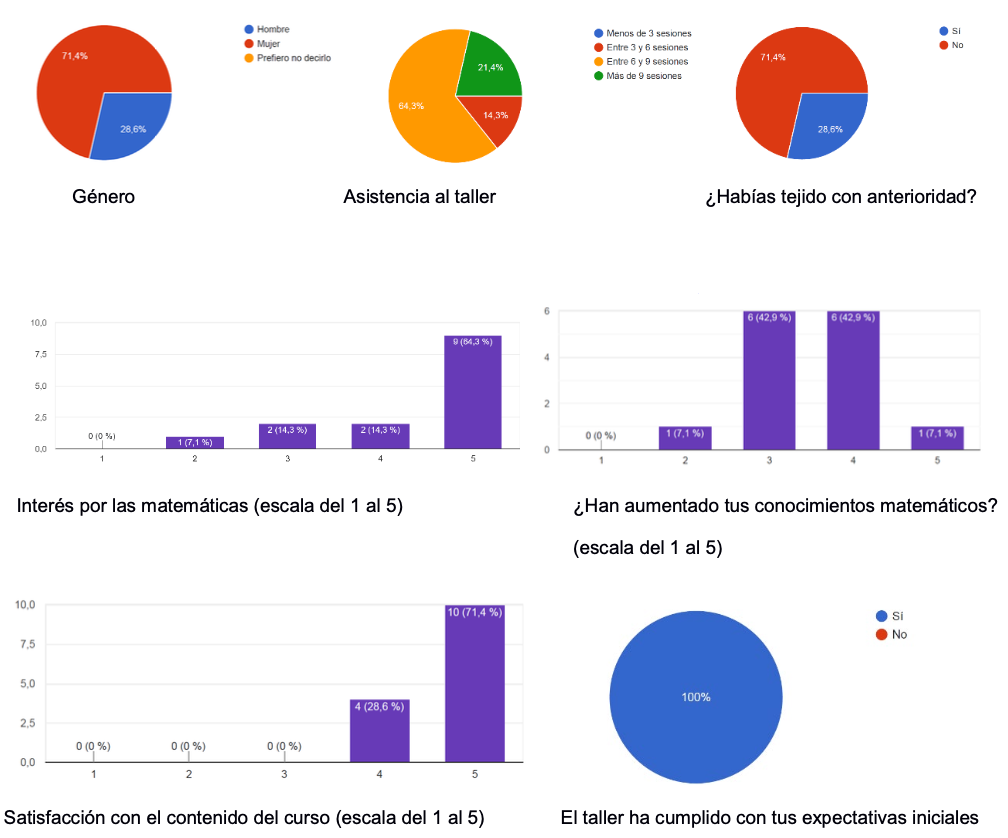
A continuación, se adjuntan también algunos de los comentarios incluidos en la encuesta relativos a ciertas preguntas:
- ¿Qué aspectos del curso has disfrutado más? La compañía, el proyecto final, la gente que he conocido, aprender conceptos básicos que no conocía, las teselaciones y la geometría hiperbólica, el trabajo cooperativo, he aprendido mucho y me he divertido, ser capaz de interpretar patrones y ser capaz de manejarme lo suficientemente bien como para improvisar, la compañía y el ambiente de trabajo también muy agradables, el ambiente del taller.
- ¿Cómo ha influido este taller en tu interés por las matemáticas? Positivamente, me ha motivado a aprender, me ha aclarado conceptos, he visto la relación entre matemáticas y vida cotidiana, ha aumentado mis conocimientos.
- ¿Cómo ha influido este taller en tu interés por el ganchillo? La respuesta casi unánime ha sido que ha despertado gran interés y les ha aficionado a su práctica.
Conclusiones
El contacto directo con los participantes, así como el interés mostrado durante el desarrollo del proyecto y finalmente la buena valoración de la actividad, permite afirmar que con acciones como la realizada se contribuye a:
- Aumentar la participación de los alumnos universitarios en actividades multidisciplinares que contribuyen a generar una opinión crítica.
- Acortar la distancia entre la Ciencia, la Tecnología, la Innovación y el Arte, y los estudiantes. Lograr mejorar la cultura científica de los alumnos.
- Concienciar, formar e informar a los estudiantes sobre la importancia de la conexión entre la Ciencia y el Arte. Fomentar la búsqueda de sinergias y poner en contacto a estas dos ramas que suelen estar muy alejadas.
- Acercar y visibilizar los conceptos técnicos.
- Fomentar el trabajo en común y la relación entre alumnos de diversas formaciones.
- Propiciar que los alumnos se conviertan en agentes principales en la organización de actividades de divulgación científica.
Un video ilustrativo de la actividad puede verse en: 20240131_Tejemat.mp4.
Referencias
[1] Dong, S. Sculpting Mapping Cylinders: Seamless Crochet of Topological Surfaces. Bridges Conference Proceedings, Halifax, Canada, Jul. 26–31, pp. 559–566 (2023).
[2] Henderson, D.W., Taimina, D. Experiencing geometry Euclidean and non-euclidean with history. ISBN: 978-1-4297-9985-0, Pearson Prentince Hall (2020).
[3 Krauskopf, B., Osinga H.M. How to crochet a space-filling pancake: the math, the art and what next Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture (2014).
[4] Martínez Guerrero, A.M. et al. Las matemáticas del ganchillo. XVI Jornadas sobre el aprendizaje y la enseñanza de las matemáticas, Palma (2013).
[5] Osinga, H.M., Krauskopf, B. Crocheting the Lorenz manifold. Mathematical Intelligencer, 26(4), 25-37 (2004).
[6] Taimina, D., Crocheting adventures with hyperbolic plane, CRC Press. (2009).
[9] Katia, marca de manualidades textiles.
[10] La IAIA
[11] National Museum of Mathematics
[12] TejeMat; 20240131_Tejemat.mp4