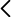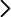Zonas de Brillouin de las estructuras cúbica simple, centrada en caras y centrada en cuerpo

Categories:

Física quàntica, estructura de la matèria i estat sòlid.

Autors:

ana cros stotter

Etiquetes:

cristalografía, geometría, física del estado sólido.

Objectius:

Entender las características geométricas de la primera zona de Brillouin de las redes de Bravais cúbicas.

Materials:

Estructuras de papel ya montadas.

Descripció:

En esta demostración se utilizan varias estructuras geométricas que representan la primera zona de Brillouin de las redes de Bravais cúbicas: cúbica simple (sc), cúbica centrada en caras (fcc) y cúbica centrada en cuerpo (bcc).

Procedimiento

Se muestran las estructuras tridimensionales y su relación con la celda unidad cúbica correspondiente del espacio recíproco. Las figuras se pueden manipular, apilar, e inscribir en el cubo. Su volumen puede compararse directamente, puesto que están diseñadas de forma que se inscriban en el mismo cubo.

Explicación

La relación básica entre los vectores que generan la red directa de una red de Bravais, a_i, con los que generan su red recíproca, g_i, viene dada por:

$a_{i}\cdot g_{i}=2\pi \delta _{ij}$

La zona de Brillouin se define como la celda de Wigner-Seitz de la red recíproca. Para encontrar esta celda se establece el origen en un punto de red y se dibujan vectores desde el origen a todos los primeros vecinos. Los planos que bisectan estos vectores delimitan la celda de Wigner-Seitz (primera zona de Brillouin si se trata de la red recíproca).

La red recíproca de una red cúbica simple (sc) de parámetro de red a es otra red cúbica simple de parámetro de red 2 $\pi$ /a. La primera zona de Brillouin es un cubo de arista 2 $\pi$ /a.

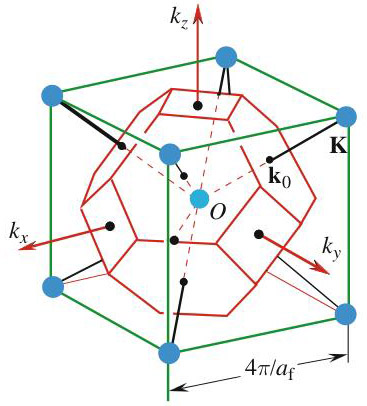
Como se muestra en la Fig. 1, la red recíproca de una red bcc con parámetro de red a_b (es decir, cuya celda unidad cúbica tiene una arista a_b) es una red fcc de parámetro de red 4 $\pi$ /a_b. La primera zona de Brillouin corresponde a un dodecaedro rómbico (o rombododecaedro) inscrito en el cubo. En el centro de este cubo y en el centro de cada una de sus aristas se encuentra un punto de la red fcc. La arista del cubo vale 4 $\pi$ /a. El volumen de la primera zona de Brillouin es 1/4∙(4 $\pi$ /a_b)³=2(2 $\pi$ /a_b)³. Una forma de visualizar esta relación consiste en apilar los rombododecaedros verdes alrededor del rombododecaedro color naranja.


Fig. 1: Izquierda: primera zona de Brillouin de la red bcc, imagen obtenida de: http://ruby.chemie.uni-freiburg.de/Vorlesung/intermetallische_2_3.html. La red recíproca es fcc con parámetro 4 $\pi$ /a_b (rombododecaedro). Centro: seis rombododecaedros verdes dispuestos alrededor del rombododecaedro central, mostrando cómo llenan el espacio al apilarse. Derecha: rombododecaedro inscrito en un cubo mostrando los puntos de alta simetría.

Imaginando el rombododecaedro central inscrito en un cubo, alrededor tiene 12 rombododecaedros y ¼ de cada uno de ellos se encuentra en el interior de ese cubo. Por lo tanto, el volumen del cubo será el del rombododecaedro central, más el volumen de 12/4=3 rombododecaedros más, es decir, cuatro veces el volumen de la zona de Brillouin. Para mayor claridad, puede probarse cómo el rombododecaedro naranja se inscribe en el cubo semitransparente, como se muestra en la figura 3, derecha.


Fig. 2: Izquierda: Primera zona de Brillouin de la red bcc con indicación de los puntos de alta simetría. Imagen extraída De http://ruby.chemie.uni-freiburg.de/Vorlesung/intermetallische_2_3.html .Derecha: modelo en papel de la primera zona de Brillouin de la red bcc, con indicación de los puntos de alta simetría que hay en su superficie.

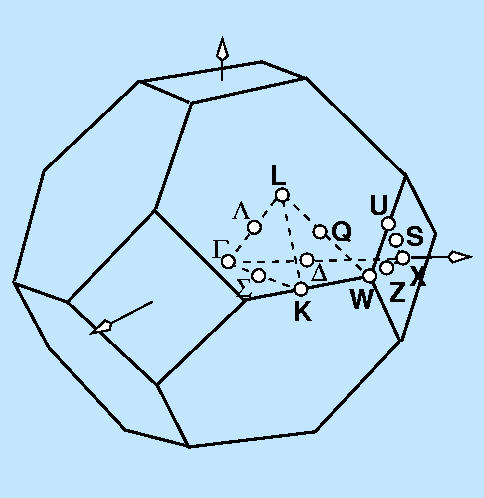
La figura 2 muestra el detalle de los puntos de alta simetría. En el modelo de papel se muestran únicamente los que se encuentran en la superficie de la figura.

Como se muestra en la Fig. 3, la red recíproca de una red fcc con parámetro de red a_f (es decir, cuya celda unidad cúbica tiene una arista a_b) es una red bcc de parámetro de red 4p/a_f. La primera zona de Brillouin corresponde a un octaedro truncado inscrito en el cubo. En el centro de este cubo y en el centro de cada una de sus caras se encuentra un punto de la red bcc. La arista del cubo vale 4 $\pi$ /a. El volumen de la primera zona de Brillouin es 1/2∙(4 $\pi$ /a_b)³=4(2 $\pi$ /a_b)³. Una forma de visualizar cómo cubre el espacio consiste en apilar las figuras azules en torno a la de color naranja.


Fig. 3: Izquierda: primera zona de Brillouin de la red fcc, imagen obtenida de: http://ruby.chemie.uni-freiburg.de/Vorlesung/intermetallische_2_3.html. La red recíproca es bcc con parámetro 4 $\pi$ /a_f (octaedro truncado). Centro: tres octaedros truncados azules dispuestos alrededor del central, mostrando cómo llenan el espacio al apilarse. Derecha: octaedro truncado inscrito en un cubo.

Finalmente, la figura 4 muestra la localización de los puntos de alta simetría que han podido dibujarse sobre la arista del octaedro truncado.


Fig. 4: Izquierda: Primera zona de Brillouin de la red bcc con indicación de los puntos de alta simetría. Imagen extraída de http://ruby.chemie.uni-freiburg.de/Vorlesung/intermetallische_2_3.html. Derecha: modelo en papel de la primera zona de Brillouin de la red bcc, con indicación de los puntos de alta simetría que hay en su superficie.

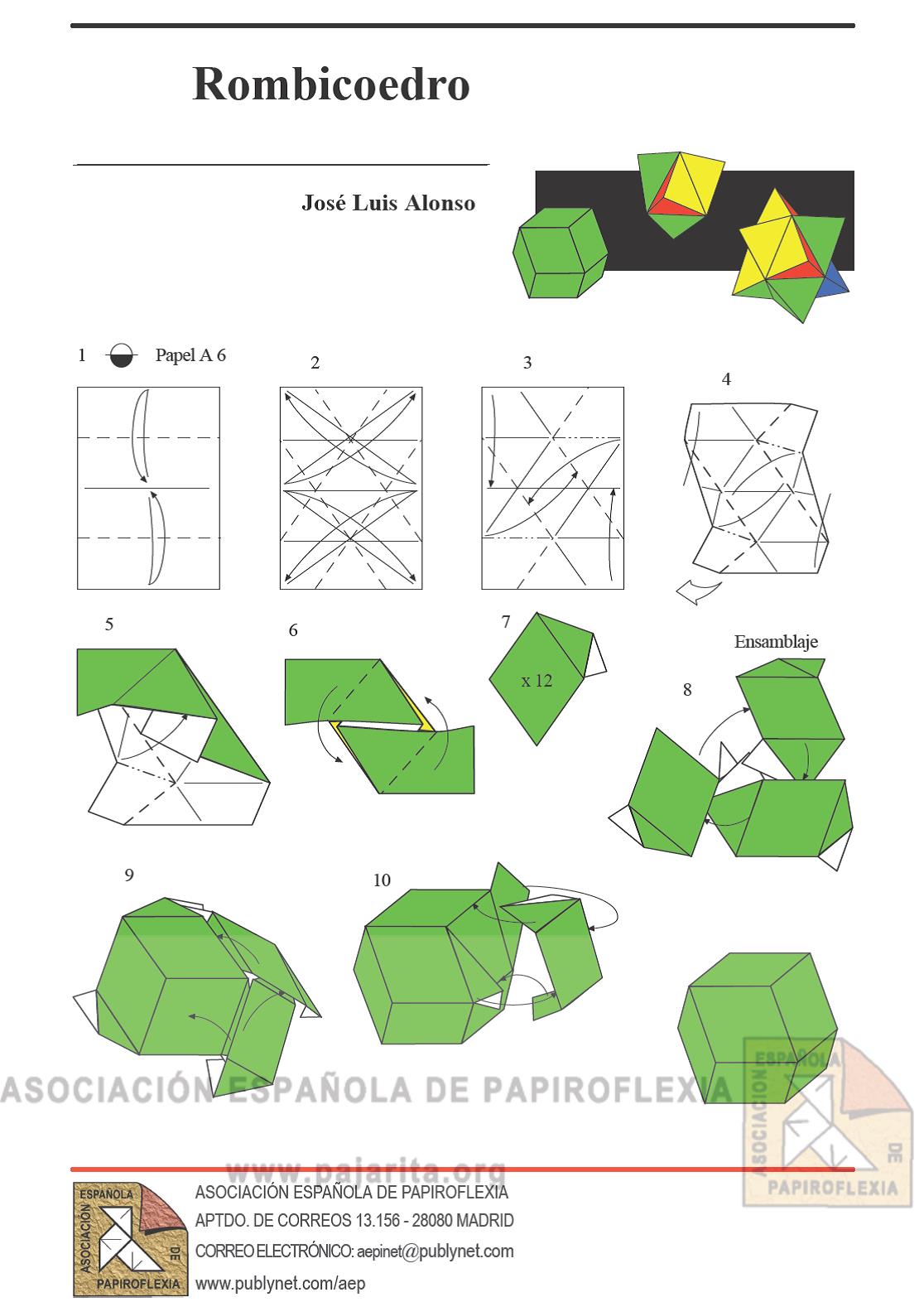
Instrucciones para realizar las piezas mediante papiroflexia modular:

Rombododecaedro:

Zonas de Brillouin de las estructuras cúbica simple, centrada en caras y centrada en cuerpo Para realizarlos a escala se han utilizado las siguientes medidas:

Cubo de plástico de arista 10.5 cm.

Rombododecaedro: Cada pieza se realiza con un papel de 10.5x14.8 cm

Octaedro truncado: cada pieza se realiza con un papel de 5x5 cm

Bibliografia:

T. Wada, Heat storage capacity of sodium acetate trihydrate during thermal cycling, Solar Energy 33 (1984) 373-375.
B. Sandnes, The physics and chemistry of the heat pad, Am. J. Phys. 76 (2008) 546.
J. B. Berg et alt., Thermal conductivity enhancement of sodium acetate trihydrate by adding graphite powder and the effect on stability of supercooling, Energy Procedia, 70 (2015) 249-256.

Galeria de vídeos:

Octaedro truncado

Fitxa:

Demo 155 en pdf