Cards and card holders

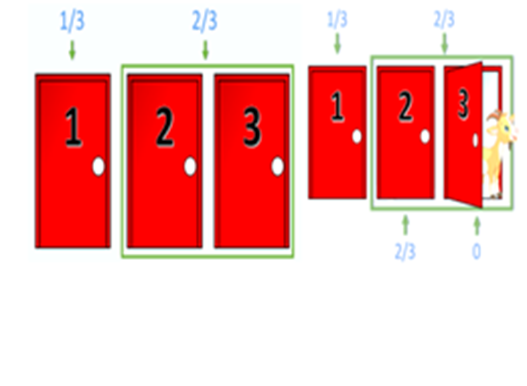
The Monty Hall problem is a famous mathematical probability dilemma based on a hypothetical scenario inspired by the American TV quiz show “Let's Make a Deal”. The situation is as follows: Imagine you are in a quiz show and you have to choose between three locked doors. Behind one of them there is a car and behind the other two there are goats (as an example of a worthless prize). You choose a door, for example, number 1. The presenter, who knows what is behind each door, opens another door, say number 3, always revealing a goat (i.e. the only door with a goat if the one you have chosen hides a goat or a random one between the two possibilities if you have chosen the car door). It then offers you the opportunity to change your initial choice to the other locked door, number 2. The question is: Should you keep your original choice or switch to the other door? Do your odds of winning the car increase if you switch doors? The (to some) counterintuitive answer is that yes you should switch doors. At first, the probability that the car will be behind the door you chose is 1/3, and the probability that it will be behind one of the other two doors is 2/3. When the presenter opens a door that has a goat, the probability of 2/3 does not change, but now concentrates on the one door that remains closed. Therefore, changing doors doubles your chances of winning the car to 2/3. This problem has generated much debate and confusion because it defies many people's intuition, but mathematically, switching doors is the strategy that maximizes your chances of winning [1]. In this demonstration we propose to perform the experiment repeatedly to show which strategy is the best by accumulating enough statistics. There are also websites where such a simulation can be done [2]. Many people reason that it makes no difference whether to switch or not, since the probability of being right is 50% for each one, but that would only be true for the case in which the player chooses after opening one of the doors.

In order to be able to perform many tests on the spot, three laminated cards are used which can be placed on supports (those numbered from 1 to 3). On each card there is a door on one side and a car or a goat on the other. There are more cards with goats for a test that will be explained later. The procedure is as follows:

1) A “secretary” is elected who will go to the blackboard to write down the results (i.e., if each student-contestant takes the car or not). 2) Students are asked if they would keep the initial door, if they would change or if they think it doesn't matter. Two groups are made, one with those who would change and the other with those who would not change or think it doesn't matter. Alternatively, those who think it is all the same can be included in the other group if this results in groups that are more even in number. This classification is done previously to avoid that, as they see what the previous classmates choose or the result of the tests, they all end up choosing the same thing. 3) The quiz is carried out with each of the students (first for one of the previous groups, then for the other, to facilitate the counting by the secretary). For each quiz the teacher shuffles the cards, placing them in the holder so that they show the students the doors. The student chooses one door, the teacher “opens” one of the other two that does not have a goat, and the student changes his choice or not depending on whether he has chosen to be in the group of those who change or not. The secretary notes whether or not he/she is correct with his/her final “choice”. 4) To ensure that there are sufficient statistics, several rounds can be done for each of the groups, so that at the end there are at least 30 cases in both groups, better if there are 40. In that case it is more evident that if we choose a door at random and the presenter opens 8 doors with no prize, the most reasonable thing to do is to change doors because clearly the probability of having been right in our first choice is very low (10%). This test can be performed with the additional holders and cards (there is also an extra replacement card).

It can be commented that it is a problem that is mentioned in several elements of popular culture, for example: The problem was popularized by Marilyn vos Savant in her column in Parade Magazine in 1990, which led to a wide public debate about the correct solution. This story is mentioned in the novel “The Curious Incident of the Dog at Midnight” by M. Haddon. It also appears in the movie “21 blackjack”, directed by R. Luketic, or in episodes of the series Friends, Brooklyn Nine-Nine or The Hollow.

[1] https://es.wikipedia.org/wiki/Problema_de_Monty_Hall [2] https://www.mathwarehouse.com/monty-hall-simulation-online/