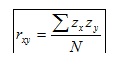
El fonament del coeficient de Pearson és el següent: com més intensa siga la concordança (en sentit directe o invers) de les posicions relatives de les dades en les dues variables, el producte del numerador presenta major magnitud (en sentit absolut, llevat el signe). Si la concordança és exacta, el numerador és igual que N (o que -N) i, en conseqüència, l'índex és d'1 (o -1).

Exemple 1 (Màxima covariació positiva)

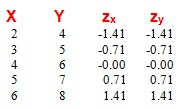
Observeu que les dades tipificades (transformades com a puntuacions z) en les dues columnes de la dreta tenen els mateixos valors en les variables, donat que les posicions relatives són les mateixes en les variables X i Y.

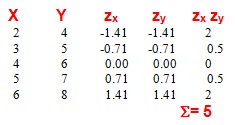
Si obtenim els productes dels valors tipificats per cada cas, el resultat és:

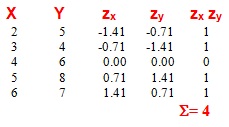
El quocient de dividir la suma de productes (5) per N (cal tenir en compte que N és el nombre de casos i NO, el nombre de dades) és 1:

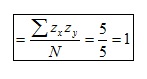
Exemple 2 (Covariació positiva d'alta intensitat)

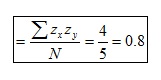
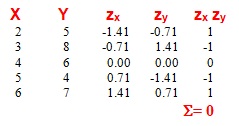
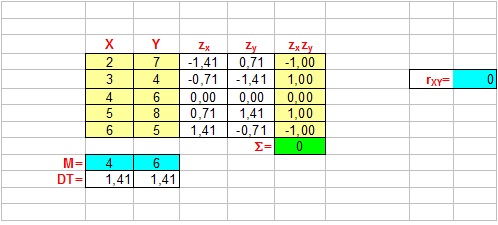
Exemple 3 (Absència de covariació)

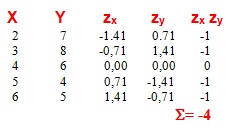
Exemple 4 (Covariació negativa d'alta intensitat)

Exemple 5 (Màxima covariació negativa)

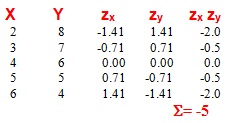
El valor de la correlació és igual que 1 o -1 si la covariació és d'intensitat màxima i aproxima el 0 com més baixa siga la intensitat de la covariació. A més, l'índex pren signe positiu si la covariació és directa, i negatiu, si és inversa.

Característiques

a) El coeficient de correlació de Pearson pren valors entre -1 i 1.

b) La correlació d'una variable en ella mateixa sempre és 1.

c) El valor 0 indica absència de covariació lineal, llevat que la covariació siga de tipus no lineal. (Vegeu l'exemple en l'apartat de relacions no lineals.)