Una forma senzilla de quantificar l'error de predicció consisteix en obtenir les diferències entre els valores predits i els valores reals:

on:

e: error de predicció o estimació

Y: valor reals de la variable que volem estimar

Y': predicció o estimació

Exemple:

Si les mesures reals de sensació de malestar dels pacients que han fet 1 i 7 sessions de teràpia són 4.6 i 3.1 respectivament, tenim que en les prediccions obtingudes amb la primera equació hem comés una errada la magnitud de la qual és 1 per a X=1, i 0 per X=7. En les prediccions obtingudes amb la segona equació, les errades són iguals a 0 i -0.3 respectivament:

(Y'₁ i Y'₂ simbolitzen les puntuacions estimades amb la primera i segona equació respectivament).

Sembla clar que hi ha menys error de predicció amb la segona equació, i per tant és preferible a la primera. No obstant això, devem tindre en compte la resta de casos, i resulta:

(e₁ i e₂ son els errors d'estimació amb les equacions 1 i 2 respectivament)

Les sumes de diferències entre puntuacions reals i estimades (columnes amb símbol e) són, respectivament 4.2 i 1.5 per a cada equació. Però observem que algunes diferències a la columna de la dreta són negatives. En conseqüència les sumes NO mesuren correctament la magnitud de l'error, i per esta raó treballem en les sumes de quadrats de les errades per tal de eliminar els signes negatius, i direm que l'error de predicció és quantificat segons el criteri de mínims quadrats:

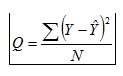
Nota:

a) Els símbols més utilitzats per a les puntuacions estimades son Y' o el que està posat a la fórmula.

b) La suma de quadrats d'errors es divideix per N per tal de fer possible comparacions entre conjunts de dades de grandària diferent.