Las hipótesis son proposiciones verificables respecto de características de interés. Ejemplo: "La nueva terapia mejora el estado de los pacientes con ansiedad". Las hipótesis estadísticas asignan valores a los parámetros poblacionales. Ejemplo: "la nueva terapia mejora la proporción de pacientes curados en un 20%".

La hipótesis inicial es denominada Hipótesis Nula, y se acompaña de las Hipótesis Alternativas, que asignan valores al parámetro para el caso de que rechacemos la Hipótesis Nula. La Hipótesis Nula es un supuesto provisional sobre las características de la población a que pertenece la muestra (o las muestras de haber más de una).

Las Hipótesis Nula y Alternativa son simbolizadas de la siguiente forma:

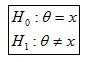
donde

Ejemplo

Queremos saber si una moneda tiene sesgo (una moneda sesgada es aquella en que las probabilidades de "cara" y "cruz" son diferentes). La Hipótesis Nula asume que la moneda es insesgada (1) y por tanto la proporción de "caras" es idéntica a la de "cruces" (0.5), y se expresa de la siguiente forma:

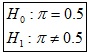
donde p es la proporción de "caras" que observaríamos si lanzáramos la moneda gran número de veces (teóricamente, un número infinito).

(1) Generalmente las Hipótesis Nulas se enuncian bajo el supuesto de que no hay efectos, por ejemplo, de que las muestras observadas pertenecen a las poblaciones definidas en las Hipótesis Nulas, no hay diferencias estadísticas entre las muestras comparadas, correlaciones nulas, etc., y en el ejemplo ausencia de efectos significativos significa que la moneda es insesgada. No debe confundirse las Hipótesis Nulas con las hipótesis del investigador, que habitualmente analiza los datos para hallar efectos significativos.