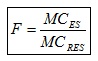El análisis de Varianza intrasujetos contrasta la hipótesis de igualdades de las Medias de muestras recogidas en los mismos sujetos. Ejemplo: Queremos probar si una bebida tiene efecto estimulante, y damos a beber una dosis pequeña (0,5dl.) a un grupo de individuos seleccionados aleatoriamente. A las 24 horas les damos una dosis de 1dl., y hacemos lo mismo durante los dos días siguientes en dosis de 1,5 y 2dl. Cada día, al acabar de beber los administramos una prueba de coordinación motora, y recogemos los siguientes datos:

El análisis de los datos de grupos relacionados presenta características específicas: Cada fila define un grupo de datos del mismo sujeto. En consecuencia, la MC_I no es un estimador adecuado de la variación aleatoria porque los datos no son independientes. Por otro lado, parte de la variación observada entre columnas es explicada por el efecto de los tratamientos (si hay efecto). Por esta razón la variación entre las filas (que es variación entre sujetos) mide la variación ocasionada por diferencias entre tratamientos más la variación ocasionada por diferencias individuales entre sujetos.

Para resolver el problema, se define la variación aleatoria como el residuo de sustraer la variación "entre tratamientos" y la variación "entre sujetos" de la variación total:

La prueba F tiene el mismo sentido que en el Análisis de Varianza intersujetos, pero se hacen poniendo en el numerador la Media Cuadrática que corresponda y en el denominador la Media Cuadrática residual.

Prueba F para someter a contraste la Hipótesis Nula de que los tratamientos no son efectivos:

Prueba F para someter a contraste que la variación ocasionada por diferencias individuales es nula: