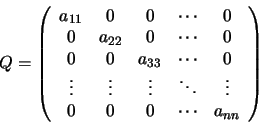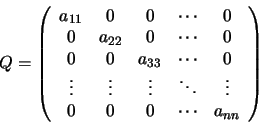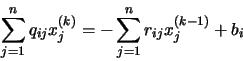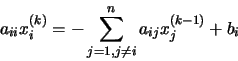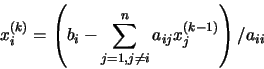6.2.3 Método de Jacobi

En la iteración de Jacobi, se escoge una matriz Q que es diagonal y cuyos elementos diagonales son los mismos que los de la matriz A. La matriz Q toma la forma:

$$Q= \left( \begin{array}{ccccc} a_{11} & 0 & 0 & \cdots & 0 ... ...& \vdots \\ 0 & 0 & 0 & \cdots & a_{nn} \end{array} \right)$$

y la ecuación general (63) se puede escribir como

 

Qx^(k) = (Q-A)x^(k-1) + b (65)

Si denominamos R a la matriz A-Q:

$$R= \left( \begin{array}{ccccc} 0 & a_{12} & a_{13} & \cdots... ...\ a_{n1} & a_{n2} & a_{n3} & \cdots & 0 \end{array} \right)$$

la ecuación (65) se puede reescribir como:

Qx^(k) = -Rx^(k-1) + b

El producto de la matriz Q por el vector columna x^(k) será un vector columna. De modo análogo, el producto de la matriz R por el vector columna x^(k-1) será también un vector columna. La expresión anterior, que es una ecuación vectorial, se puede expresar por necuaciones escalares (una para cada componente del vector). De este modo, podemos escribir, para un elemento i cualquiera y teniendo en cuenta que se trata de un producto matriz-vector:

$$\sum_{j=1}^{n} q_{ij}x_{j}^{(k)} = - \sum_{j=1}^{n} r_{ij}x_{j}^{(k-1)} + b_{i}$$

Si tenemos en cuenta que en la matriz Q todos los elementos fuera de la diagonal son cero, en el primer miembro el único término no nulo del sumatorio es el que contiene el elemento diagonal q_ii, que es precisamente a_ii. Más aún, los elementos de la diagonal de Rson cero, por lo que podemos eliminar el término i=j en el sumatorio del segundo miembro. De acuerdo con lo dicho, la expresión anterior se puede reescribir como:

$$a_{ii}x_{i}^{(k)} = - \sum_{j=1, j \neq i}^{n} a_{ij}x_{j}^{(k-1)} + b_{i}$$

de donde despejando x_i^(k) obtenemos:

$$x_{i}^{(k)} = \left( b_{i} - \sum_{j=1, j \neq i}^{n} a_{ij}x_{j}^{(k-1)} \right) / a_{ii}$$

que es la expresión que nos proporciona las nuevas componentes del vector x^(k) en función de vector anterior x^(k-1) en la iteración de Jacobi. En la figura (14) se presenta un algoritmo para el método de Jacobi.

  

Figure: Implementación del método de Jacobi.

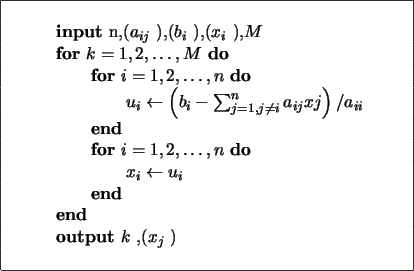El método de Jacobi se basa en escribir el sistema de ecuaciones en la forma:

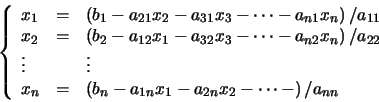$$\left\{ \begin{array}{lll} x_{1} & = & \left( b_{1} - a_{2... ...2n}x_{2} - \cdots - \right) / a_{nn} \\ \end{array} \right.$$ (66)

Partimos de una aproximación inicial para las soluciones al sistema de ecuaciones y sustituimos estos valores en la ecuación (66). De esta forma, se genera una nueva aproximación a la solución del sistema, que en determinadas condiciones, es mejor que la aproximación inicial. Esta nueva aproximación se puede sustituir de nuevo en la parte derecha de la ecuación (66) y así sucesivamente hasta obtener la convergencia.