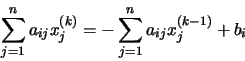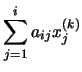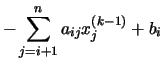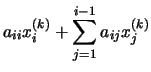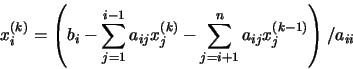Next: 7. Interpolación
Up: 6.2 Métodos iterativos
Previous: 6.2.3 Método de Jacobi
La iteración de Gauss-Seidel se define al tomar Q como la
parte triangular inferior de A incluyendo los elementos de la
diagonal:
Si, como en el caso anterior, definimos la matriz R=A-Q
y la ecuación (63) se puede escribir en la forma:
Qx(k) = -Rx(k-1) + b
Un elemento cualquiera, i, del vector Qx(k) vendrá dado por la
ecuación:
Si tenemos en cuenta la peculiar forma de las matrices Q y R,
resulta que todos los sumandos para los que j > i en la parte
izquierda son nulos, mientras que en la parte derecha son nulos todos los
sumandos para los que 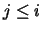 .
Podemos escribir entonces:
.
Podemos escribir entonces:
de donde despejando
xi(k), obtenemos:
Obsérvese que en el método de Gauss-Seidel los valores actualizados de
xi sustituyen de inmediato a los valores anteriores, mientras que
en el método de Jacobi todas las componentes nuevas del vector se
calculan antes de llevar a cabo la sustitución. Por contra, en el
método de Gauss-Seidel los cálculos deben llevarse a cabo por orden,
ya que el nuevo valor xi depende de los valores actualizados de
x1, x2, ..., xi-1.
En la figura (15) se incluye un algoritmo para la
iteración de Gauss-Seidel.
Figure:
Algoritmo para la iteración de Gauss-Seidel.
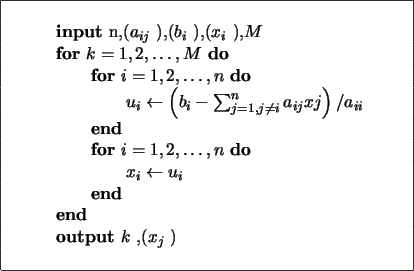 |



Next: 7. Interpolación
Up: 6.2 Métodos iterativos
Previous: 6.2.3 Método de Jacobi
Wladimiro Diaz Villanueva
1998-05-11