 En
el siglo III a.C. una colonia griega al sur de Italia, Thurii, se
alió
con Roma para defenderse de las tribus italianas vecinas. Al cabo de un
tiempo, Tarento, otra colonia griega, consideró insultante
que sus compatriotas recurrieran a la ayuda de unos bárbaros
para
defenderse, así que capturaron una nave romana, mataron a su
capitán,
marcharon sobre Thurii y expulsaron a los romanos. Roma tenía
entonces
otros problemas, y decidió enviar un embajador y arreglar
pacíficamente
el incidente. Pero los Tarentinos encontraron al enviado
particularmente
"gracioso", especialmente por su forma de hablar griego. No se lo
tomaron
en serio, hasta el punto de que alguien entre la gente que observaba al
bárbaro, tuvo a bien mear sobre su túnica. El embajador
se
marcho jurando que lavarían la mancha con sangre, y así
el
año 281 a.C. el senado romano declaró la guerra con
la que Roma se anexionó el sur de Italia. No podemos saber
qué
les pareció tan hilarante a los griegos del lenguaje del
embajador,
pero no es difícil hacer ciertas conjeturas: el griego
tenía
sonidos de los que carecía el latín, por lo que es
probable
que sonara bastante palurdo oír llamar thetas a las zetas, por
ejemplo,
o chis (más probablemente kis) a las jis, mus a las mys y cosas
parecidas. No pensemos ya lo que habría pasado si el pobre
embajador
hubiera confundido las fis con las sigmas, como hacen hoy más
matemáticos
de los que podría esperarse. No cuesta más de media hora
aprenderse esto:
En
el siglo III a.C. una colonia griega al sur de Italia, Thurii, se
alió
con Roma para defenderse de las tribus italianas vecinas. Al cabo de un
tiempo, Tarento, otra colonia griega, consideró insultante
que sus compatriotas recurrieran a la ayuda de unos bárbaros
para
defenderse, así que capturaron una nave romana, mataron a su
capitán,
marcharon sobre Thurii y expulsaron a los romanos. Roma tenía
entonces
otros problemas, y decidió enviar un embajador y arreglar
pacíficamente
el incidente. Pero los Tarentinos encontraron al enviado
particularmente
"gracioso", especialmente por su forma de hablar griego. No se lo
tomaron
en serio, hasta el punto de que alguien entre la gente que observaba al
bárbaro, tuvo a bien mear sobre su túnica. El embajador
se
marcho jurando que lavarían la mancha con sangre, y así
el
año 281 a.C. el senado romano declaró la guerra con
la que Roma se anexionó el sur de Italia. No podemos saber
qué
les pareció tan hilarante a los griegos del lenguaje del
embajador,
pero no es difícil hacer ciertas conjeturas: el griego
tenía
sonidos de los que carecía el latín, por lo que es
probable
que sonara bastante palurdo oír llamar thetas a las zetas, por
ejemplo,
o chis (más probablemente kis) a las jis, mus a las mys y cosas
parecidas. No pensemos ya lo que habría pasado si el pobre
embajador
hubiera confundido las fis con las sigmas, como hacen hoy más
matemáticos
de los que podría esperarse. No cuesta más de media hora
aprenderse esto:
 Es conocida la frase
"Te ayudaré a recordar la
cantidad", que al contarle las letras nos ayuda a recordar la
cantidad e = 2,71828...
Una frase para pi = 3,1415926535...
es "Sol y Luna y Cielo proclaman al Divino
autor del Mundo". Hay ejemplos más sofisticados, como
este poema de Manuel Golmayo:
Es conocida la frase
"Te ayudaré a recordar la
cantidad", que al contarle las letras nos ayuda a recordar la
cantidad e = 2,71828...
Una frase para pi = 3,1415926535...
es "Sol y Luna y Cielo proclaman al Divino
autor del Mundo". Hay ejemplos más sofisticados, como
este poema de Manuel Golmayo:Soy y seré a todos definible;
mi nombre tengo que daros:
cociente diametral siempre inmedible
soy, de los redondos aros.
Nos da la aproximación pi = 3,1415926535897932384... con 20 decimales. Tengo una prueba (anónima, no recuerdo de dónde la saqué) relativamente simple (más algebraica que analítica) de la trascendencia de e y pi. Puedes bajártela desde aquí.
Aprovecho este rincón para plantear un problema muy simple: determinar el criterio que ordena como sigue la sucesión de los primeros números naturales:
0
5 4 2 9 8
6 7 3 1
La
solución cabe en dos palabras (cuatro si no queremos ser
lacónicos).Todas las mujeres tienen los ojos azules
QED
UN
SILOGISMO DE
LEWIS CARROLL
 He aquí un encantador silogismo sacado
de "El juego de la
lógica",
de Lewis Carroll. Su encanto radica en lo sutil de la falacia:
He aquí un encantador silogismo sacado
de "El juego de la
lógica",
de Lewis Carroll. Su encanto radica en lo sutil de la falacia:- Nadie que quiera tomar el tren y que no pueda coger un taxi y que no tenga tiempo suficiente para ir dando un paseo hasta la estación, puede tomarlo sin echar a correr.
- Este grupo de turistas quiere tomar el tren y no puede coger
un taxi, pero les sobra tiempo para ir hasta la estación dando
un paseo.
Por consiguiente: - Este grupo de turistas no necesita correr.
EL
SILOGISMO FAVORITO DE RAYMOND SMULLYAN
Raymond Smullyan es un lógico autor de varios libros deliciosos como "¿Cómo se llama este libro?", "¿La dama o el tigre?" o, mi favorito, "5.000 años antes de Cristo y otras fantasías filosóficas". Éste es su silogismo favorito:
Algunos
coches traquetean,
Mi coche es algún coche,
Por lo tanto, no es de extrañar que mi coche traquetee.
Mi coche es algún coche,
Por lo tanto, no es de extrañar que mi coche traquetee.
Personalmente, la demostración más simpática que he encontrado en sus libros es esta prueba cartesiana de la existencia de Dios:
Dios tiene que existir, pues no iba a ser tan malo como para engañarme y hacerme creer que existe si en realidad no existiera.
POLINOMIOS CICLOTÓMICOS
Veamos una curiosidad numérica. Los polinomios ciclotómicos son los polinomios irreducibles con coeficientes racionales que tienen por raíces a las raíces de la unidad, es decir, a los números complejos que elevados a un número natural dan 1. Puesto que las raíces de la unidad son raíces del polinomio xn-1, los polinomios ciclotómicos se obtienen factorizando éstos. Por ejemplo, para n = 1, x-1 es ya el primer polinomio ciclotómico. Para n = 2, el polinomio x2-1 contiene al primer polinomio ciclotómico, y al quitárselo (dividiendo) queda x+1, que es el segundo polinomio ciclotómico. El polinomio x3-1 contiene al primer polinomio ciclotómico x-1, y al quitarlo queda x2+x+1, que es el tercer polinomio ciclotómico. A x4-1 hay que quitarle el primero x-1 y el segundo x+1. Al hacerlo obtenemos x2+1, que es el cuarto polinomio ciclotómico. En general se prueba que xn-1 es el producto de los polinomios ciclotómicos de orden d, donde d recorre los divisores de n, por lo que hay que dividirlo entre todos los polinomios correspondientes a divisores estrictos de n para obtener el polinomio n-simo. Es fácil ir calculándolos. Los primeros polinomios ciclotómicos, así obtenidos, son
- p1(x) = x-1
- p2(x) = x+1
- p3(x) = x2+x+1
- p4(x) = x2+1
- p5(x) = x4+x3+x2+x+1
- p6(x) = x2-x+1
p105(x) = x48
+ x47
+ x46 - x43 - x42 - 2x41
- x40 - x39 +x36 + x35+x34
+ x33 + x32 + x31
- x28 - x26 - x24 - x22 - x20 +x17 + x16+ x15 + x14 + x13 + x12 - x9 - x8 -2x7 - x6 - x5 + x2 + x + 1,
- x28 - x26 - x24 - x22 - x20 +x17 + x16+ x15 + x14 + x13 + x12 - x9 - x8 -2x7 - x6 - x5 + x2 + x + 1,
con dos flamantes doses (menos doses, en realidad). De hecho puede probarse que hay polinomios ciclotómicos con coeficientes arbitrariamente grandes en módulo. Tenemos así uno de los muchos ejemplos de lo arriesgado que es hacer una conjetura en teoría de números, aunque tengamos 104 evidencias empíricas.
 Un
ejemplo más famoso de conjetura falsa es la de Fermat, que
creyó
que un número de la forma 2n+1 es primo
si y sólo si n es potencia de 2. La necesidad de la
condición
es fácil de probar. La conjetura consiste en la suficiencia, que
se basa en los casos:
Un
ejemplo más famoso de conjetura falsa es la de Fermat, que
creyó
que un número de la forma 2n+1 es primo
si y sólo si n es potencia de 2. La necesidad de la
condición
es fácil de probar. La conjetura consiste en la suficiencia, que
se basa en los casos:21+1 = 3, 22+1
= 5, 24+1= 17, 28+1 =
257, 216+1 = 65.537.
También es un hecho conocido que fue Euler quien descubrió que
 UN PROBLEMA GEOMÉTRICO
UN PROBLEMA GEOMÉTRICO
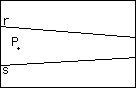
Tenemos dos rectas r y s que no
son paralelas, pero que se
cortan
fuera de la hoja de papel. También nos dan un punto P exterior a
ambas.
El
problema es trazar la recta que pasa por P y por el punto de corte, sin
más ayuda que una regla no graduada y, por supuesto, sin que la
construcción se salga del papel.
Aunque el problema en sí no deja de tener interés, es mucho más interesante su SOLUCIÓN.
Este problema puede resolverse por métodos completamente elementales:
También es un hecho conocido que fue Euler quien descubrió que
232+1
= 641.6.700.417.
Lo que no es tan sabido es cómo llegó a descubrir
esto. Pensemos que232+1
= 4.294.967.297,
y que Euler no tenía calculadora. Aunque la hubiera tenido,
no
es plan ponerse a dividir entre todos los primos hasta llegar al 641.
Si
tienes curiosidad por saber cómo puede encontrarse el factor
641, entra aquí. UN PROBLEMA GEOMÉTRICO
UN PROBLEMA GEOMÉTRICOAunque el problema en sí no deja de tener interés, es mucho más interesante su SOLUCIÓN.
Encontrar
todos los números naturales (no nulos) que pueden expresarse
simultáneamente como producto de dos y tres números
consecutivos.
Hay una solución trivial: 6
= 2.3 = 1.2.3, y puede demostrarse que
sólo
hay una solución más, aparte de ésta. Demostrar
que
no hay otras es un problema muy difícil, resuelto por Mordell en
1962. Sin embargo, encontrar dicha solución está al
alcance
de cualquiera (no es muy grande). ¿Cuál es?UN
PROBLEMA ALGEBRAICO (MÁS FÁCIL)
Este problema puede resolverse por métodos completamente elementales:
Demostrar
que las únicas potencias de 2 que son consecutivas con potencias
de 3 son 2,3,4 y 8, 9.
| Soneto
a la convergencia de 1/n |
| La sucesión que viene
definida por an igual, exactamente, al inverso de n, es convergente, lo cual demostraremos enseguida: |
| Para toda distancia preelegida al conjunto R+ perteneciente (ε, por ejemplo), es evidente, por una propiedad muy conocida, |
| que el inverso de ε se puede superar por un m natural y, para todo n mayor, sucede |
| que excede a dicho inverso por
igual, y esto hace, pues, que an quede cercano a 0 bajo el radio tal. |
| Carlos Ivorra |