ejercicios CHI-2 , F ,T , NORMAL-M
1. Un determinado estadístico J se distribuye según
un modelo jhi-dos de parámetro (grados de libertad) 14 . Deseamos saber la probabilidad
con la que dicho estadístico tomará un valor menor que 9,467. (Ir a
solución)
2. Otro estadístico se
distribuye según una c 2 con 20 grados de libertad ¿Cuál será el valor de dicho
estadístico para el que se genera un nivel de significación del 0,05 % ? (Ir a solución)
3.
Dada una variable aleatoria que se distribuye como una t de Student con 16 grados de
libertad .
a)Calcular la probabilidad de que dicha
variable tome valores menores que 1.071 .
b)Calcular la probabilidad de que dicha
variable( en valor absoluto) tome valores menores que 1.071.
c)Conociendo que la probabilidad de que la
variable en valor absoluto sea superior a un valor (crítico) es 0,1 Calcular
dicho valor crítico . (Ir
a solución)
4.
Una variable se distribuye como una F de Snedecor de parámetros 3 y 7 .
Calcular la probabilidad de que dicha variable tome valores superiores a 8,45 . (Ir a solución)
5.
El ratio comercial A se distribuye según una N[12,4] um. Y el ratio B como otra normal de
media 10 y varianza 25 , Entre ambos ratios existe una correlación de 0,8 . Según
estudios realizados el mejor indicador económico que debemos utilizar es uno tal cuya
estructura es R=5A+2B+1.
a)Calcular la probabilidad de que
dicho ratio R tome el valor 83 .
b)Calcular
la probabilidad de que R tome valores superiores a 84 . (Ir a
solución)
6.
Una pieza tiene de longitud L que es normal de media 10 cm. y varianza 0,1 cm. al cuadrado
. Se le lija 1 cm. que evidentemente no es preciso y perfecto lo es más o menos según
una normal de media 1 cm y desviación 0,1 cm . Una pieza es buena si su longitud está
comprendida entre 8,8 y 9,2 cm .Si preparamos 10 piezas ¿Cuál es la probabilidad de que
al menos 9 de ellas sean buenas ? (Ir a solución)
7.El
número de personas que compran en una tienda es aleatorio , pero por término medio se
supone que este número es de 5 en una hora. Calcular la probabilidad de que en dos horas
hayamos hecho exactamente 8 ventas.
(Ir a solución)
8.
Dos cadenas de montaje convergen a un único taller de acabado que durante cinco minutos
trata a una sola unidad. El tiempo que las unidades están en cada cadena es aleatorio y
con distribución normal. Independiente de una cadena a otra , con parámetros :
cadena A ® N[12 ;4] .
cadena B ® N[9 ;3] ambas en minutos
Si a las doce horas entra a la cadena A una unidad y ocho minutos después entra a la
cadena B otra unidad.
a)¿ Cuál es la probabilidad de que la unidad de B llegue al taller de acabado antes que
la unidad A ? 0,1587
b)¿Cuál es la probabilidad de que cuando llegue la unidad de B puede ser ésta tratada
sin demora ? (Ir a solución)
9. Dada una variable
aleatoria bidimensional (x ;y) con distribución normal bivariante de parámetros
m
=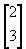 v =
v =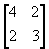 determinar
determinar
a)
P(1,5< x< 2,5) .
b) siendo z=2x+y calcular P(Z<
2)
c) siendo z=2x-y calcular
P(z<2)
(Ir a solución)
ir a imprimible de todos resueltos
ir a chi-2 , t , f, normal-m
![]() v =
v =![]() determinar
determinar