Desarrollo

    En el applet de abajo, se representa el montaje de la experiencia en el Laboratorio. Los polímetros miden la diferencia de potencial e intensidad en el circuito (superior) de la bombilla y la diferencia de potencial en los extremos del fotodiodo, en el circuito inferior. Como la respuesta lineal del fotodiodo sólo se produce a intensidades bajas, evitamos una irradiación alta situando la pantalla, que sólo permite regular el paso de de la radiancia de la bombilla (entre un 0% y un 100%). Junto al fotodiodo se ha instalado un filtro de longitud de onda λ= 578nm.

    El circuito es operado de forma sencilla: con el autotransformador regulamos la diferencia de potencial que podemos medir con el voltímetro que hay en bornes de la bombilla de tungsteno. El amperímetro, situado en serie con la bombilla nos da la lectura de la intensidad que atraviesa el filamento incandescente.

    Las medidas que vamos a realizar serán de voltaje e intensidad de corriente (lecturas de los multímetros), únicas medidas a las que tenemos acceso directo; el resto de magnitudes deberán ser puestas en función de éstas. En lo que sigue, denominaremos V a la diferencia de potencial aplicada en bornes de la bombilla e I a la intensidad que circula a través del filamento. A la diferencia de potencial de salida del fotodiodo lo denominaremos V_d.

    Con los datos de las ternas V, I, V_d (es conveniente tomar alrededor de 40 medidas), manipulados adecuadamente, llegaremos a cumplir los objetivos propuestos para el experimento.

1)

Puesta a prueba de la ley de Stefan-Boltzmann: determinación del rango de voltajes V adecuados.

    En primer lugar, someteremos a prueba la ley de Stefan-Boltmann. Para ello, utilizaremos la relación (7); si en ella sustituimos la temperatura por la relación (10), y tomamos logaritmos, llegamos a:

    Así, si nuestra hipótesis de que el filamento se comporta como cuerpo negro es correcta, entonces debe seguir la ley de Stefan-Boltzmann, y al representar ln (P) (recordamos, P es la potencia que emite la bombilla, que, en términos de variables eléctricas, es P=V·I) en función de ln (R), deberíamos obtener una línea recta.

    A continuación, mediante la lectura de los tres polímetros, rellene la Tabla1 introduciendo los valores en la Tabla 0 y pulsando en el botón insertar.
Tome entre 10 y 15 medidas para voltajes entre 1V y 50 V del autotransformador y entre 20 y 25 medidas para voltajes entre 50V y 230V. Para mover los diales, ha de presionar las flechas del teclado a izquierda y derecha o arriba y abajo, pinchando previamente con el ratón en cada dial.

Nota:
La medida de la radiancia con un fotodiodo se basa en el hecho de que, fijada la frecuencia, la medida de la intensidad medida (o voltaje) es proporcional a la radiancia que le llega al fotodiodo. Ésto puede no ser así si la intensidad de la radiación es muy elevada, produciéndose un efecto típico de saturación del componente. Hemos comprobado que una región segura de trabajo, para todas las potencias de la bombilla, se obtiene con aperturas no mayores del 50%. Por ello, si va a utilizar aperturas superiores al 50% verifique, mediante la gráfica 0, qué rango de valores del la potencia de la bombilla no producen saturación de la corriente del fotodiodo, eliminado aquellos valores del voltaje de la bombilla en los que la gráfica 0 no es lineal.

Necesita instalar para ver el applet. Obtener

Tabla 0              Apertura:   %
V (V)	I (mA)	Vd (mV)	Insertar Valores

Ocultar Gráf.0      Mostrar Gráf.0

Necesita instalar para ver el applet. Obtener

2)

    En la columna 1, marque todos los puntos introducidos, apriete calcular y dibuje la gráfica ln (P) frente a ln (R),. ¿Los puntos experimentales están alineados?. ¿Entiende por qué?

(Vea esta ayuda si necesita una explicación o quiere comprobar la suya).

    Observando el resultado, intentedeterminar a partir de qué voltaje los puntos de la gráfica anterior están alineados (para una apertura de ranura del 50% esto debe ocurrir par voltajes superiores o iguales a 50V).

Necesita instalar para ver el applet. Obtener

3)

Puesta a prueba de la ley de Stefan-Boltzmann: determinación de

    En la columna 1 de la Tabla 1 desmarque ahora todos aquellos puntos que no aparecen alineados en la gráfica anterior. Pulse Trasladar y observará que los puntos escogidos han pasado a la Tabla 2. Pulse ahora dibujar y verifique que los puntos experimentales están alineados con la recta obtenida mediante un ajuste por mínimos cuadrados.

Necesita instalar para ver el applet. Obtener

4)

    A partir de la pendiente de la gráfica anterior y su error determine el valor de e introdúzcalo en la Tabla 3. Compruebe que su cálculo es correcto.

5)

Comprobación de la distribución de Planck: obtención de la constante de Planck, h.

    Para comprobar que el fenómeno de radiación del cuerpo negro aplicado a nuestro filamento de tungsteno incandescente viene regido por la distribución de Planck, utilizaremos su representación en función de la longitud de onda, λ, en la aproximación dada por (6). Si en ella sustituimos R_λ(T) por V_d según la relación (8), y tomamos logaritmos, obtenemos:

    Si ahora en (12) sustituimos la temperatura por su expresión en función de la resistencia (10), llegamos, finalmente, a:

    Si la hipótesis formulada es correcta, una representación ln Vd frente a (recordamos que la resistencia será R = V/I) debe dar lugar a una línea recta. En la Tabla 4, pulse el botón calcular para obtener los valores de correspondientes a los valores medidos. Pulse ahora dibujar y verifique que los puntos están alineados con la recta obtenida mediante un ajuste por mínimos cuadrados. De la pendiente de la recta, conocido un par de referencia R₀, T₀ (R₀=25Ω para T₀=295K, con la bombilla utilizada) y las constantes k y c (el valor de lo tenemos del apartado anterior del experimento), podemos obtener un valor de la constante de Planck, con su error.

Necesita instalar para ver el applet. Obtener

    Introduzca el valor obtenido (h), con su error, en la Tabla 5 y compruebe su resultado. Compare con el que figura en los libros de texto.

Ayuda: para el cálculo del error de h considere el error de la pendiente dado en la gráfica anterior, el error de 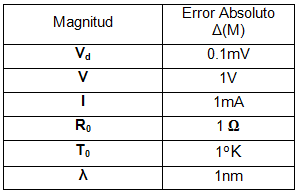calculado en el apartado 4) y como error en las medidas de las magnitudes, el dado en la siguiente tabla:

Considere suma de errores cuadráticos

    Si la comprobación del resultado le indica que éste no es correcto puede consultar aquí la fórmula que da el error de h en términos de los errores de las demás magnitudes, realizando la adecuada propagación de errores.