| Se define como el
error en régimen permanente como la diferencia o discrepancia entre el valor de
referencia y el valor de la salida una vez alcanzado el equilibrio. |
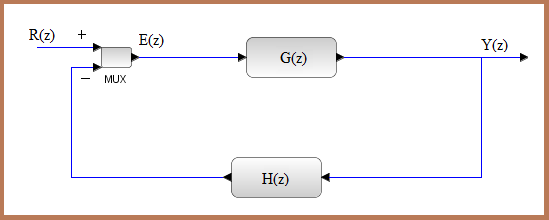 |
| Lo que queremos al
regular el sistema es conseguir que el error E(z) valga cero. En este momento
la acción de control habrá llegado a su fin. |
| E(z) = R(z) – H(z)*Y(z) |
| E(z) = R(z) – H(z)*G(z)*E(z) |
|
E(z)*[1 + H(z)*G(z)] = R(z) |
|
|
| El error en régimen
permanente es deducir cuanto vale está expresión en el infinito. Esto lo
hacemos mediante el teorema del valor final: |
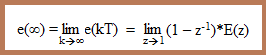 |
| El error como vemos
depende de la referencia R(z) y del tipo de sistema. El tipo de sistema se
define como la cantidad de polos en z=1 en bucle abierto que tiene un sistema. Hay
tres tipos de errores dependiendo de cómo son nuestras referencias: el error de
posición, de velocidad y de aceleración. |
| -Error de posición: Se da cuando la entrada es un escalón: |
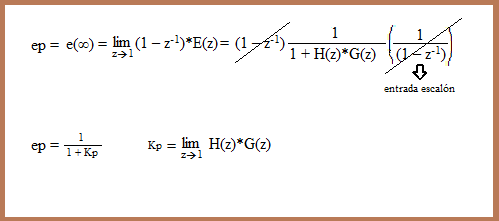 |
| Cuando el sistema es
de tipo 1 o superior el coeficiente estatico Kp del error de posición varia, y
el error de posición se hace cero. |
| -Error de velocidad: Se da cuando la entrada es una rampa: |
 |
|
-Error de aceleración: Se da cuando la entrada es una parábola: |
 |
| Pero todo lo explicado hasta el momento, lo podemos resumir en la siguiente tabla: |
| Error\\Tipo |
0 |
1 |
2 |
| Ep |
1/(1+Kp) |
0 |
0 |
| Ev |
∞ | 1/Kv |
0 |
| Ea | ∞ | ∞ | 2/Ka |
| Ejemplo: |
| Calcular el error en régimen permanente de: |
 |
|
Empezamos por el error de posición: |
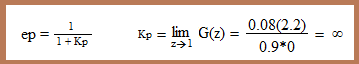 |
| Seguimos con el error de velocidad: |
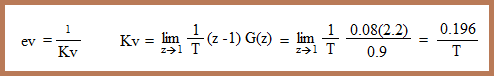 |
| Y terminamos con el error de aceleración: |
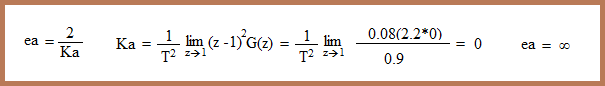 |
| Como vemos, la tabla que hemos mencionado se cumple a la perfección. |
 |
 |
 |
 |
||
 |
||