Función de Transferencia

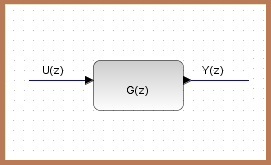
Supongamos que tenemos un modelo de un sistema discreto con una sola entrada U y una sola salida Y, como la que se ve en la imagen:

Supongamos que el sistema viene dado por una ecuación en diferencias tal como esta:

y(k) + a1*y(k-1) + a2*y(k-2) +…+ an*y(k-n) = b0*u(k) + … + bn*y(k-n)

Aplicando la transformada Z junto a la propiedad del desplazamiento temporal tendríamos lo siguiente:

y(z) + a1*z^-1*y(z) + a2*z^-2* y(z) + … + an*z^-n* y(z) = b0*u(z) + …+ bn*z^-n*u(z)

Despejando el cociente y(z)/u(z) tenemos:

y(z)*[1 + a1*z^-1 + a2*z^-2 + … + an*z^-n] = u(z)*[b0 + …+ bn*z^-n]

y(z)/u(z) = (1 + a1*z^-1 + a2*z^-2 + … + an*z^-n)/ (b0 + …+ bn*z^-n)

A dicho cociente se le denomina función de transferencia directa del sistema y se suele denotar como G(z)

Tiene muchísimas utilidades, pero lo más importante es que contiene toda la información que necesitamos para analizar un sistema discreto. Gracias a ella podemos trabajar muy cómodamente con los bucles de control, podemos analizar los polos y los ceros y transformar y antitransformar en Z.

Ahora bien, ¿Cómo obtenemos en la práctica una función de transferencia?

Para hallarla debemos seguir los siguientes cuatro pasos:

1) Planificación experimental: Se selecciona la entrada y se registra la salida. En algunos casos no es tan sencillo, puesto que la entrada viene impuesta y no podemos poner una entrada sencilla, como un impulso.

2) Selección de la estructura del modelo: Atendiendo a la salida del sistema observada se selecciona el orden del sistema, el retardo…etc.
(Este punto se analiza con más profundidad a continuación)

3) Estimación de los parámetros: Supuesto el modelo se obtienen de diferentes formas los parámetros incógnitas.

4) Validación: Una vez obtenido el modelo es necesario comprobar si responde ante la misma excitación de entrada. Si la validación resulta insatisfactoria hay que volver al paso 2.

El punto uno, tres y cuatro más o menos están claros, pero el segundo punto quizás no tanto. Por ello vamos a analizar un método por el cual se obtiene una estructura del modelo.

Normalmente se plantea un modelo. Es el planteamiento más sencillo, pero menos exacto. Supongamos que tenemos una entrada escalón o impulso. A partir de esto suponemos un determinado modelo y procedemos al paso tres: estimación de los parámetros incógnita.

Con un ejemplo lo veremos más sencillo:

Imaginemos tener un motor de corriente continua que arrastra una plataforma y experimentalmente siguiendo el paso uno se han obtenido los siguientes datos

N	SALIDA
0	0
1	0
2	0
3	1
4	1.2
5	1.65
6	1.94
...	...
36	3.19

(PASO 2)

En primer lugar, por las tres primeras entradas podemos deducir que tiene un retardo de tres, puesto que sus tres primeras entradas son cero. En cuanto al orden lo suponemos de momento uno. Con esto obtenemos un G(z) como este:

Es decir la secuencia se queda: y_k = bu_k-3 + ay_k-1

(PASO 3)

Ahora dándole los valores de la tabla obtenemos los valores de las incógnitas:

y0 = b(u-3) + a(y-1) = 0 (no extraemos nada de aquí)

y1 = b(u-2) + a(y0) = 0 (no extraemos nada de aquí)

y2 = b(u-1) + a(y1) = 0 (no extraemos nada de aquí)

y3 = b(u0) + a(y2) = 1; b=1

y4 = b(u1) +a(y3) à b +ab = 1.2 à 1 +a =1.2 ; a = 0.2

El resultado es el siguiente:

(PASO 4)

Ahora validamos el resultado, mediante el teorema del valor final:

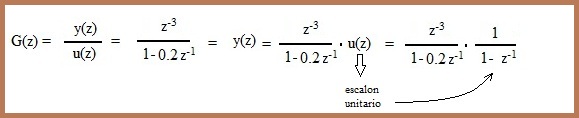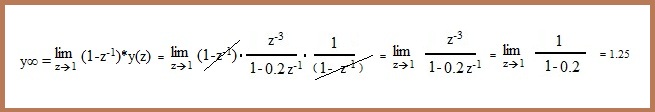Conclusión: y∞ = 1.25 no se parece al máximo valor que nos da la tabla que es y36 =3.19. Es decir, que hay que probar otro modelo. Si probamos el modelo de orden dos simplemente debemos multiplicar nuestro modelo por dos(G(z)^2):

Repitiendo procedimiento como antes, nos saldrán mas ecuaciones y mas incógnitas, y si no nos da tendremos que aumentar el orden hasta que al final la y∞ de similar a 3.19.

Hay otros métodos para obtener un modelo como por ejemplo el de los mínimos cuadrados, pero son más costosos puesto que necesitan entradas persistentes y no entradas sencillas como un impulso. Por ello no los analizaremos aquí.

En conclusión vemos que es esencial extraer la función de transferencia de un sistema discreto antes de analizarlo, ya que toda la información importante para analizar un sistema se encuentra en esta. Y además hemos visto como extraerla: planificación experimental, selección de la estructura de un modelo, estimación de los parámetros, y validación.