| Podemos definir un sistema como estable
cuando su salida está acotada. Es decir, que su salida no es ±∞ sino un valor
concreto. También podríamos definir a un sistema estable que evoluciona de un
modo similar a la variable de entrada. |
| En un sistema en bucle abierto solo
estudiaríamos nuestro proceso con el regulador, o incluso sin él: |
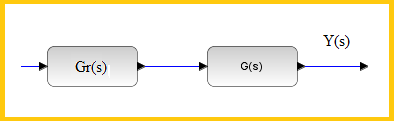 |
| Pero en el bucle cerrado, estudiaríamos
nuestro sistema, más la realimentación. Lo cual complica un poco las cosas: |
|
| Cada uno se estudia de una forma. En el caso
del bucle abierto, la estabilidad se puede analizar mediante los polos y ceros
del sistema. Como mencionamos en el tema de la “función de transferencia
directa” obteníamos un cociente de dos polinomios. El valor de Z para el cual
el numerador de la función de transferencia directa vale cero, son los ceros.
Por contra, el valor de Z para el cual el denominador de la función de transferencia directa es cero,
son los polos. |
|
Ejemplo: |
| Para la función de
transferencia: |
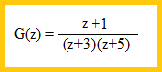 |
| Hay solo un cero,
que seria el valor para el cual el numerador se haría cero: z = -1 |
| En el caso de los
polos, hay dos. Los valores que harían cero el denominador son: z = -3 y z = -5 |
|
En Scilab se calcularía del siguiente modo: |
|
|
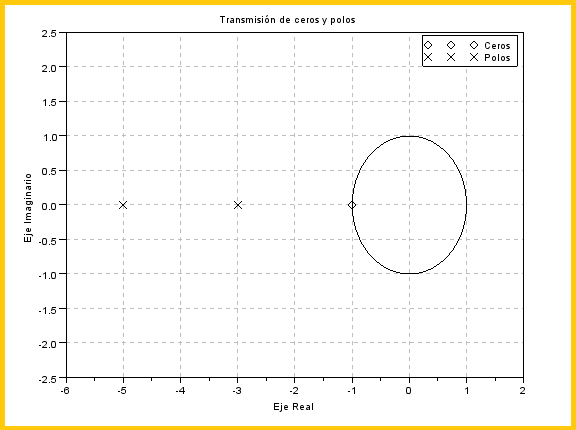
| Se usaría el
comando roots para extraer los polos y los ceros de la función de
transferencia; y luego se graficarían los polos y los ceros de la función de
transferencia directa mediante el comando plzr() quedando dicho grafico así: |
 |
|
La
importancia de los polos y los ceros erradica en que en un sistema de bucle
abierto, el sistema será estable si sus polos se encuentran dentro del circulo
unidad |
| En el
caso de que el sistema con bucle cerrado es más complicado, puesto que para
saber que sea estable, las raíces de su ecuación característica deben estar en
la región estable (ya sea del plano S o Z). La ecuación característica la
podemos ver mejor con esta imagen. |
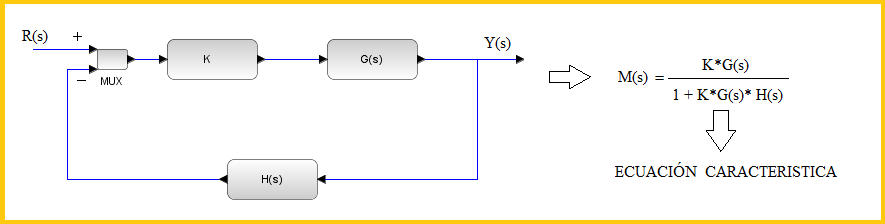 |
| Los valores que hagan cumplirse esta
expresión: |
| 1 + K*G(s)*H(s) = 0 |
| Si están en la región estable, el sistema
entero será estable, pero como vemos la ecuación característica depende de K.
Hay diversos métodos para estudiar la estabilidad de un sistema. Por ejemplo
está el criterio de Routh-Hurwitz, que mediante una tabla nos da un
rango de valores de K para el cual el sistema es estable. Pero con programas
como Scilab no nos hace falta puesto que analizando el lugar de las raices
podemos saber donde el sistema se hace o no inestable. |
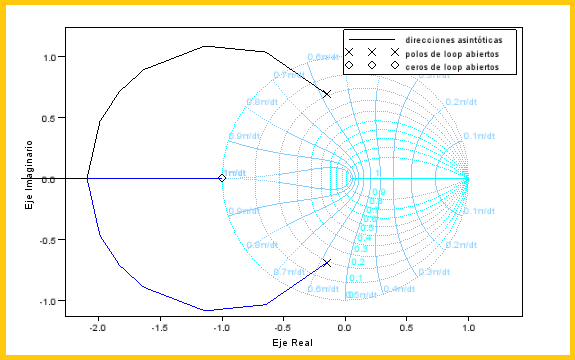
| Ejemplo de un lugar
de las raíces para un sistema en bucle cerrado: |
 |
| En Scilab lo podriamos hacer del siguiente
modo: |
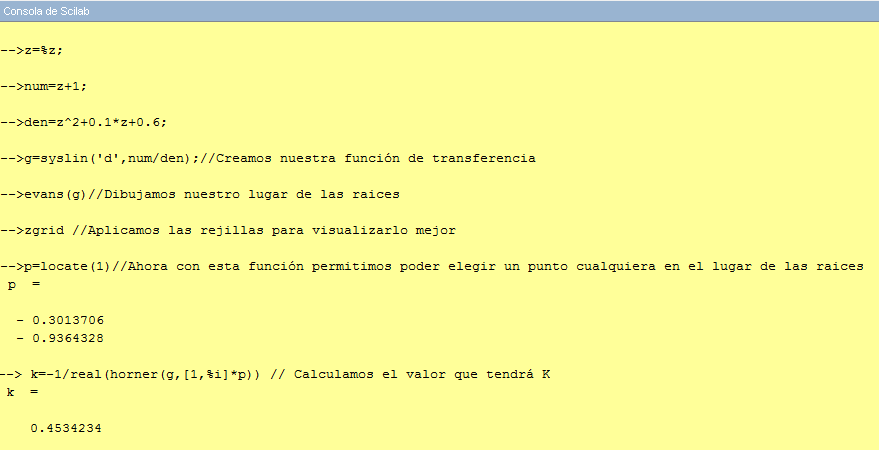 |
| Con esto podemos
obtener la K. En este caso en el ejemplo he obtenido el siguiente punto: |
|
| Gracias a que podemos
ver el punto que deseamos elegir, podemos elegir nuestro punto en un lugar
dentro del círculo unidad. Por lo que está K elegida hará al sistema estable. Y
de ese modo controlamos la estabilidad en bucle cerrado de nuestro sistema. |
|
En conclusión, para
estudiar la estabilidad habrá que distinguir si el sistema está en bucle
abierto o cerrado. Si el sistema está en bucle abierto solo tendremos que
estudiar los polos para ver si están dentro del circulo unidad o en el
semiplano negativo. Sin embargo en bucle cerrado, tendremos que analizarlo con
el lugar de las raíces y elegir un punto siguiendo una especificaciones y que
este dentro del circulo unidad o el semiplano negativo, para obtener una K que
nos hará estables el sistema. |