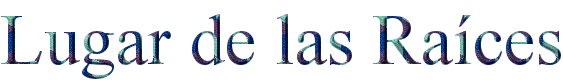Lugar de las raíces

Como vemos visto en el subtema de: "Función de transferencia directa", la función de transferencia de un sistema nos aporta mucha información del sistema. Una herramienta muy útil con la que podemos trabajar es el lugar de las raíces. Su importancia erradica en que nos permite saber la posición de los polos y los ceros en un sistema de lazo cerrado cuando variamos un parámetro ajustable. El lugar de las raíces se puede hacer de un sistema continuo o de un sistema discreto. No nos pararemos a explicar como se dibuja un lugar de las raíces ya que es un proceso extenso y que hoy en día con el programa Scilab es muy sencillo con el comando "evans()".En nuestro caso convertimos señales continuas a señales discretas, con lo que es importante saber las equivalencias entre uno y otro.

En el caso del plano S este trabaja por coordenadas rectangulares. Un "s= σ +jω" en el plano S (usando Scilab y la función 'evans') se representaría de la siguiente forma:

Representacion en S

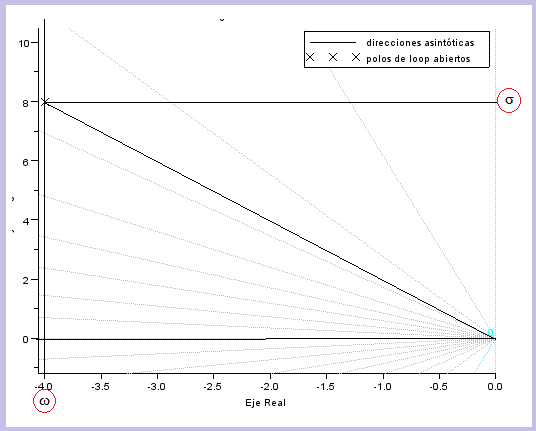
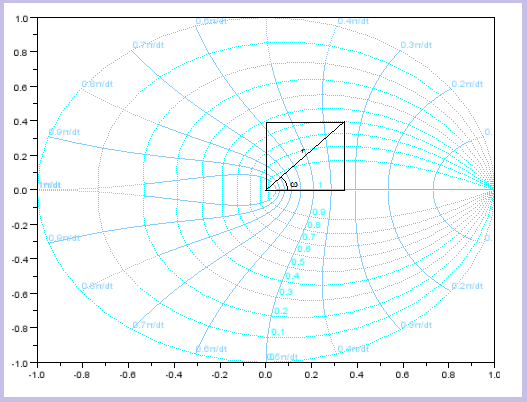
Sin embargo en el plano Z usa coordenadas polares. Este mismo punto (usando de nuevo el entorno Scilab y la función Evans) se reflejaría de otra forma:

Plano Z Equivalencia

La relación de ambos planos se encuentra en la expresión:

z = e^sT

o lo que es lo mismo:

z = e^-^σ^T*[cos(ω*T) ± sen(ωT)j]

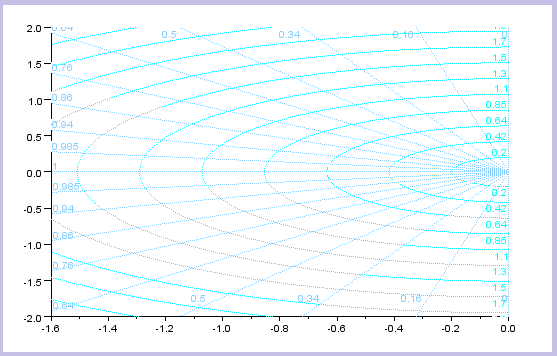
Así, vemos que las regiones de estabilidad en cada uno de los planos son las siguientes:

Región estable en el plano S	Región estable en el plano Z

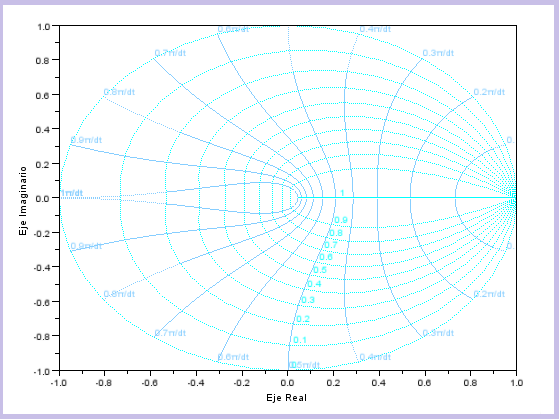En el caso del plano S la región de estabilidad está a la izquierda del eje imaginario. En el caso del plano Z la región de estabilidad está dentro del círculo unidad. Esto se debe a que el semiplano negativo del plano S se "transforma" en el interior del circulo unidad.

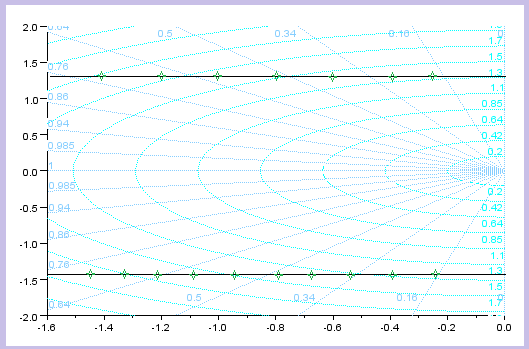
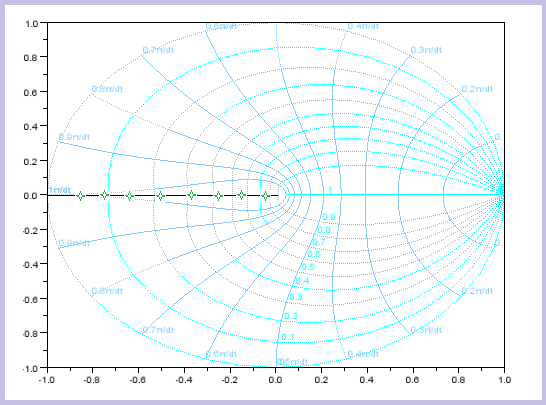
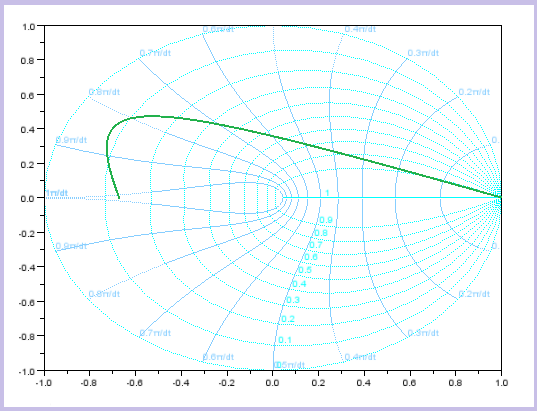
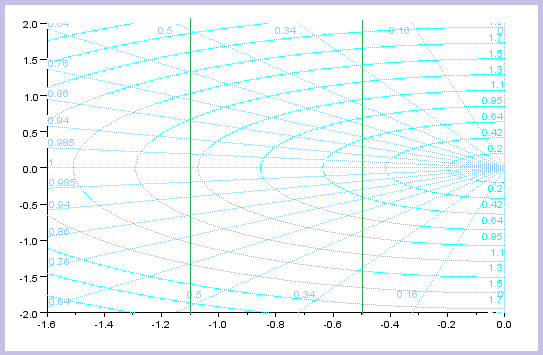
Veamos algunas equivalencias entre el plano S y el plano Z:

PLANO S	PLANO Z

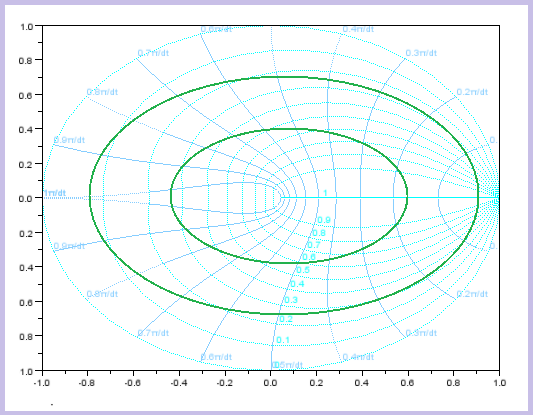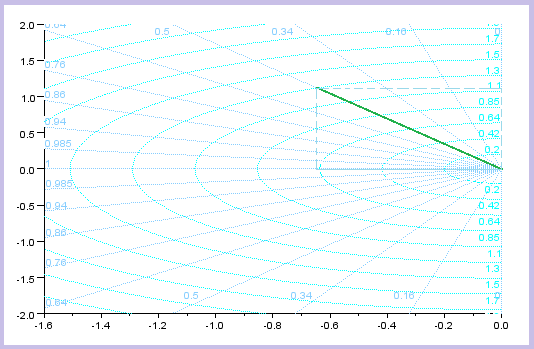
Las estrellas verdes o las líneas verdes marcan los puntos que estarían en el plano S y como se transformarían al plano Z

Si recordamos el tema de muestreo, la importancia de la frecuencia de muestreo era vital. En esta parte es donde aparecen las formulas del teorema de muestreo de Nyquist-Shannon:

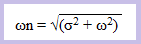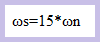Veamos un ejemplo en el que podamos ver la importancia de discretizar bien:

Ejemplo de la influencia del periodo de muestreo:

Discretizar: s = -2±3j

σ = -2; y ω = 3;

Cumpliendo con la formula numero uno de arriba tenemos que la raíz de la suma de los cuadrados da 3.605 y de este modo obtenemos "ωn"

Esto multiplicado por 15 (siguiendo la formula tercera) nos da un resultado 54.083rad/s que seria la "ωs"

Y por ultimo y siguiendo la formula dos, y dividiendo 2π entre la "ωs" obtenemos el periodo de muestreo: 0.116 segundos

La importancia del periodo de muestreo la vemos a continuación:

Si discretizamos por la formula mencionada al principio (z=e^sT= e^-^σ^T*[cos(ω*T) ± sen(ωT)j] ) y lo hacemos con el periodo de muestreo que hemos obtenido( 0.1 segundos) obtenemos el siguiente un resultado:

e^-^2*0.1*[cos(3*0.1) ± sen(3*0.1)j] = 0.782 ± 0.242j

Pero sin embargo sin usamos otra frecuencia de muestreo, pongamos 0.5, la diferencia se aprecia bastante:

e^-^2*0.5*[cos(3*0.5) ± sen(3*0.5)j] = 0.026 ± 0.367j

Por lo que aquí vemos la importancia del primer tema y la importancia de un buen periodo de muestreo.

Como hemos mencionado anteriormente a nosotros nos interesa más el comportamiento del lugar de las raíces en el plano Z. Esta imagen ilustra bastante bien el comportamiento de los diferentes sistemas dependiendo de donde se encuentren los polos de nuestra función de transferencia:

Vista la equivalencia del plano S y el plano Z y analizada la importancia del periodo de muestreo, en el siguiente tema se analiza la estabilidad.

Región estable en el plano S

Región estable en el plano Z

PLANO S

PLANO Z

Ejemplo de la influencia del periodo de muestreo: