Gráficos
Vicente Coll & Pedro J. Pérez
Junio 2017
1. Introducción.
En R tenemos disponibles distintos sistemas gráficos, aunque los más comunes son:
- Sistema gráfico base de R (autor:
R Core Team and contributors). El núcleo (core en inglés) gráfico en R se encuentra en los paquetes graphics (contiene las funciones de gráficos base: plot, hist, etc.) y grDevices (que implementa los distintos dispositivos gráficos: pdf, ps, png, …). - Lattice (autor:
Deepayan Sarkar). El libro Lattice. Multivariate Data Visualization with R (http://www.springer.com/gp/book/9780387759685) proporciona una gran cantidad de ejemplos (con código R).

Lattice (Deepayan Sarkar, 2008)
- ggplot2 (autor:
Hadley Wickham). Hadley Wickham ha escrito un libro en el que explica de forma muy didáctica los fundamentos para elaborar gráficos con este paquete. En este enlace lo encontraréis http://link.springer.com/book/10.1007%2F978-3-319-24277-4 (desde un ordenador de la Universitat de València se puede descargar, ¡tenemos acceso!).

ggplot2 (Hadley Wickham, 2016)
En este tutorial vamos a aprender a crear gráficos (básicos), puesto que constituyen herramientas enormemente valiosas para transmitir información. “Más vale una imagen que mil palabras”.
Comenzaremos haciendo distintos tipos de gráficos usando el sistema base y después los replicaremos utilizando ggplot2.
2. Gráficos base.
Para realizar los gráficos de este tutorial vamos a utilizar datos que se encuentran accesibles en el paquete AER. Por tanto, cargamos la librería AER (si no la tenemos hay que instalar el paquete).
if(!require("AER")) {install.packages("AER")}El paquete AER contiene más de 100 bases de datos (data sets). ¿Recordamos cómo podemos obtener el listado de datos que contiene un paquete?
data(package="AER")La base de datos que utilizaremos para crear las gráficas de este tutorial es CPS1985 (más información aquí). Primero cargamos la librería y luego cargamos la base de datos.
library(AER)
data("CPS1985")¿Cuántas observaciones hay? ¿Qué variables contiene la base de datos CPS1985?
dim(CPS1985)## [1] 534 11names(CPS1985)## [1] "wage" "education" "experience" "age" "ethnicity"
## [6] "region" "gender" "occupation" "sector" "union"
## [11] "married"Así pues, tenemos un total de 554 observaciones y las siguientes 11 variables:
- Wage: Wage (dollars per hour).
- Education: Number of years of education.
- Experience: Number of years of work experience.
- Age: Age (years).
- Ethnicity: Race (1=Other, 2=Hispanic, 3=White).
- Region: Indicator variable for Southern Region (1=Person lives in South, 0=Person lives elsewhere).
- Gender: Indicator variable for sex (1=Female, 0=Male).
- Occupation: Occupational category (1=Management, 2=Sales, 3=Clerical,4 =Service, 5=Professional, 6=Other).
- Sector: Sector (0=Other, 1=Manufacturing, 2=Construction).
- Union: Indicator variable for union membership (1=Union member, 0=Not union member).
- Married: Marital Status (0=Unmarried, 1=Married)
Antes de comenzar con los gráficos, vamos a obtener un resumen de las variables.
summary(CPS1985)## wage education experience age
## Min. : 1.000 Min. : 2.00 Min. : 0.00 Min. :18.00
## 1st Qu.: 5.250 1st Qu.:12.00 1st Qu.: 8.00 1st Qu.:28.00
## Median : 7.780 Median :12.00 Median :15.00 Median :35.00
## Mean : 9.024 Mean :13.02 Mean :17.82 Mean :36.83
## 3rd Qu.:11.250 3rd Qu.:15.00 3rd Qu.:26.00 3rd Qu.:44.00
## Max. :44.500 Max. :18.00 Max. :55.00 Max. :64.00
## ethnicity region gender occupation
## cauc :440 south:156 male :289 worker :156
## hispanic: 27 other:378 female:245 technical :105
## other : 67 services : 83
## office : 97
## sales : 38
## management: 55
## sector union married
## manufacturing: 99 no :438 no :184
## construction : 24 yes: 96 yes:350
## other :411
##
##
## En el caso de variables cuantitativas, la función summary() proporciona como resumen de la variable los “cinco números” (mínimo, cuartil 1, cuartil 2, cuartil 3, máximo) y la media. Si el variable es categórica proporciona el total de observaciones en cada categoría.
Bien. Ya tenemos una idea de los datos. Ahora…a representarlos!!!!
Histograma.
Vamos a comenzar por representar un (sencillo) histograma del Salario (wage). La función que utilizamos es hist().
hist(CPS1985$wage)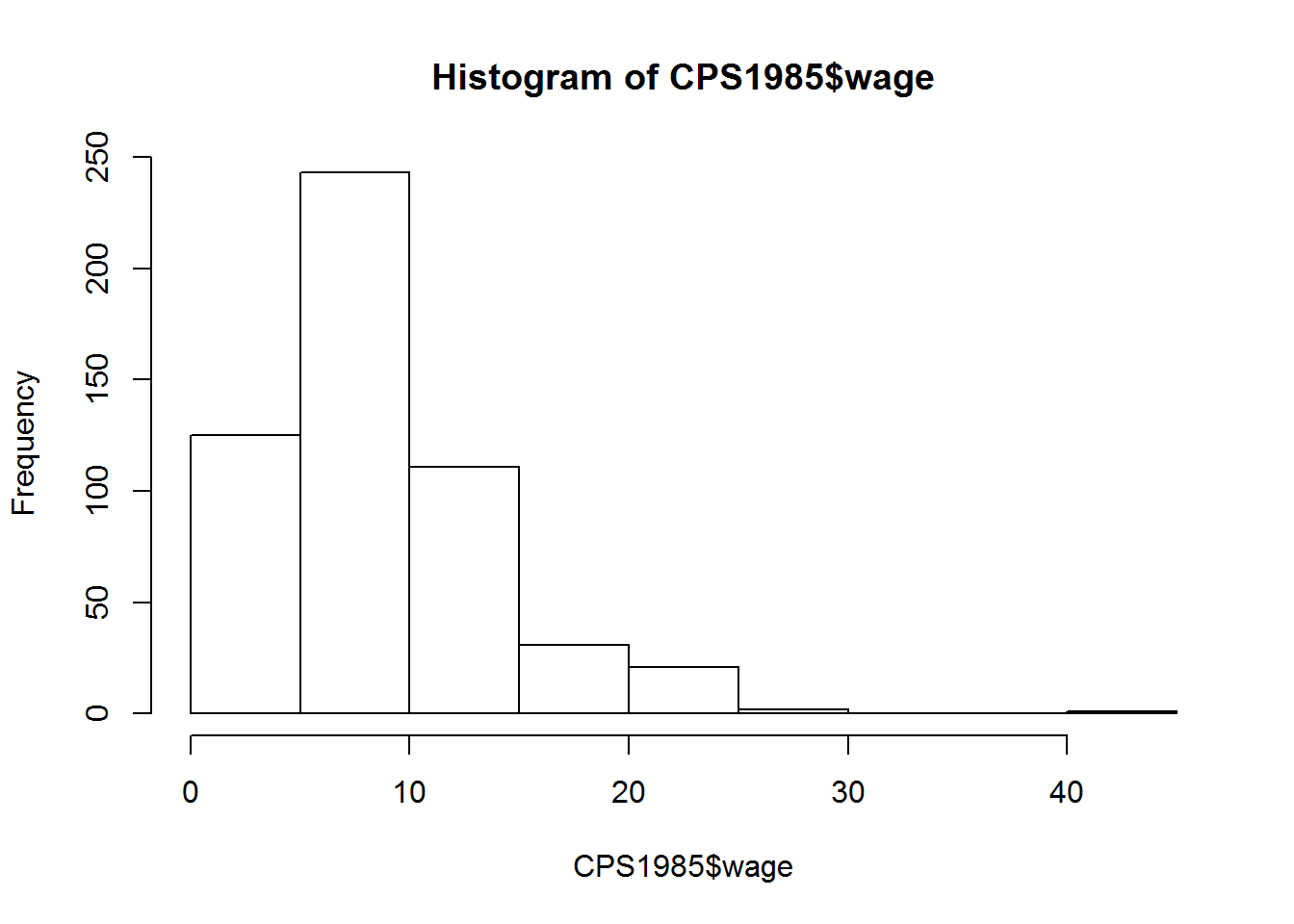
Así queda un poco feo. ¿Qué podemos hacer para mejorarlo?
Antes que nada, como no vamos a abrir ninguna otra base de datos, para evitar tener que escribir continuamente CPS1985$variable, hacemos un attach. Esto nos permite acceder directamente a las variables de CPS1985 (y nos evitamos escribir mucho).
attach(CPS1985) # acceder directamente a las variables (columnas)
p<-hist(wage)
text(p$mids,p$counts,labels=p$counts, adj=c(0.5, -0.5), cex=.5)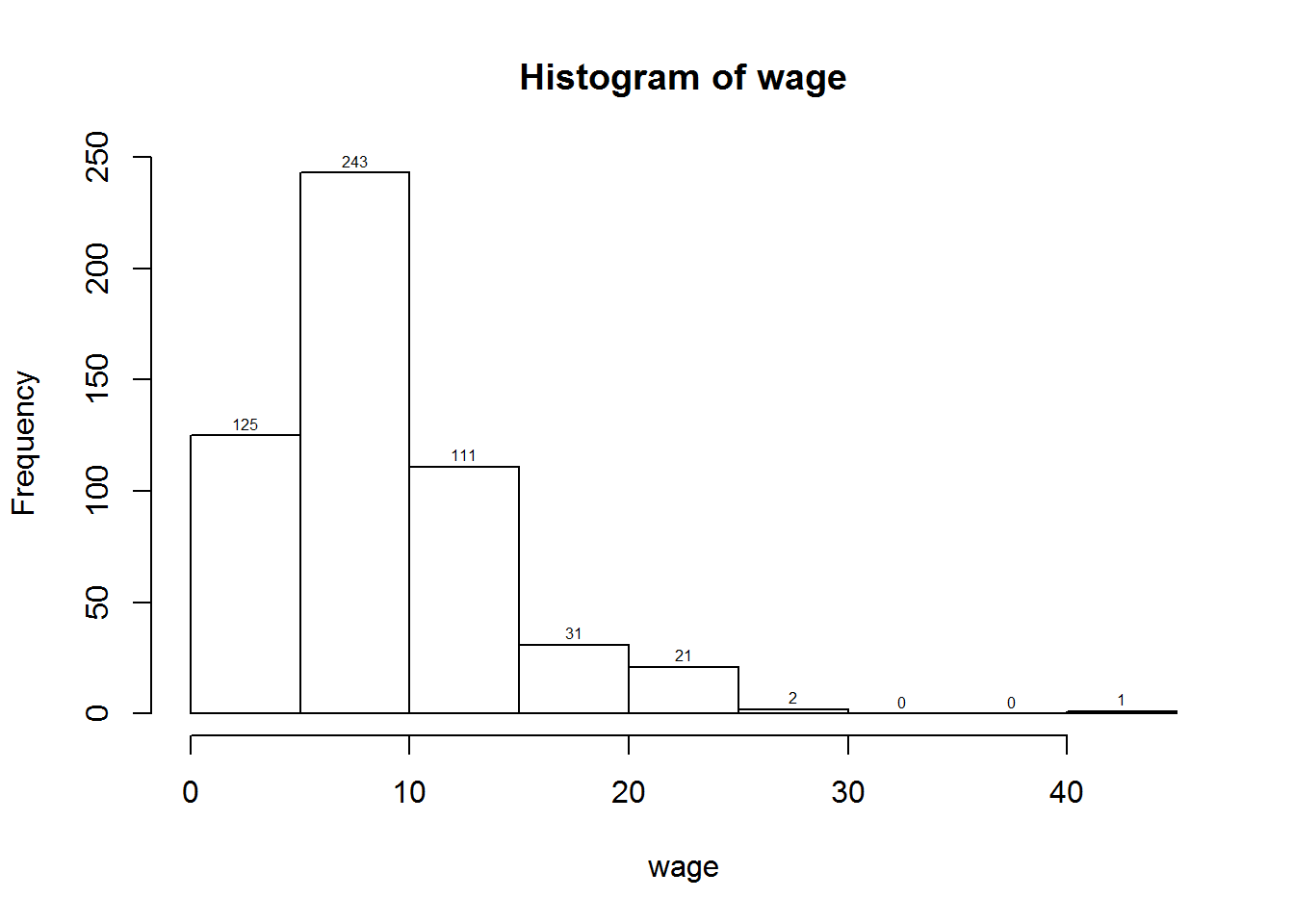
Ahora si, vamos a mejorar el histograma. Pero para ello tenemos que conocer los argumentos de la función hist(). Por tanto, pedimos la ayuda.
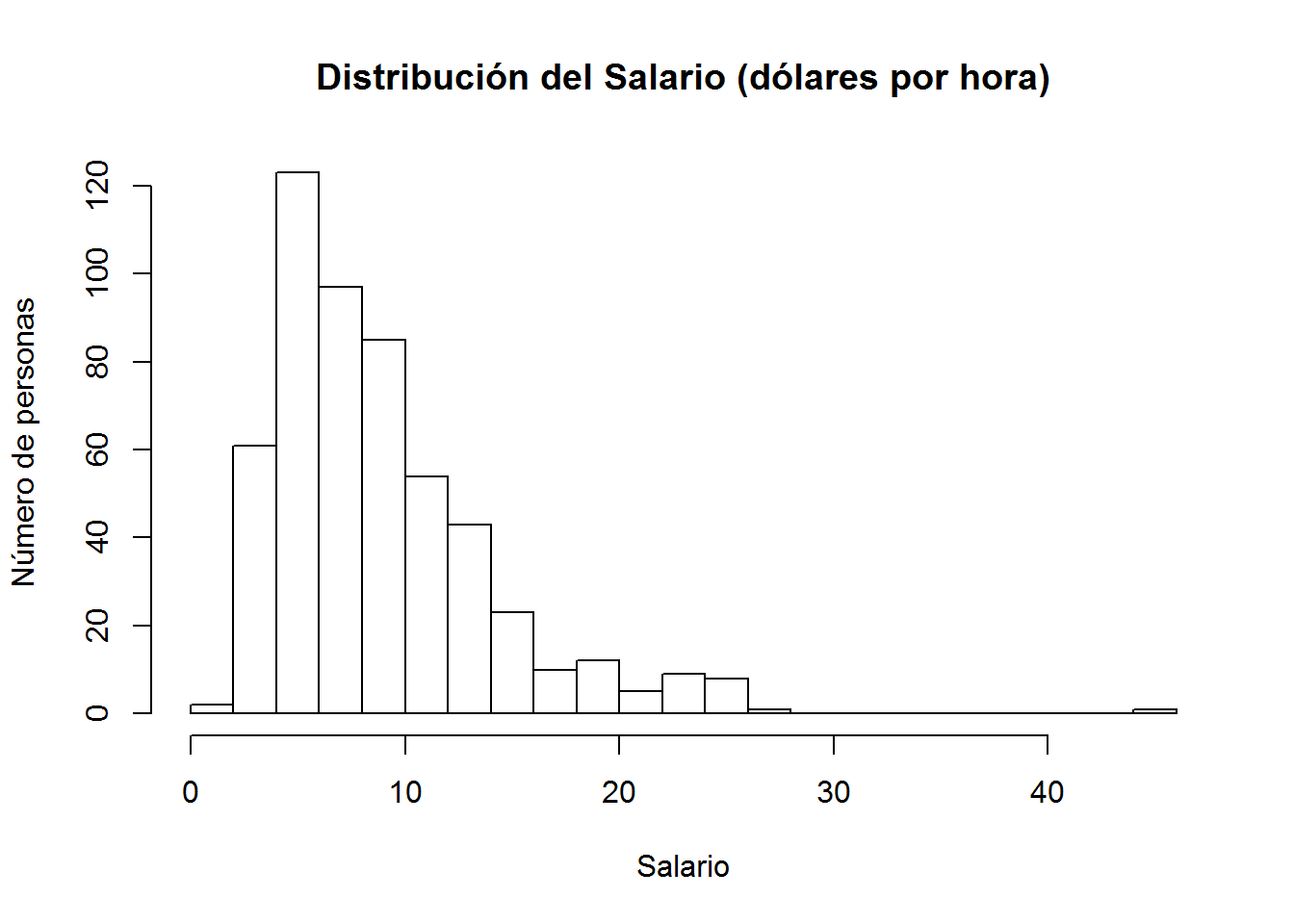
?hist()En primer lugar, para mejorar nuestro histograma, modificamos el número de intervalos (breaks) (se obtiene con la Regla de Sturges, ¡cuánto tiempo sin verlo!). A continuación, escribimos el título del gráfico y rotulamos los ejes.
hist(wage,
breaks = 20, # número de intervalos
main = "Distribución del Salario (dólares por hora)", # título del gráfico
xlab = "Salario", # título del eje x
ylab = "Número de personas" # título del eje y
)
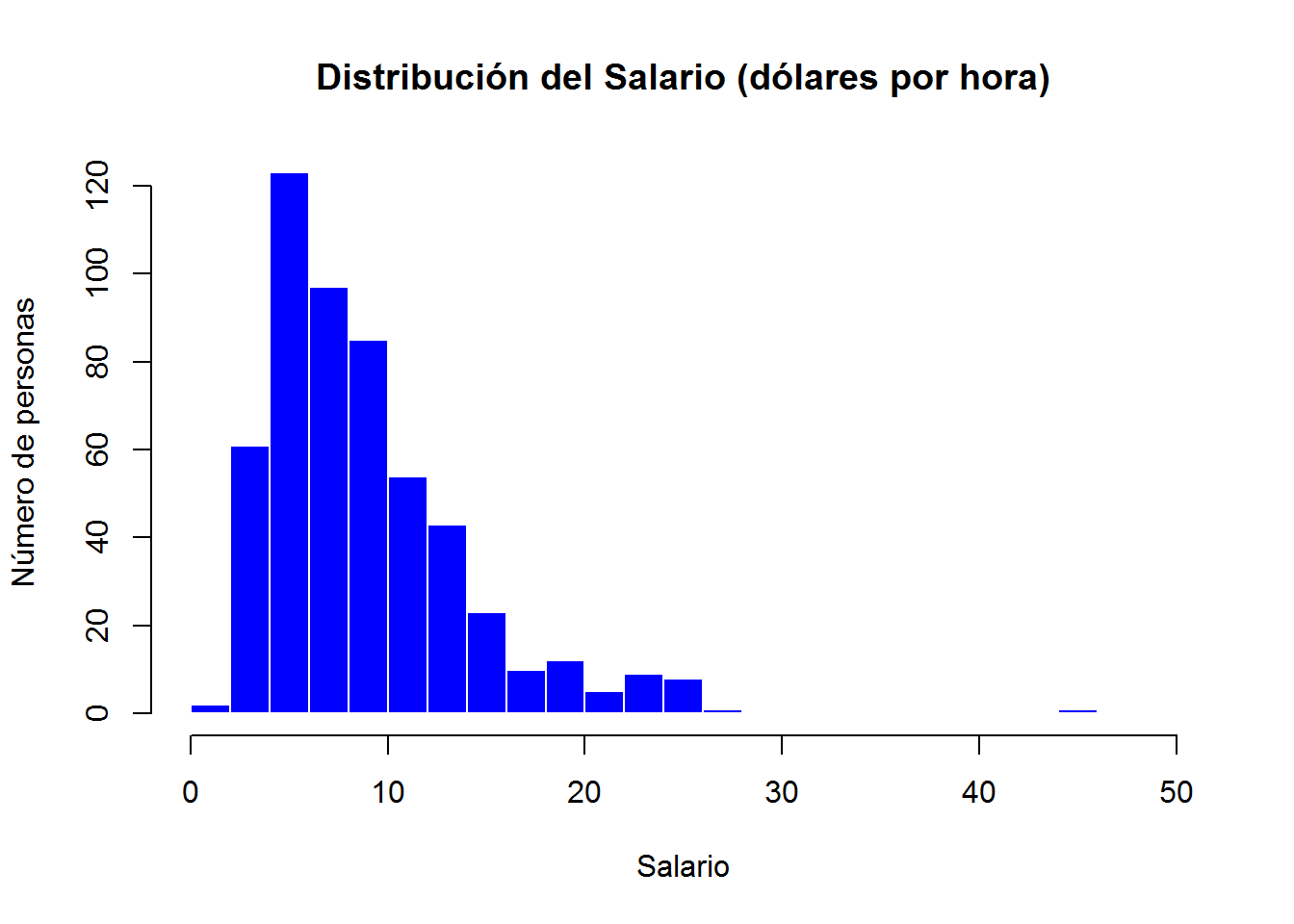
¿Qué más podemos hacer? Por ejemplo, podemos modificar el rango de valores del eje x (y/o del eje y) y colorear el histograma. La paleta de colores que por defecto tiene R se puede consultar ejecutando la función palette(). Para consultar nombres de colores podemos ejecutar en la consola colors() o hacer clic aquí.
hist(wage,
breaks = 20,
main = "Distribución del Salario (dólares por hora)",
xlab = "Salario",
ylab = "Número de personas",
xlim = c(0,50), # rango de valores del eje x
col = "blue", # color de relleno
border = "white" # color del borde del rectángulo
)
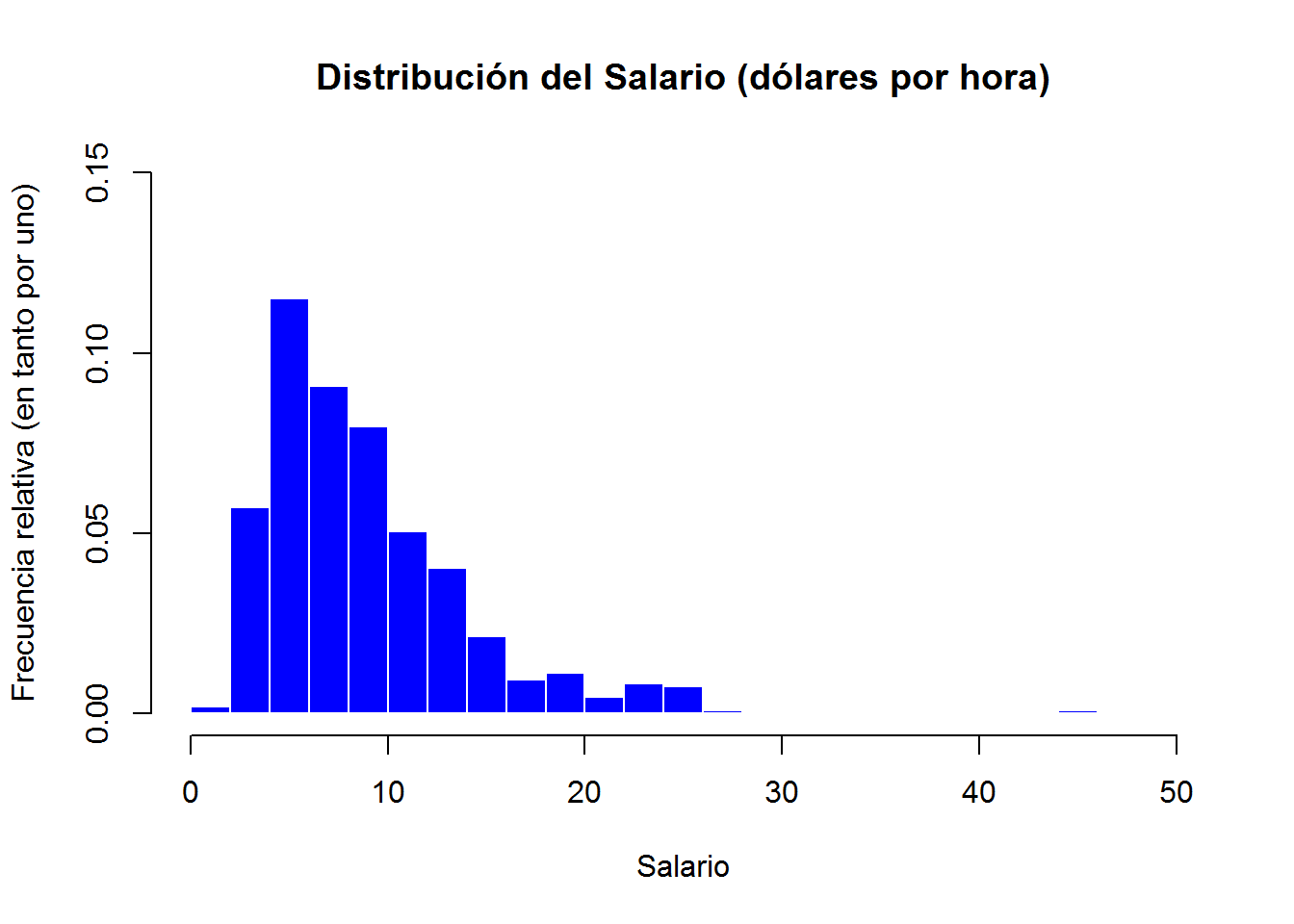
Si en lugar de representar la frecuencia absoluta estamos interesados en representar la frecuencia relativa (probability Density ) tenemos que cambiar el argumento freq de la función hist().
hist(wage,
breaks = 20,
main = "Distribución del Salario (dólares por hora)",
freq = FALSE, # frecuencias relativas (en tanto por uno)
xlab = "Salario",
ylab = "Frecuencia relativa (en tanto por uno)",
xlim = c(0,50),
ylim =c (0,0.15), # cambiamos rango de valores del eje y
col = "blue",
border = "white"
)
En ocasiones, por no decir casi siempre, nos gusta añadir al histograma la curva de la distribución normal; vamos a ver cómo hacerlo.
hist(wage,
breaks = 20,
main = "Distribución del Salario (dólares por hora)",
freq = FALSE,
xlab = "Salario",
ylab = "Frecuencia relativa (en tanto por uno)",
xlim = c(0,50),
ylim = c(0,0.15),
col = "blue",
border = "white"
)
lines(density(wage), col="yellow", lwd=3) # dibujamos la distribución normal empírica con los datos que tenemos
lines(density(wage, adjust=2), col="red", lwd=3, lty=2) # adjust=2 lo que hace es suavizar un poco la curva (probad con adjust=1 y adjust=5 para ver las diferencias).
En el gráfico anterior se han utilizado los argumentos lwd y lty. El primero se refiere al grosor de la línea, el segundo al tipo de línea.
La siguiente gráfica sería una alternativa a la anterior.
hist(wage,
breaks = 20,
main = "Distribución del Salario (dólares por hora)",
freq = FALSE,
xlab = "Salario",
ylab = "Frecuencia relativa (en tanto por uno)",
xlim = c(0,50),
ylim = c(0,0.15),
col = "blue",
border = "white"
)
curve(dnorm(x, mean=mean(wage), sd=sd(wage)), add=TRUE, col="red", lwd=3) # aquí simulamos valores de una normal con la misma media y deviación típica que wage y la representamos.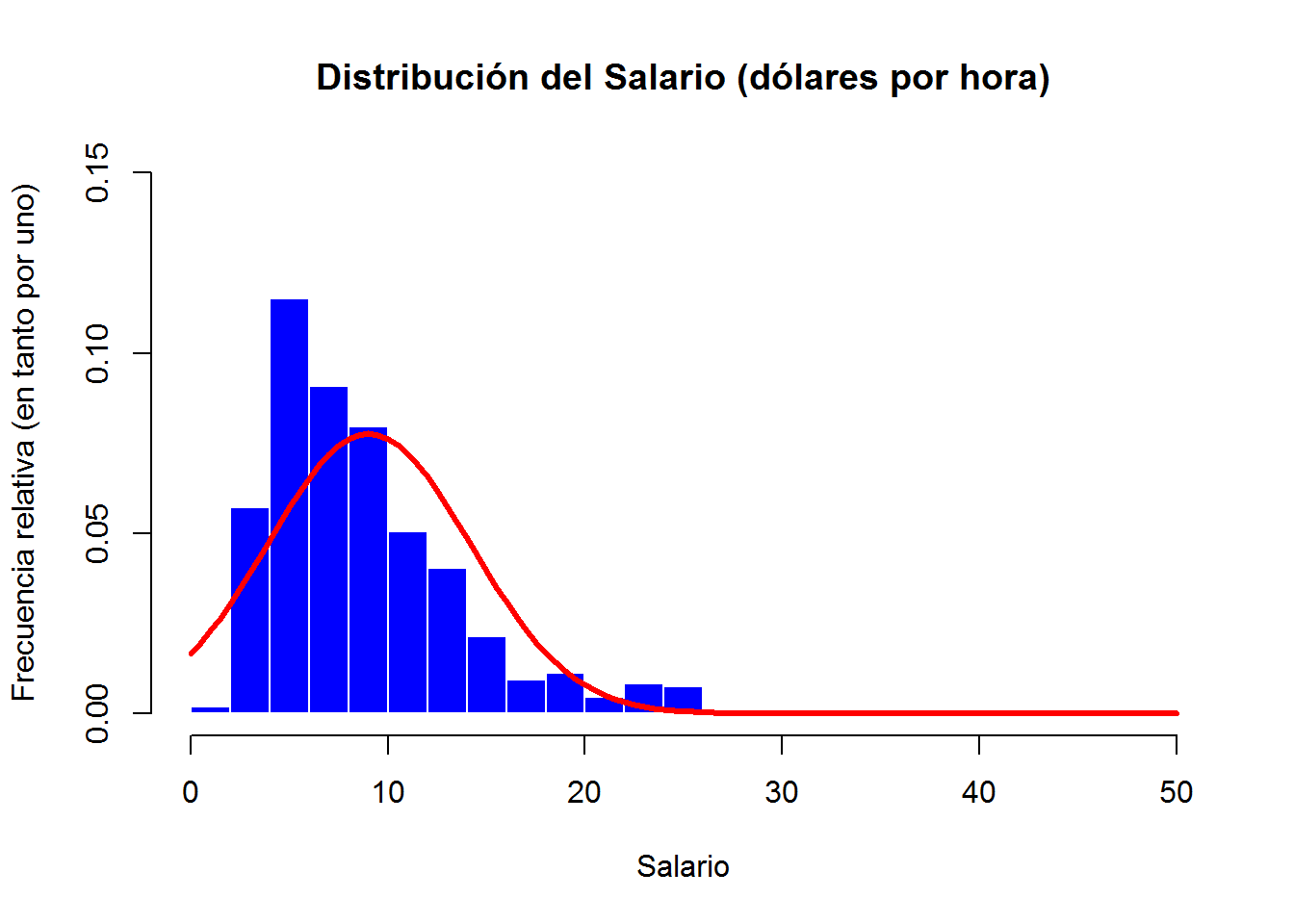
En los gráficos anteriores hemos seleccionado el color (muy básico) para el relleno o para el borde escribiendo directamente el nombre (del color). El tema de los colores es otro universo. Aquí tenéis una cheat sheet de colores. Esta web, o esta otra web, también están bien para orientarnos sobre la selección de (códigos) de colores. Cuando hagamos gráficos con ggplot2 comentaremos el tema de las paletas de colores. Ahora, vamos a replicar nuestro histograma pero seleccionamos un color mediante su código Hex.
hist(wage,
breaks = 20,
main = "Distribución del Salario (dólares por hora)",
freq = FALSE,
xlab = "Salario",
ylab = "Frecuencia relativa (en tanto por uno)",
xlim = c(0,50),
ylim = c(0,0.15),
col = "#ff9900",
border = "#0040ff"
)
curve(dnorm(x, mean=mean(wage), sd=sd(wage)), add=TRUE, col="#00ff00", lwd=3)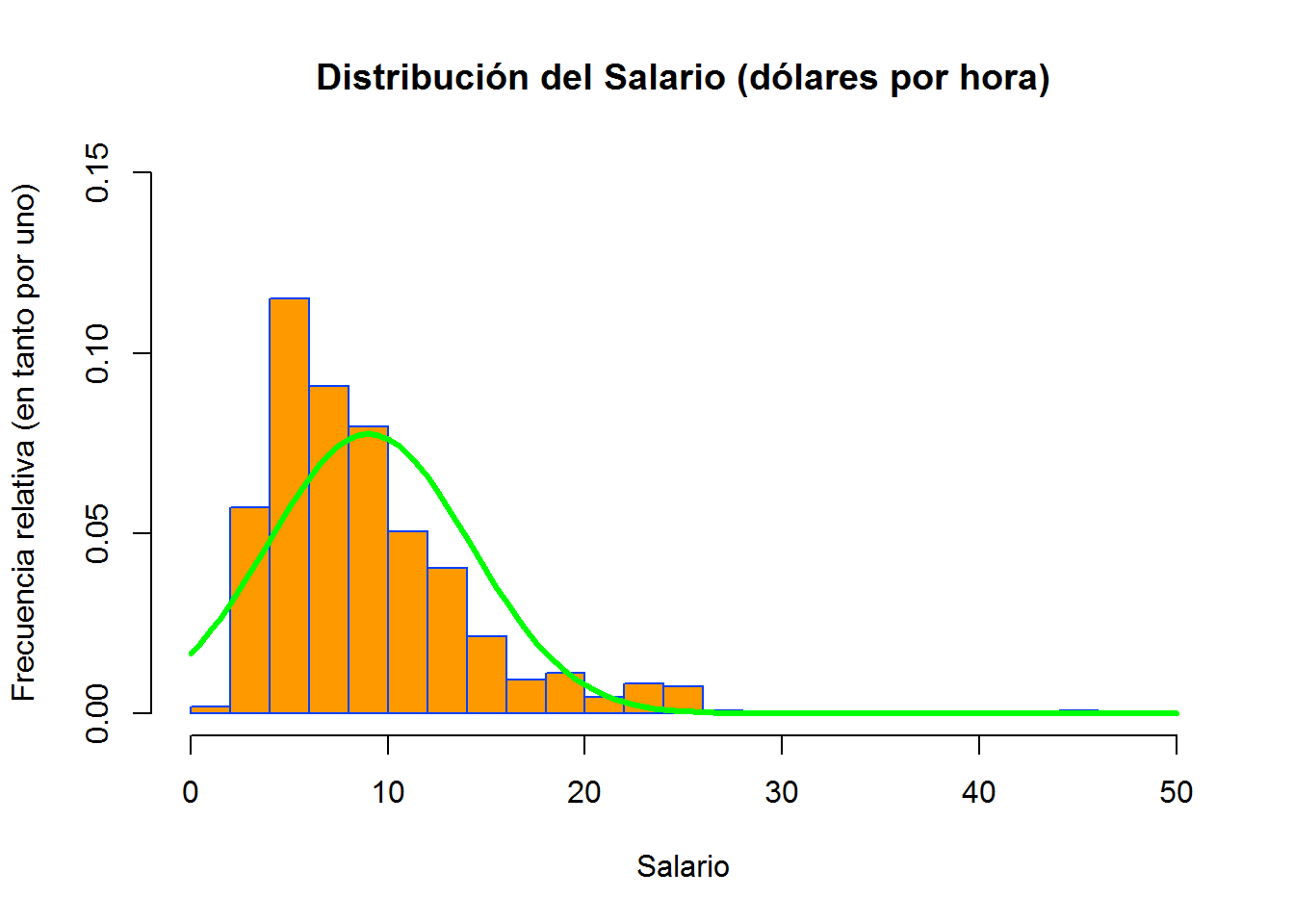
Por último, tal vez estemos interesados en indicar/señalar la posición de la media (o cualquier otra medida) en el histograma. Para hacer esto utilizamos la función abline().
hist(wage,
breaks = 20,
main = "Distribución del Salario (dólares por hora)",
freq = FALSE,
xlab = "Salario",
ylab = "Frecuencia relativa (en tanto por uno)",
xlim = c(0,50),
ylim = c(0,0.15),
col = "#ff9900",
border = "#0040ff"
)
curve(dnorm(x, mean=mean(wage), sd=sd(wage)), add=TRUE, col="#00ff00", lwd=3)
abline(v=mean(wage), lwd=2, lty=3, col="darkblue") # añadimos posición de la media. Recordemos que e argumento "lwd"" hace referencia al grosor de la línea y "lty"" al tipo de línea.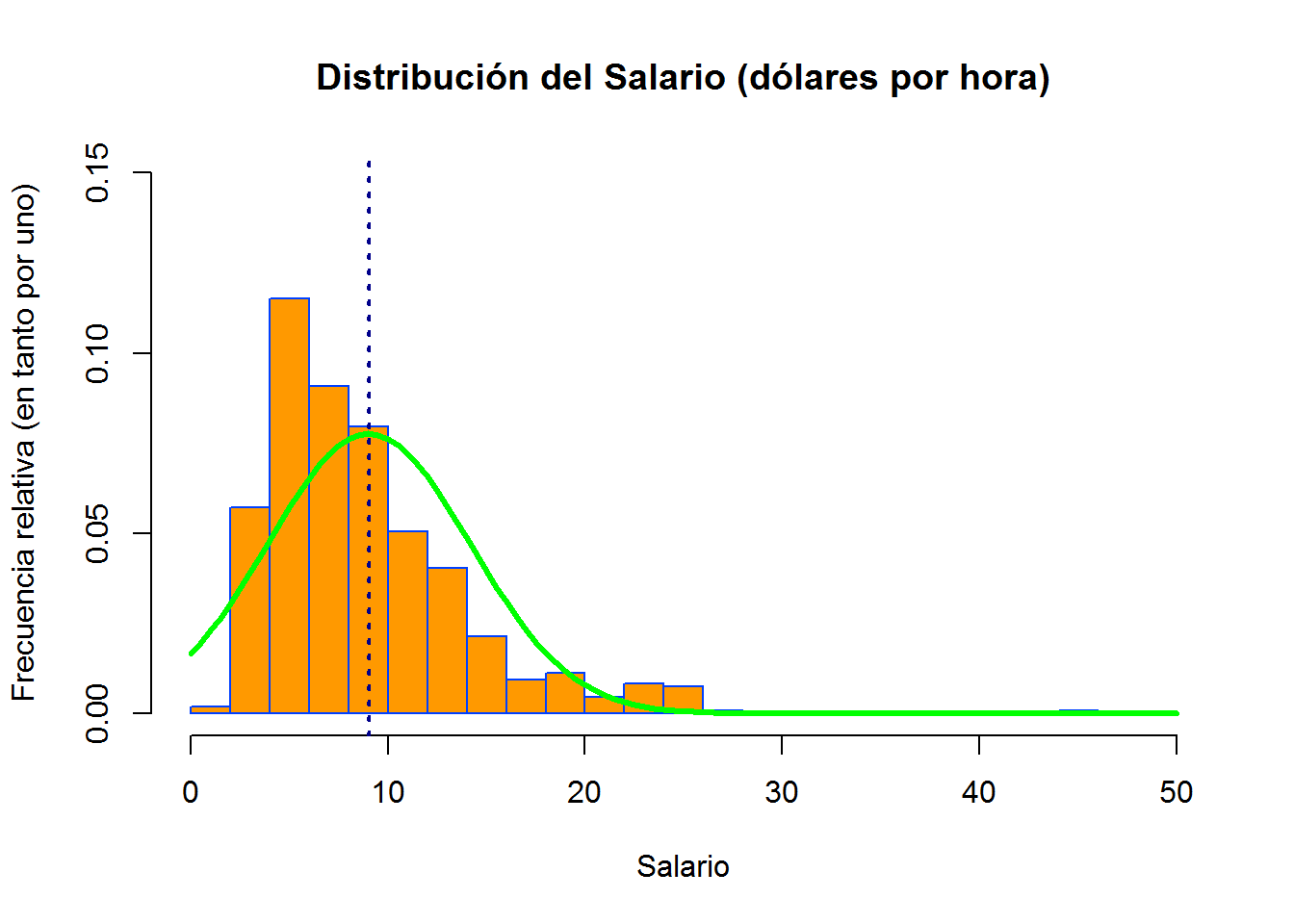
¿Suficiente para un curso introductorio?
Es momento de practicar lo aprendido. Ahí van dos tareas…
- Tarea 1. Dibujad un histograma para ver la distribución de la experiencia (experience).
- Tarea 2. Cread una nueva variable, log(wage), que sea el logaritmo del salario (wage). Dibujad el histograma de log(wage) y compararlo con el histograma de la variable original wage. ¿Qué conclusión puede extraerse?
Boxplot (diagrama de Caja y Bigotes)
En los gráficos Boxplot (o Box and Whiskers, más conocidos como Caja y Bigotes) se representan los cinco números (mínimo, cuartil 1, mediana, cuartil 3 y máximo), lo que nos puede ayudar a hacernos una idea de la asimetría de la distribución. Los gráficos de Caja y Bigotes también permiten detectar valores atípicos y outliers.
La función para representar los diagramas de Caja y Bigotes es boxplot(). Como siempre, es recomendable echar un vistazo a los argumentos de la función.
?boxplot # recordad que también podemos escribir en la consola el nombre de la función y pulsar la tecla F1.Vamos a hacer el boxplot de la variable wage.
boxplot(wage)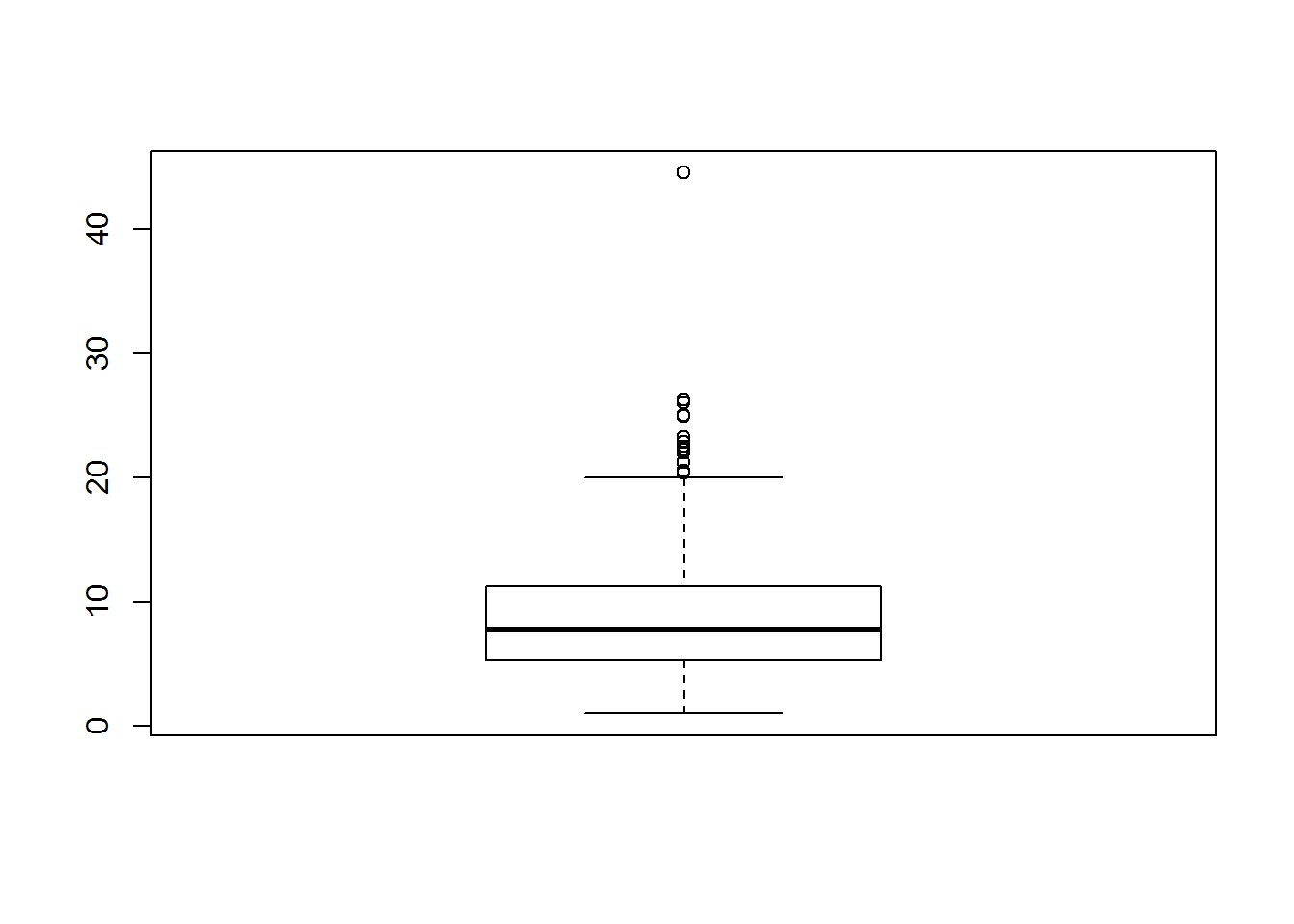
Hay va la pregunta habitual… ¿Qué podemos hacer para mejorar este gráfico?
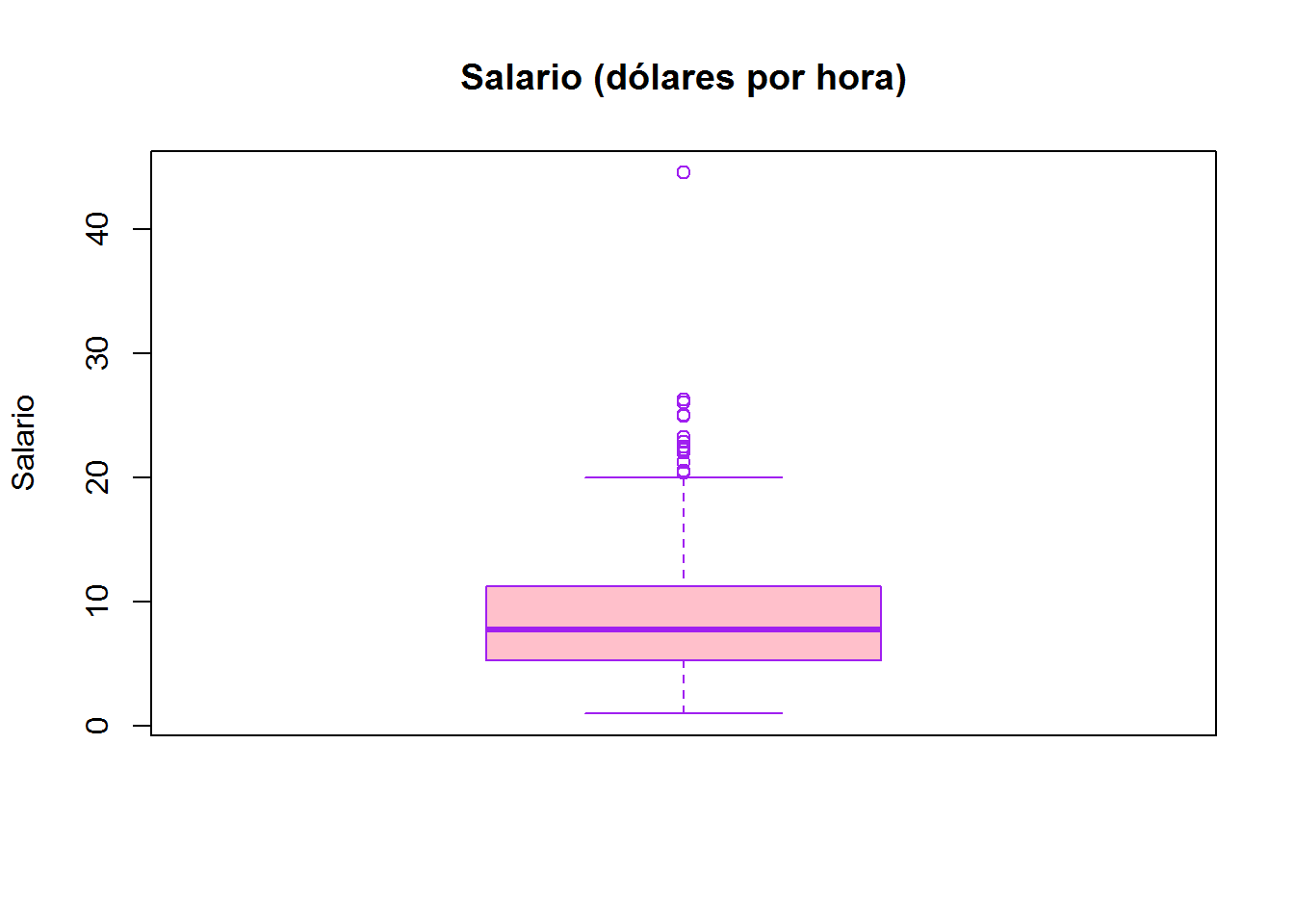
Podemos incluir el título principal del gráfico, el nombre de la variable que estamos representando, colorear la caja y los bordes… (Recordad la hoja o la función donde podemos encontrar los nombres de colores).
boxplot(wage,
main = "Salario (dólares por hora)",
ylab = "Salario",
col = "pink",
border = "purple"
)
¿Cómo son los salarios de hombres y mujeres? Vamos a ver su distribución en un boxplot (básico).
boxplot(wage ~ gender)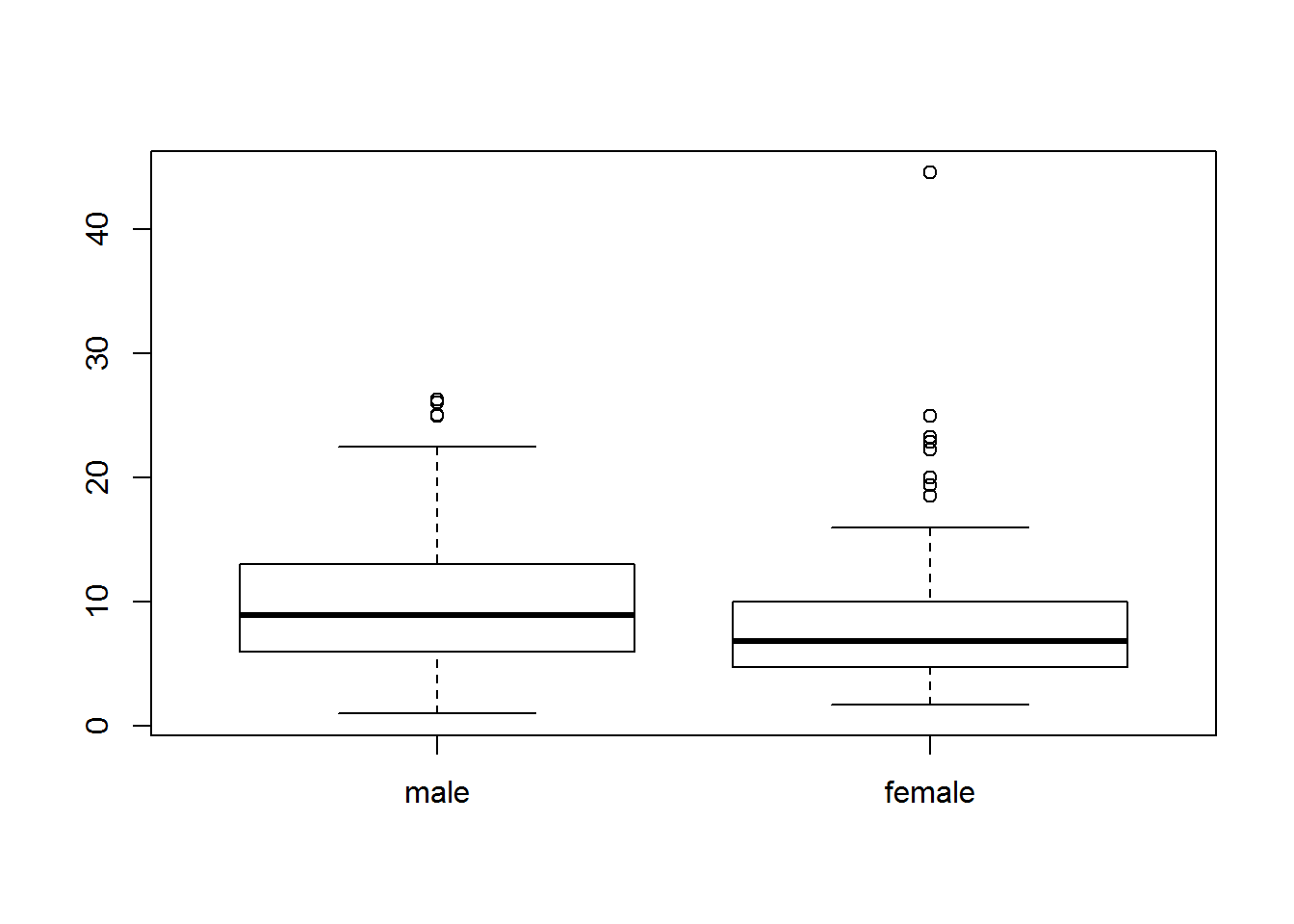
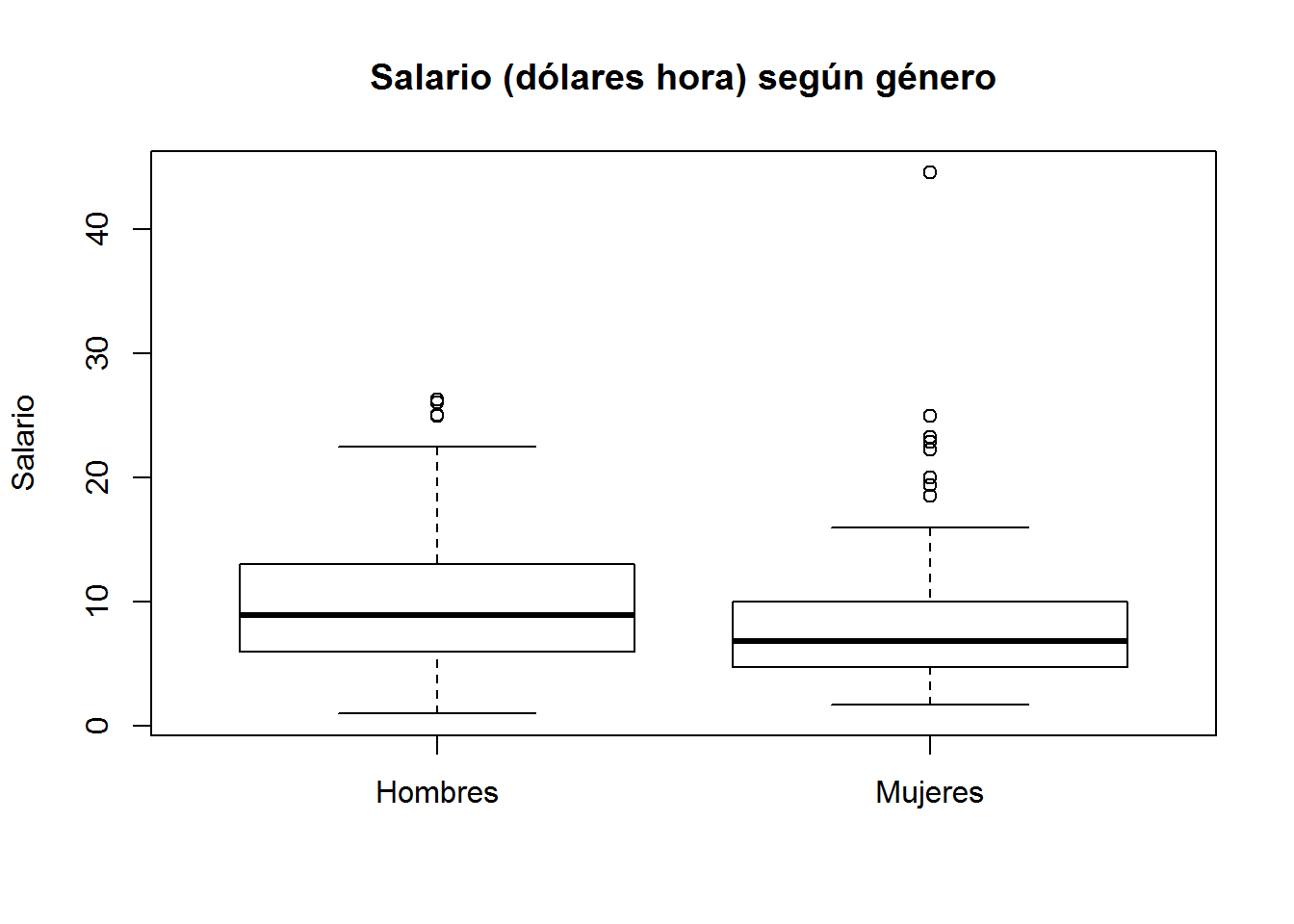
Incluimos el título del gráfico e información sobre las variables que estamos representando.
boxplot(wage ~ gender,
main = "Salario (dólares hora) según género",
ylab = "Salario",
names = c("Hombres","Mujeres") # cambiamos la etiqueta de la variable cualitativa
)
Muchos colegas prefieren presentar el boxplot en horizontal (¡igual ya me lo habéis preguntado!). También resulta muy ilustrativo incluir la media de salario según género. Para hacer esto último utilizamos la función points().
datos_mujeres <- subset(CPS1985, gender=="female") # seleccionamos los datos de las mujeres
datos_hombres <- subset(CPS1985, gender=="male") # seleccionamos los datos de los hombres
boxplot(wage ~ gender,
main = "Salario (dólares hora) según género",
ylab = "Salario",
names = c("Hombres","Mujeres"),
horizontal = T # boxplot en posición horizontal
)
points(mean(datos_hombres$wage), 1, pch=25, bg="red") # incluimos salario medio de hombres
points(mean(datos_mujeres$wage), 2, pch=22, bg="blue") # incluimos salario medio de mujeres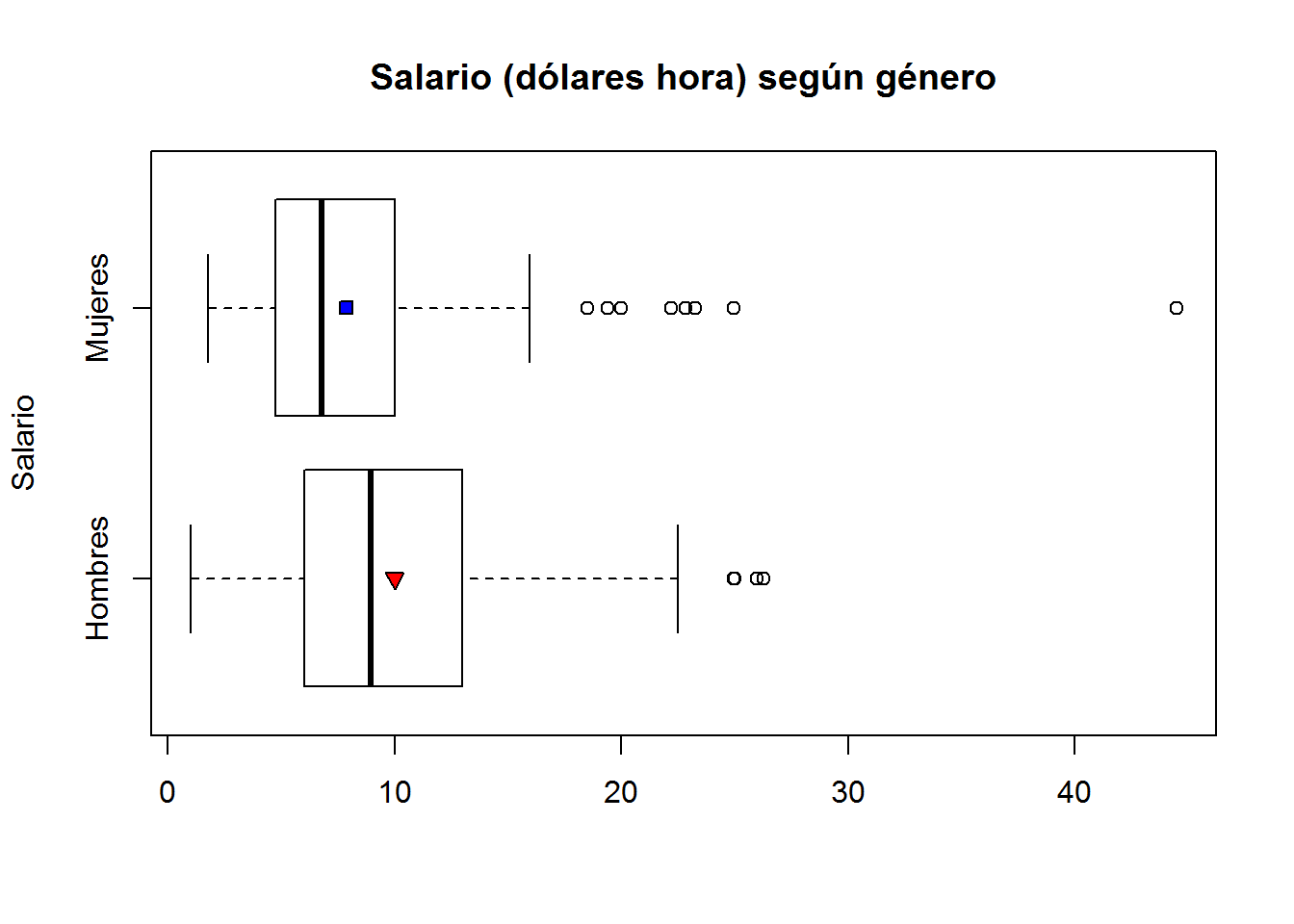
Para colorear el diagrama de Caja y Bigotes vamos a utilizar las paletas de colores (bueno, las paletas se utilizan para cualquier gráfico). Aquí podéis encontrar una Cheat sheet sobre este tema. Paletas de colores hay muchas, pero de las más utilizadas son:
- rainbow
- colorspace
- RColorBrewer (ver más aquí)
Para gráficos sencillos también se utilizan las paletas topo.colors, cm.colors, heat.colors o terrain.colors. Nosotros mismos podemos definir nuestra propia paleta (hacer clic aquí para ver cómo hacerlo).
Veamos el efecto de algunas de las paletas a las que se ha hecho referencia.
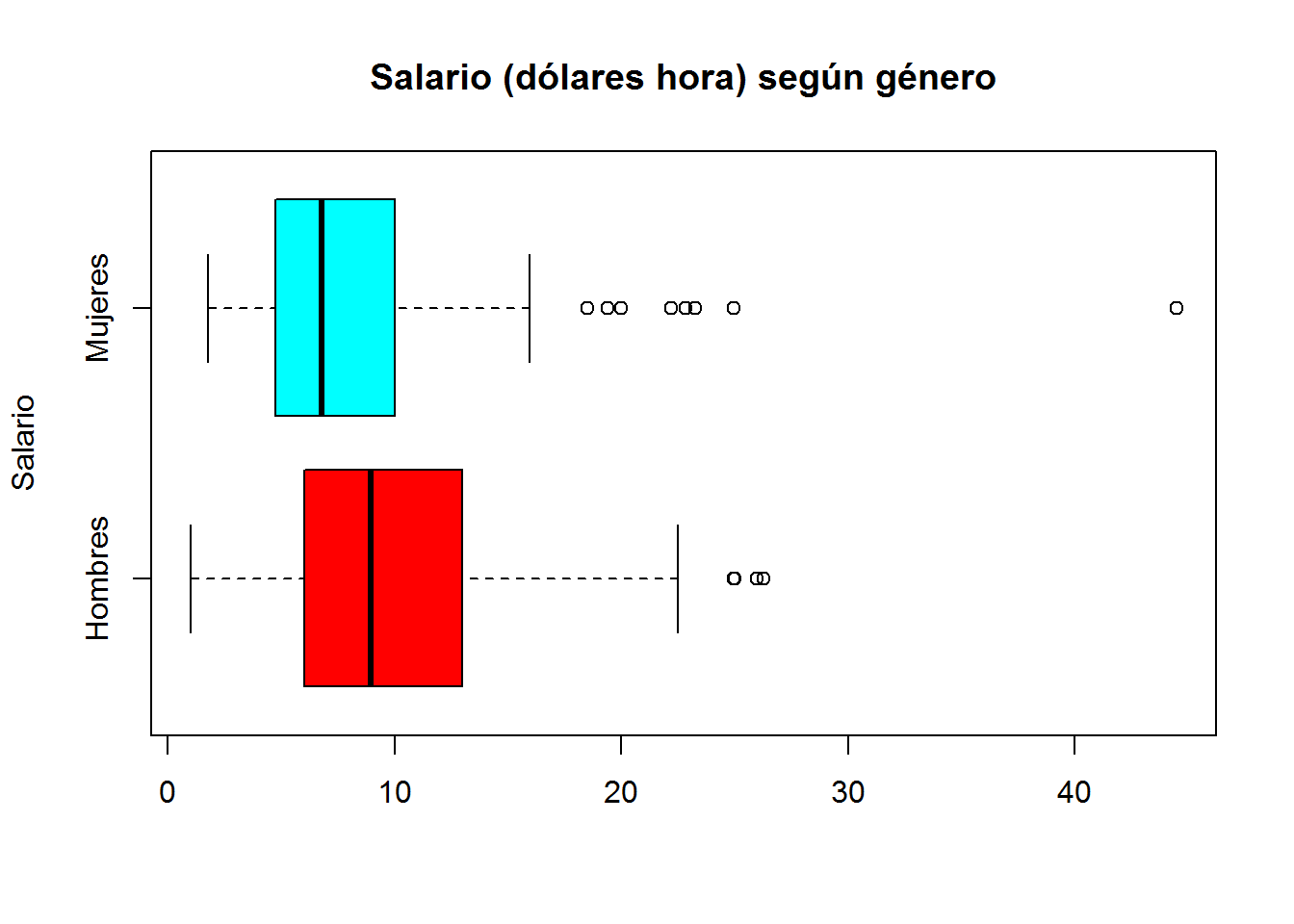
- Con rainbow
boxplot(wage ~ gender,
main = "Salario (dólares hora) según género",
ylab = "Salario",
names = c("Hombres","Mujeres"),
horizontal = T,
col = rainbow(2) # el número hace referencia al número de colores a utilizar
# introducir el algumento alpha (entre 0 y 1) para transperencias de color. Observar los cambios
)
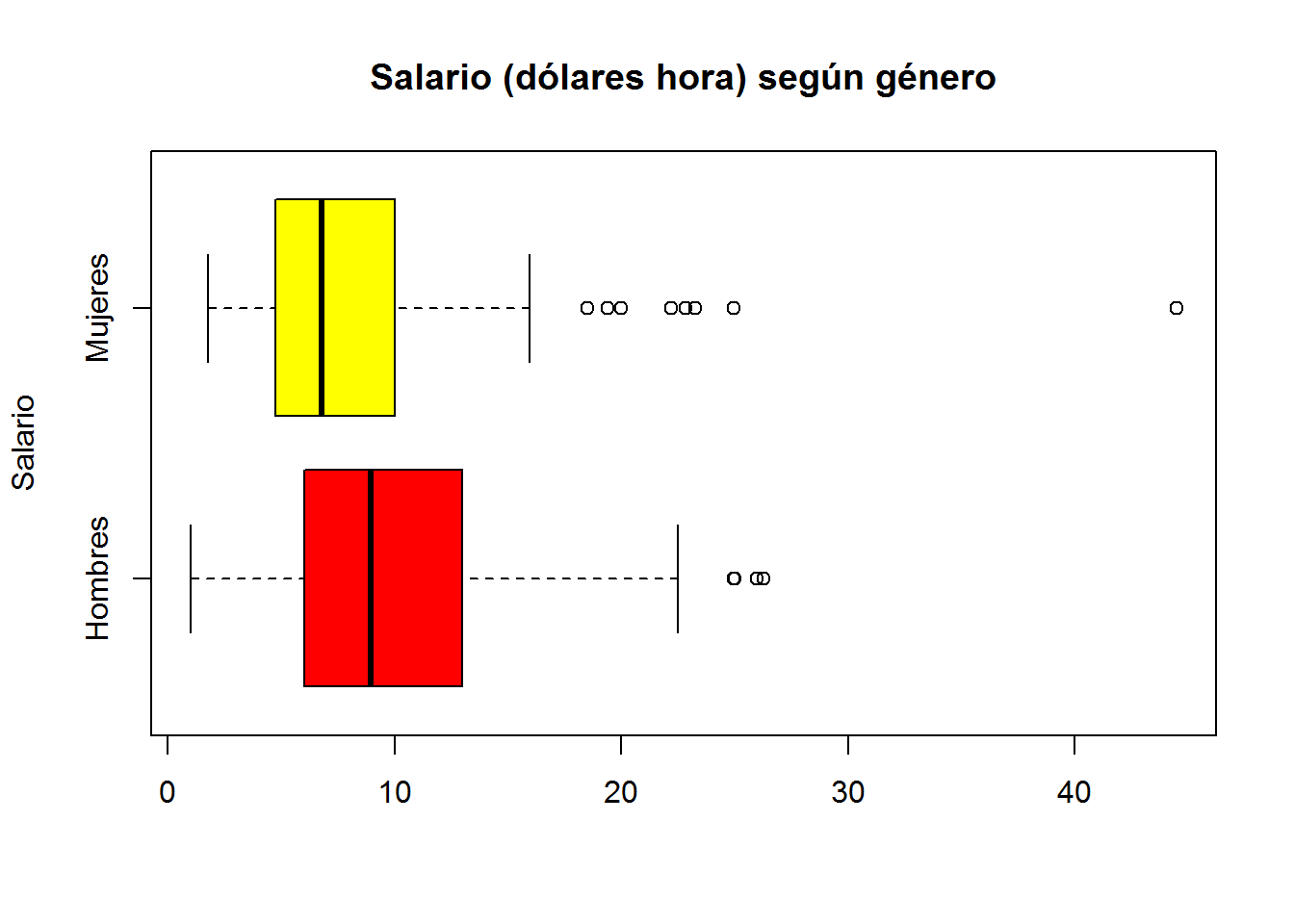
- Con heat.colors
boxplot(wage ~ gender,
main = "Salario (dólares hora) según género",
ylab = "Salario",
names = c("Hombres","Mujeres"),
horizontal = T,
col = heat.colors(2)
)
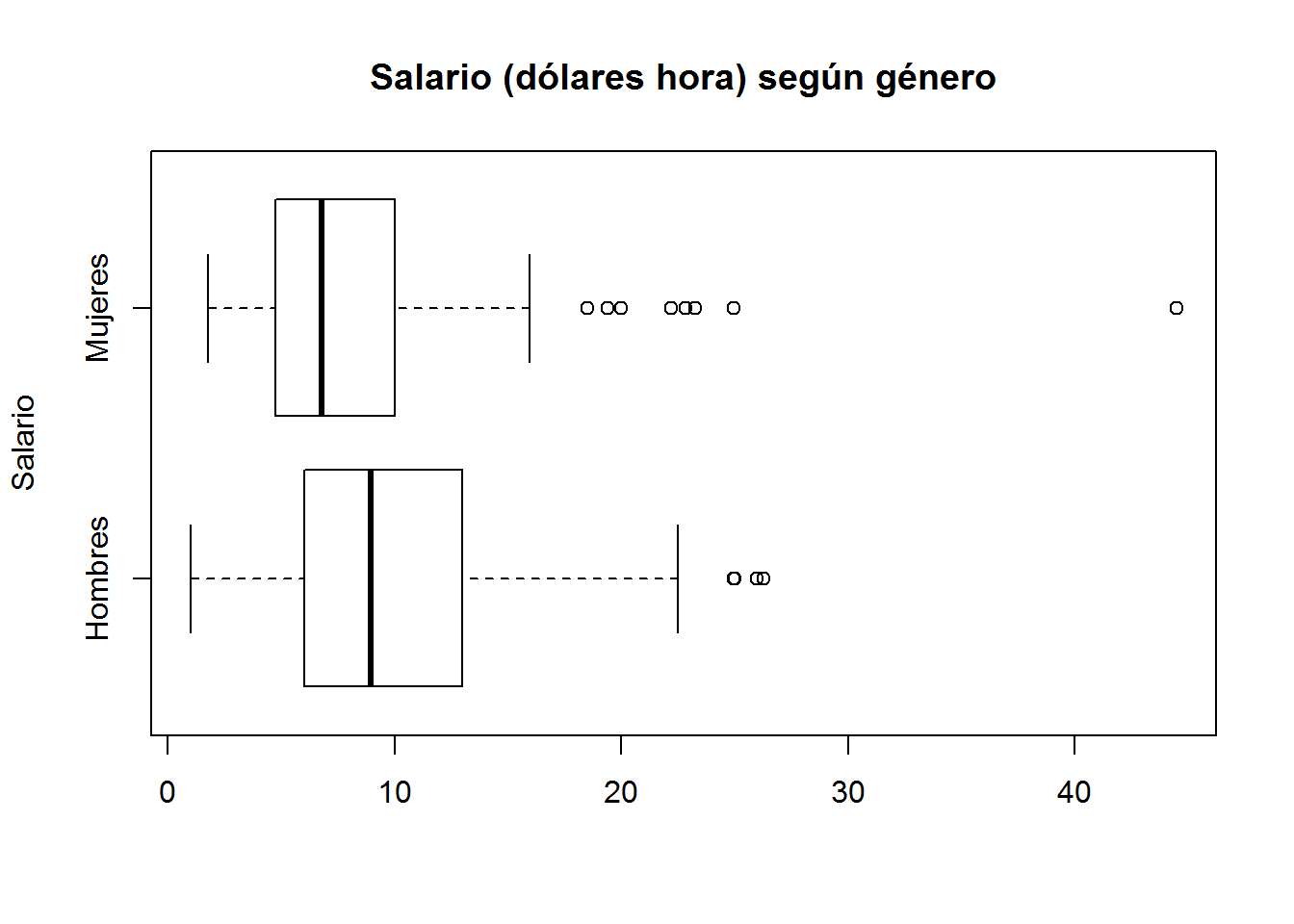
- Con colorspace. Para utilizar la paleta colorspace, primero hemos de cargar la librería y después seleccionamos la paleta que queremos. Finalmente, cargamos nuestra selección.
library(colorspace)
#pal <- choose_palette(diverge_hcl) # para seleccionar la paleta que queremos
boxplot(wage ~ gender,
main = "Salario (dólares hora) según género",
ylab = "Salario",
names = c("Hombres","Mujeres"),
horizontal = T,
#col = pal(2) # seleccionamos 2 colores de la paleta elegida
)
Tal vez no hayamos percibido el efecto de las paletas porque hemos representado el salario (wage) en función de una variable categórica que solo tenía dos categorías (gender). Realizar la siguiente tarea.
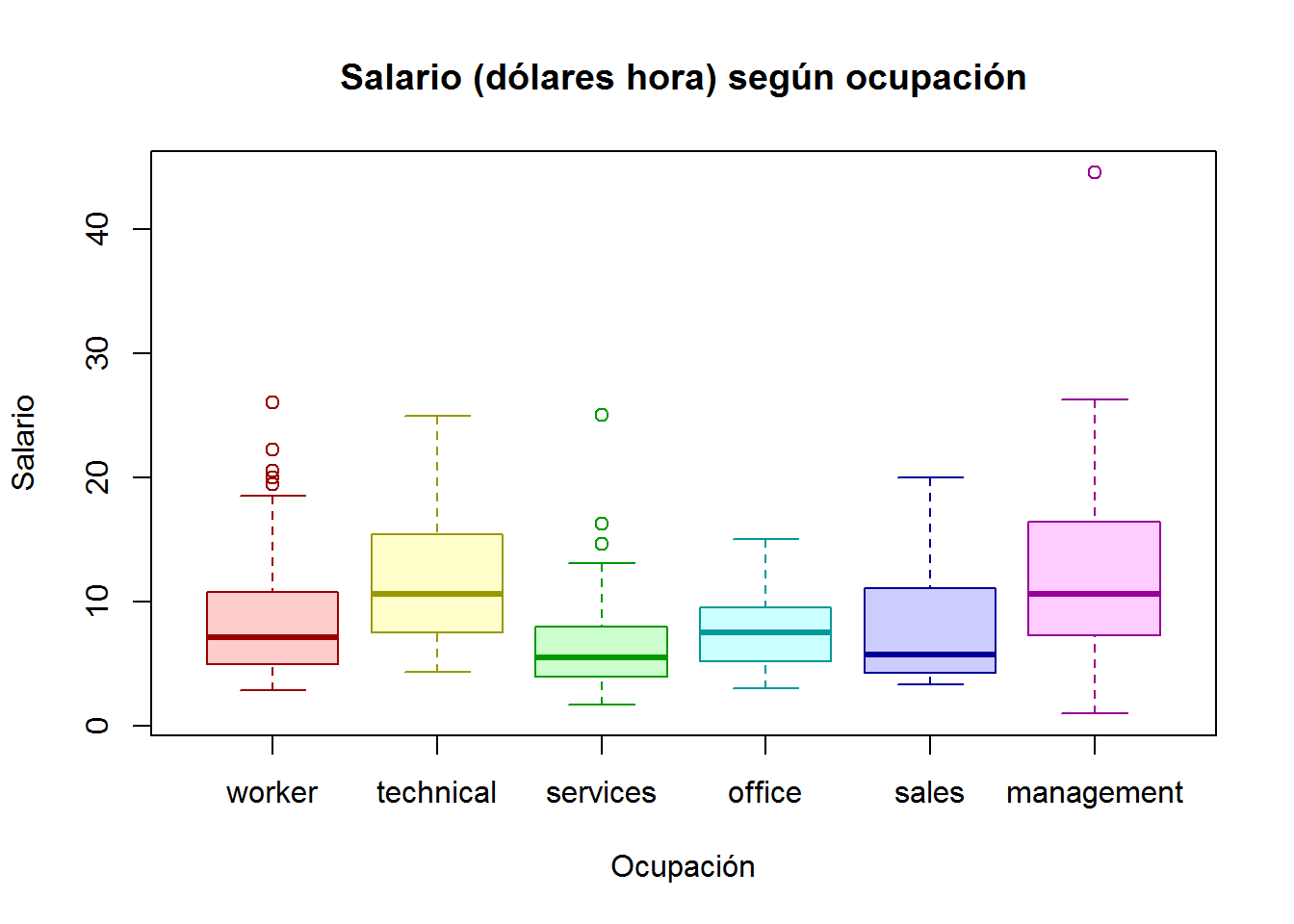
- Tarea. Utilizando un boxplot, representar el salario (wage) en función de la ocupación (occupation). Incorporad al gráfico toda la información que se considere oportuna y utilizad distintas paletas de colores para ver los efectos.
boxplot(wage ~ occupation,
main = "Salario (dólares hora) según ocupación",
ylab = "Salario",
xlab = "Ocupación",
col = rainbow(6, alpha=0.2),
border = rainbow(6, v=0.6)
)
Con lo que hemos visto hasta ahora de gráficos, podemos darnos cuenta que en R tenemos realmente control sobre todos los elementos que componen el gráfico. Para un ejemplo, observemos los detalles del siguiente boxplot (basado en este post).
a <- rainbow(6)
b <- rainbow(6, alpha=0.2)
c <- rainbow(6, v=0.5)
boxplot(wage ~ occupation,
col = b, # color de relleno de la caja
boxcol = c, # color del borde de la caja
medcol = c, # color de la mediana (línea dentro de la caja)
whiskcol = a, # color de los bigotes
staplecol = c, # color de las líneas finales de los bigotes
outcol = c, # color de los puntos (atípicos y outliers)
outbg = c, # relleno de los puntos
pch = 20, # forma de los puntos
cex = 1, # tamaño de los puntos
horizontal = T, # cambiamos la posición de los diagramas a horizontal
main = "Salario (dólares hora) según ocupación",
ylab = "Ocupación",
xlab = "Salario"
)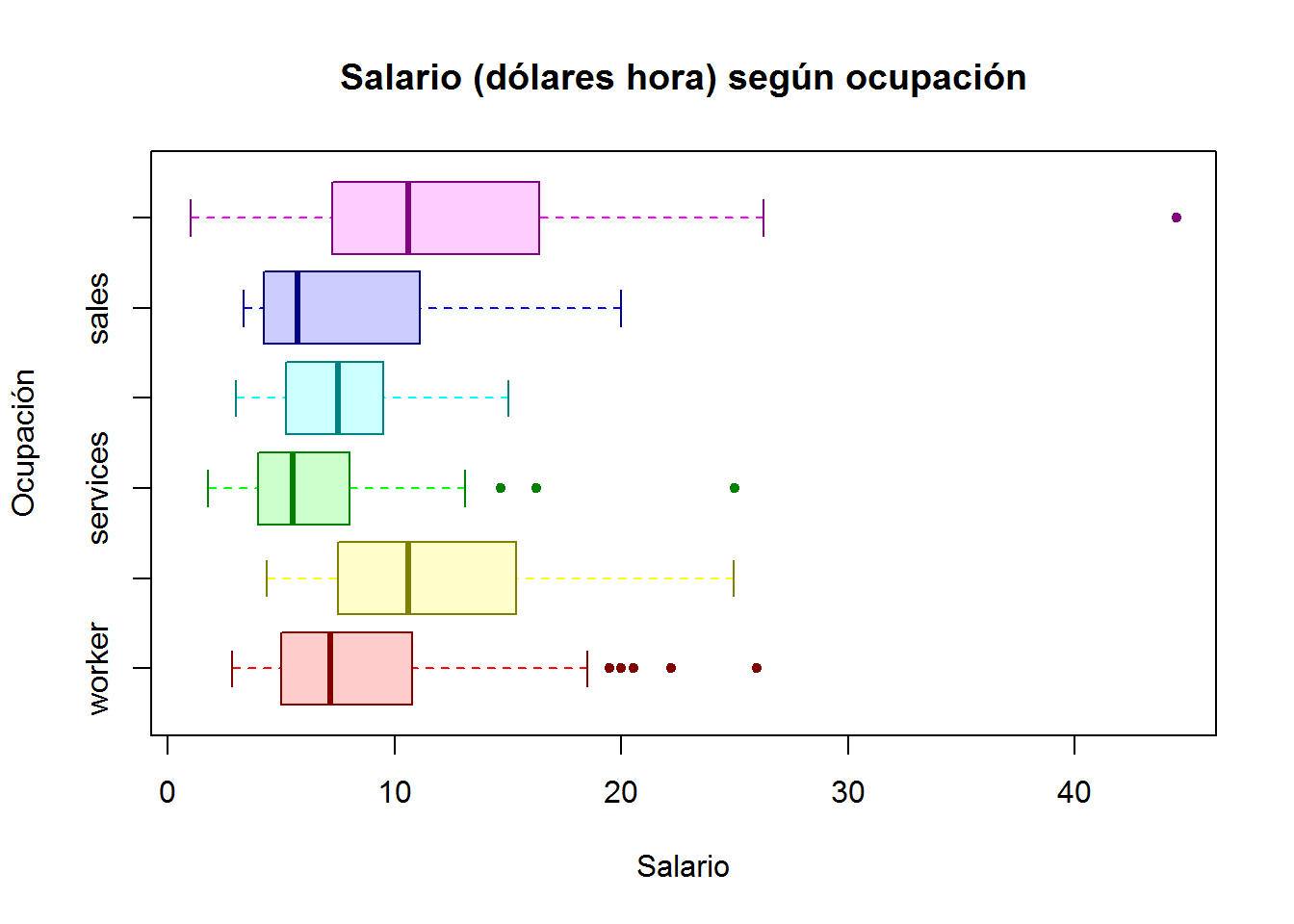
Como vemos, al cambiar la orientación del gráfico se originan ciertos problemas de visualización. Debemos modificar los márgenes. Esta Cheat sheet es una buena ayuda para modificar los parámetros re
opar <- par() # guardamos los parámetros por defecto
par(mar=c(5,6,4,2)) # modificamos los márgenes (inferios, izquierdo, superior, derecho)
a <- rainbow(6)
b <- rainbow(6, alpha=0.2)
c <- rainbow(6, v=0.5)
boxplot(wage ~ occupation,
col = b,
boxcol = c,
medcol = c,
whiskcol = a,
staplecol = c,
outcol = c,
outbg = c,
pch = 20,
cex = 1,
horizontal = T,
main ="Salario (dólares hora) según ocupación",
xlab = "Salario",
ylim = c(0,50), # ampliamos el rango del eje
las = 1, # cambiamos la orientación de las etiquetas
frame = F # eliminamos el marco del gráfico
)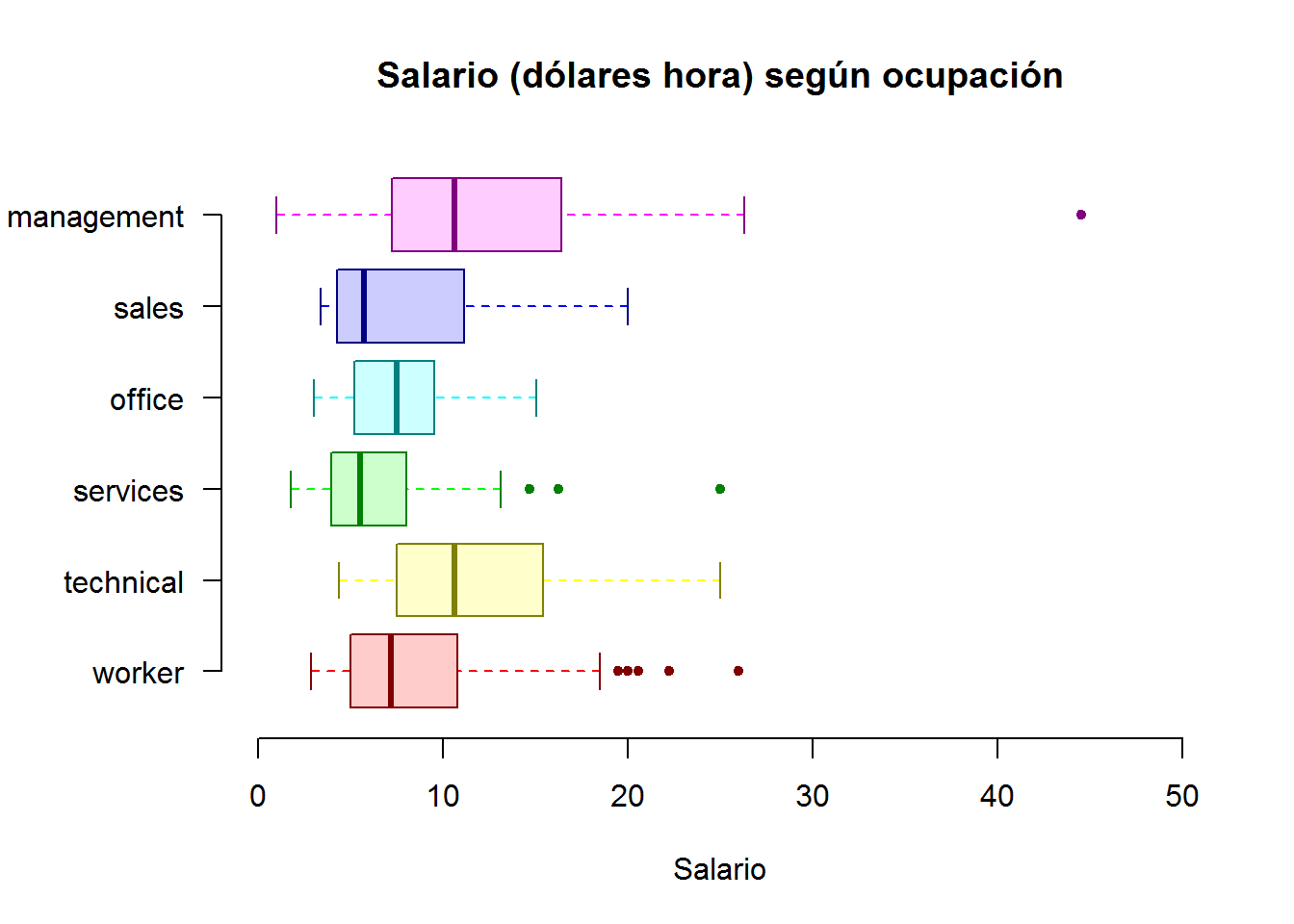
par(opar) # volvemos a los parámetros originalesOtra opción sería hacer referencia a las categorías de ocupación en una leyenda anexa al gráfico. Por ejemplo:
a <- rainbow(6)
b <- rainbow(6, alpha=0.2)
c <- rainbow(6, v=0.5)
boxplot(wage ~ occupation,
col = b,
boxcol = c,
medcol = c,
whiskcol = a,
staplecol = c,
outcol = c,
outbg = c,
pch = 20,
cex = 1,
horizontal = T,
main = "Salario (dólares hora) según ocupación",
xlab = "Salario",
yaxt = "n" # elminamos el eje y
)
legend("bottomright", title="Salario (dólares hora)", levels(occupation), fill=b)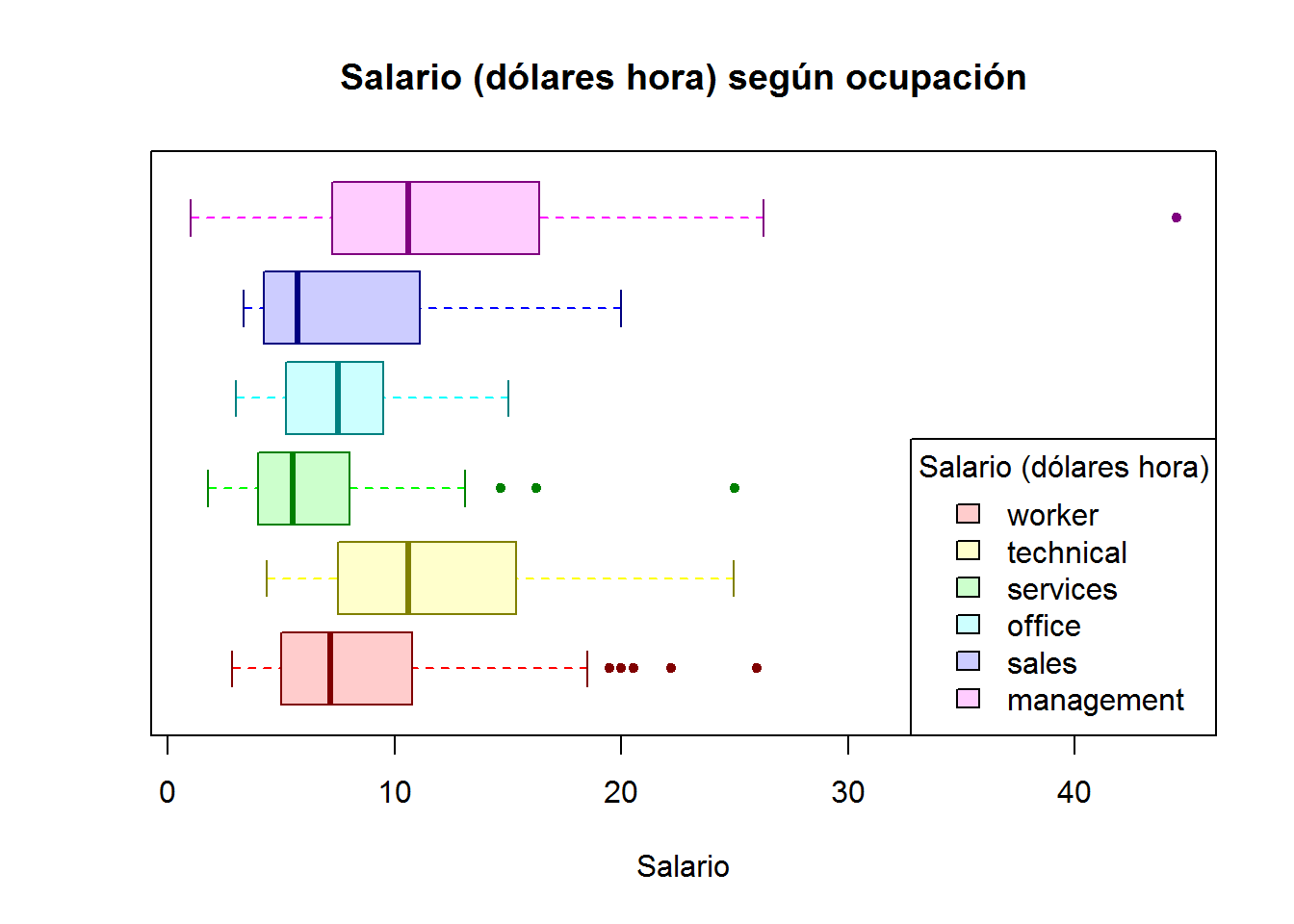
Diagrama de dispersión.
Los diagramas de dispersión permiten efectuar un diagnóstico visual de la posible relación (funcional) entre dos variables de naturaleza cuantitativa. La función que permite realizar este tipo de gráfico es plot(). Si solicitamos la ayuda de R sobre esta función (?plot), veremos que la función plot tiene un argumento llamado type que sirve para seleccionar el tipo de gráfico a dibujar. Las opciones de type son:
- “p” para hacer un gráfico de puntos (es el tipo de gráfico por defecto).
- “l” para hacer un gráfico de líneas.
- “b” para hacer un gráfico de puntos y líneas (pero las líneas no entran en los puntos).
- “c” para hacer un gráfico de líneas (parten de los puntos, sin entrar, pero no se representan).
- “o” para hacer un gráfico de puntos y líneas (ahora las líneas entran en los puntos).
- “h” para hacer un histograma o un diagrama de barras.
- “s” para hacer un diagrama de escalera.
Por defecto la opción plot es type=p. Por tanto, si queremos hacer un diagrama de dispersión para representar la nube de puntos no será necesario indicar el tipo de gráfico.
Como la variable Salario presenta una importante dispersión y asimetría (ver histograma), vamos a representar el logaritmo del salario (log(wage)) en función de la experiencia (experience).
plot (experience, log(wage))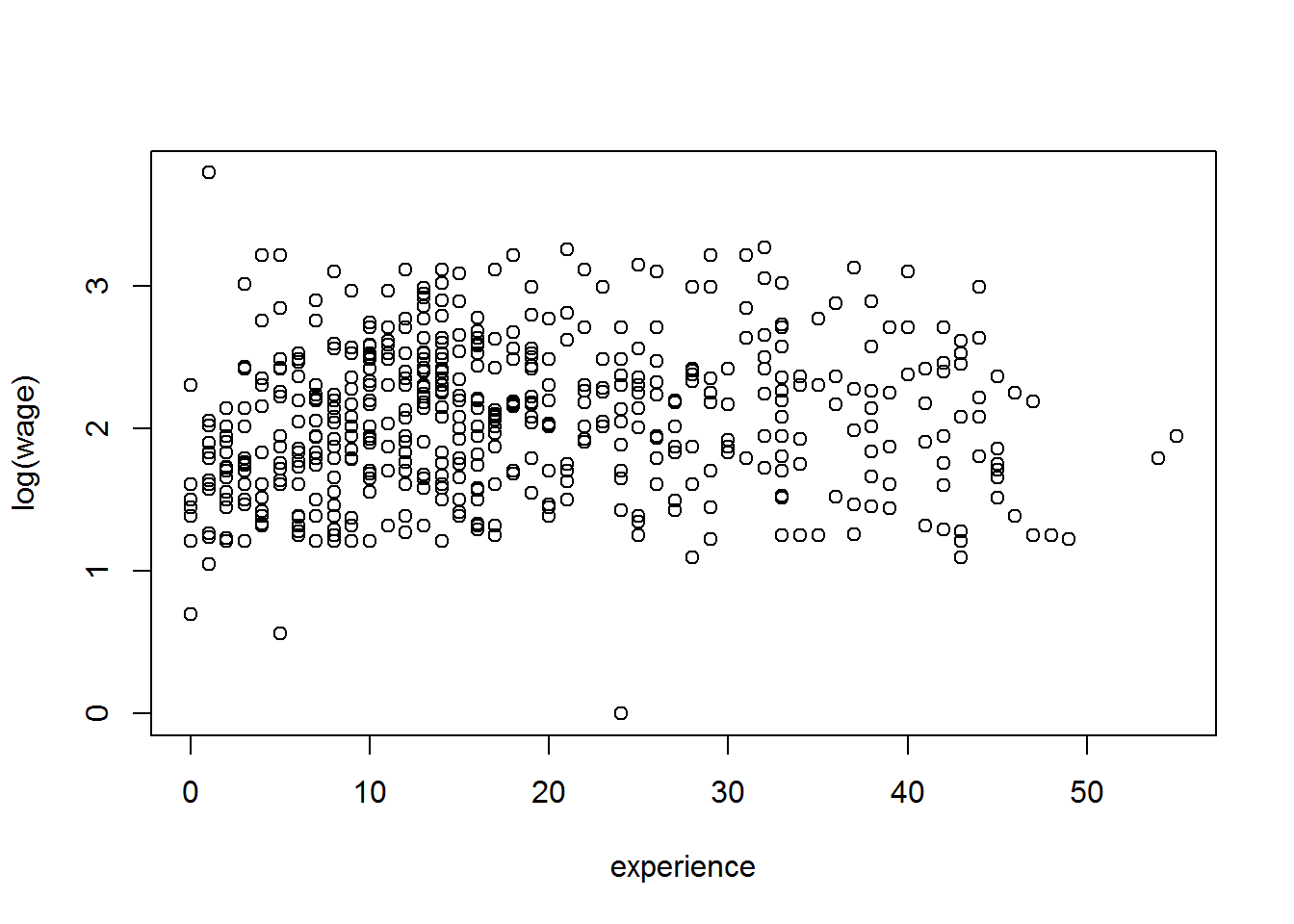
También lo podíamos haber escrito así:
plot (log(wage) ~ experience)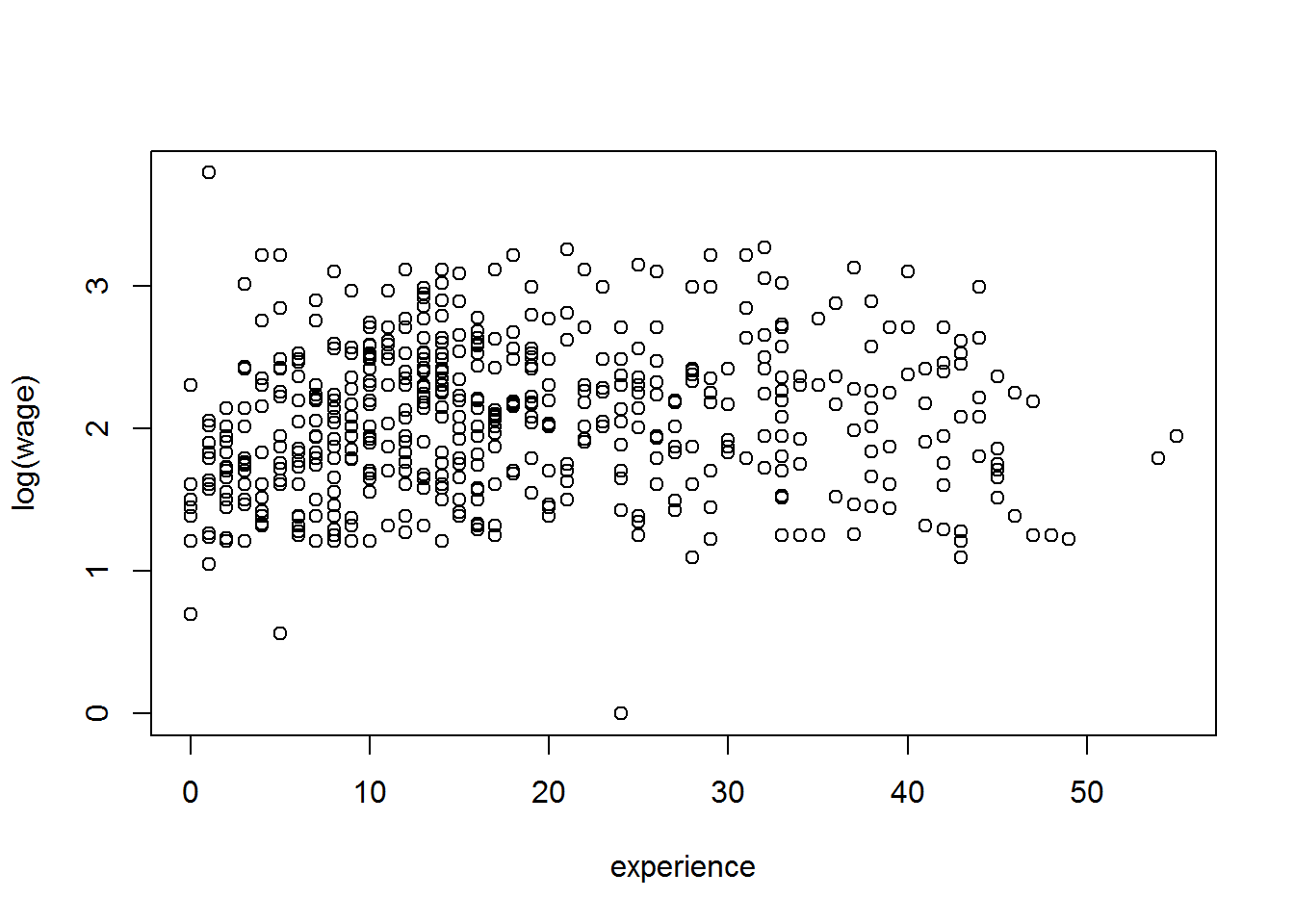
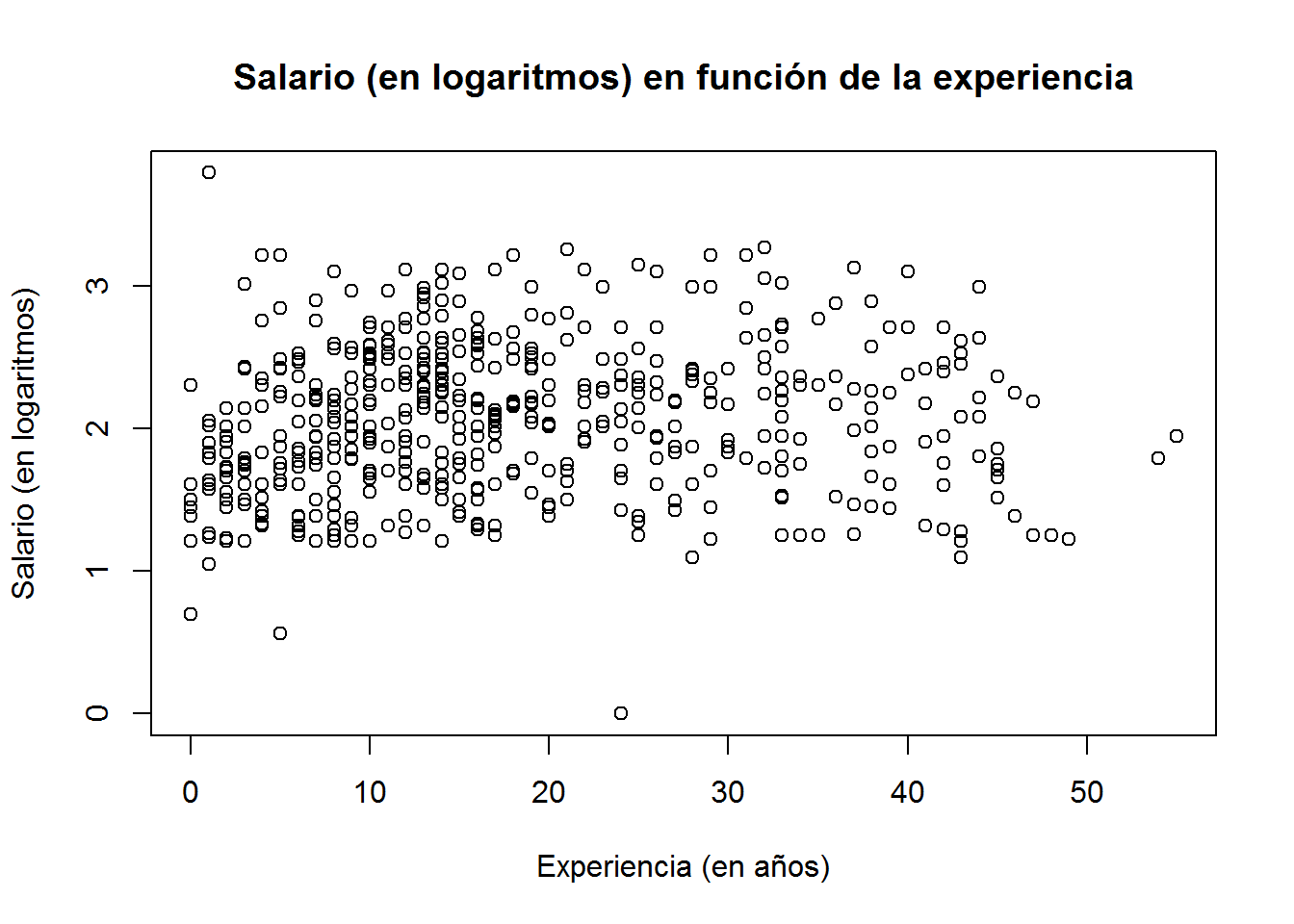
Como siempre, lo primero para mejorar la presentación de nuestro gráfico de dispersión será incluir el título del gráfico y de los ejes (también podemos incluir esta información utilizando la función title() (echad un vistazo a esta función, ?title).
plot (log(wage) ~ experience,
main = "Salario (en logaritmos) en función de la experiencia",
xlab = "Experiencia (en años)",
ylab = "Salario (en logaritmos)"
)
¿Queremos ver el salario en función de la experiencia y del género?
plot (log(wage) ~ experience,
col = rainbow(2)[c(gender)], # asigna color a los puntos en función del género
main = "Salario (en logaritmos) en función de la experiencia",
xlab = "Experiencia (en años)",
ylab = "Salario (en logaritmos)"
)
legend("topright", pch=16, col=rainbow(2), legend=c("Hombres","Mujeres")) # añadimos una leyenda al gráfico
Con la función abline() podemos añadir la recta de regresión en el diagrama de dispersión. Por ahora únicamente vamos a limitarnos a ver el efecto de la recta de regresión sobre el diagrama de dispersión. En otro curso estudiaremos, con cierta profundidad, los modelos de regresión con R.
# En primer lugar, obtenemos las regresiones
regresion_hombres <- lm(log(wage) ~ experience, data=CPS1985, subset=gender=="male")
regresion_mujeres <- lm(log(wage) ~ experience, data=CPS1985, subset=gender=="female")
plot (log(wage) ~ experience,
col = rainbow(2)[c(gender)], # asigna color a los puntos en función del género
main = "Salario (en logaritmos) en función de la experiencia",
xlab = "Experiencia (en años)",
ylab = "Salario (en logaritmos)"
)
legend("topright", pch=16, col=rainbow(2), legend=c("Hombres","Mujeres"))
abline(regresion_hombres, col="red")
abline(regresion_mujeres, col="blue")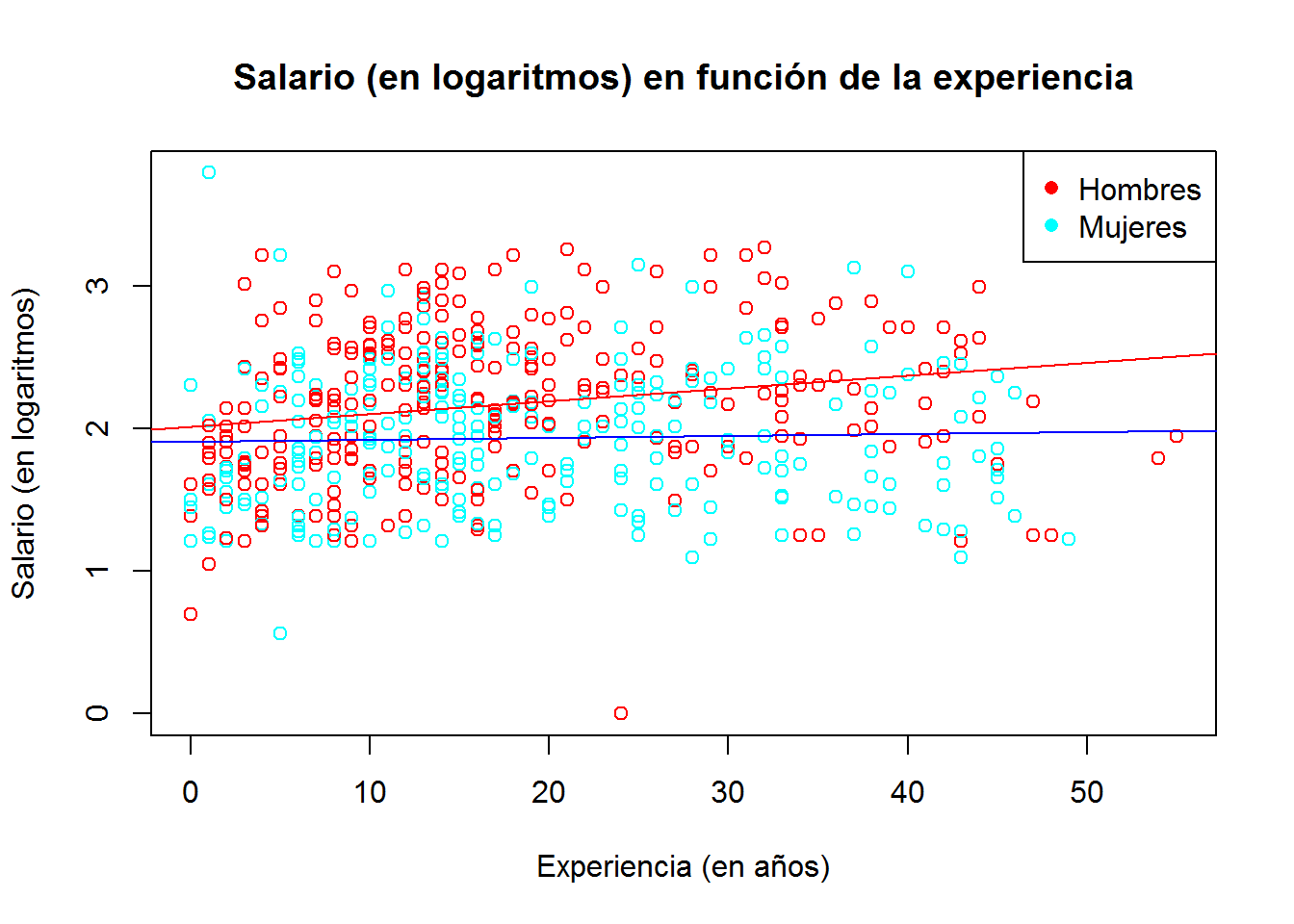
Un diagrama de dispersión alternativo al anterior.
sexo <- as.numeric(gender)
plot (log(wage) ~ experience,
pch = sexo,
col = sexo,
main = "Salario (en logaritmos) en función de la experiencia",
xlab = "Experiencia (en años)",
ylab = "Salario (en logaritmos)"
)
with(CPS1985[gender=="male",], abline(lm(log(wage)~experience), col="red"))
with(CPS1985[gender=="female",], abline(lm(log(wage)~experience), col="black"))
legend("topright", legend=c("Hombres","Mujeres"), pch=1:2, col=1:2, bty="y")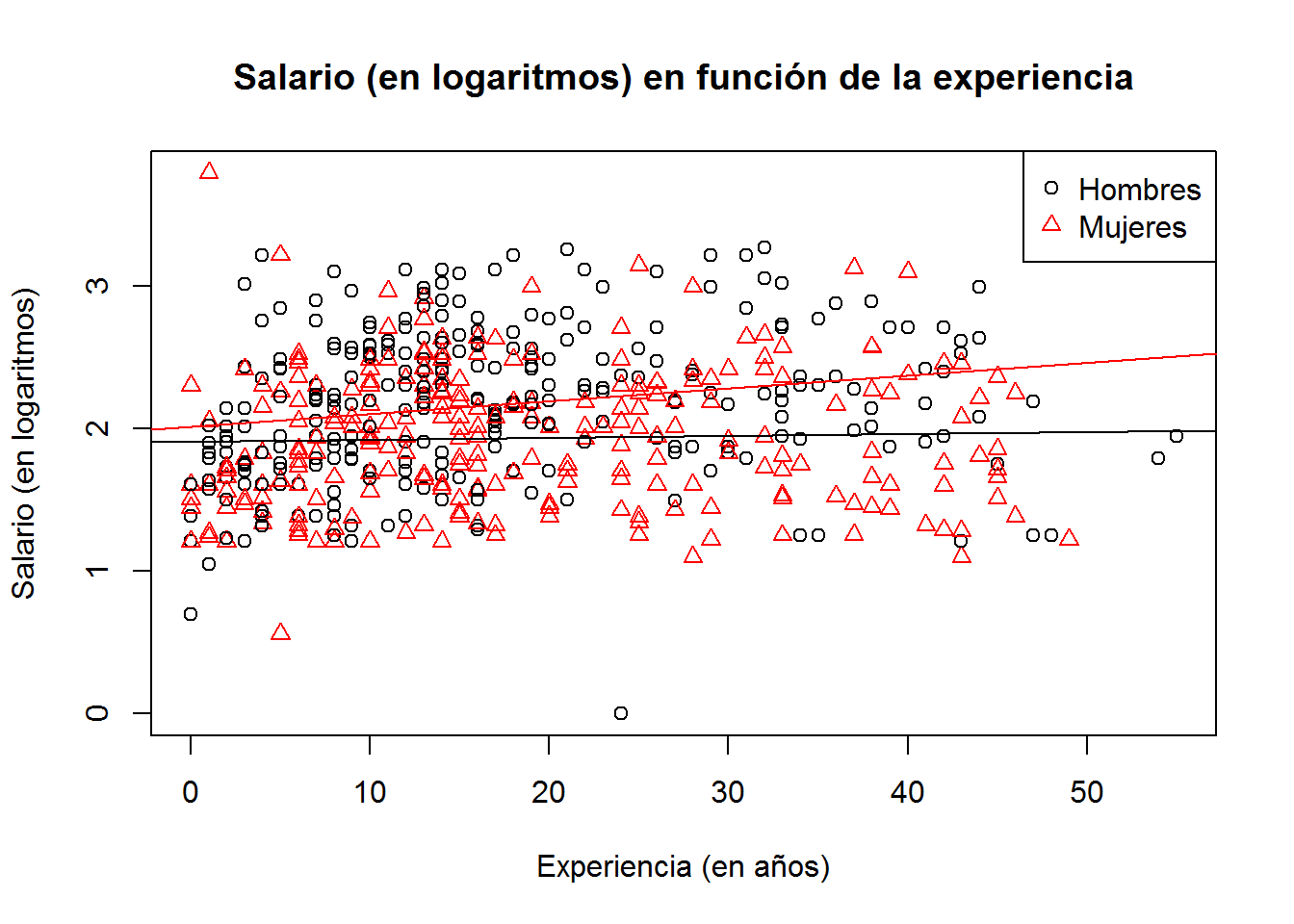
Para concluir, vamos a localizar el centro de gravedad (coordenadas correspondientes a las medias de las variables) en el gráfico de dispersión. Para ello usaremos la función points(). Como hay muchos puntos en el diagrama de dispersión, vamos a quitar los colores para poder ver donde cae el centro de gravedad.
sexo <- as.numeric(gender)
plot (log(wage) ~ experience,
pch = sexo,
main = "Salario (en logaritmos) en función de la experiencia",
xlab = "Experiencia (en años)",
ylab = "Salario (en logaritmos)"
)
with(CPS1985[gender=="male",], abline(lm(log(wage)~experience), col="black"))
with(CPS1985[gender=="female",], abline(lm(log(wage)~experience), col="black"))
legend("topright", legend=c("Hombres","Mujeres"), pch=1:2, bty="y")
points(mean(experience), mean(log(wage)), pch=16, col="red")
y utilizando la función abline() podemos dibujar las rectas que pasan representar las líneas (quitamos las rectas de regresión para poder ver con mayor claridad el efecto).
sexo <- as.numeric(gender)
plot (log(wage) ~ experience,
pch = sexo,
main = "Salario (en logaritmos) en función de la experiencia",
xlab = "Experiencia (en años)",
ylab = "Salario (en logaritmos)"
)
legend("topright", legend=c("Hombres","Mujeres"), pch=1:2, bty="y")
points(mean(experience), mean(log(wage)), pch=16, col="red")
abline(v=mean(experience), h=mean(log(wage)))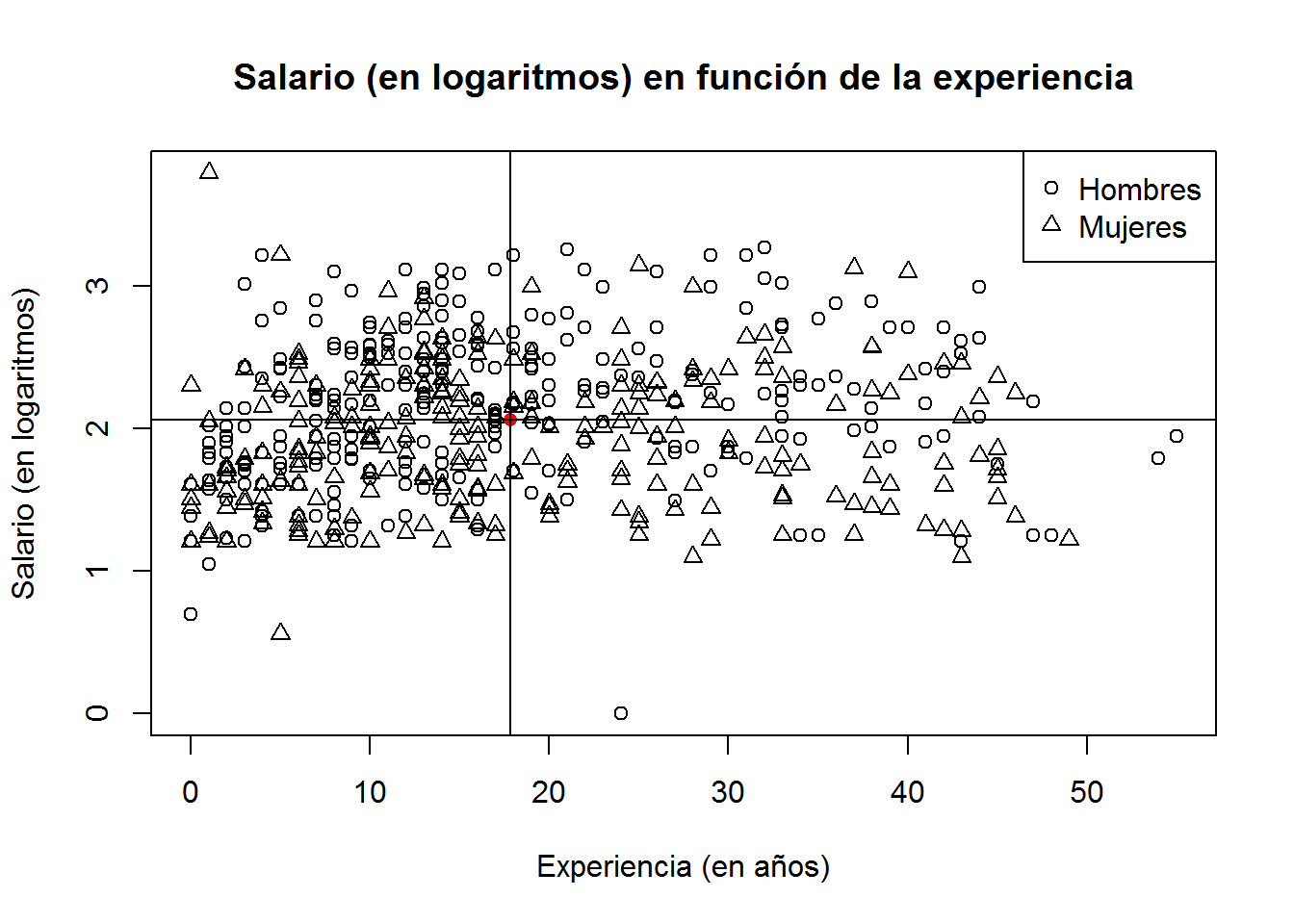
- Tarea. Realizar un diagrama de dispersión para analizar la posible relación entre el salario (en logaritmos) y la edad (age) distinguiendo según la raza (ethnicity).
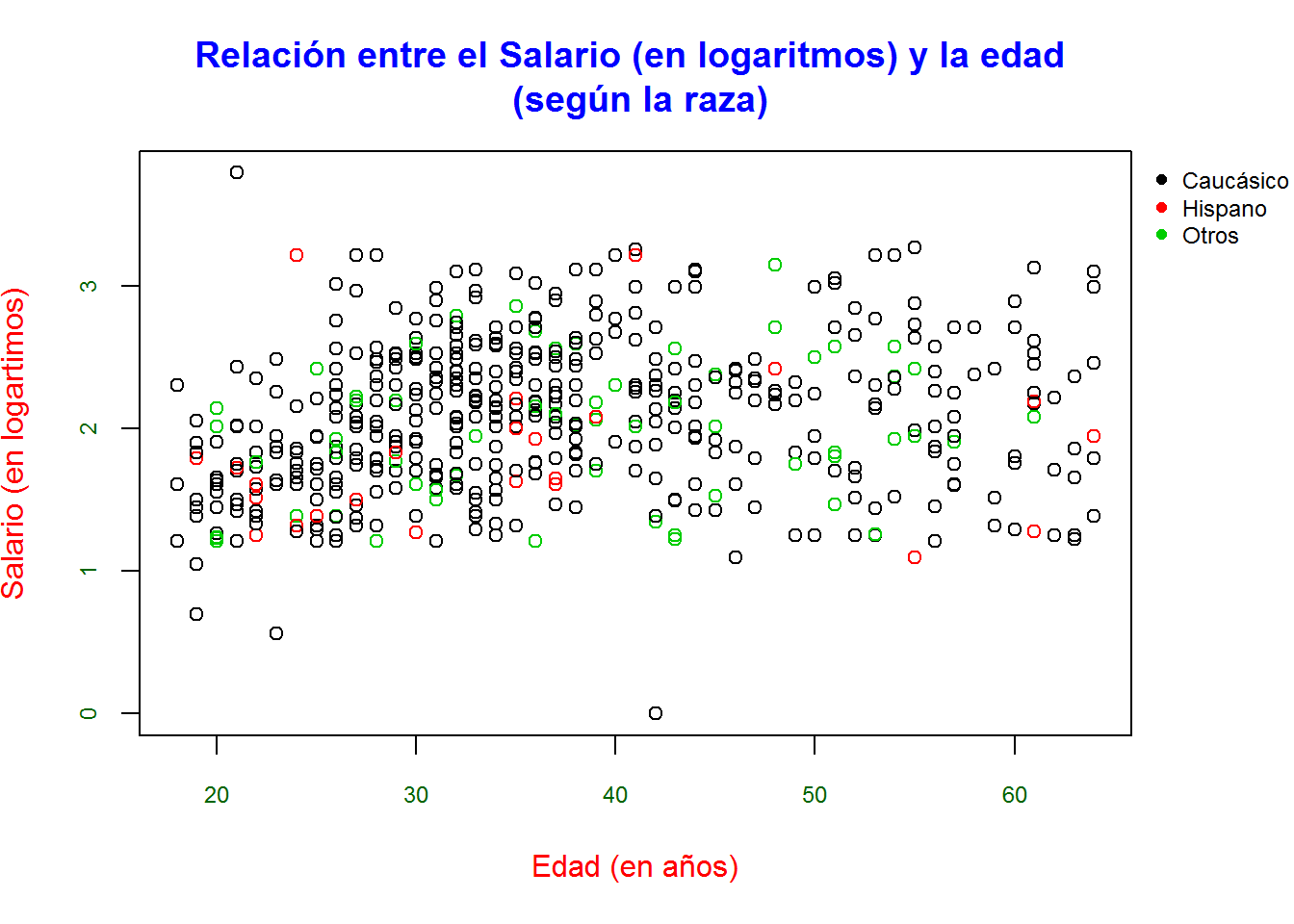
Diagrama de barras.
Para realizar un diagrama de barras primero tenemos que obtener la tabla de las frecuencias y después la representamos utilizando la función barplot().
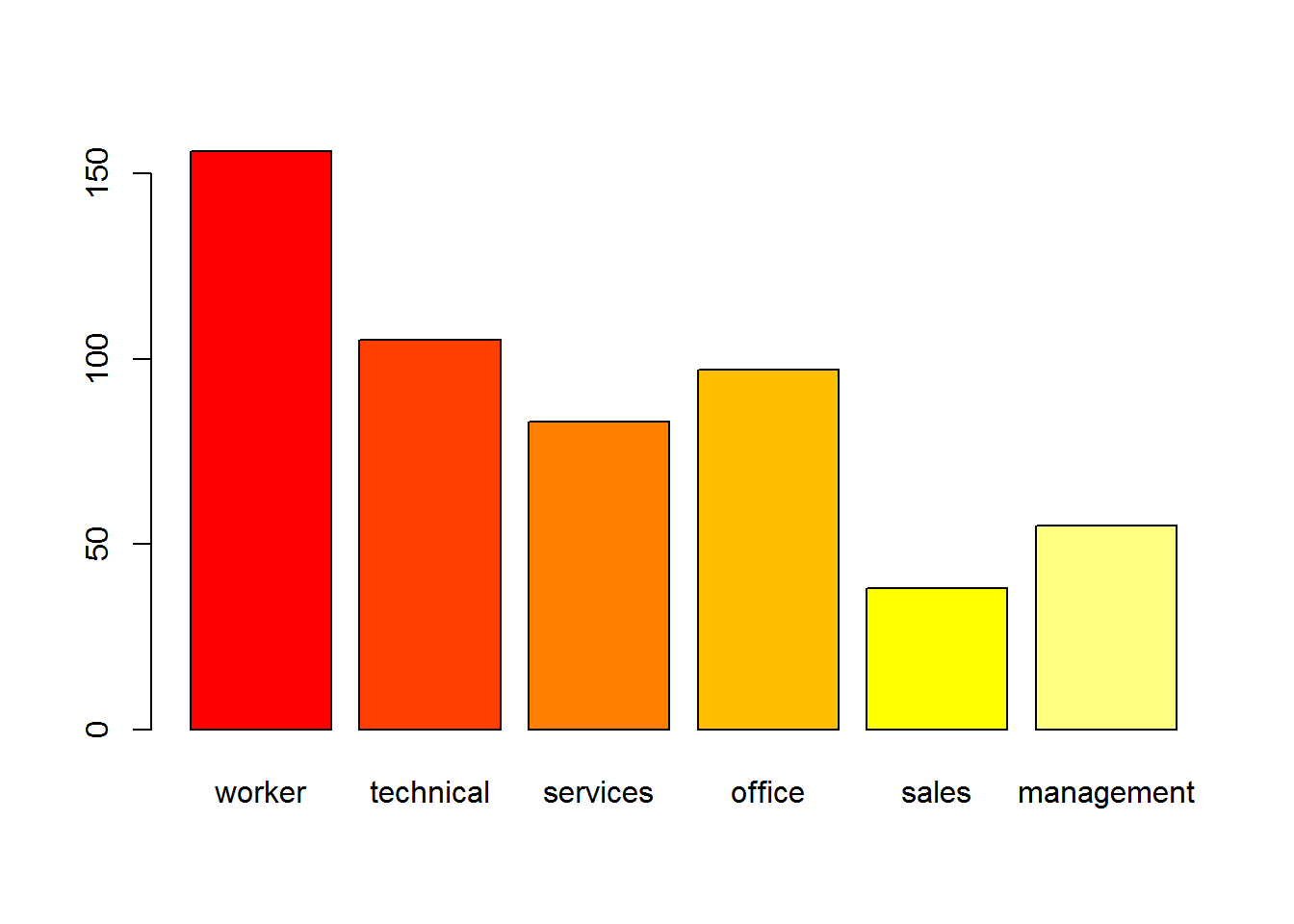
Comenzamos realizando un diagrama de barras para ver la distribución de la variable Ocupación (Occupation).
frecuencias <- table(occupation) # con variable categórica
frecuencias
## occupation
## worker technical services office sales management
## 156 105 83 97 38 55
barplot(frecuencias,
col = heat.colors(6)
)
Vamos a hacer un diagrama de barras con una variable discreta, por ejemplo: educación (education).
educacion <- table(education)
p <- barplot(educacion,
col = 1:dim(educacion), # para establecer el número de diferentes colores (=diferentes valores)
space = 0, # no espacio entre las barras
horiz = F, # orientación de las barras
density = 50 , # trama de las barras (se puede modificar el ángulo con el argumento angle)
ylim = c(0,250)
)
title("Distribución de la edad", xlab= "Edad (en años)")
text(p[,1],educacion,labels=educacion, pos=3,cex=0.75)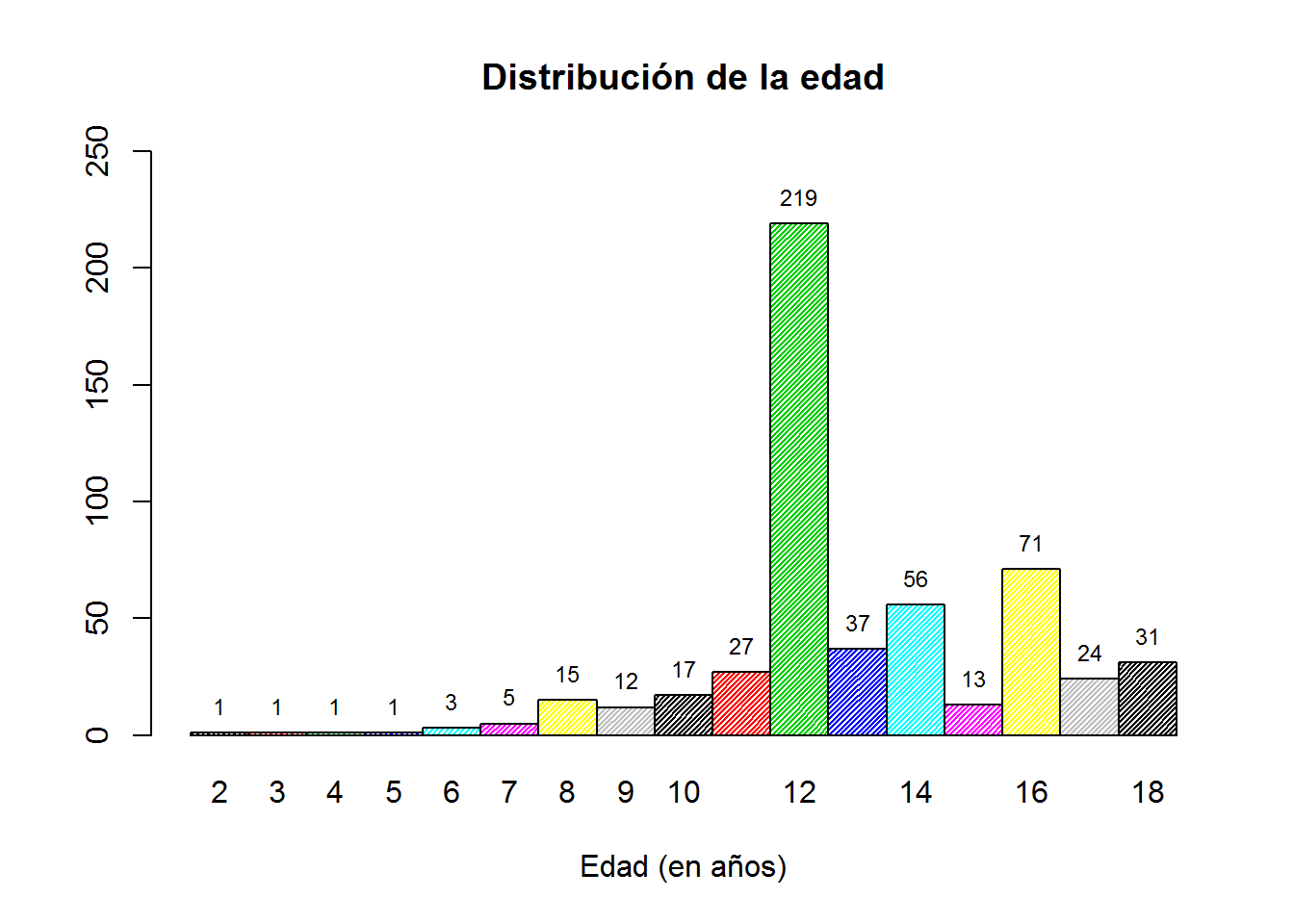
Para ver cómo se distribuye una variable categórica según, generalmente, las categorías de una segunda variable suele utilizarse un diagrama de barras apiladas.
g <- table(ethnicity, gender)
barplot(g,
beside = F, # para apilar las barras
col = rainbow(3),
ylim = c(0,350)
)
# Add text at top of bars
legend("topright", title="Raza", legend=levels(ethnicity), fill=rainbow(3), cex=.75, border=F, horiz=T, text.col="purple")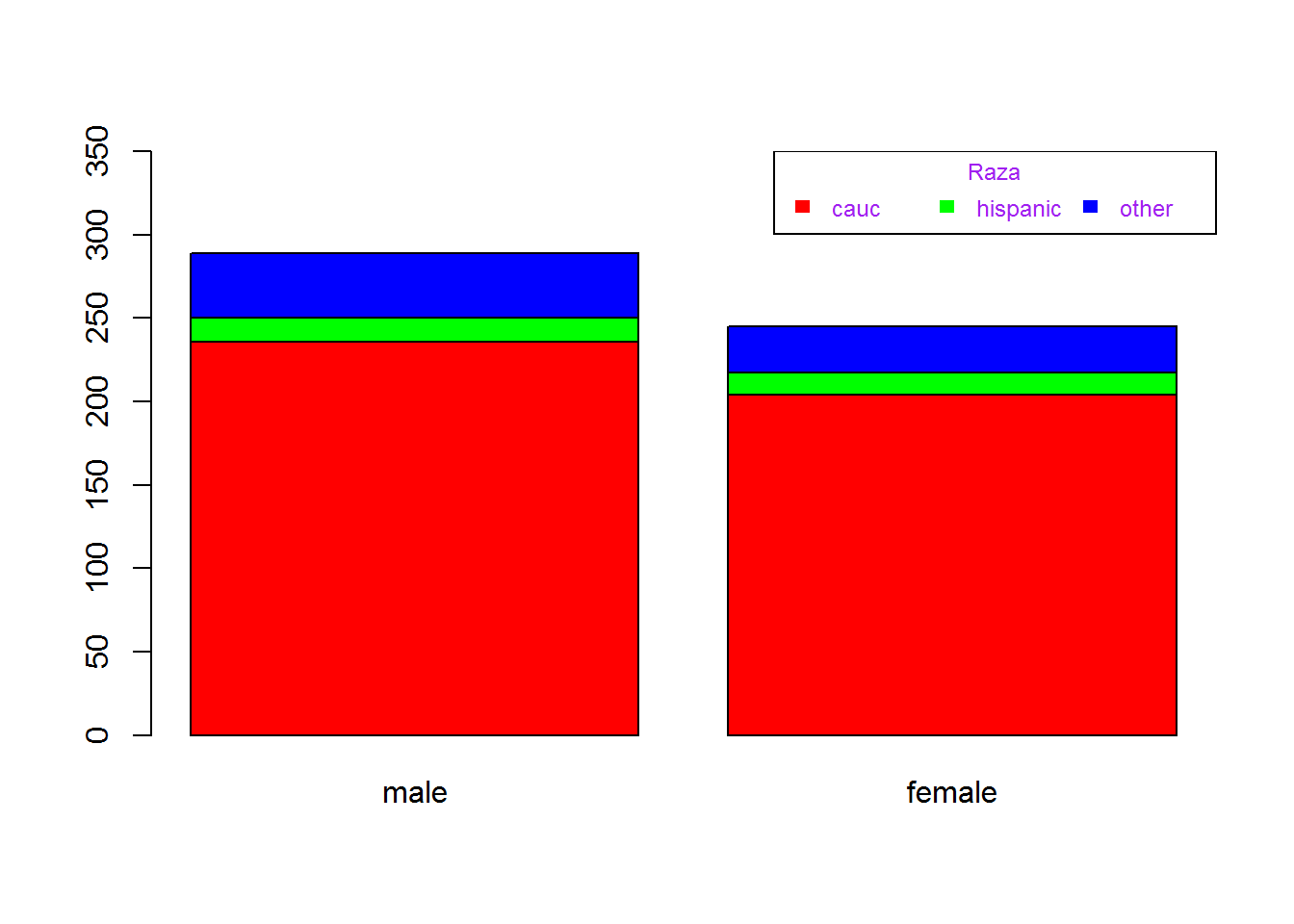
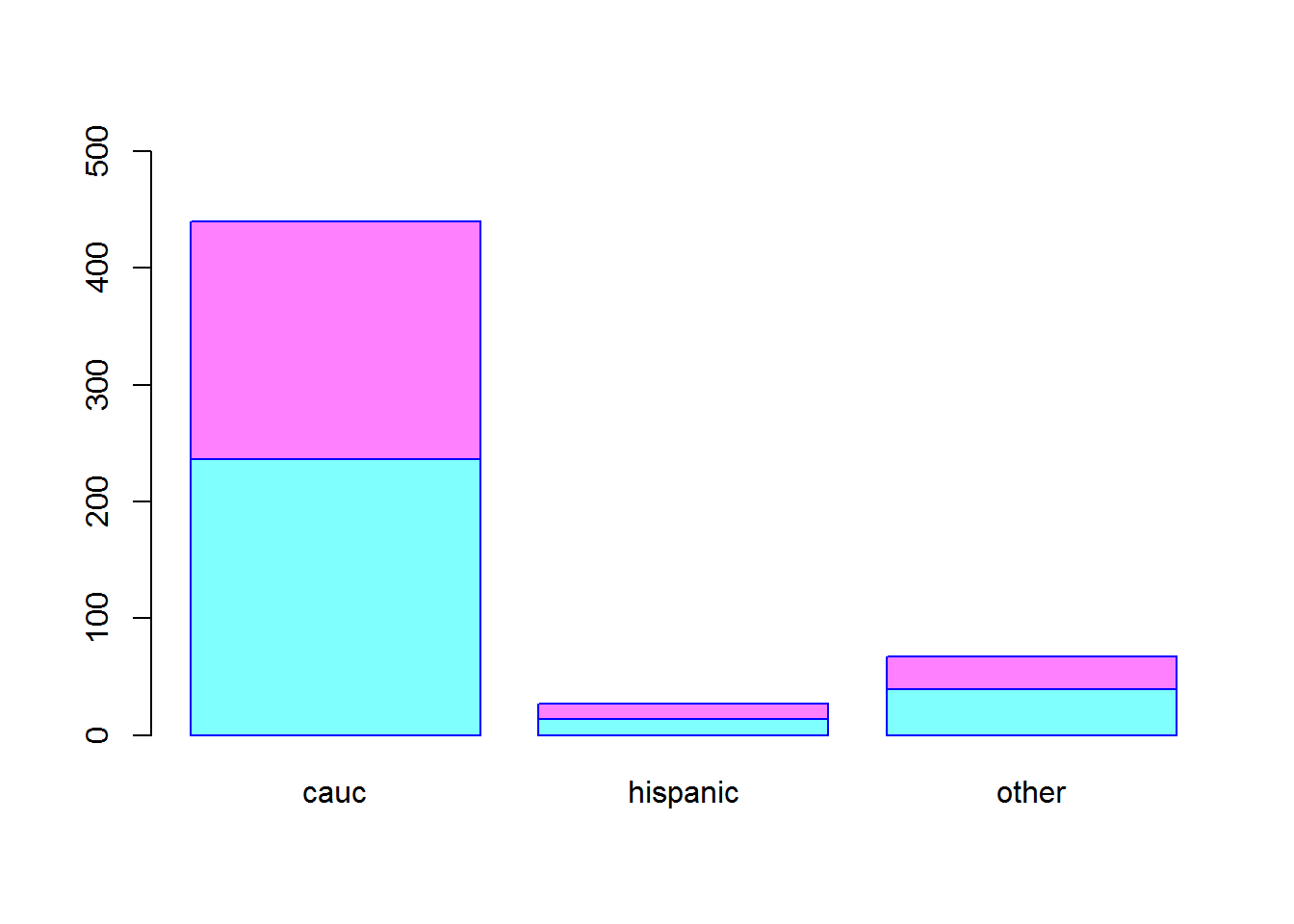
Observemos la diferencia del anterior gráfico respecto de este otro.
e <- table(gender, ethnicity)
barplot(e,
beside = F,
col = cm.colors(2),
ylim = c(0,500),
border = "blue"
)
p <- table(ethnicity, gender)
barplot(p,
beside=T, # si es FALSE apila
col=rainbow(3),
legend=levels(ethnicity),
names.arg= levels(gender),
ylim=c(0,250)
)
Para dibujar diagramas de barras también se puede utilizar la función plot(). Aquí hay algún ejemplo:
plot(frecuencias, type=“h”)
plot(density(log(wage)))
plot (gender ~ occupation)
Otros gráficos básicos.
Gráficos de sectores
datos <- table(ethnicity)
pie(datos,
labels=c("Caucásicos", "Hispanos", "Otros"),
col=heat.colors(3),
main= "Gráfico de sectores")
Gráfico de mosaico
mosaicplot(ethnicity ~ occupation,
col=2:5,
main="Gráfico de mosaico",
xlab="Raza",
ylab="Ocupación",
cex.axis=.5,
las=1)
#install.packages("vcd")
library(vcd)
datos <- ftable(occupation, ethnicity, gender)
mosaic(~ occupation + ethnicity + gender , dat=datos, las=1)
3. Guardar y exportar gráficos
Si trabajamos con la interfaz de R que proporciona RStudio y queremos guardar o exportar un gráfico normalmente hacemos lo siguiente:
Ejecutamos el script del gráfico que queremos guardar. Este gráfico aparecerá en la pestaña Plots del entorno de trabajo de RStudio.
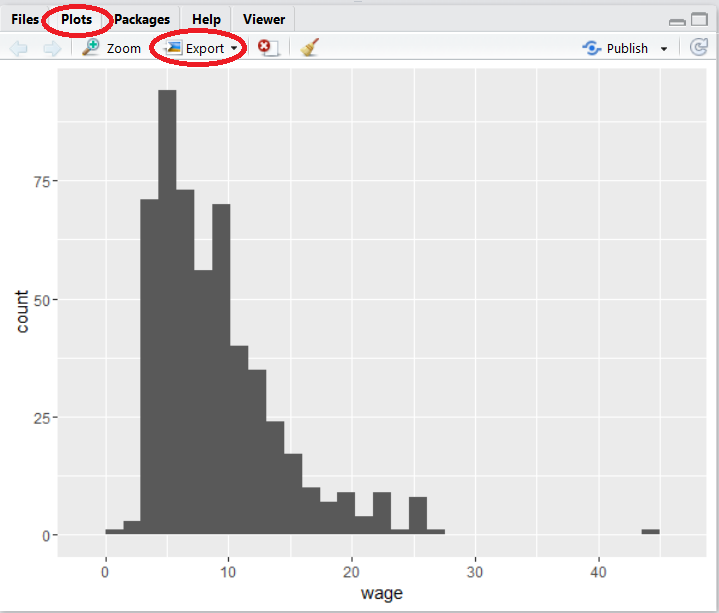
Guardar gráfico en R
Al seleccionar la opción Export se desplegará una lista con tres opciones:
- Guardar como imagen (Save as image…). El formato de salida del gráfico puede ser: “.png”, “.jpeg”, “.tiff”, “.bmp”, etc. También podemos cambiar las dimensiones (anchura y altura) del gráfico. Si vamos a utilizar el gráfico en Word es conveniente guardar el gráfico como Metafile.
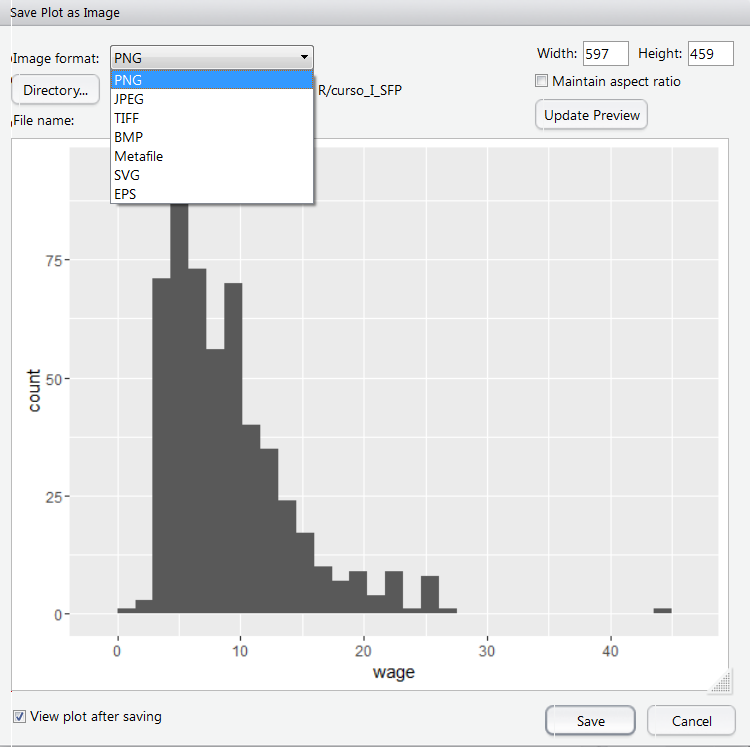
Opciones de salida para guardar gráfico
Guardar como pdf (Save as pdf…).
Copiar al portapapeles (Copy to clipboard…)
Existen otras opciones para guardar los gráficos. Aquí os dejamos un enlace a un vídeo en youtube titulado Exportar gráficos del blog R para principiantes, y este otro enlace al blog Picando con R tenéis un post donde se explica de forma muy sencilla cómo guardar los gráficos como archivo de imagen.
4. ggplot2.
Una vez nos hemos familiarizado con la creación de gráficos (básicos) utilizando R base, en este apartado vamos a reproducir los gráficos que hemos ido trabajando pero haciendo uso de ggplot2. Creo que no nos equivocamos si decimos que, hoy en día, las representaciones gráficas en R pasan por ggplot2. Esta es la Cheat Sheet de RStudio con la ayuda para la visualización de datos con ggplot2.
Recordad que el manual “ggplot2. Elegant graphics for data analysis” de Wickham lo podéis descargar en este enlace si estáis en la red de la Universitat. También hay una lista de ggplot (http://ggplot2.org/) a la que os podéis subscribir. En palabras de Wickham “The list (…) is very friendly to new users”.
Un gráfico realizado con ggplot2 presenta, al menos, tres elementos:
- Datos (Data) que queremos representar (que serán un data frame).
- Características estéticas (aesthetic mappings) que describen cómo queremos que los datos se vean en el gráfico. Para más información podemos consultar la vignette (vignette(“ggplot2-specs”)). Como luego veremos, se introducen con la función aes() y se refieren a:
- posición (en los ejes)
- color exterior (color) y de relleno (fill)
- forma de puntos (shape)
- tipo de línea (linetype)
- tamaño (size)
- Objetos geométricos (Geom) representan lo que vemos en un gráficos (puntos, líneas, etc.). Todo gráfico tiene, como mínimo, una geometría. La geometría determina el tipo de gráfico:
- geom_point (para puntos)
- geom_lines (para lineas)
- geom_histogram (para histograma)
- geom_boxplot (para boxplot)
- geom_bar (para barras)
- geom_smooth (líneas suavizadas)
- geom_polygons (para polígonos en un mapa)
- etc. (si ejecutáis el comando help.search(“geom_”, package = “ggplot2”) podéis ver el listado de objetos geométricos)
Por tanto, para construir un gráfico con ggplot2 comenzamos con la siguiente estructura de código:
ggplot(datos, aes()) + geom_tipo()
A partir de esta estructura básica puede mejorarse la presentación de los gráficos introduciendo, por ejemplo, características estéticas en los objetos geométricos, rotulando el gráficos, etc.
Otros elementos que conviene tener presente en un gráfico de ggplot2 son:
- Stat (Stat), transformaciones estadísticas para, generalmente, resumir datos (por ejemplo: contar frecuencias, número de intervalos en los histogramas, etc.).
- Escalas (Scale). Las escalas, por ejemplo, convierten datos en características estéticas (colores, etc.), crean leyendas… . - Coordenadas (coord): sistema de coordenadas cartesianas, polares, proyecciones, etc.
- Faceting (Faceting), permite representar gráficos separados para subconjuntos de los datos originales.
Vamos a realizar algunos gráficos con ggplot. Para ello, cargamos la librería ggplot2. Si no está instalado el paquete lo instalamos.
#install.packages("ggplot2")
library(ggplot2)En los ejemplos que siguen tratamos de ir introduciendo poco a poco distintos elementos y argumentos para mejorar la apariencia de los gráficos.
Histogramas
Vamos a comenzar haciendo un histograma muy sencillo del Salario (wage). Para ello, recordemos que la instrucción comienza con la función ggplot(), en la que incluimos los datos y la estética con la que queremos que se presenten en el gráfico. Seguidamente le añadimos (+) la geometría (tipo histograma) con la función geom_histogram().
Muy importante: con ggplot2 añadimos capas (layers) con el símbolo +.
El histograma del Salario será:
ggplot(CPS1985, aes(x=wage)) +
geom_histogram()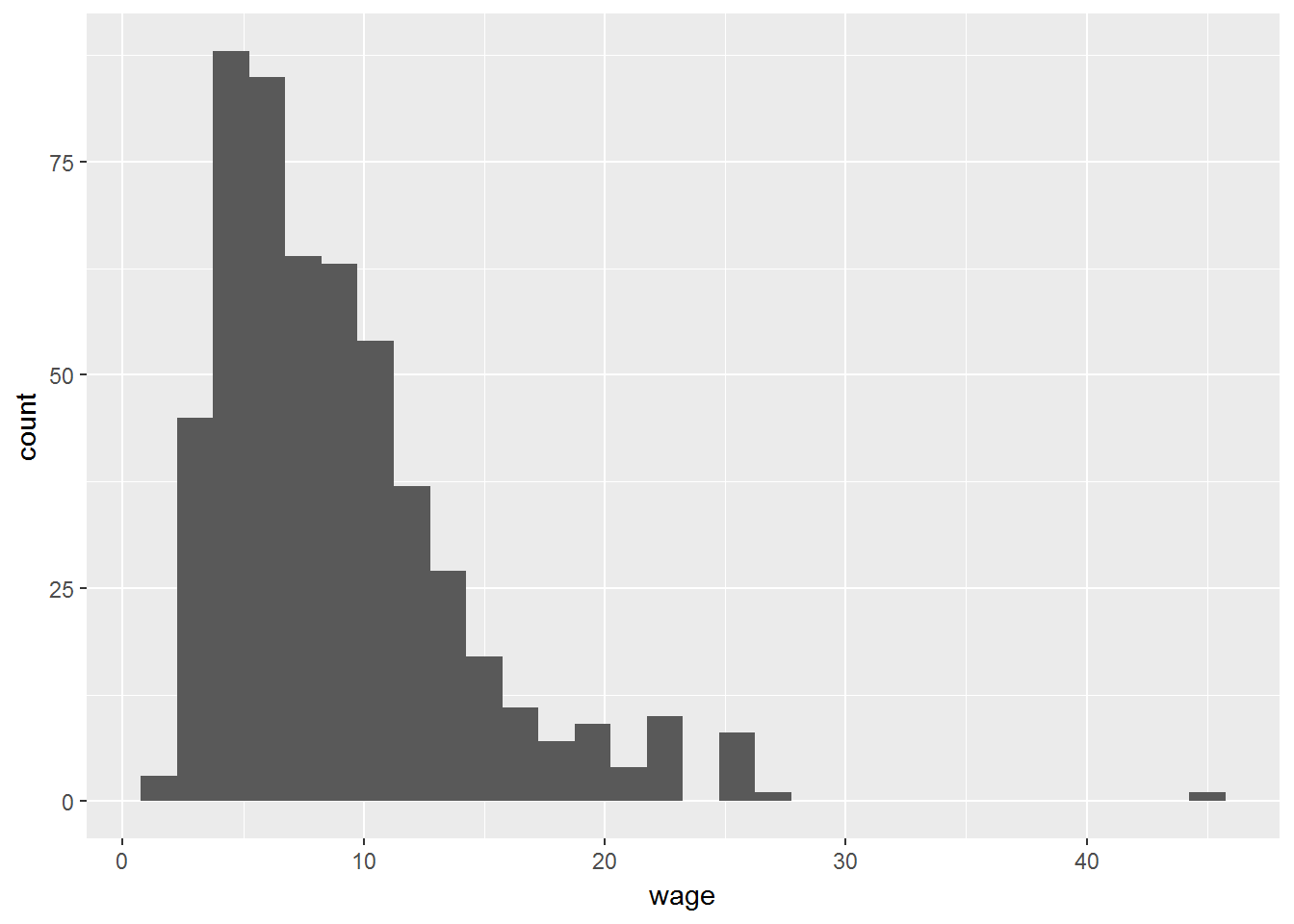
Dos cosas a considerar del histograma anterior:
- Por defecto, el número de intervalos es de 30. Es posible establecer el número de intervalos (bins), la amplitud del intervalo (binwidth) o fijar los puntos de corte de los intervalos (breaks).
- El eje Y corresponde al número de observaciones (frecuencias absolutas). Si estamos interesados en representar un histogramas de forma que el área del mismo sume 1, entonces tenemos que cambiar la estética de la siguiente forma:
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(aes(y=..density..))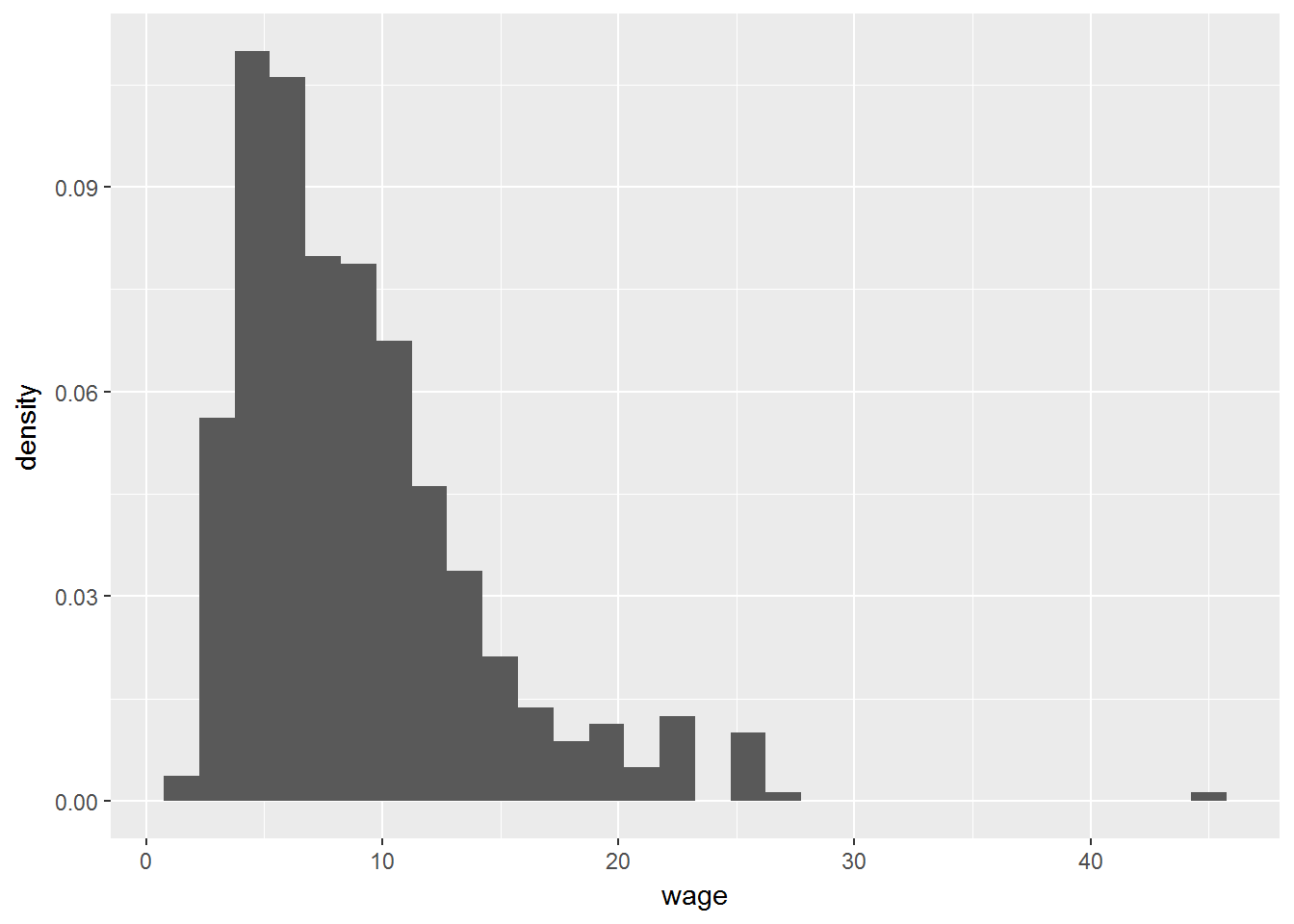
A partir de esta estructura básica, podemos ir añadiendo elementos para mejorar la presentación. Observad la diferencia entre los siguientes dos histogramas.
# Histograma con 20 intervalos
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(bins=20, color="white", fill="blue")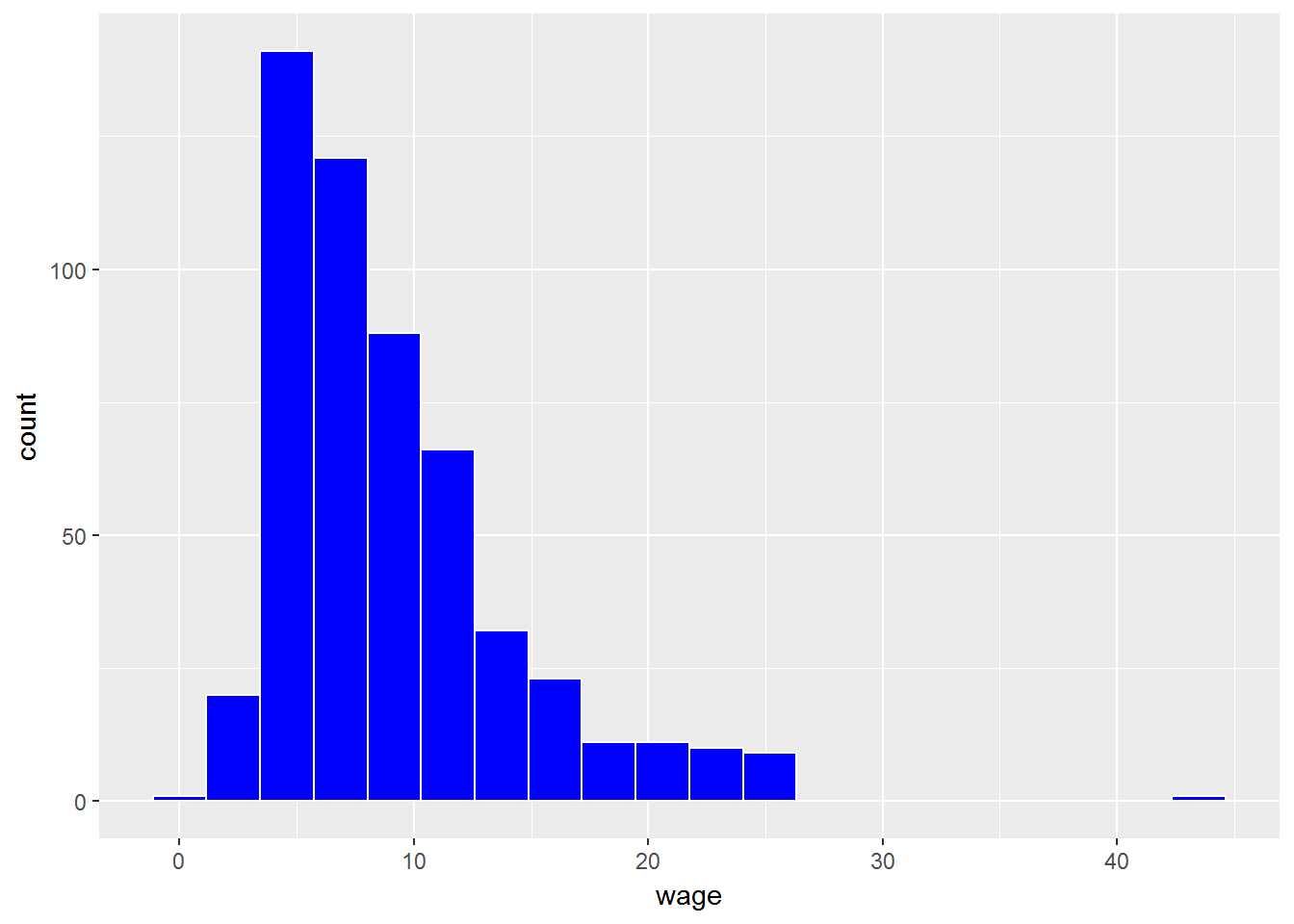
# Histograma con amplitud de intervalo igual a 5. Línea discontinua para el contorno del intervalo
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(binwidth=5, color="white", fill="blue", linetype=2)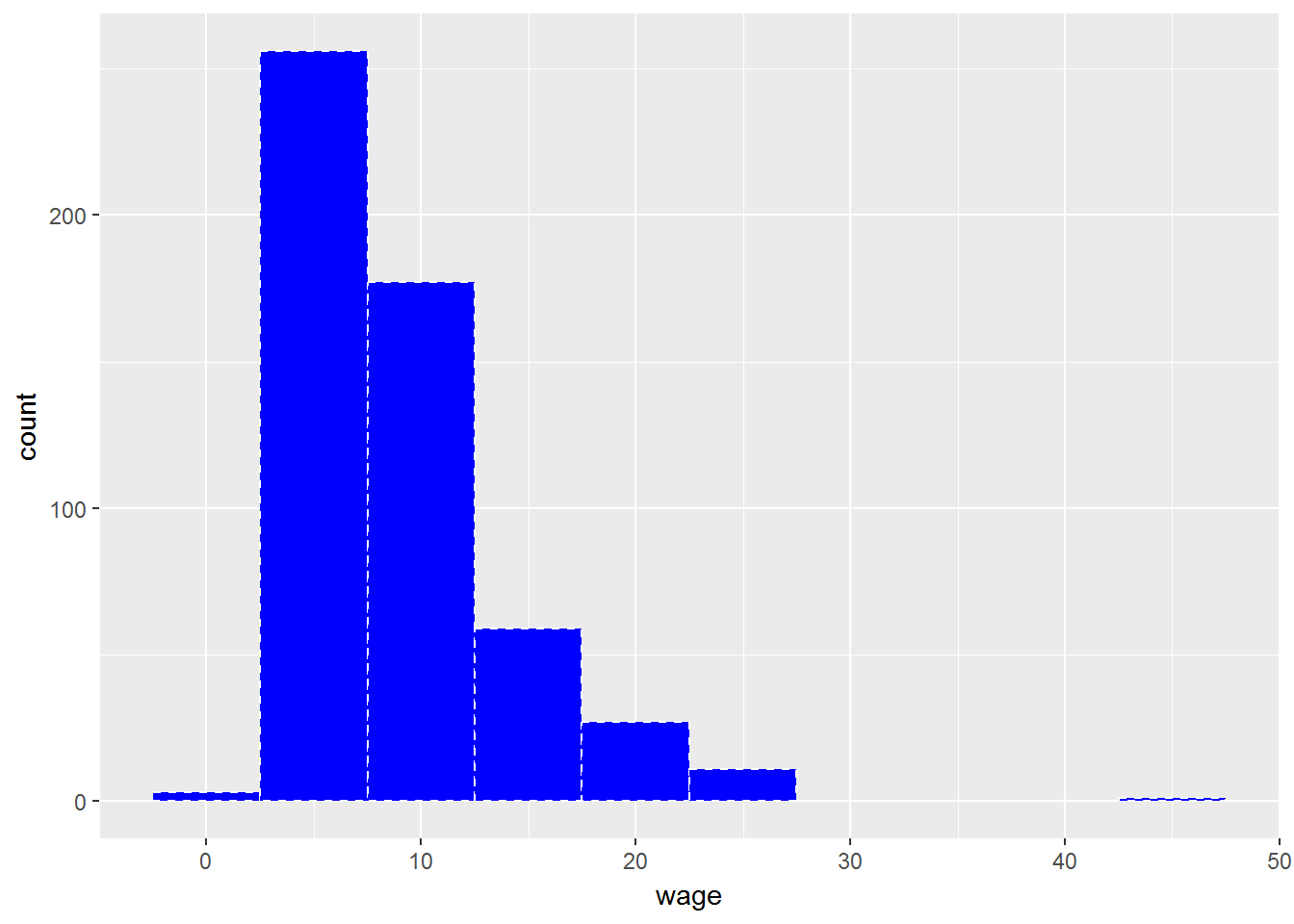
Ahora vamos a insertar un título al gráfico y también rotularemos los ejes. Para modificar las etiquetas de los ejes se utilizan las funciones xlab() y ylab(). Si, por ejemplo, quisiéramos omitir la etiqueta del eje Y: ylab(NULL).
También podemos cambiar los límites de los ejes, para ello se emplean las funciones xlim() y ylim().
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(bins=20, color="white", fill="blue") +
ggtitle("Distribución del salario (dólares por hora)") +
xlab("Salario") +
ylab("Número de empleados")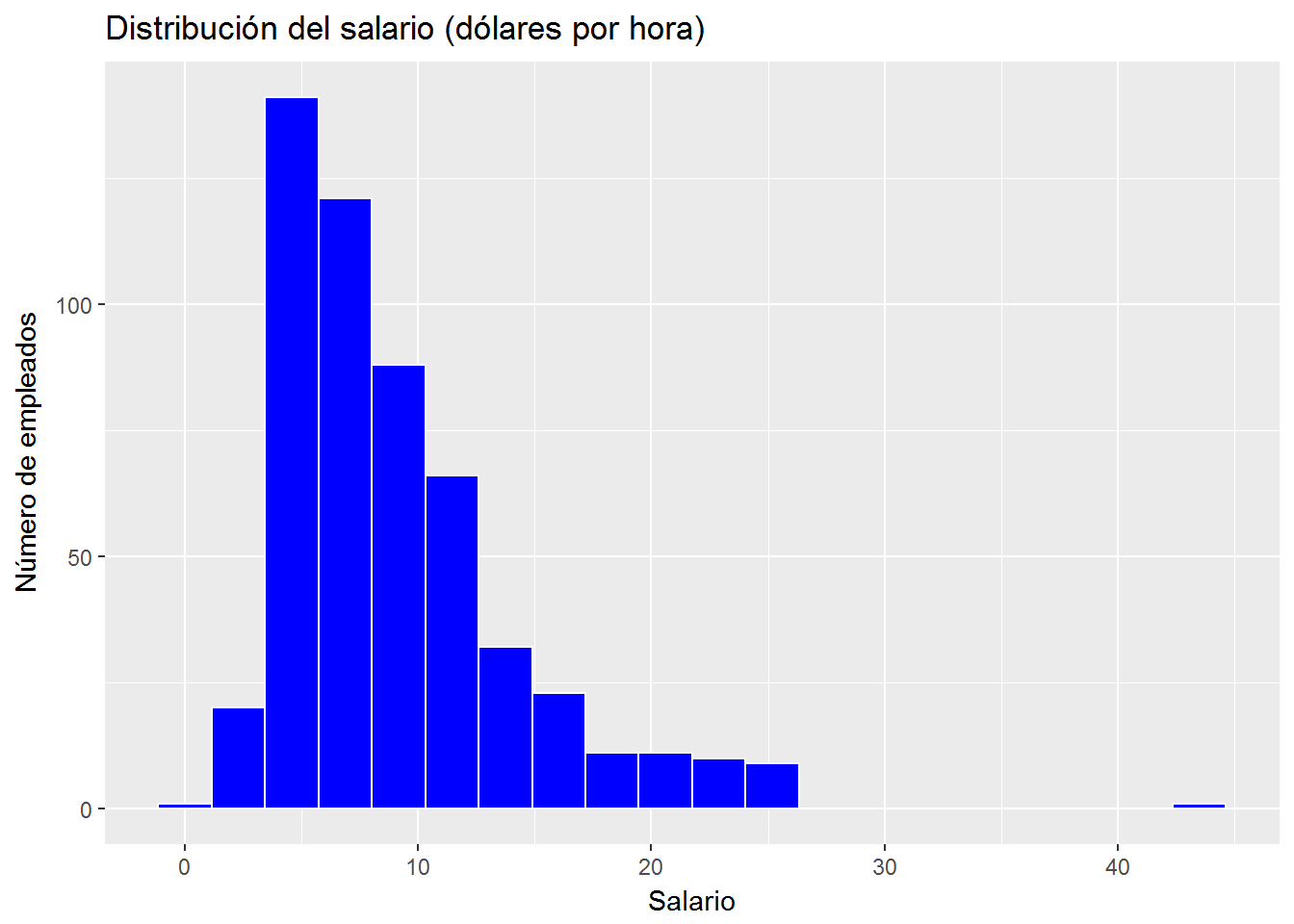
# Una alternativa al anterior sería:
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(bins=20, color="white", fill="blue") +
labs(title = "Distribución del salario (dólares por hora)",
x = "Salario",
y = "Número de empleados") +
ylim(c(0,150))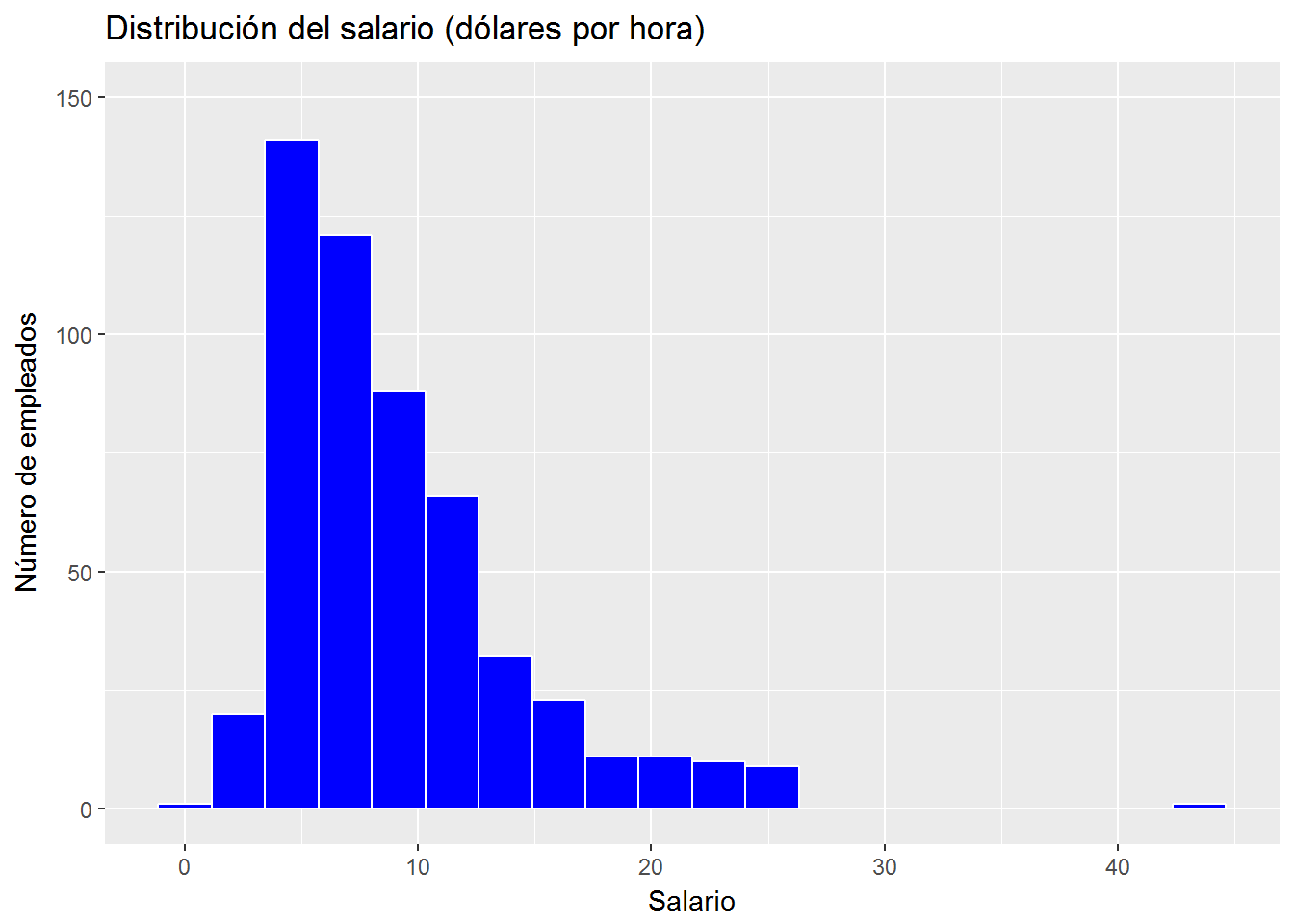
Para tratar de observar las diferencias en la distribución del salario según distintos grupo, por ejemplo, el género podemos:
- Visualizar cada subconjunto de datos (salario para hombres y salario para mujeres) en distintos paneles. Para ello, utilizamos el elemento facet.
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(bins=20, color="white", fill="blue") +
facet_grid(gender~.)
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(bins=20, color="white", fill="blue") +
facet_wrap(~gender)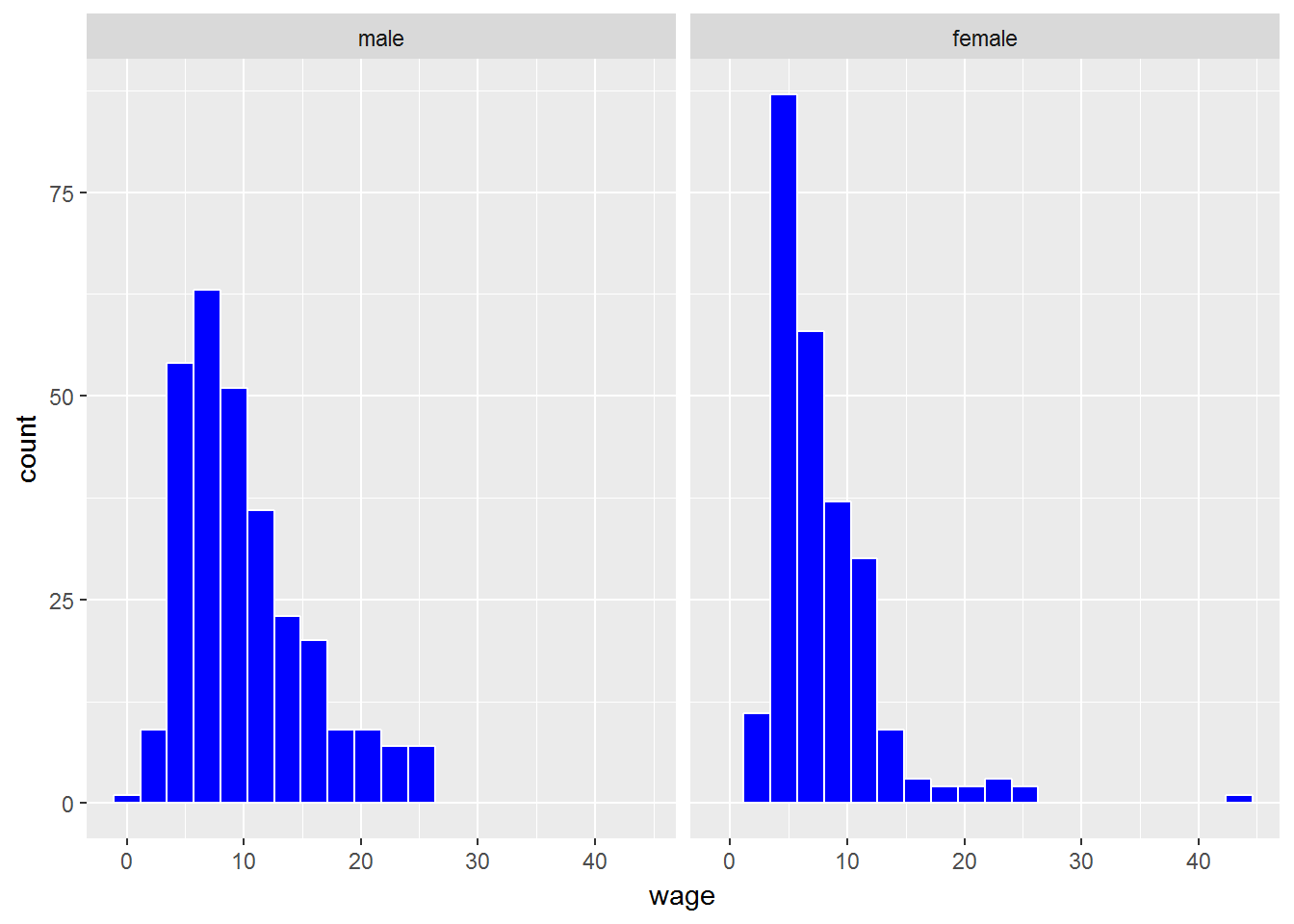
- Hacemos el histograma pero usamos el género para colorear las partes que de cada intervalo corresponden a hombres y a mujeres. Fijémonos en los siguientes tres histogramas.
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(bins=20, aes(color=gender) ) +
ylim(c(0,150))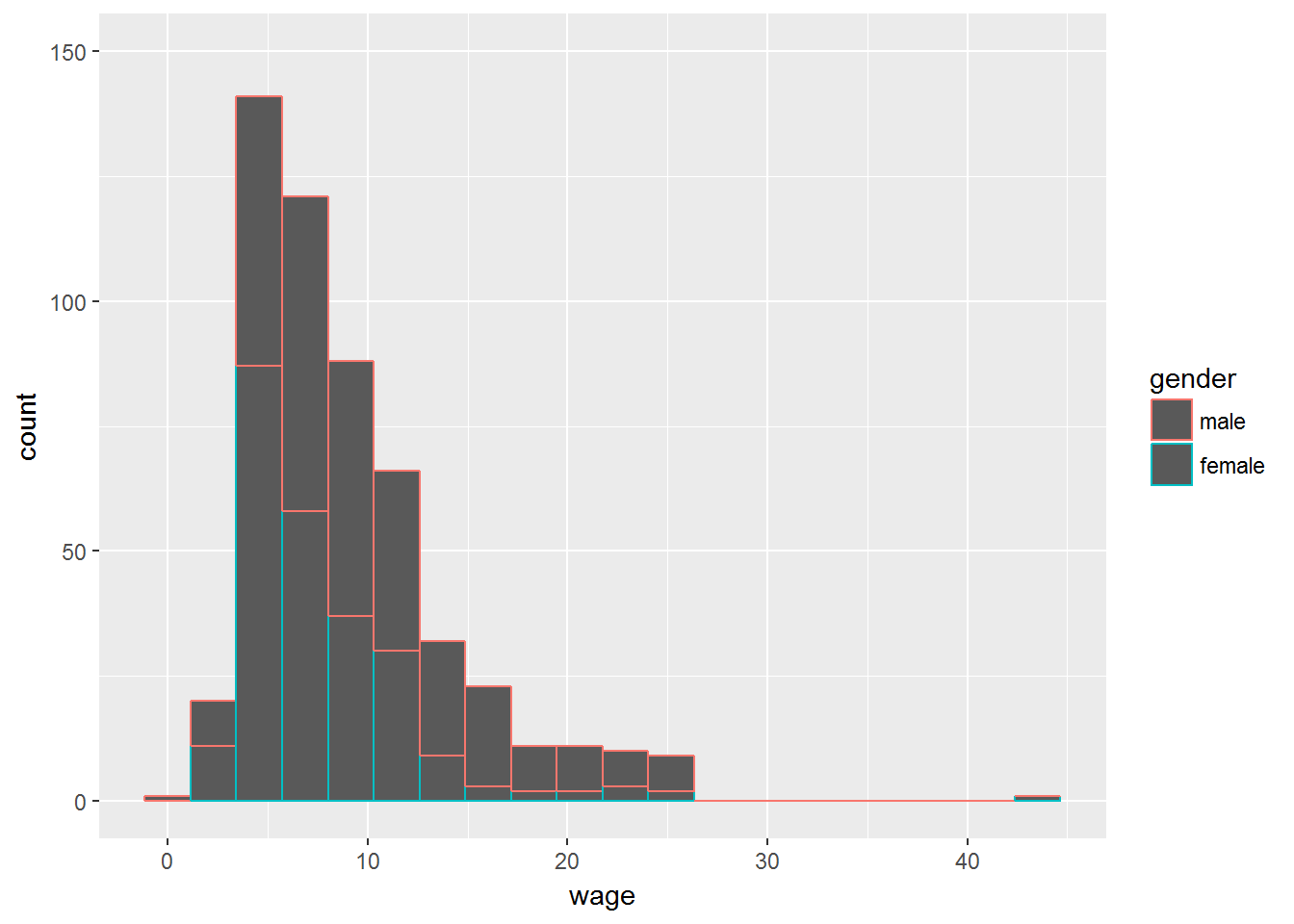
ggplot(CPS1985, aes(x=wage, fill=gender)) +
geom_histogram(bins=20) +
ylim(c(0,150))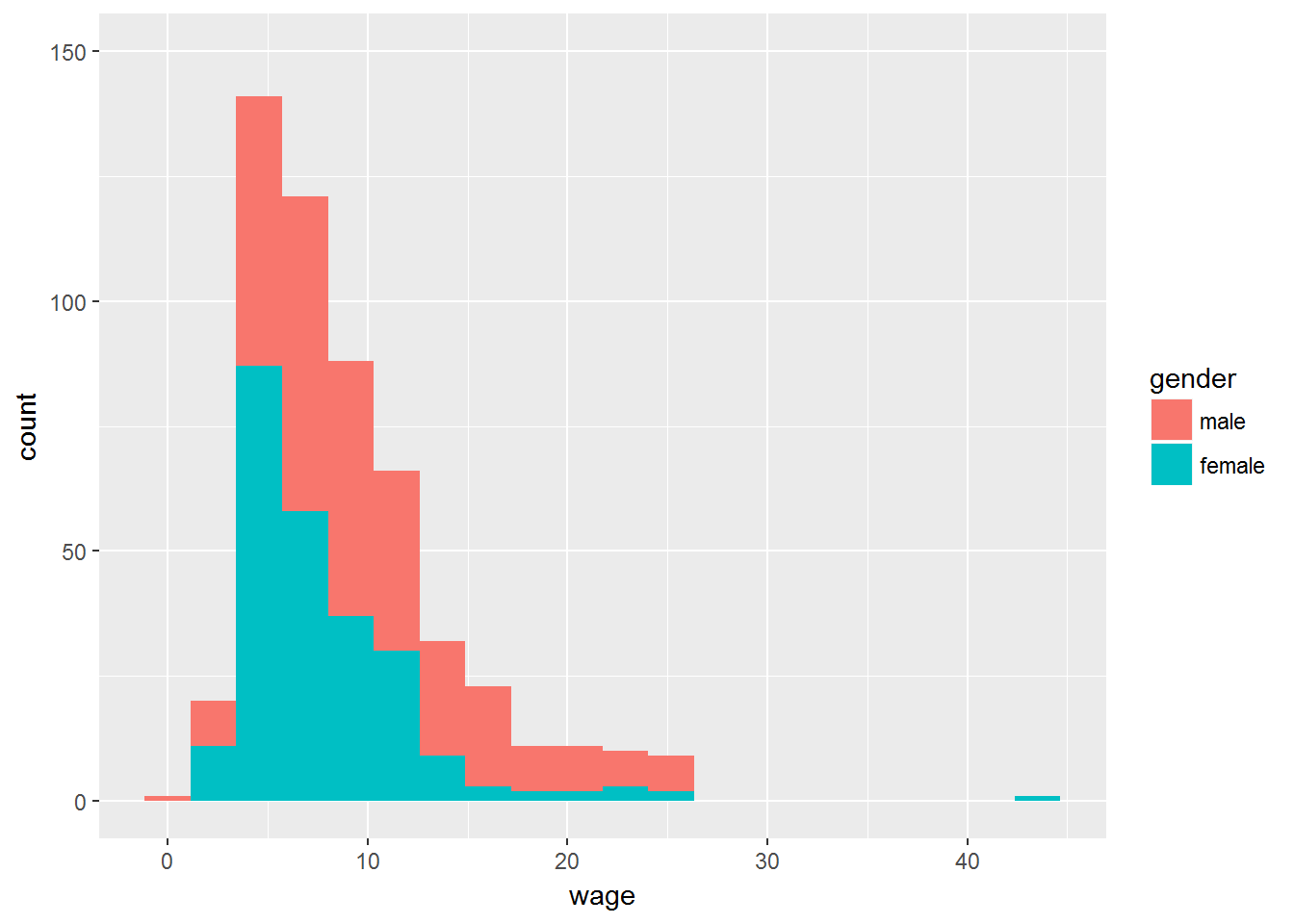
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(bins=20, aes(fill=gender), position="fill", alpha=0.4) +
labs(x= "Salario", y="Empleados", fill="Género") + # títulos de ejes y leyenda
scale_fill_discrete(labels=c("Hombre","Mujer")) # títulos claves leyenda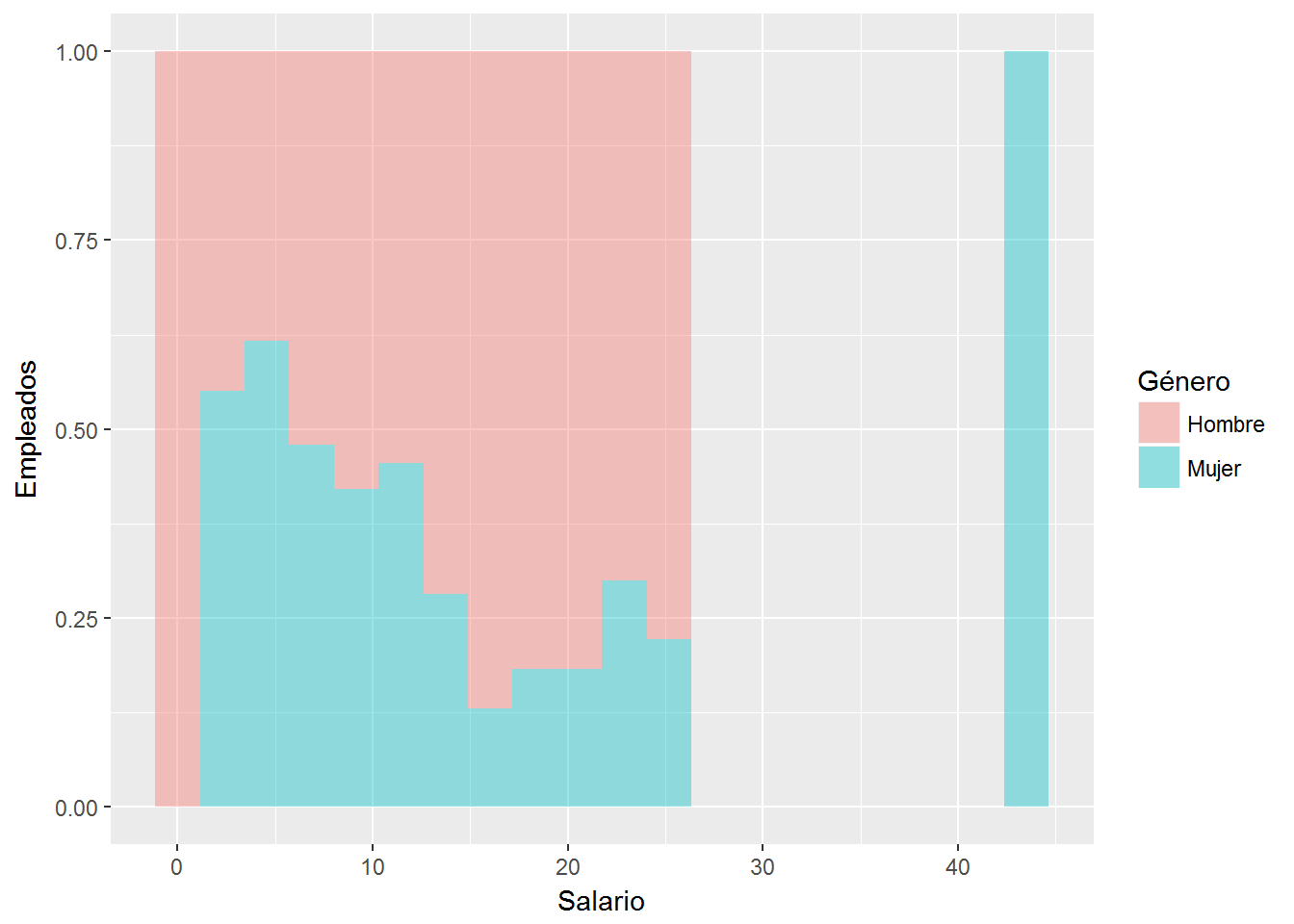
- Representamos los polígonos de frecuencias de los distintos grupos.
ggplot(CPS1985, aes(x=wage)) +
geom_freqpoly(bins=20, aes(color=gender)) +
labs(color="Género")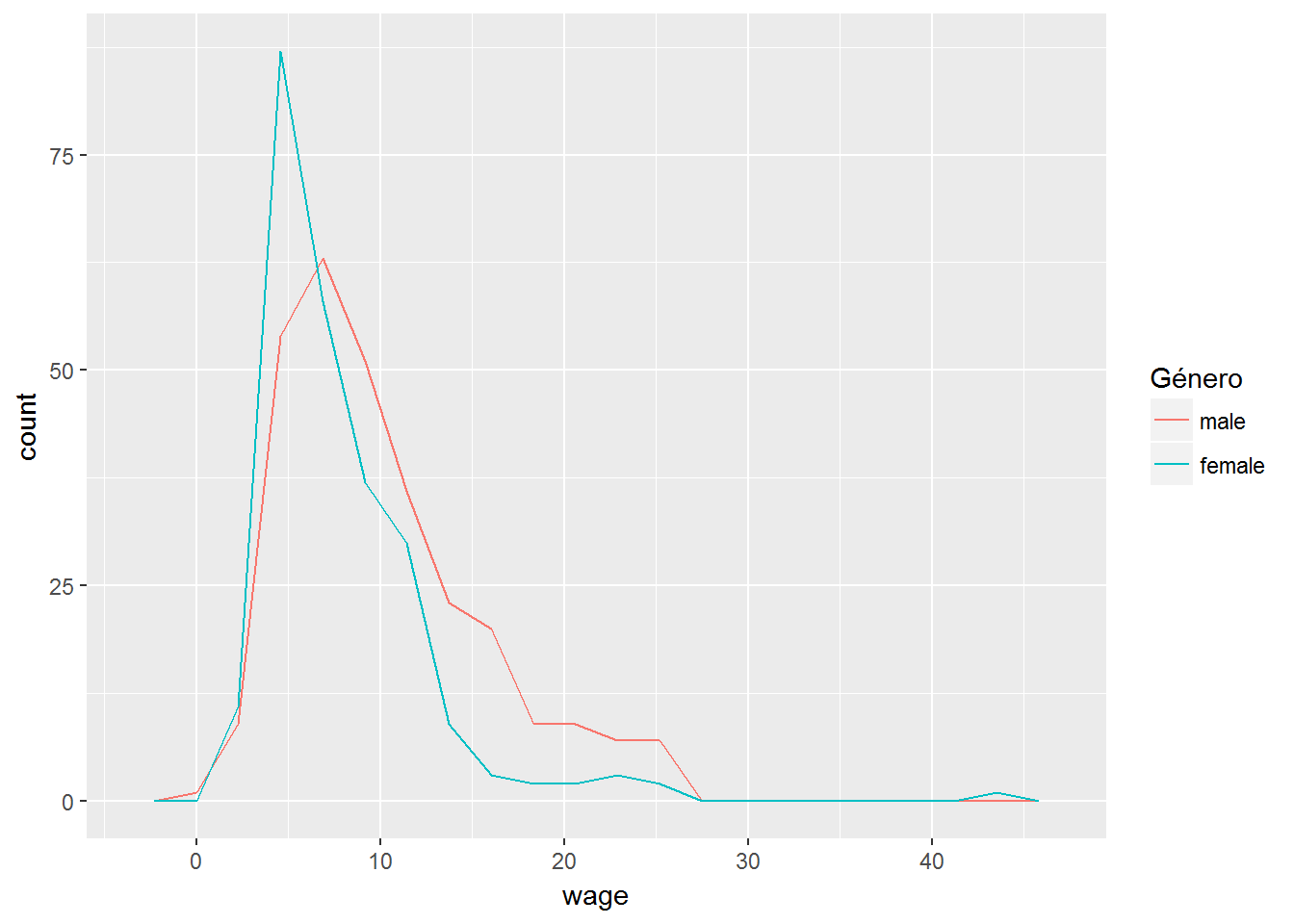
y casi mejor con la densidad de frecuencias:
ggplot(CPS1985, aes(x=wage)) +
geom_freqpoly(bins=20, aes(y=..density.., color=gender)) +
labs(color="Género")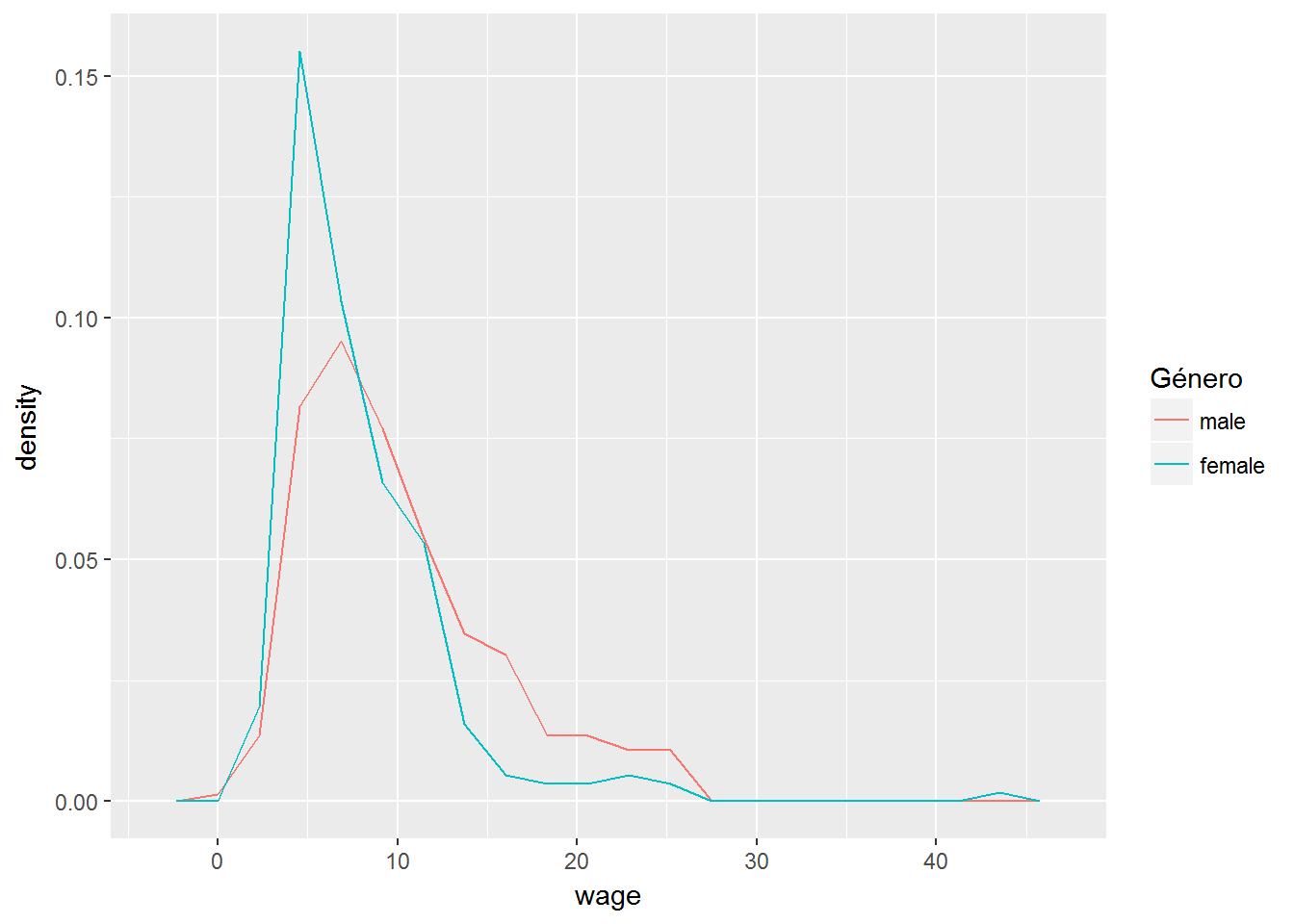
A continuación, vamos a añadir dos líneas para situar la media y la mediana.
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(aes(fill=..count..), bins=20, color="white") +
geom_vline(aes(xintercept=mean(wage)), color="red") +
geom_vline(aes(xintercept=median(wage)), color= "darkgreen") +
labs(title = "Distribución del salario (dólares por hora)",
x = "Salario",
y = "Número de empleados") +
scale_fill_continuous(name="Empleados") +
theme_classic() 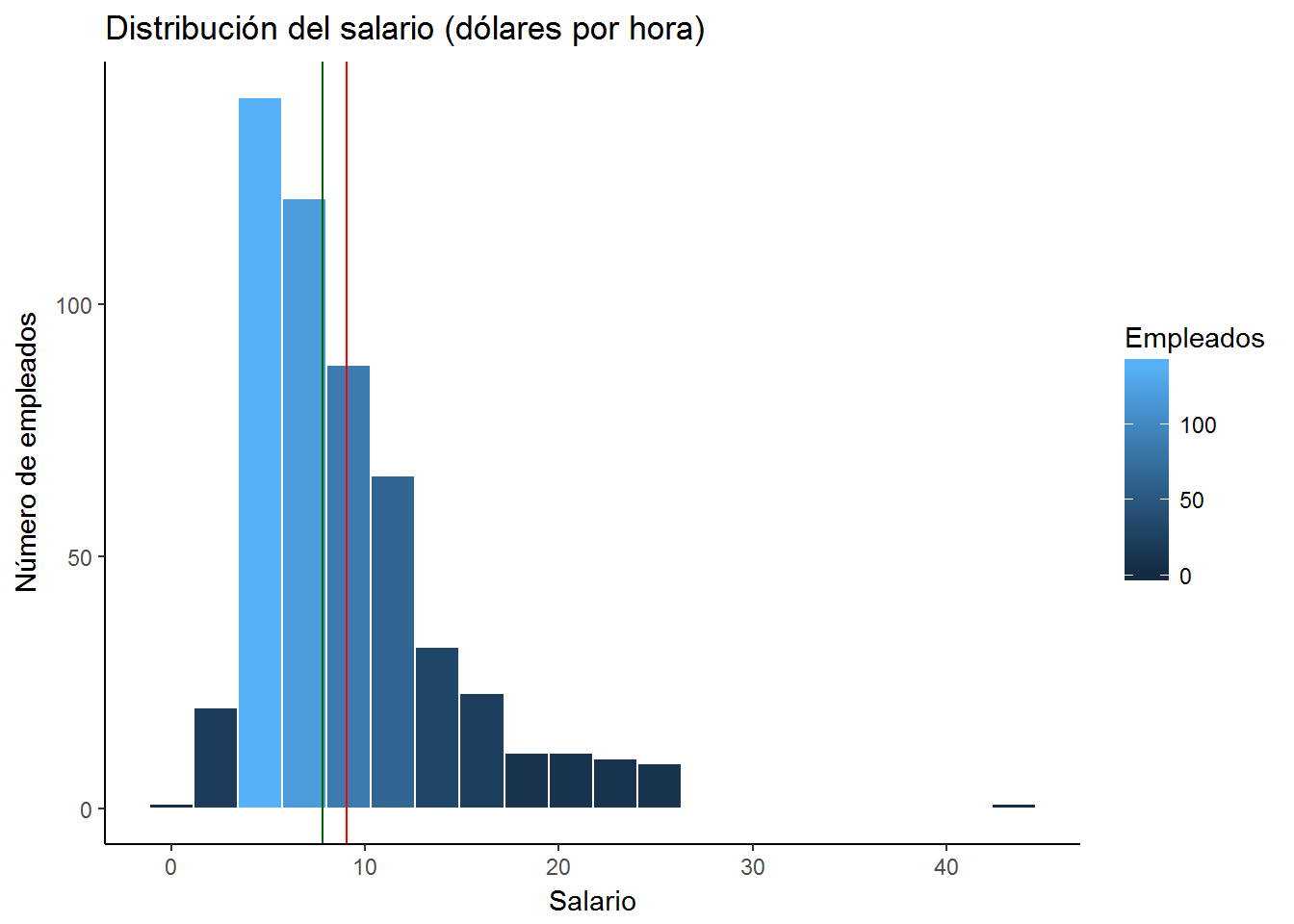
Añadimos la curva normal al histograma
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(aes(y=..density..), bins=20, color="white", fill="grey") +
stat_function(fun = dnorm, colour = "red",
arg = list(mean = mean(wage, na.rm = TRUE),
sd = sd(wage, na.rm = TRUE))) +
geom_density(color="blue")
Con el argumento expand_limits podemos evitar que la curva de densidad aparezca unida. Veámoslo con el siguiente ejemplo:
ggplot(CPS1985, aes(x=wage)) +
geom_histogram(aes(y=..density..), bins=20, color="white", fill="grey") +
stat_function(fun = dnorm, colour = "red",
arg = list(mean = mean(wage, na.rm = TRUE),
sd = sd(wage, na.rm = TRUE))) +
geom_line(stat="density", color="blue") +
expand_limits(y=0)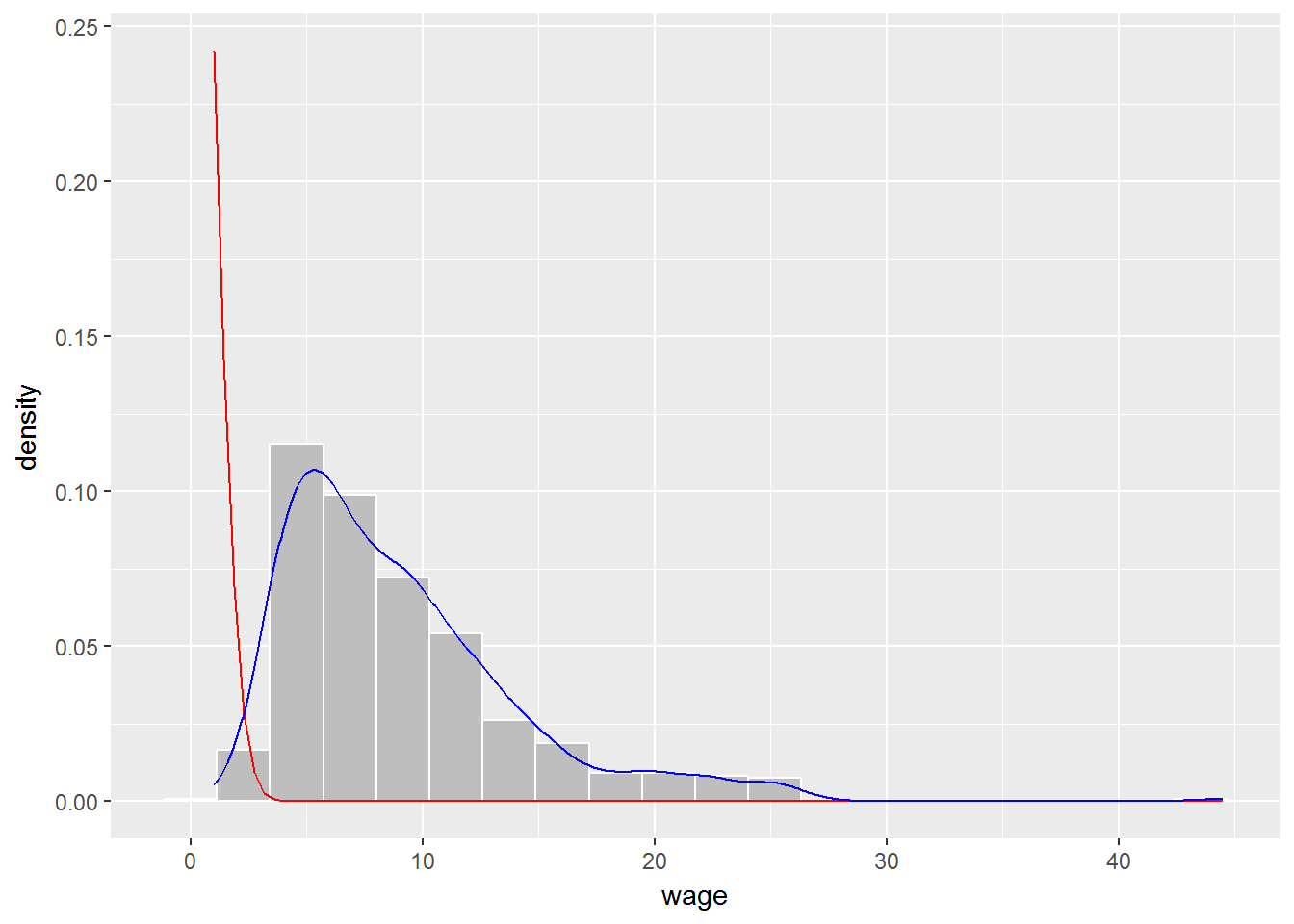
Podéis consultar las siguientes dos páginas web para aprender más sobre cómo crear histogramas con ggplot2:
Ahora, ha llegado el momento de que practiquéis lo visto en este apartado del tutorial. Vamos con la siguiente tarea:
- Tarea: Representad la distribución del salario (en logaritmos: log(wage)) mediante un histograma. Comparad la distribución de log(wage) según la raza (ethnicity).
Diagramas de caja
Para realizar un diagrama de caja utilizamos la geometría: geom_boxplot().
ggplot(CPS1985, aes(x=gender, y=wage)) +
geom_boxplot()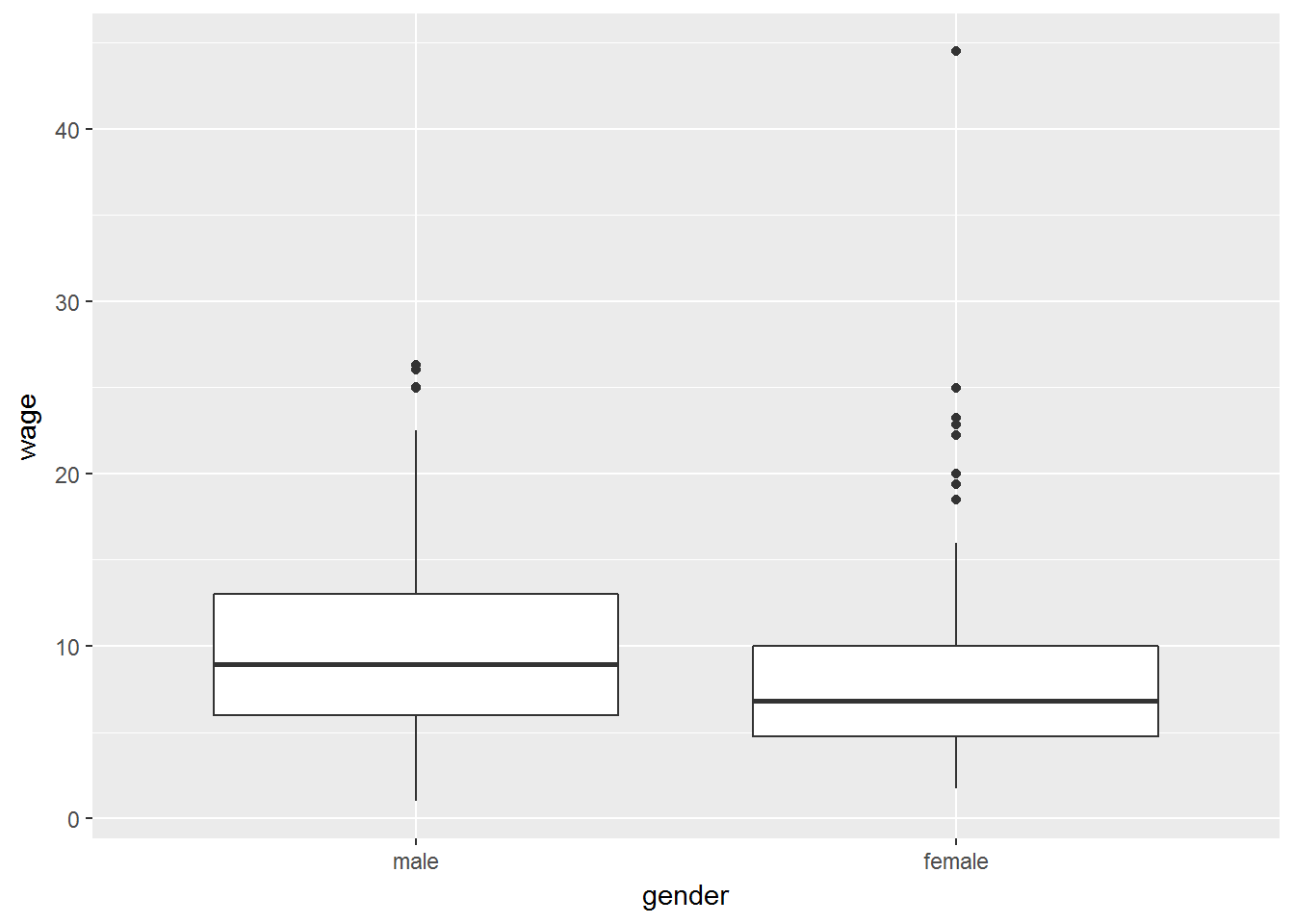
Podemos colorear las cajas del gráfico incluyendo en las características estéticas la variable que utilizaremos para el relleno. Automáticamente se crea una leyenda para facilitar la lectura del gráfico, que podemos cambiar de posición o eliminar si se considera que no aporta información relevante.
# Diagrama de caja con color de relleno
ggplot(CPS1985, aes(x=gender, y=wage, fill=gender)) +
geom_boxplot() +
labs(x="Género", y="Salario", fill="Género") + # titulo ejes y leyenda
scale_x_discrete(labels=c("Hombre","Mujer")) + # etiquetas del eje x
scale_fill_discrete(labels=c("Hombre","Mujer")) # etiquetas claves leyenda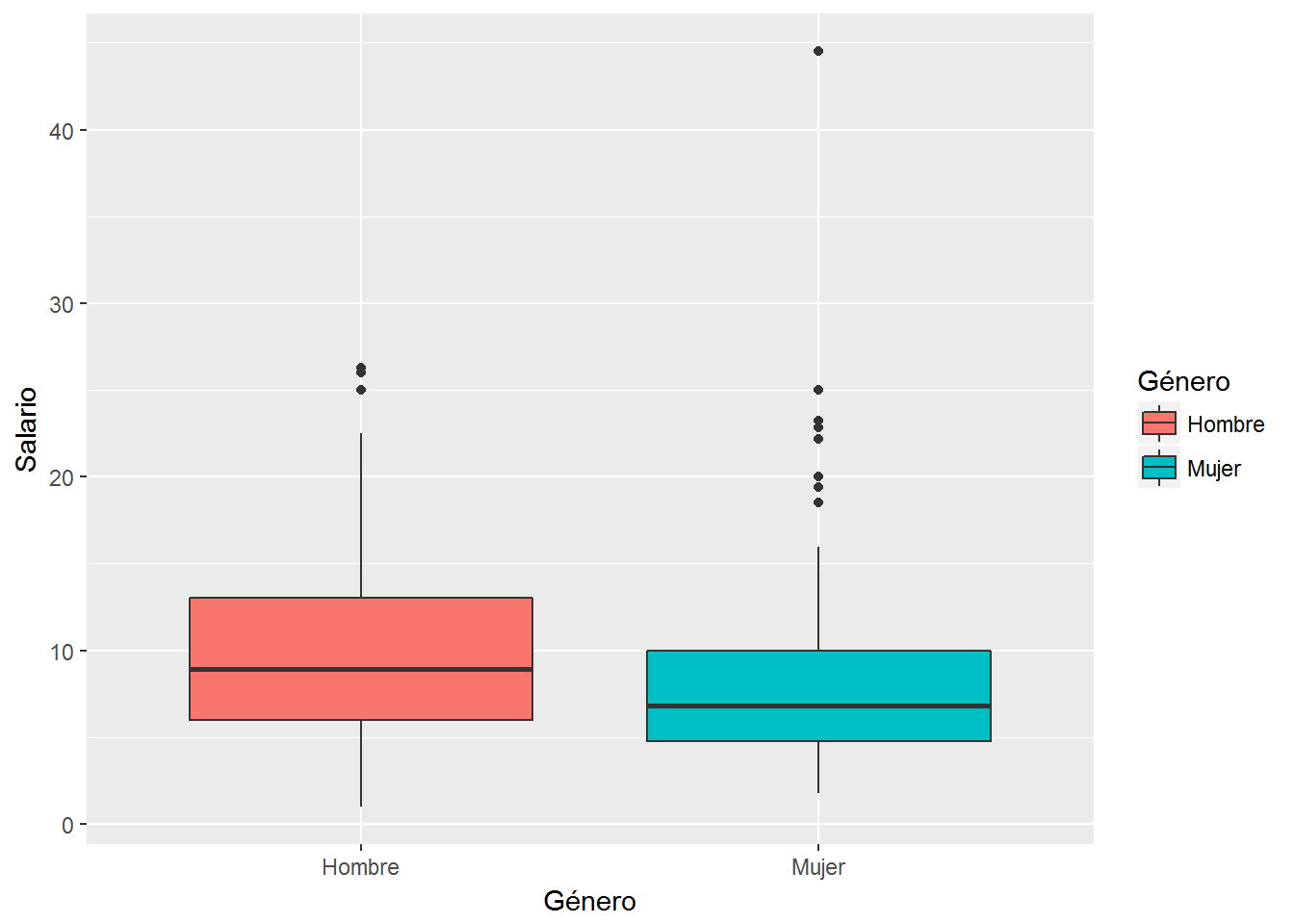
# Diagrama de caja con cambio de posición de la leyenda
ggplot(CPS1985, aes(x=gender, y=wage, fill=gender)) +
geom_boxplot() +
labs(x="Género", y="Salario", fill="Género") +
scale_x_discrete(labels=c("Hombre","Mujer")) +
scale_fill_discrete(labels=c("Hombre","Mujer")) +
theme(legend.position="top") # cambio posición de leyenda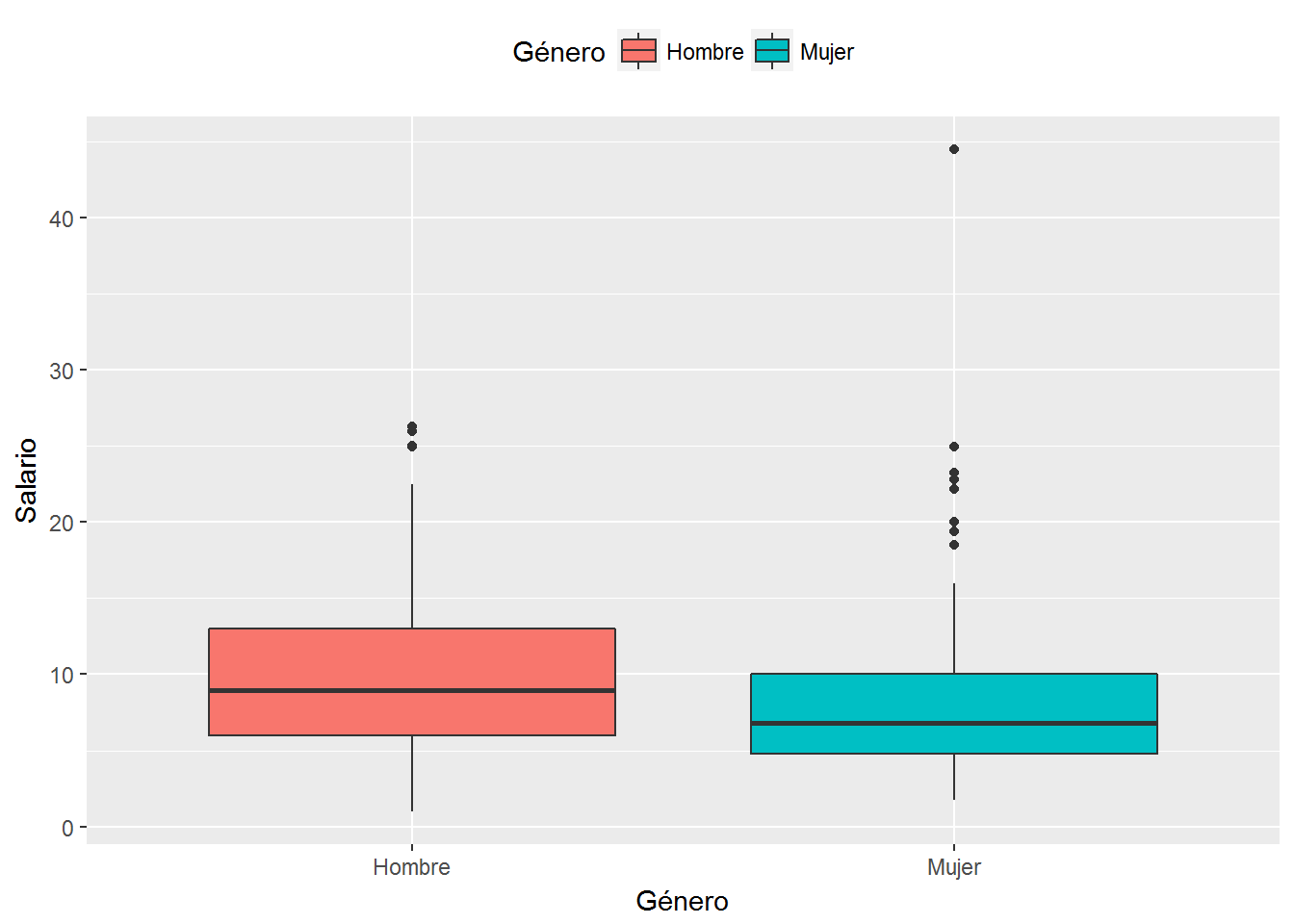
# Diagrama de caja sin leyenda por considerar redundante la información
ggplot(CPS1985, aes(x=gender, y=wage, fill=gender)) +
geom_boxplot(outlier.colour = "blue") + # color de los outliers
labs(x="Género", y="Salario") +
scale_x_discrete(labels=c("Hombre","Mujer")) +
guides(fill=FALSE) # eliminamos la leyenda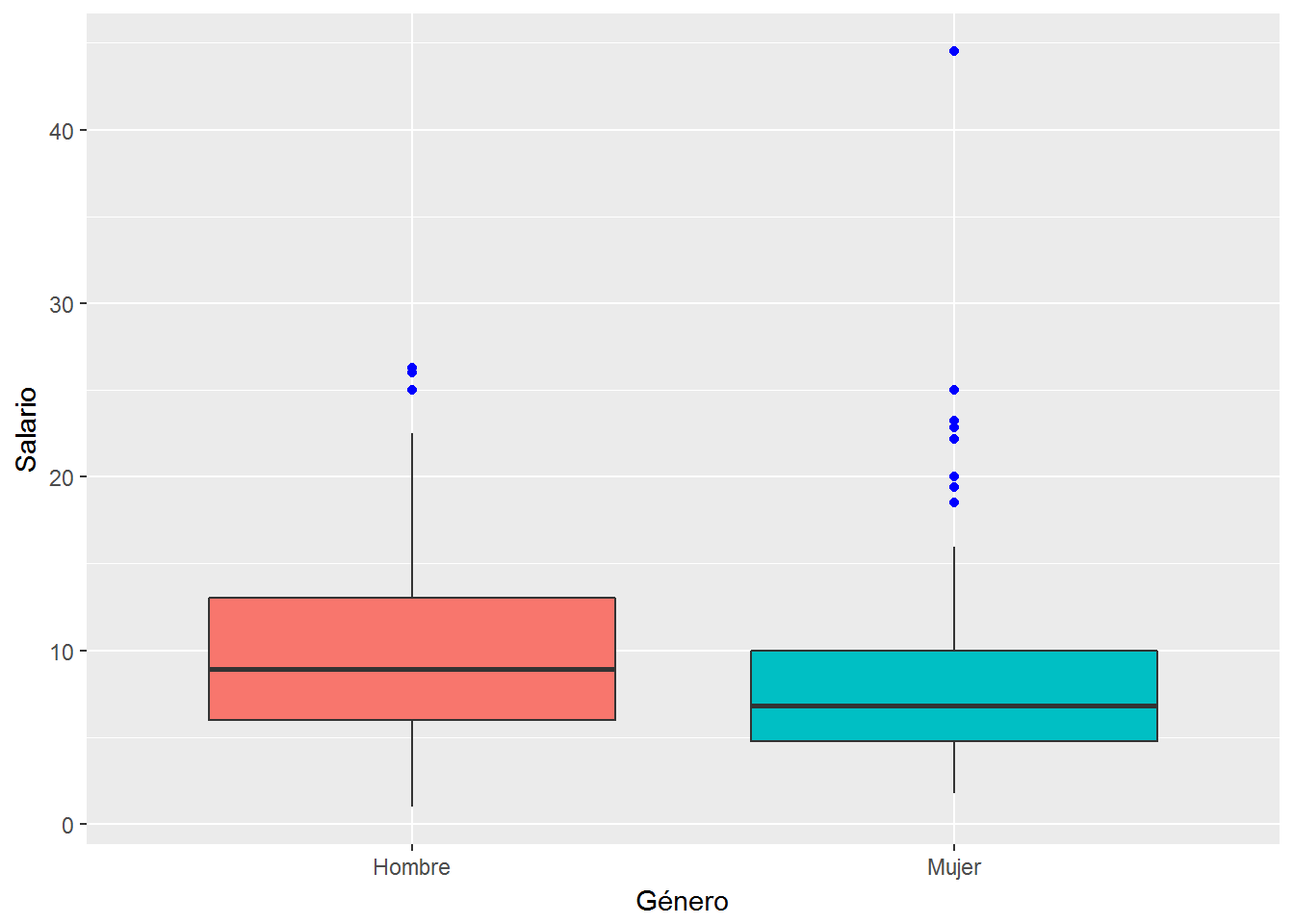
Para cambiar la orientación de las cajas y que en lugar de representarse verticalmente se representen horizontalmente se utiliza la función coord_flip(). Esta forma de presentar los diagramas de caja es muy frecuente porque facilita la interpretación de los mismos al situar la variable cuantitativa en el eje de abscisas.
ggplot(CPS1985, aes(x=gender, y=wage, fill=gender)) +
geom_boxplot(outlier.colour = "blue") +
labs(x="Género", y="Salario") +
scale_x_discrete(labels=c("Hombre","Mujer")) +
guides(fill=FALSE) +
coord_flip() # cambio dirección de las cajas
Puede resultar interesante localizar la media de cada grupo en los diagramas de caja. Para ello, hacemos uso del elemento stat (transformación estadística). Se puede añadir stat, básicamente, de dos formas:
- añadir directamente una función stat_() y de esa forma anular su valor por defecto en la geometría.
- añadir una función geom_() e introducir el elemento stat para anular el valor por defecto.
Veamos las dos formas comentadas de añadir .
# Añadimos la media utilizando la función stat_()
ggplot(CPS1985, aes(x=gender, y=wage, fill=gender)) +
geom_boxplot() +
labs(x="Género", y="Salario") +
scale_x_discrete(labels=c("Hombre","Mujer")) +
guides(fill=FALSE) +
coord_flip() +
stat_summary(fun.y=mean, geom="point", shape=5, size=4)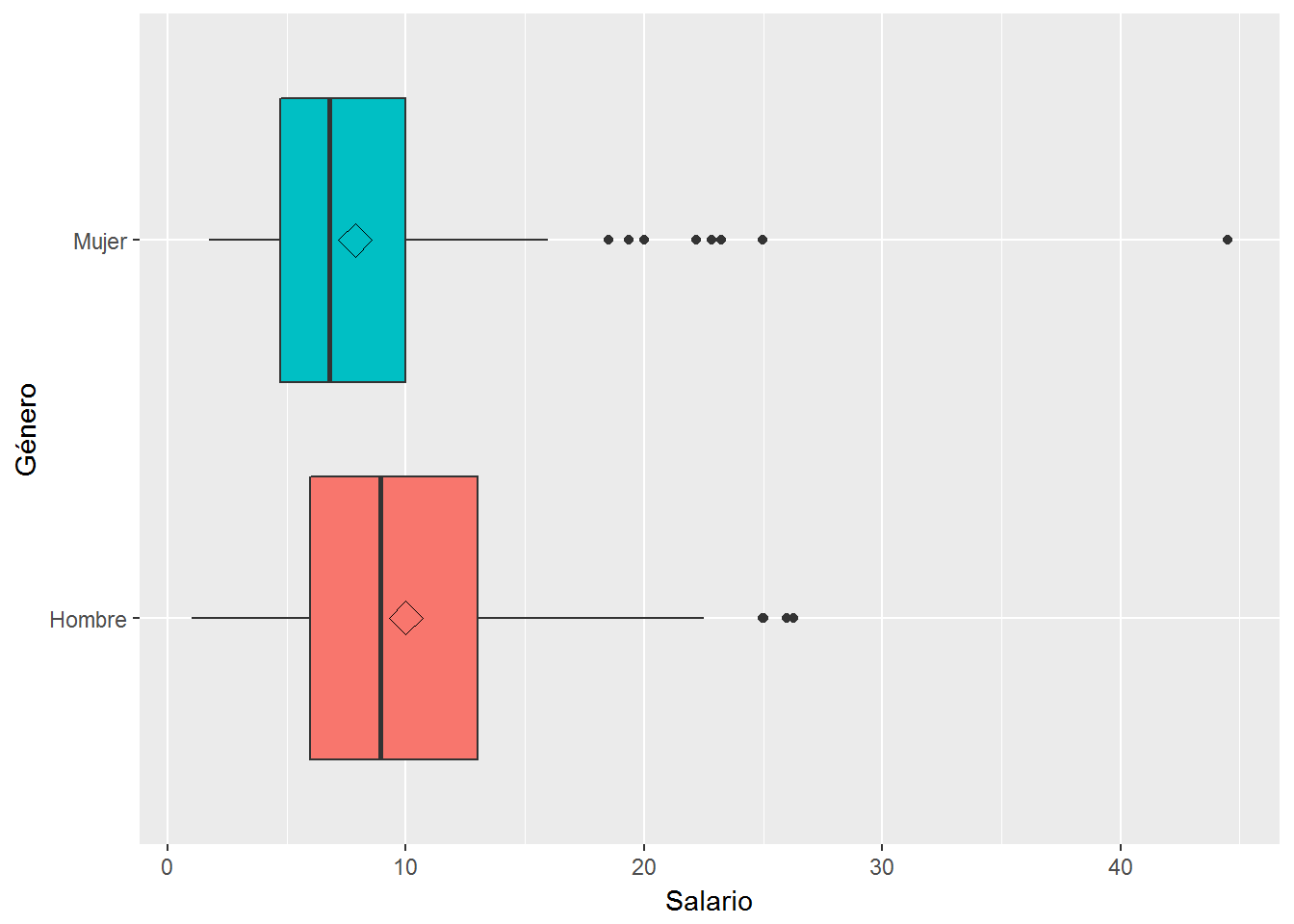
# Añadimos la media utilizando la función geom_() y modificando el elemento stat
ggplot(CPS1985, aes(x=gender, y=wage, fill=gender) ) +
geom_boxplot(alpha=0.3, outlier.colour = "blue") +
labs(x="Género", y="Salario") +
scale_x_discrete(labels=c("Hombre","Mujer")) +
guides(fill=FALSE) +
coord_flip() +
geom_point(stat= "summary", fun.y=mean, shape=16, size=2, color="red")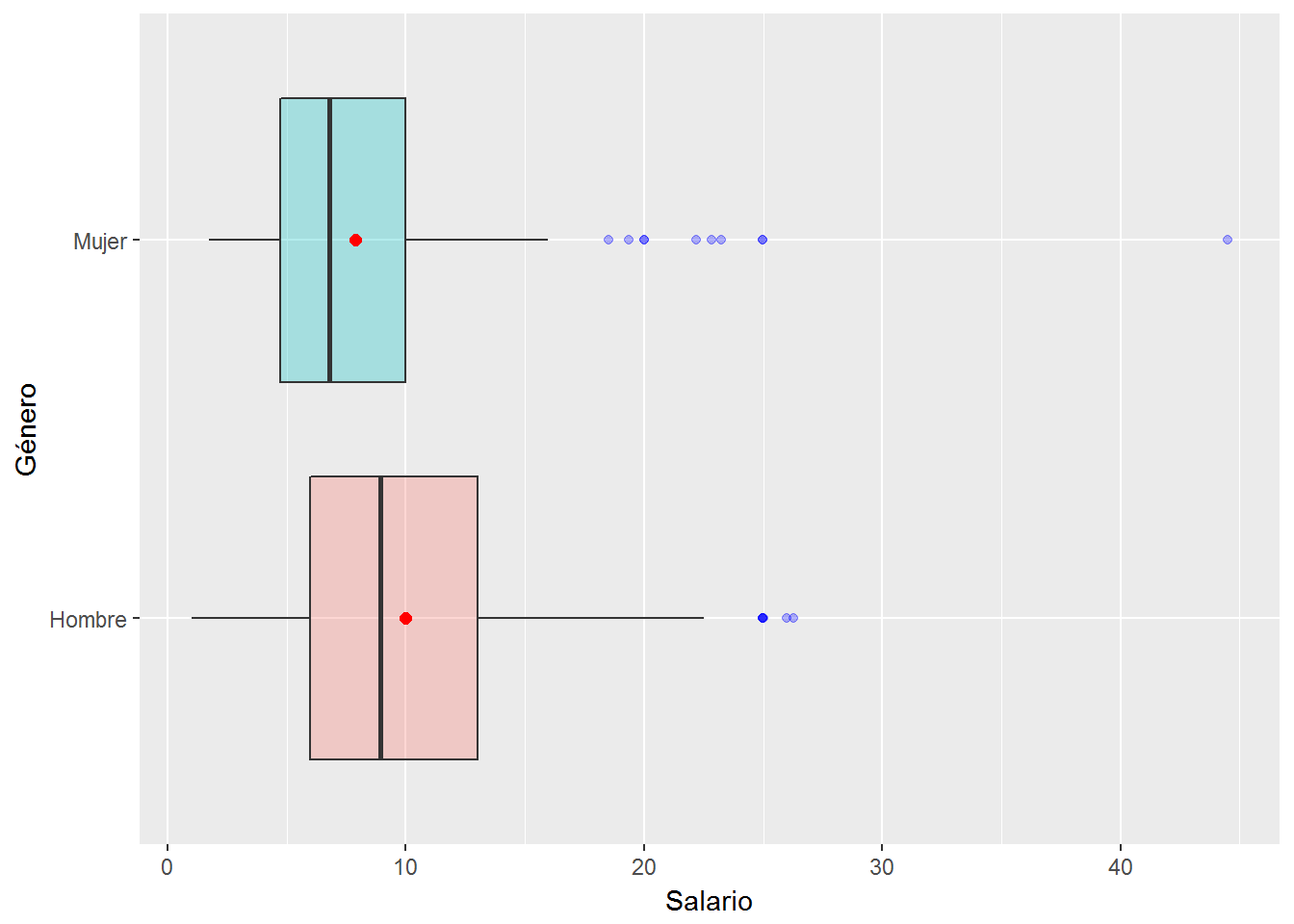
Por último, si queremos hacernos una idea de cómo se distribuyen nuestras observaciones/individuos respecto del diagrama de caja podemos hacer uso de la función position_jitter(). Cuando hay muchos datos las observaciones se superponen. La función position_jitter() lo que hace es añadir un pequeño “ruido” en cada posición. También podemos utilizar la geometría geom_jitter(). A continuación se muestran los diagramas de caja con estas dos opciones.
ggplot(CPS1985, aes(x=gender, y=wage, fill=gender) ) +
geom_boxplot(alpha=0.3, outlier.colour = "blue") +
labs(x="Género", y="Salario") +
scale_x_discrete(labels=c("Hombre","Mujer")) +
guides(fill=FALSE) +
coord_flip() +
geom_point(stat= "summary", fun.y=mean, shape=16, size=4, color="red") +
geom_point(position = position_jitter(width = 0.1), alpha = 0.2)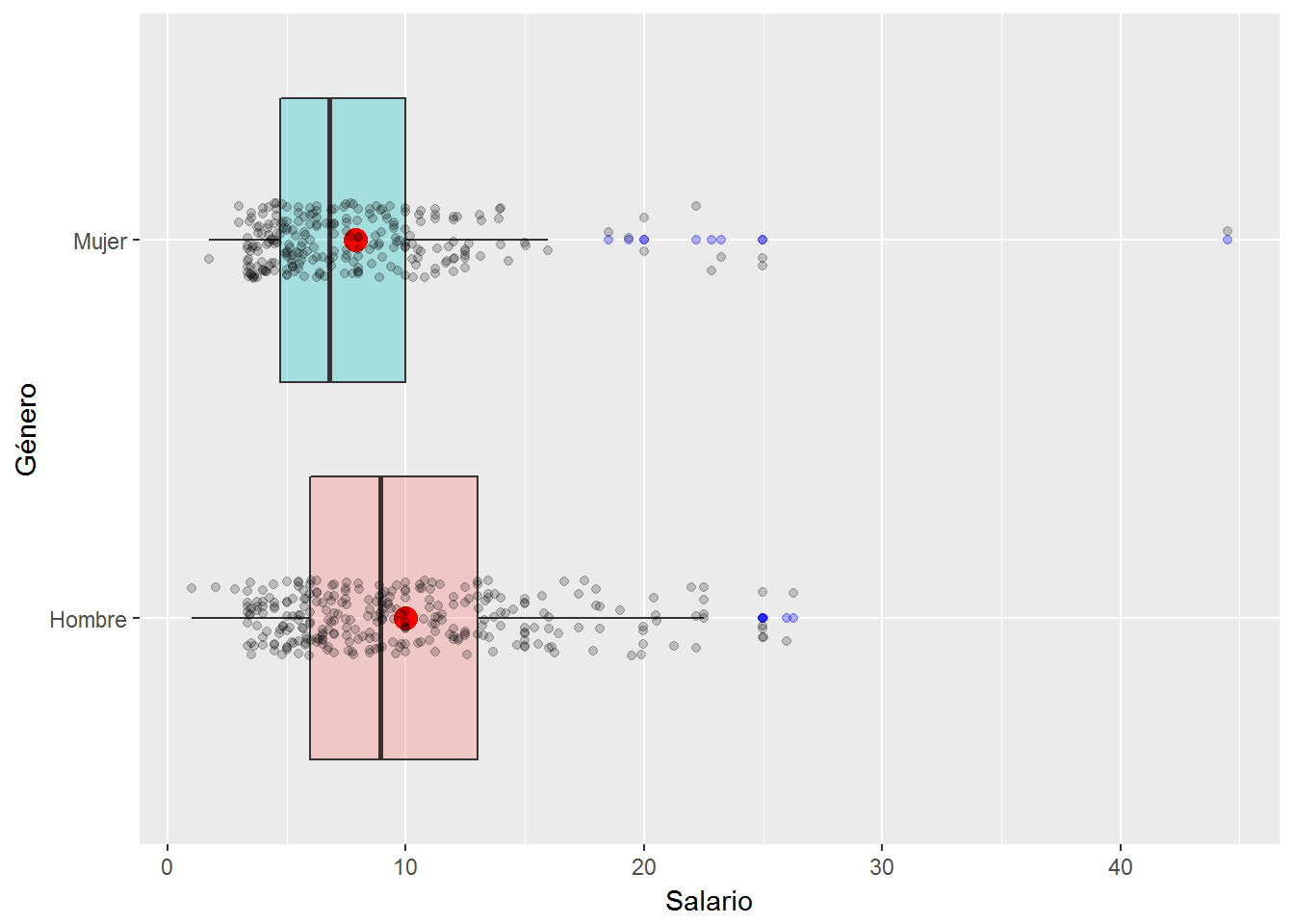
ggplot(CPS1985, aes(x=gender, y=wage, fill=gender) ) +
geom_boxplot(alpha=0.3, outlier.colour = "blue") +
labs(x="Género", y="Salario") +
scale_x_discrete(labels=c("Hombre","Mujer")) +
guides(fill=FALSE) +
coord_flip() +
geom_point(stat= "summary", fun.y=mean, shape=16, size=4, color="red") +
geom_jitter(width = 0.1, alpha = 0.2)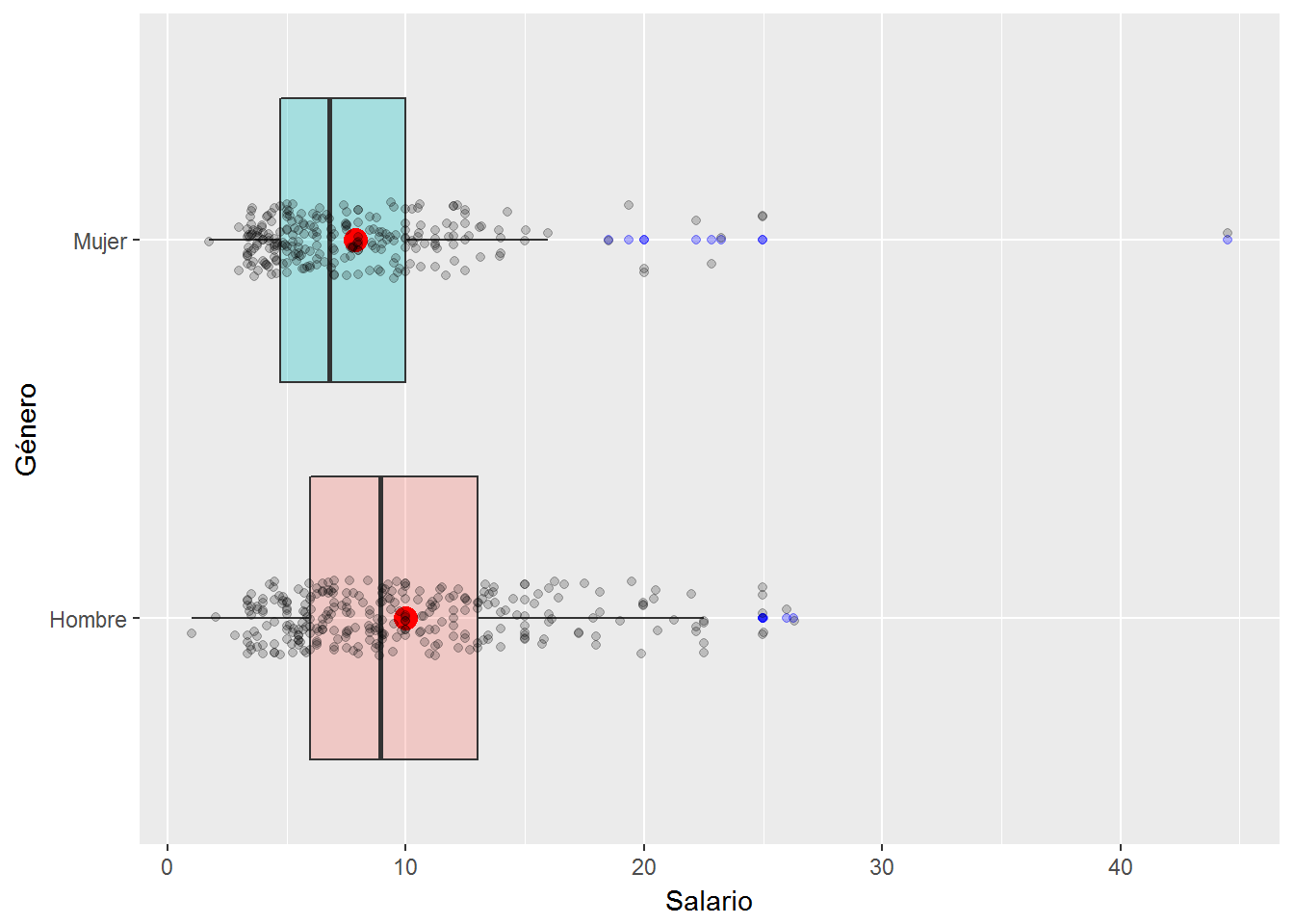
Para practicar lo aprendido proponemos la siguiente tarea:
- Tarea: Representad el diagrama de caja del salario (wage) en función de la ocupación (occupation). Incorporad al gráfico toda la información que se considere oportuna.
Diagramas de dispersión
Ya hemos visto a lo largo de este tutorial que el salario presenta una gran dispersión y su distribución es asimétrica. Sin embargo, si transformamos el salario y trabajamos con el logaritmo del salario, tanto la dispersión como la asimetría se reducen. Cuando trabajamos con variables monetarias esta situación suele ser frecuente y, por tanto, normalmente se trabaja con logaritmos.
¿Cómo es la relación entre el salario (en logaritmos) y la experiencia?
Hacemos el diagrama de dispersión para ver la posible relación entre ambas variables.
ggplot(CPS1985, aes(experience, log(wage))) +
geom_point() +
labs(title="Diagrama de dispersión",
subtitle= "ScatterPlot",
caption="Fuente: CPS1985 (paquete AER)",
x="Experiencia (en años)",
y="Salario (en logaritmo)")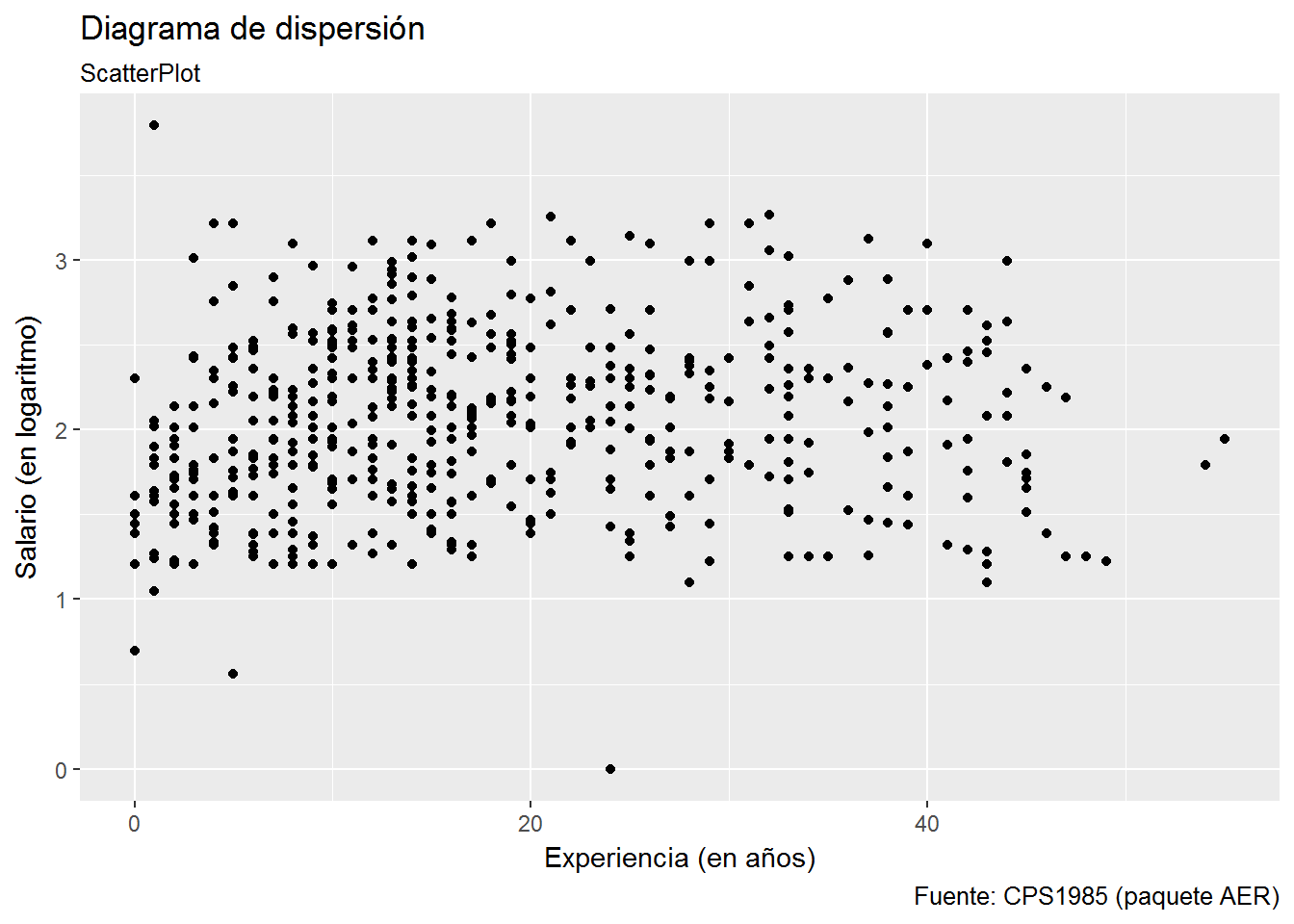
Si queremos que los puntos del diagrama de dispersión tengan color tenemos varias alternativas. Observar las diferencias entre los siguientes tres gráficos.
# Opción 1
ggplot(CPS1985, aes(experience, log(wage), color="red")) +
geom_point()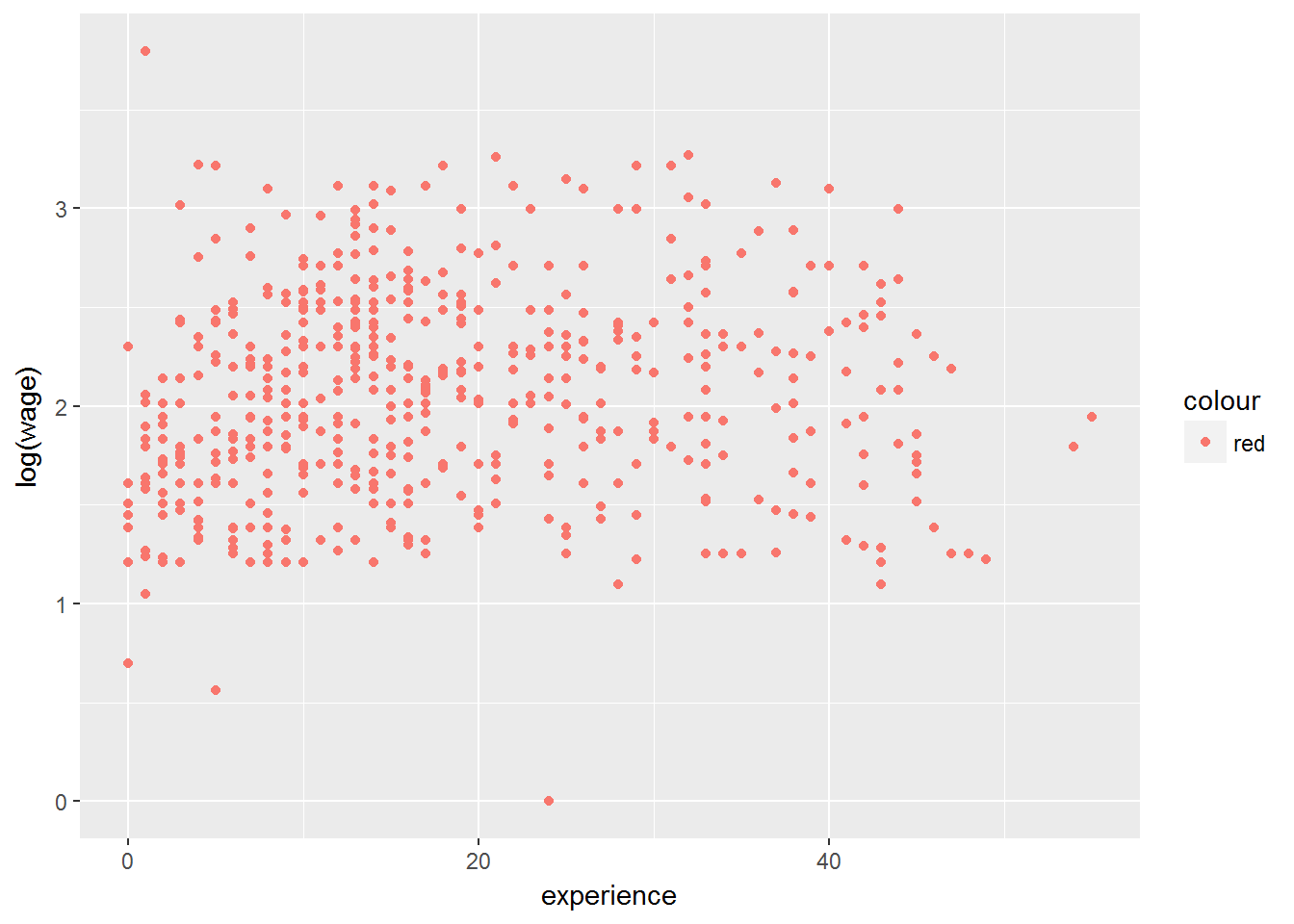
# Opción 2
ggplot(CPS1985, aes(experience, log(wage))) +
geom_point(aes(color="red"))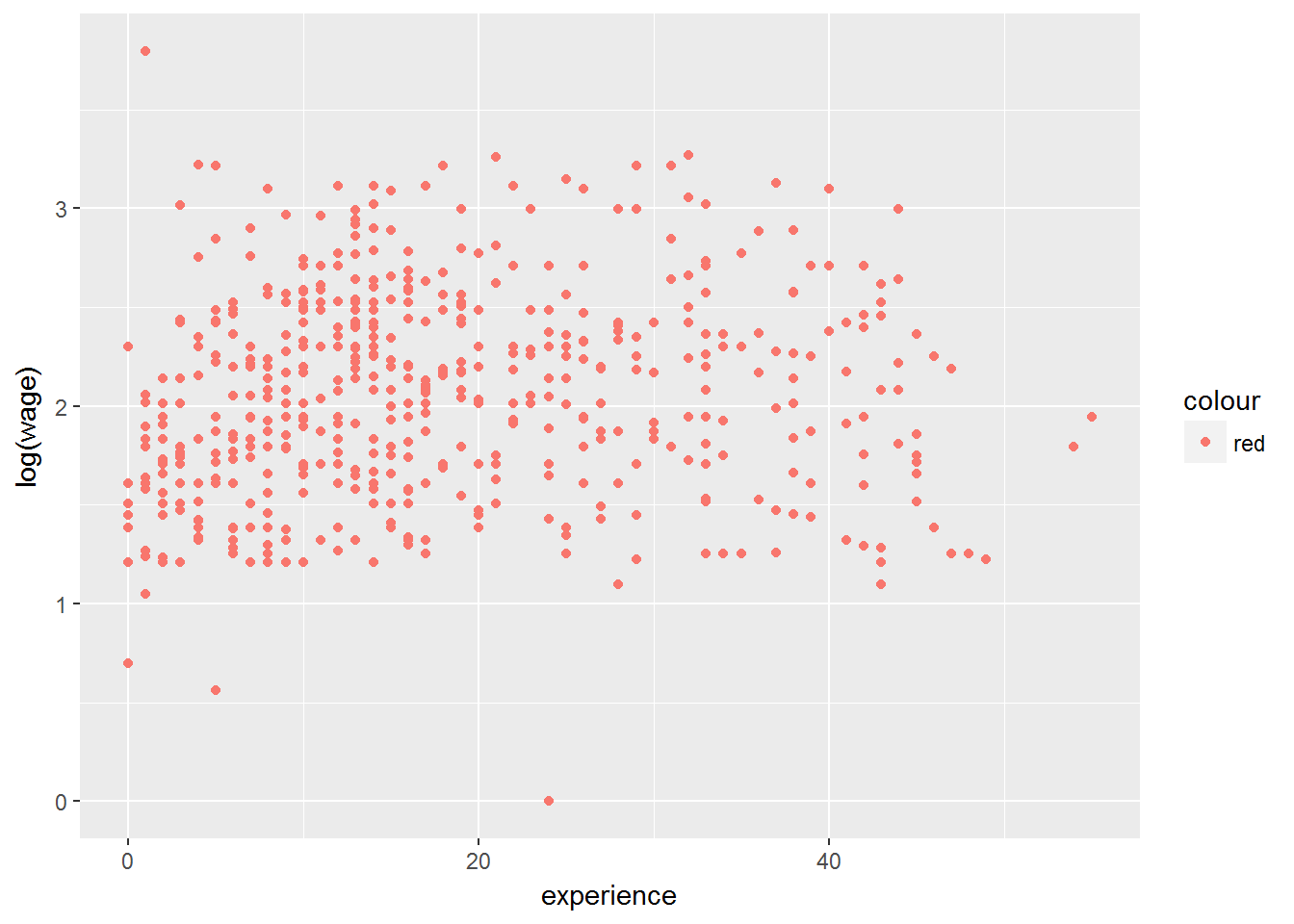
# Opción 3
ggplot(CPS1985, aes(experience, log(wage))) +
geom_point(color="red")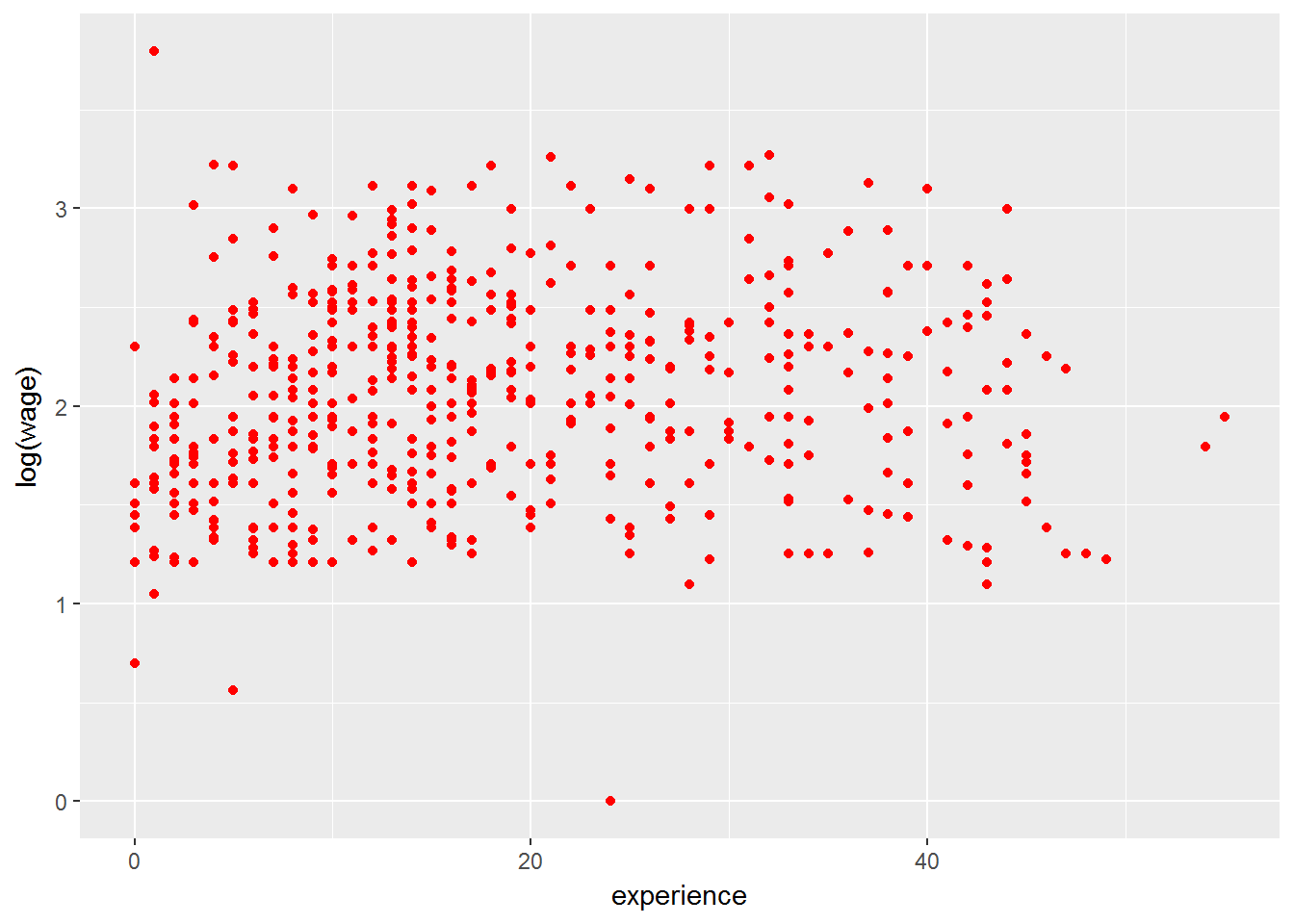
Las dos primeras opciones -en las que color se ha introducido como una característica estética (con aes())- tienen un efecto similar (no igual, más tarde lo veremos): se crea una variable color que toma el valor red y automáticamente se muestra una leyenda. En la tercera opción el color se introduce como una constante.
Si tenemos muchos datos es muy probable que se produzca un importante solapamiento de las observaciones. Si “muchos datos” no son “muchísimos”, podemos utilizar jitter para introducir una pequeña perturbación en las observaciones y mejorar la visualización de los datos con el diagrama de dispersión.
ggplot(CPS1985, aes(experience,log(wage))) +
geom_jitter(width=.2, alpha=0.5) +
labs(title="Diagrama de dispersión",
subtitle= "ScatterPlot",
caption="Fuente: CPS1985 (paquete AER)",
x="Experiencia (en años)",
y="Salario (en logaritmo)")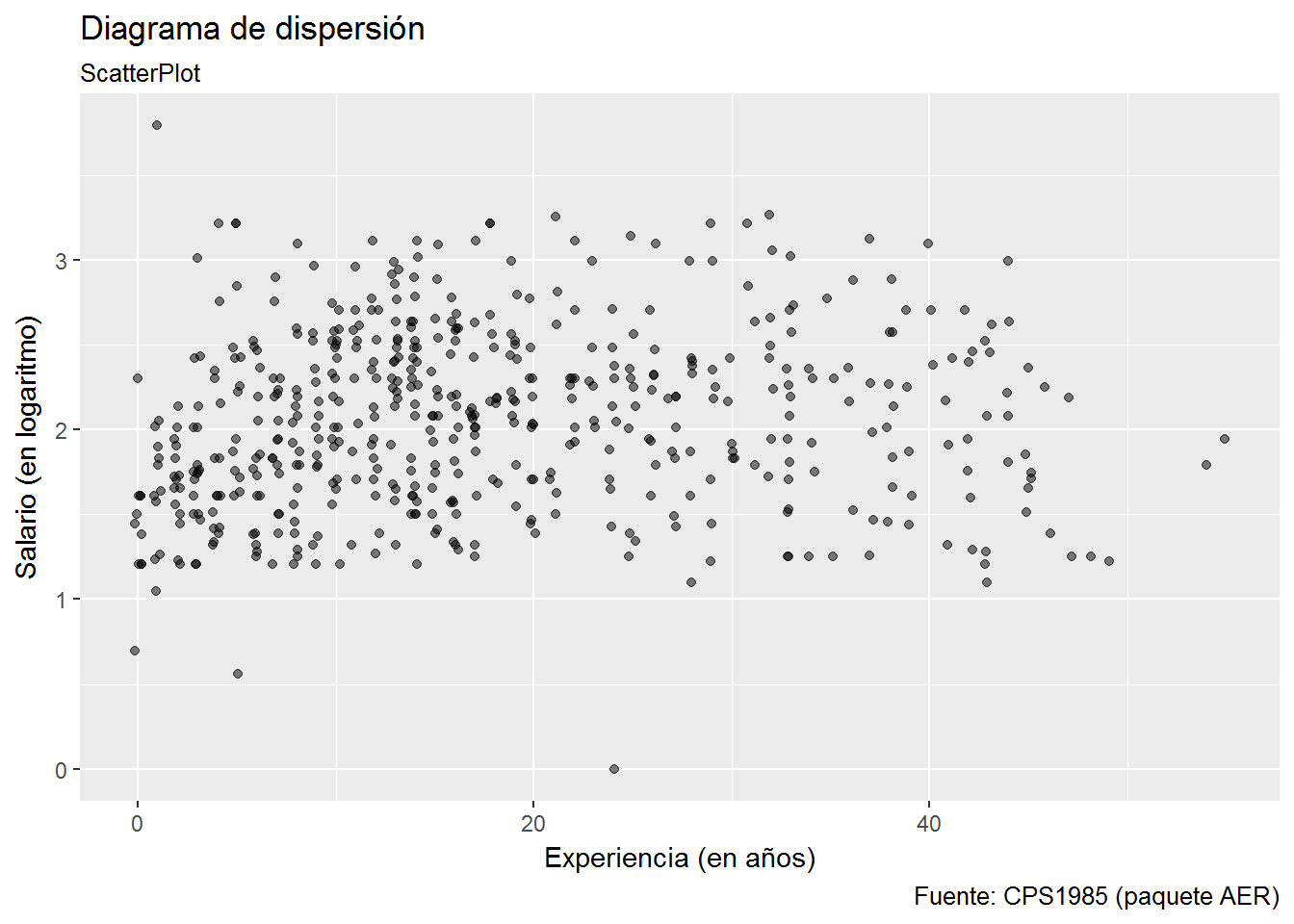
Una alternativa al gráfico anterior es representar lo que se conoce como Hex plot. Este gráfico es equivalente a un histograma en el sentido que se representan puntos hexagonales con distinto color en función del número de observaciones que caen dentro de cada hexágono.
# install.packages("hexbin") # Hay que instalar el paquete hexbin
library(hexbin)
ggplot(CPS1985, aes(experience,log(wage))) +
geom_hex() +
labs(title="Diagrama de dispersión",
subtitle= "ScatterPlot",
caption="Fuente: CPS1985 (paquete AER)",
x="Experiencia (en años)",
y="Salario (en logaritmo)") +
scale_fill_continuous("Empleados") +
theme_classic()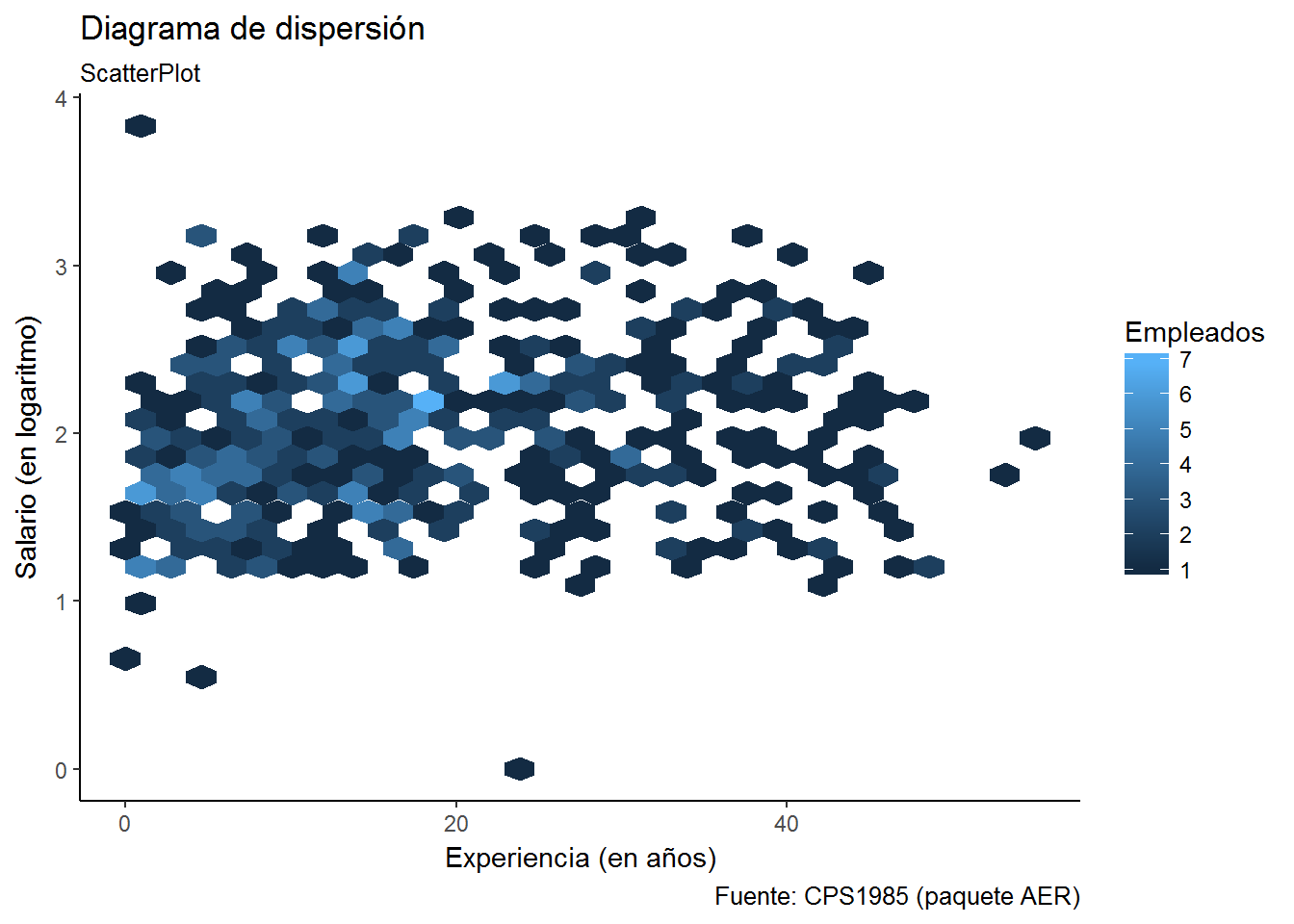
Cuando se utiliza la geometría geom_hex los puntos hexagonales se colorean, por defecto, según una escala gradual de tonos azules (azul oscuro equivale a poca frecuencia, azul claro equivale a alta frecuencia). Esto no es muy intuitivo para nosotros: ¿claro mucha frecuencia?, ¿oscuro poca frecuencia?. Al revés estamos más acostumbrados. Podemos cambiar la escala de colores utilizando la función scale_fill_gradient.
ggplot(CPS1985, aes(experience,log(wage))) +
geom_hex() +
labs(title="Diagrama de dispersión",
subtitle= "ScatterPlot",
caption="Fuente: CPS1985 (paquete AER)",
x="Experiencia (en años)",
y="Salario (en logaritmo)") +
scale_fill_gradient("Empleados", low="orange", high="orange4") + # nombres en colors()
theme_classic()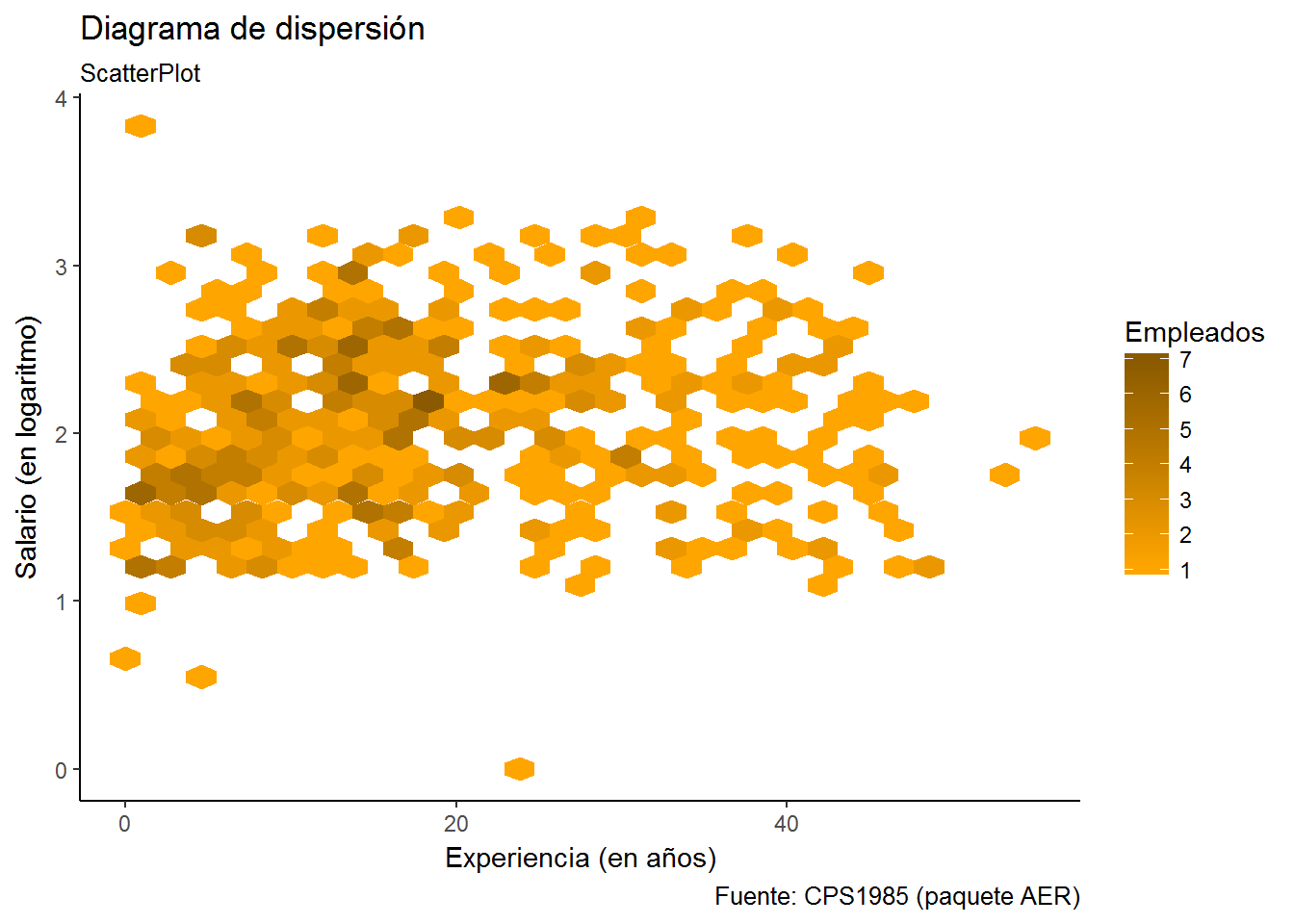
Ahora, en el diagrama de dispersión vamos a colorear los puntos según el género. Observar las diferencias entres los siguientes tres diagramas de dispersión. ¿Alguna diferencia entre los siguientes dos gráficos?
# Opción 1
ggplot(CPS1985, aes(experience,log(wage), color=gender)) +
geom_point() +
labs(title="Diagrama de dispersión",
subtitle= "ScatterPlot",
caption="Fuente: CPS1985 (paquete AER)",
x="Experiencia (en años)",
y="Salario (en logaritmo)") +
scale_color_discrete(name="Género", labels=c("Hombre","Mujer"))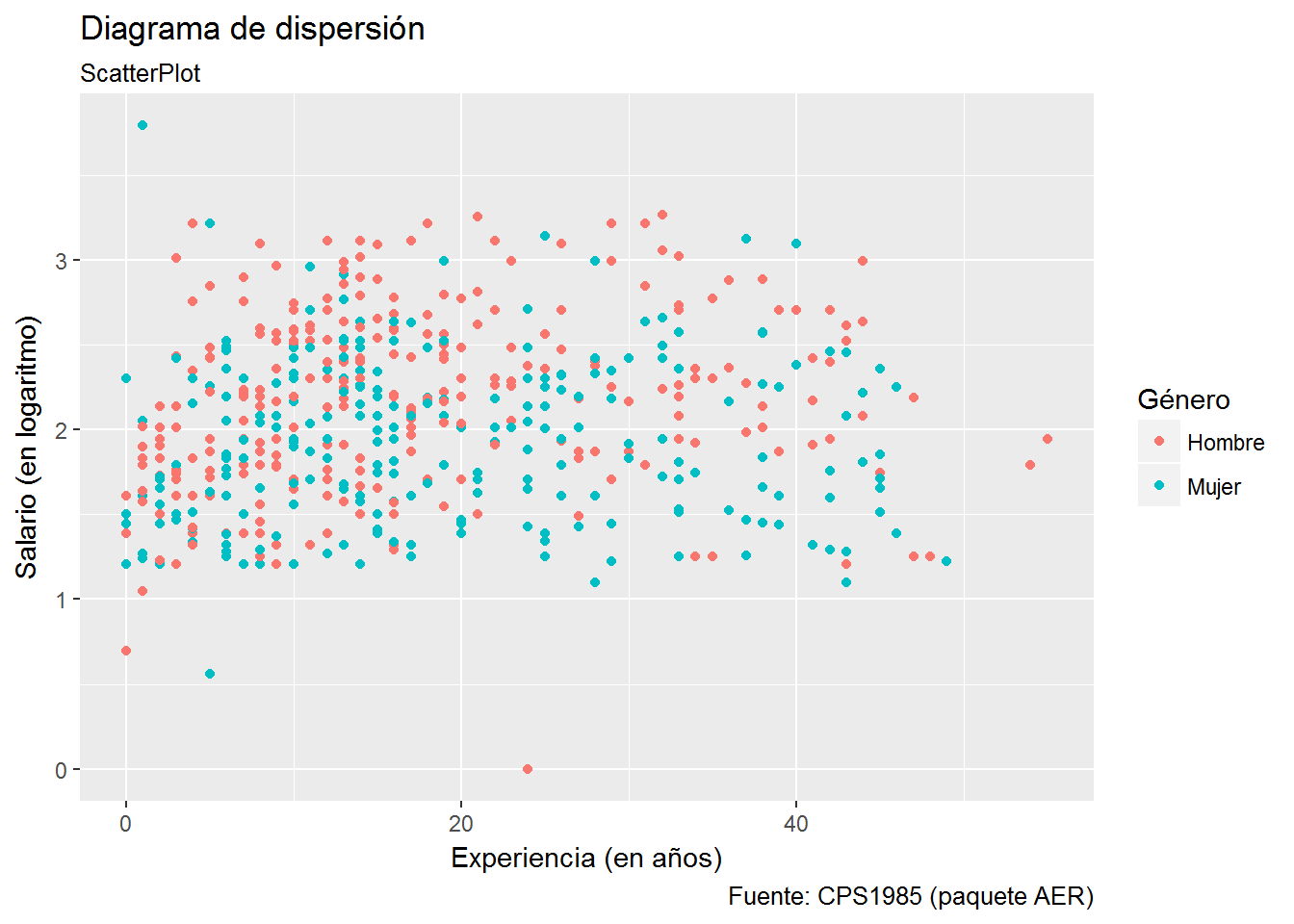
# Opción 2
ggplot(CPS1985, aes(experience,log(wage))) +
geom_point(aes(color=gender)) +
labs(title="Diagrama de dispersión",
subtitle= "ScatterPlot",
caption="Fuente: CPS1985 (paquete AER)",
x="Experiencia (en años)",
y="Salario (en logaritmo)") +
scale_color_discrete("Género", labels=c("Hombre","Mujer"))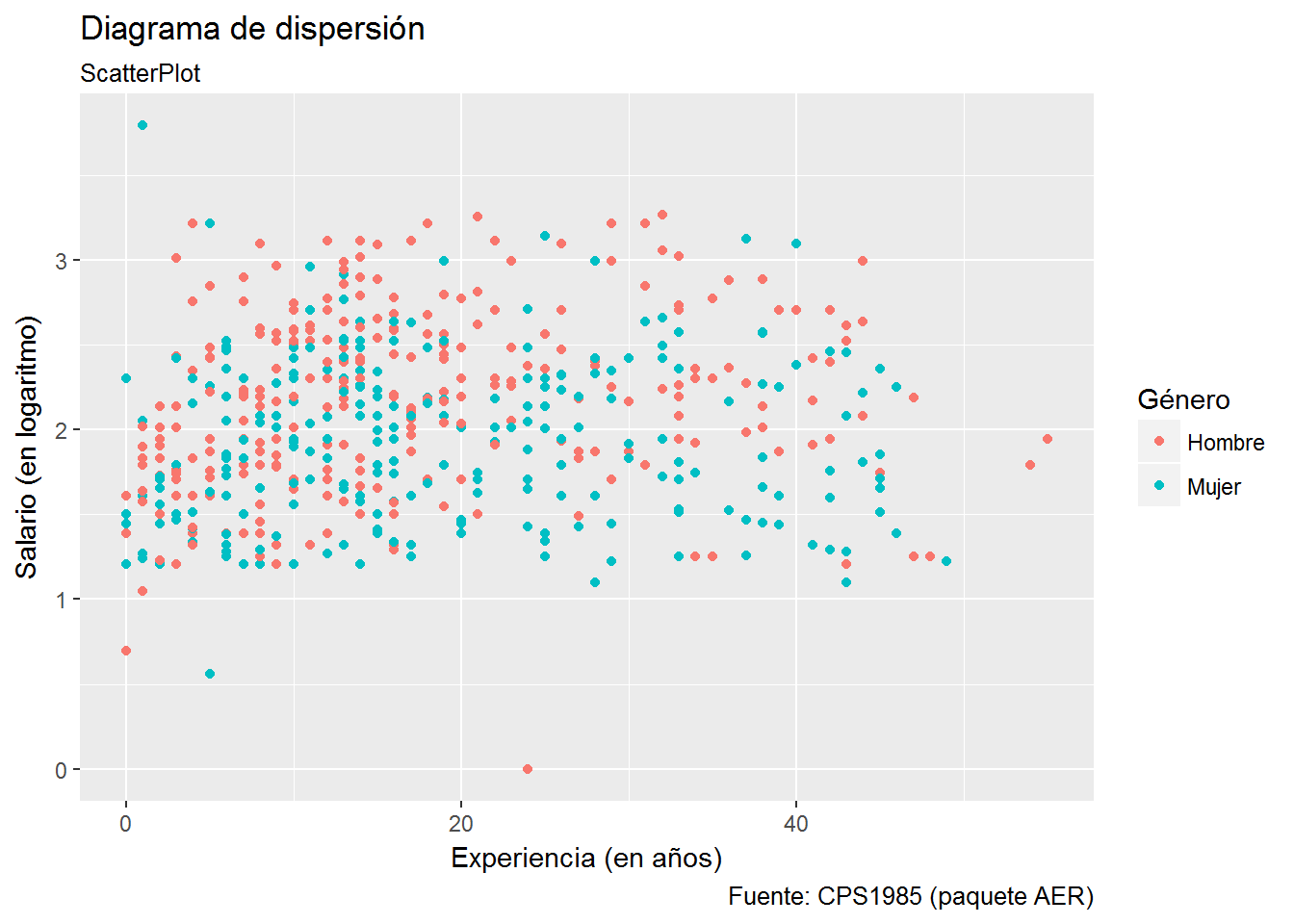 Como comentamos anteriormente, aparentemente no hay diferencias entre los dos gráficos, pero fijémonos qué sucede si añadimos la recta de regresión. Esto último lo vamos a hacer añadiendo la geometría geom_smooth() y especificando como método de estimación lm (linear model).
Como comentamos anteriormente, aparentemente no hay diferencias entre los dos gráficos, pero fijémonos qué sucede si añadimos la recta de regresión. Esto último lo vamos a hacer añadiendo la geometría geom_smooth() y especificando como método de estimación lm (linear model).
# Opción 1
ggplot(CPS1985, aes(experience,log(wage), color=gender)) +
geom_point() +
geom_smooth(method="lm", se=FALSE) +
labs(title="Diagrama de dispersión",
subtitle= "ScatterPlot",
caption="Fuente: CPS1985 (paquete AER)",
x="Experiencia (en años)",
y="Salario (en logaritmo)") +
scale_color_discrete("Género", labels=c("Hombre","Mujer"))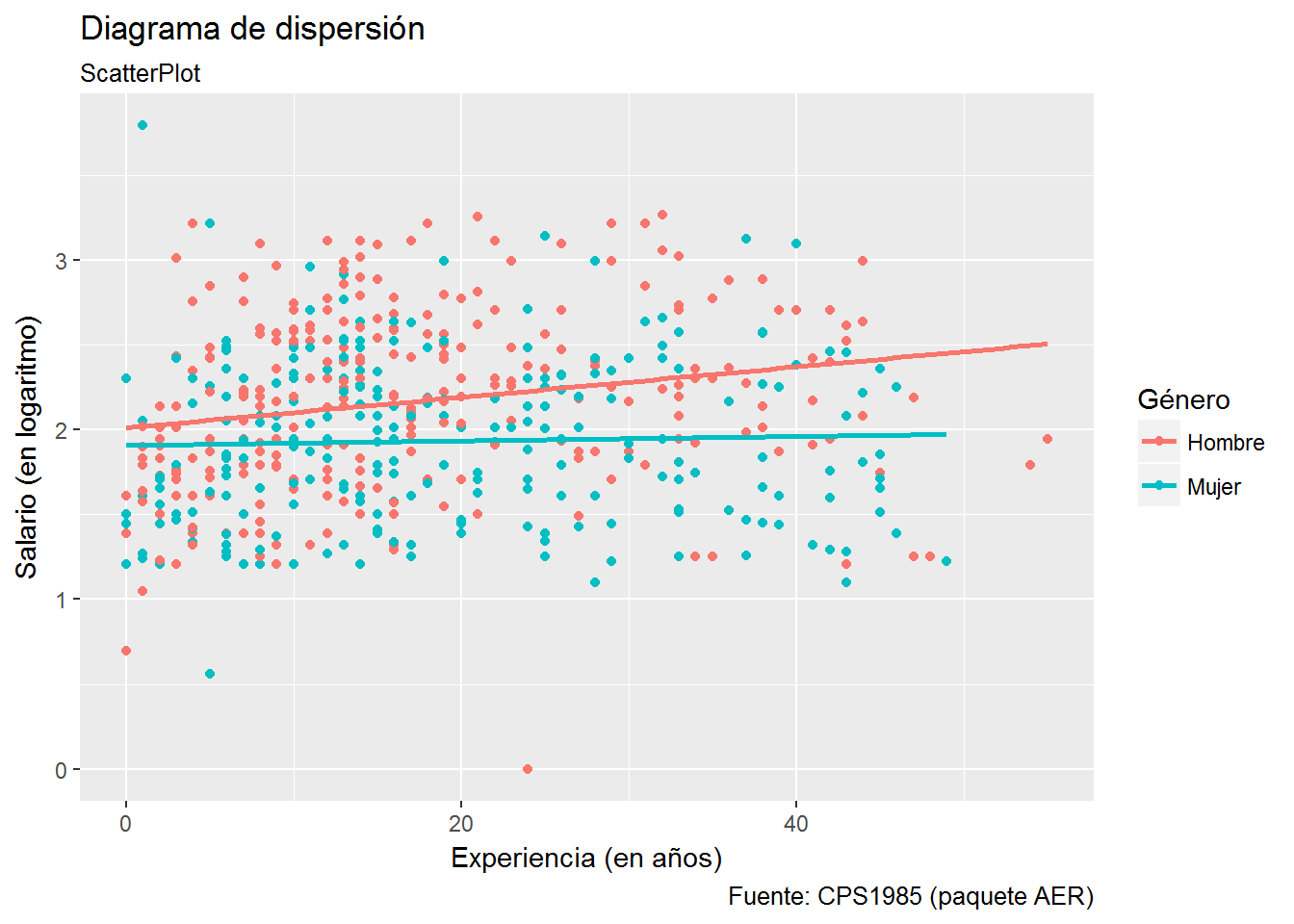
# Opción 2
ggplot(CPS1985, aes(experience,log(wage))) +
geom_point(aes(color=gender)) +
geom_smooth(method="lm") +
labs(title="Diagrama de dispersión",
subtitle= "ScatterPlot",
caption="Fuente: CPS1985 (paquete AER)",
x="Experiencia (en años)",
y="Salario (en logaritmo)") +
scale_color_discrete("Género", labels=c("Hombre","Mujer"))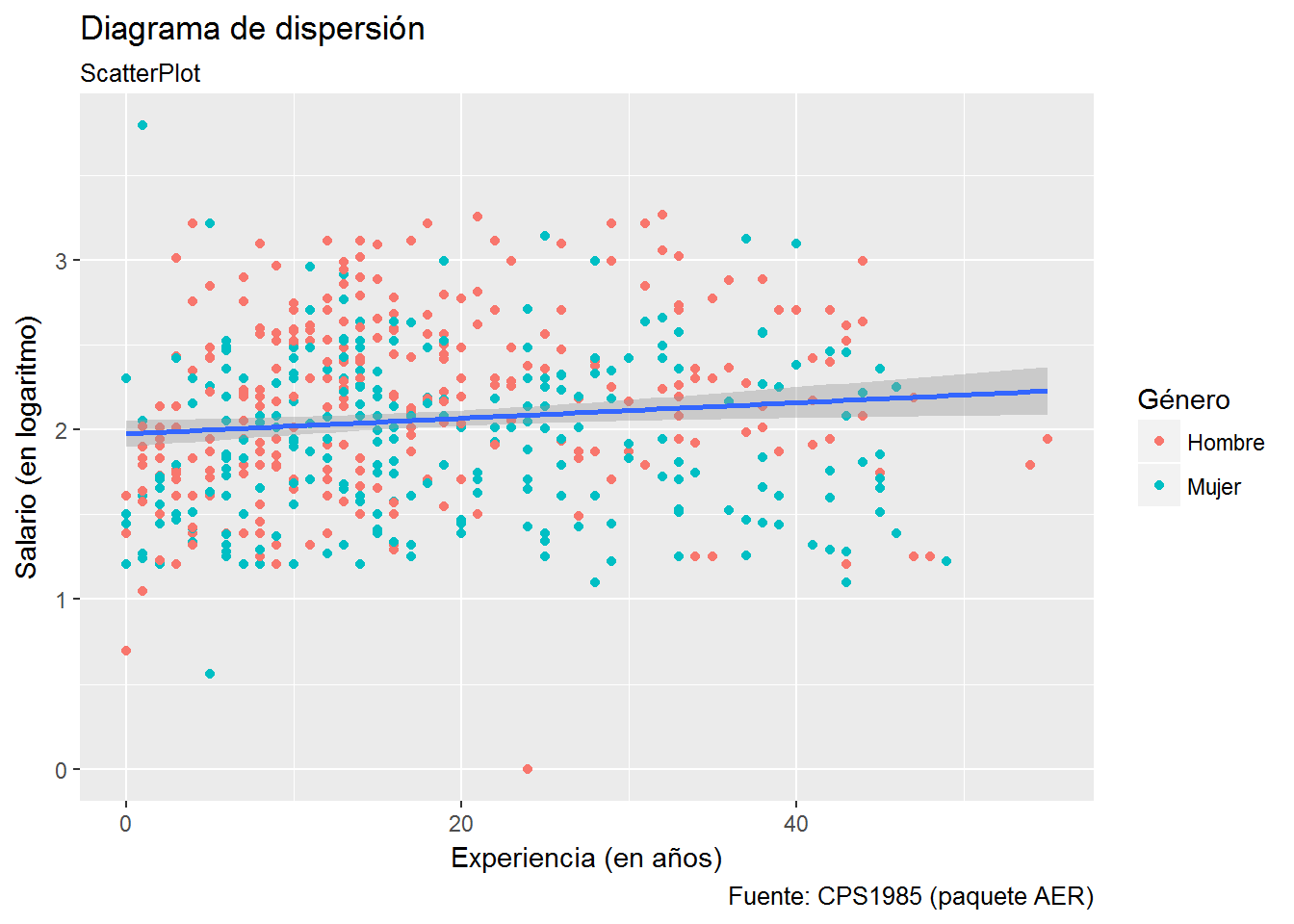
Para más detalles prácticos sobre los diagramas de dispersión podéis consultar, por ejemplo, ggplot2 scatter plots : Quick start guide - R software and data visualization o Scatterplots (ggplot2) en Cookbook for R.
Es el momento de realizar una nueva tarea…
- Tarea: Realizar un diagrama de dispersión utilizando la base de datos CPS1988 del paquete AER. Incluid en el gráfico colores según una determinada variable categórica, rectas de regresión, cambiar la posición de la leyenda y cualquier otro detalle que consideréis oportuno.
Diagramas de barras
El diagrama de barras, como ya sabemos, puede utilizarse para representar variables categóricas (atributos u ordinales) y variables cuantitativas discretas.
ggplot(CPS1985, aes(ethnicity)) +
geom_bar()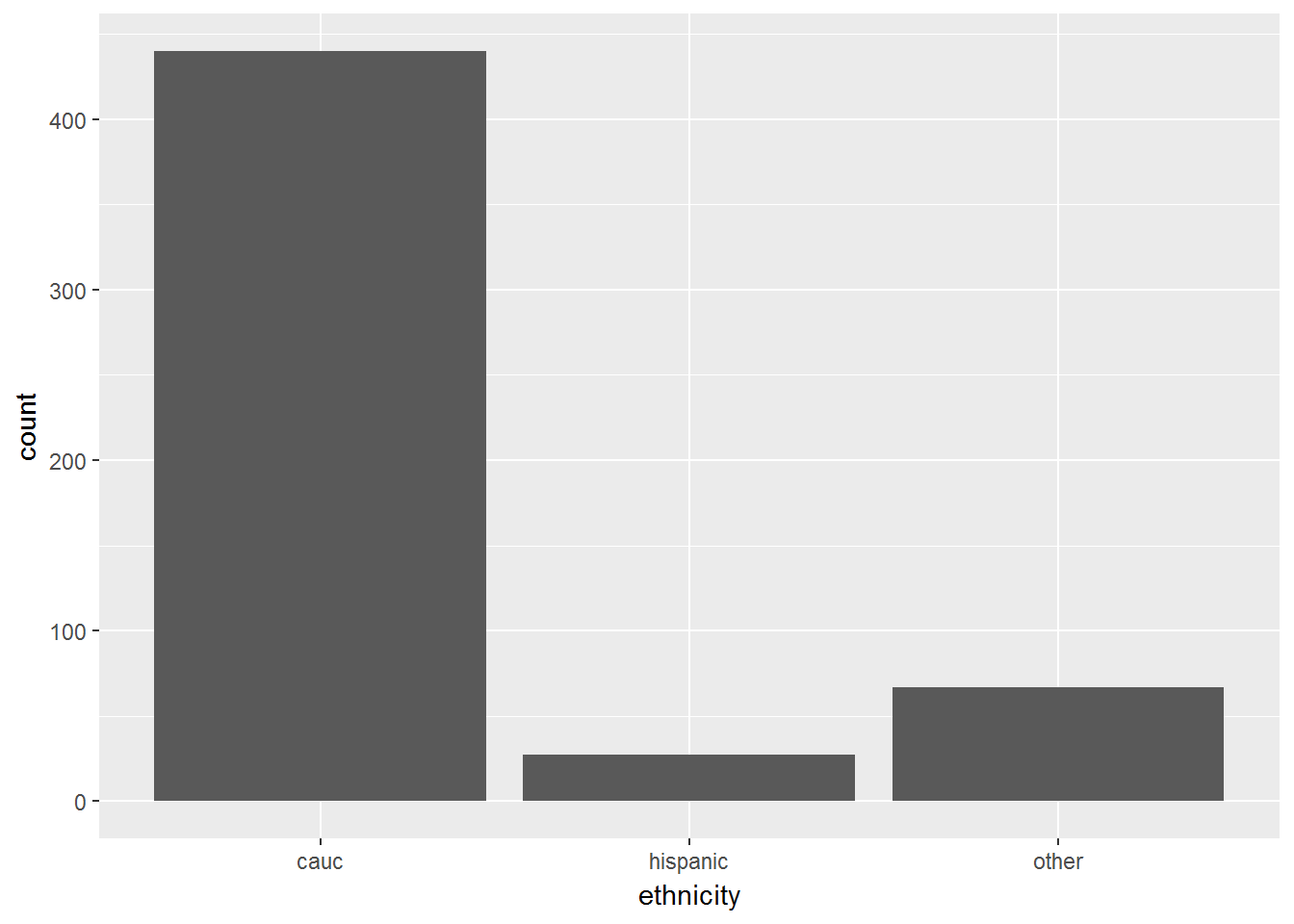
ggplot(CPS1985, aes(education)) +
geom_bar()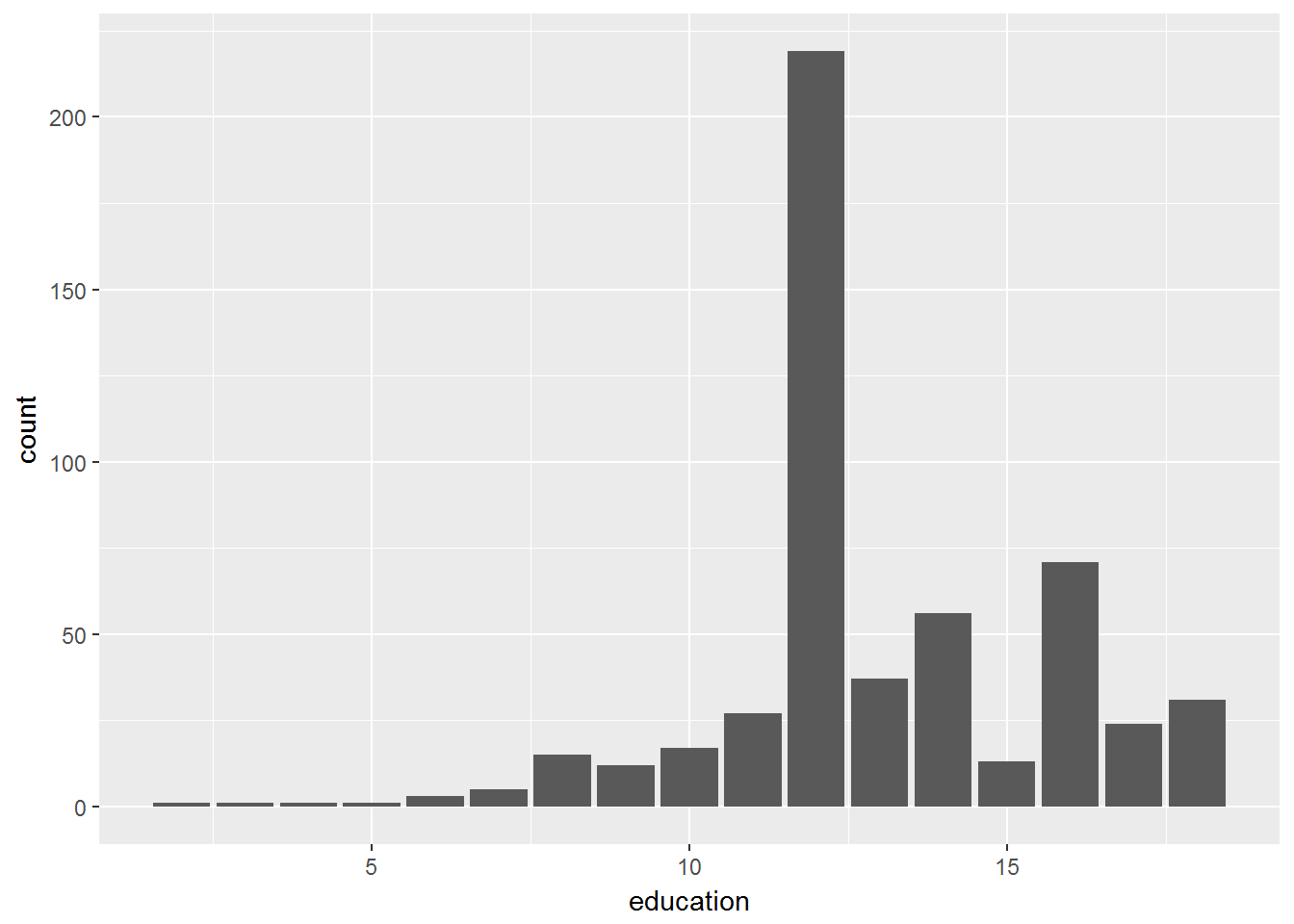
Como siempre, lo primero sería dar título al gráfico y a los ejes.
ggplot(CPS1985, aes(ethnicity)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros"))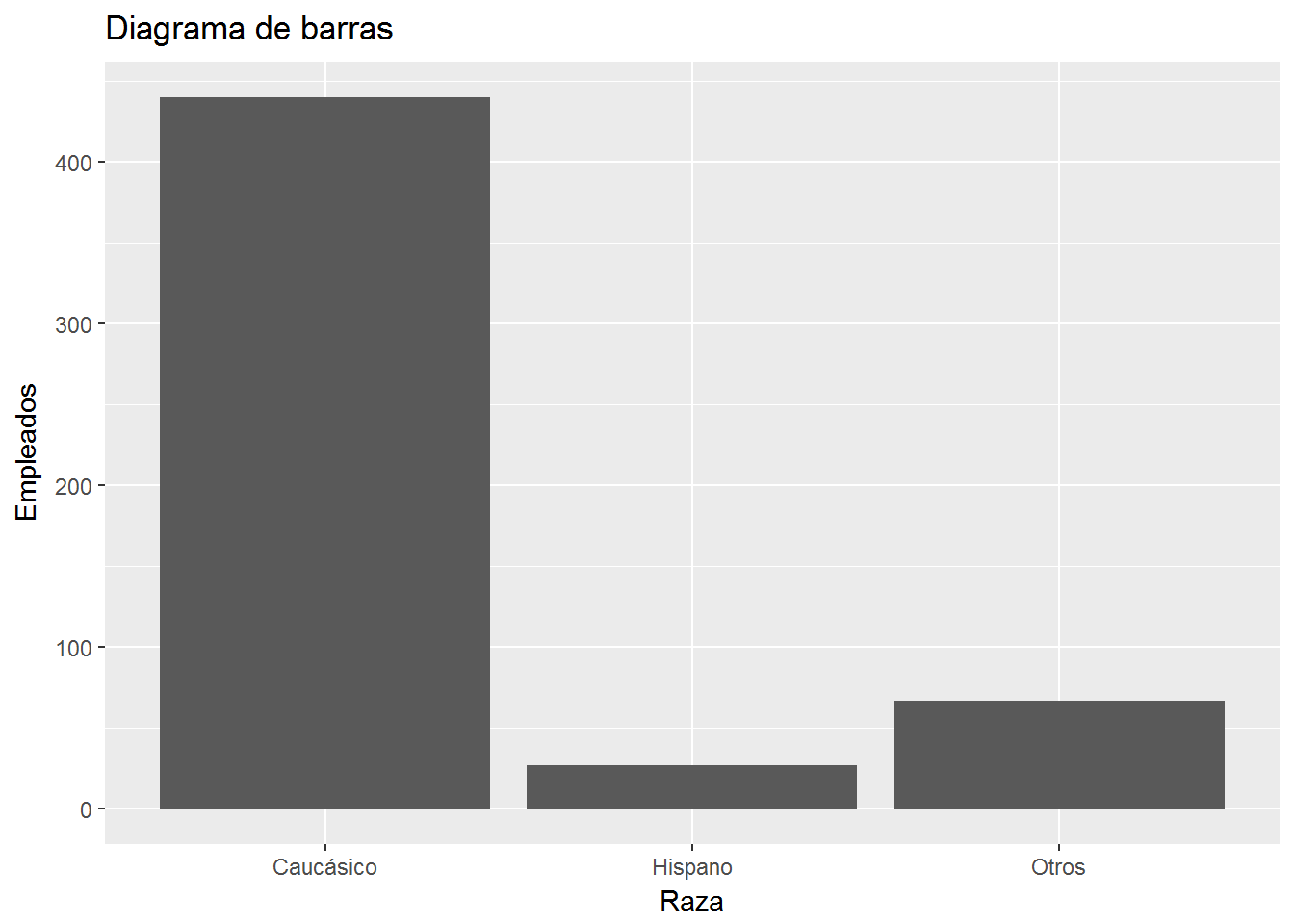
ggplot(CPS1985, aes(education)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Educación (en años)",
y="Empleados")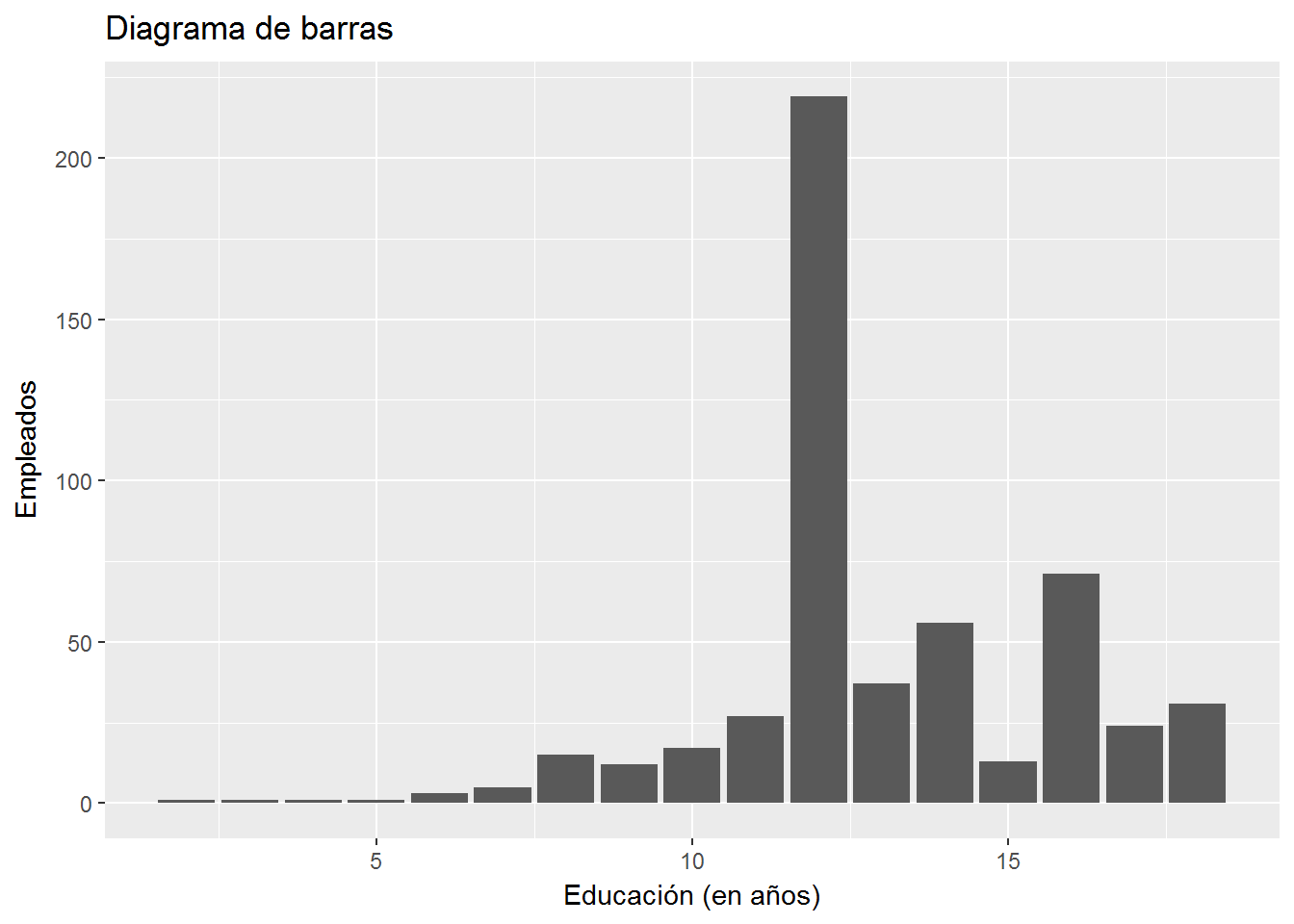
Coloreamos cada barra con un color distinto:
ggplot(CPS1985, aes(ethnicity, fill=ethnicity)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) 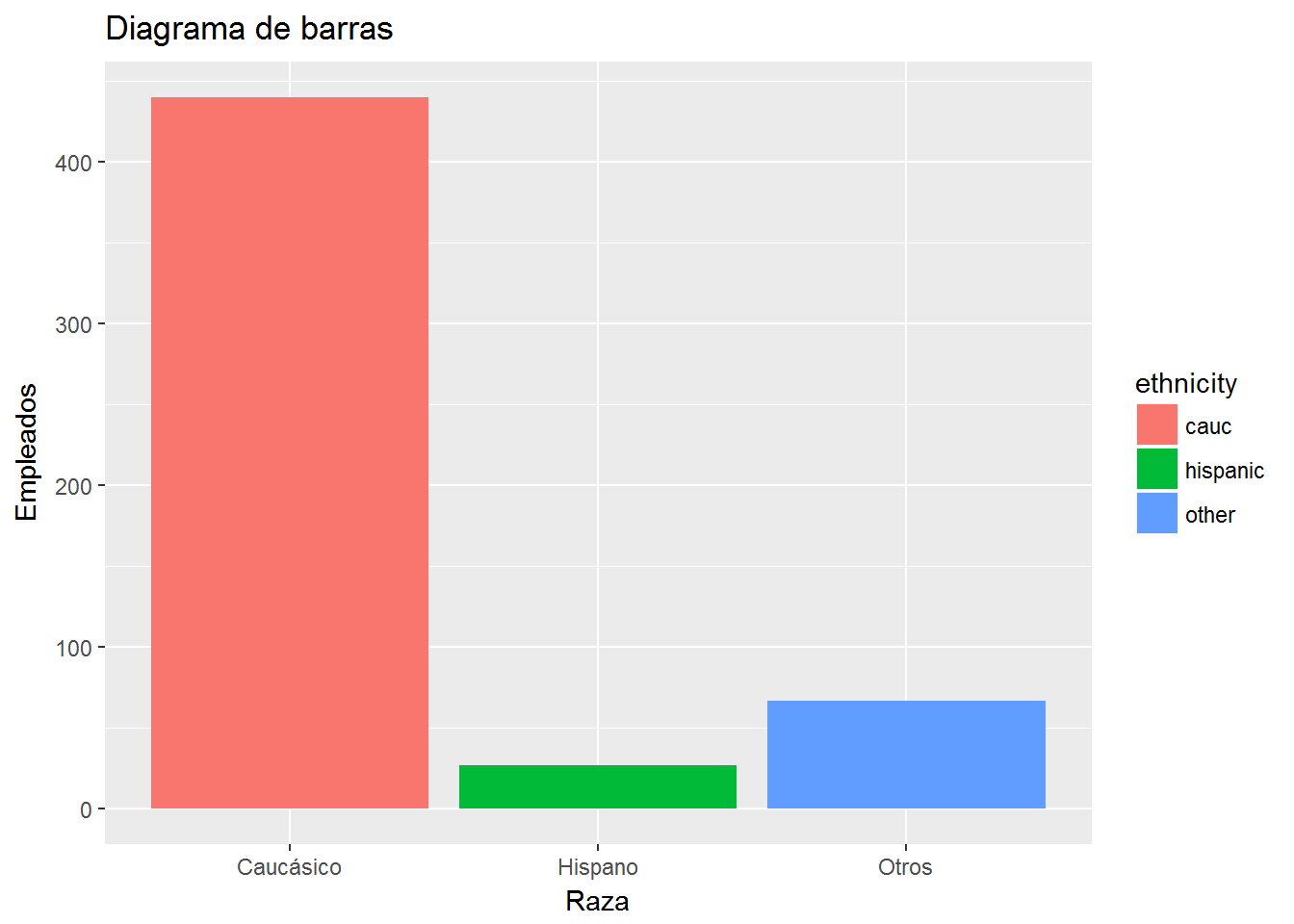
# eliminamos la leyendo porque en este caso no es ilustrativa
ggplot(CPS1985, aes(ethnicity, fill=ethnicity)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
guides(fill=FALSE)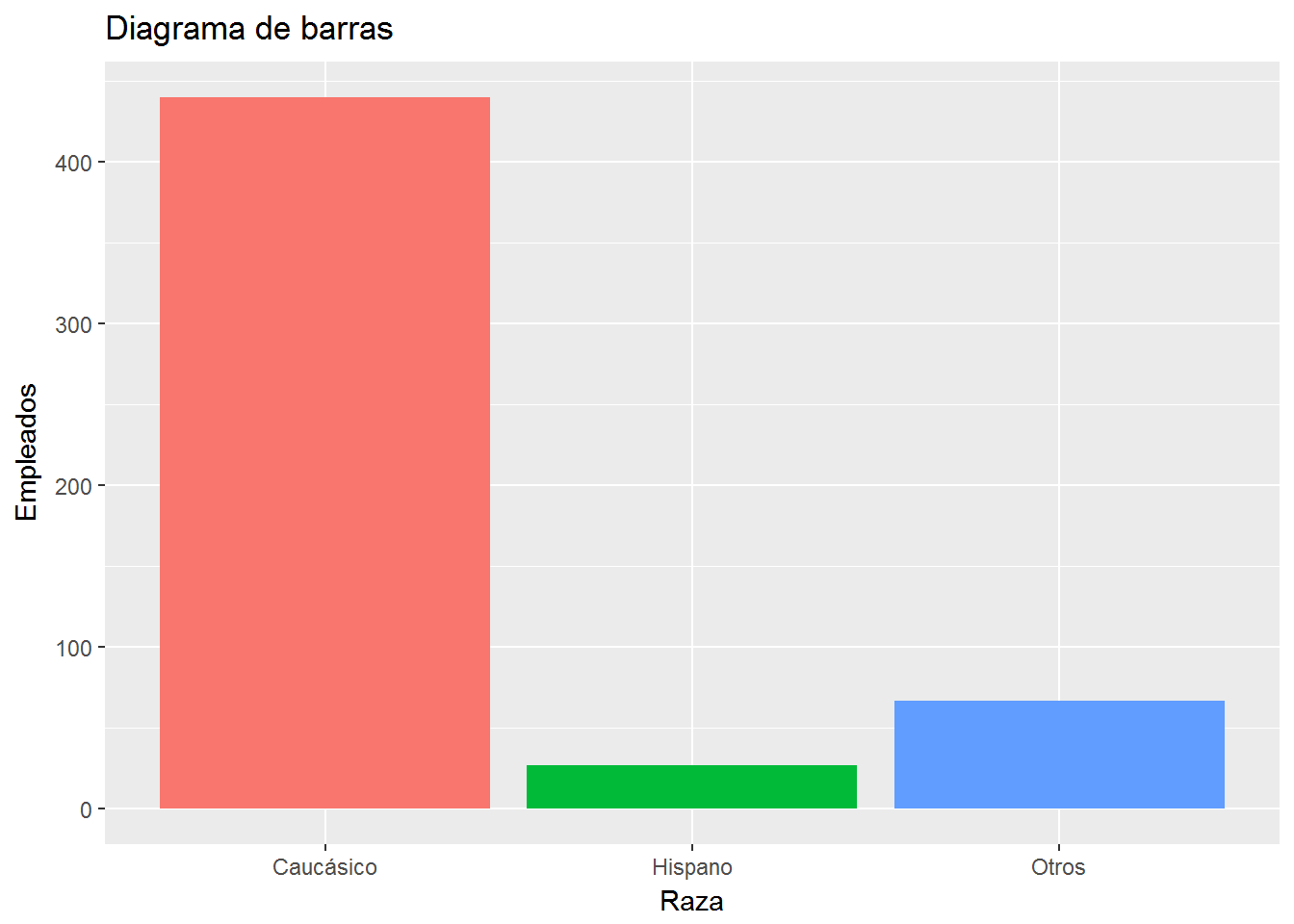
Incorporamos información sobre el número de casos en las barras correspondientes a cada categoría y eliminamos el eje Y.
ggplot(CPS1985, aes(ethnicity, fill=ethnicity)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y=NULL) +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
guides(fill=FALSE) +
geom_text(stat='count',aes(label=..count..), vjust=-0.5, size=3) 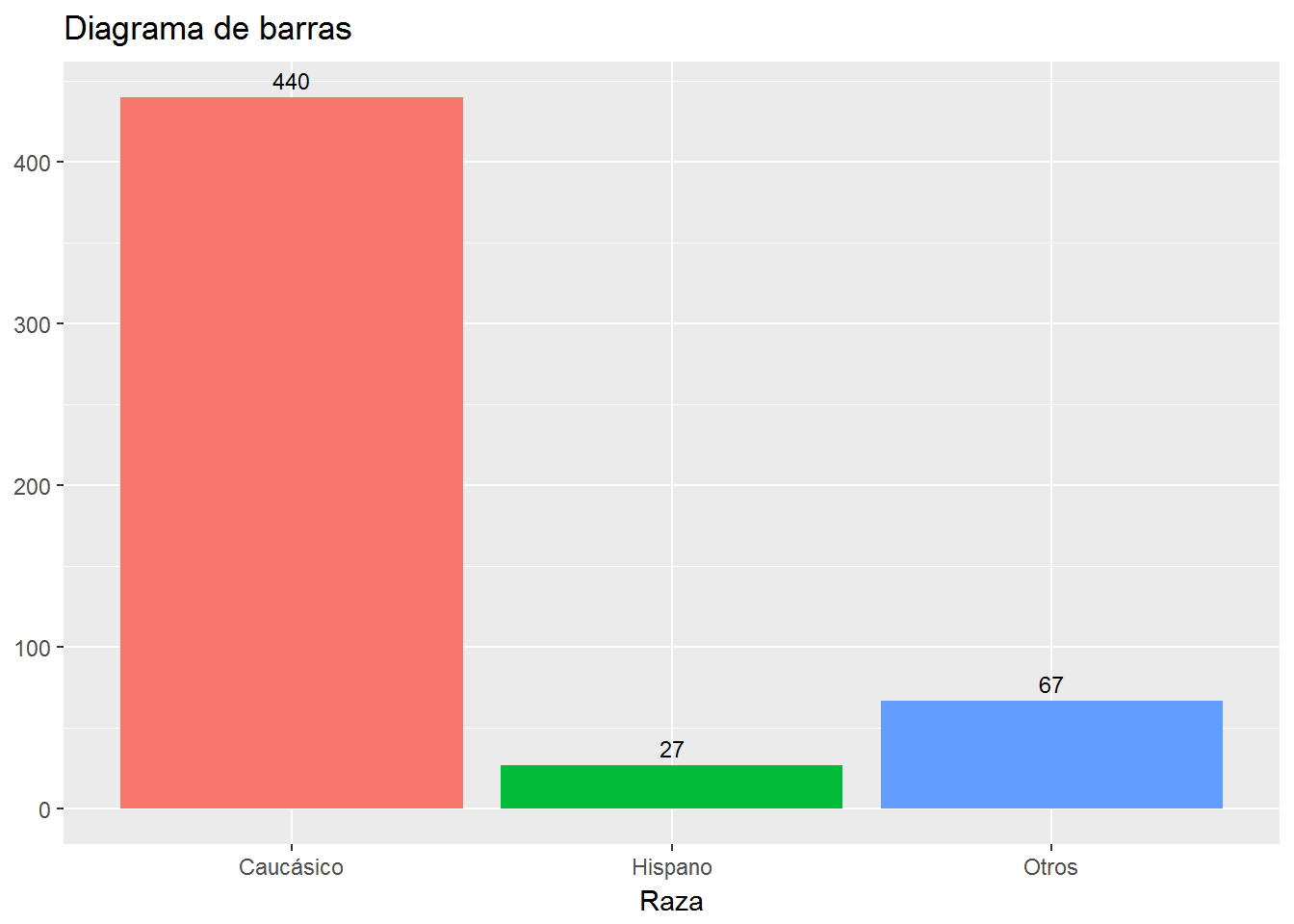 Ahora estamos interesados en ver cómo se distribuye el género según la raza.
Ahora estamos interesados en ver cómo se distribuye el género según la raza.
ggplot(CPS1985, aes(ethnicity, fill=gender)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_discrete("Género", labels=c("Hombre","Mujer"))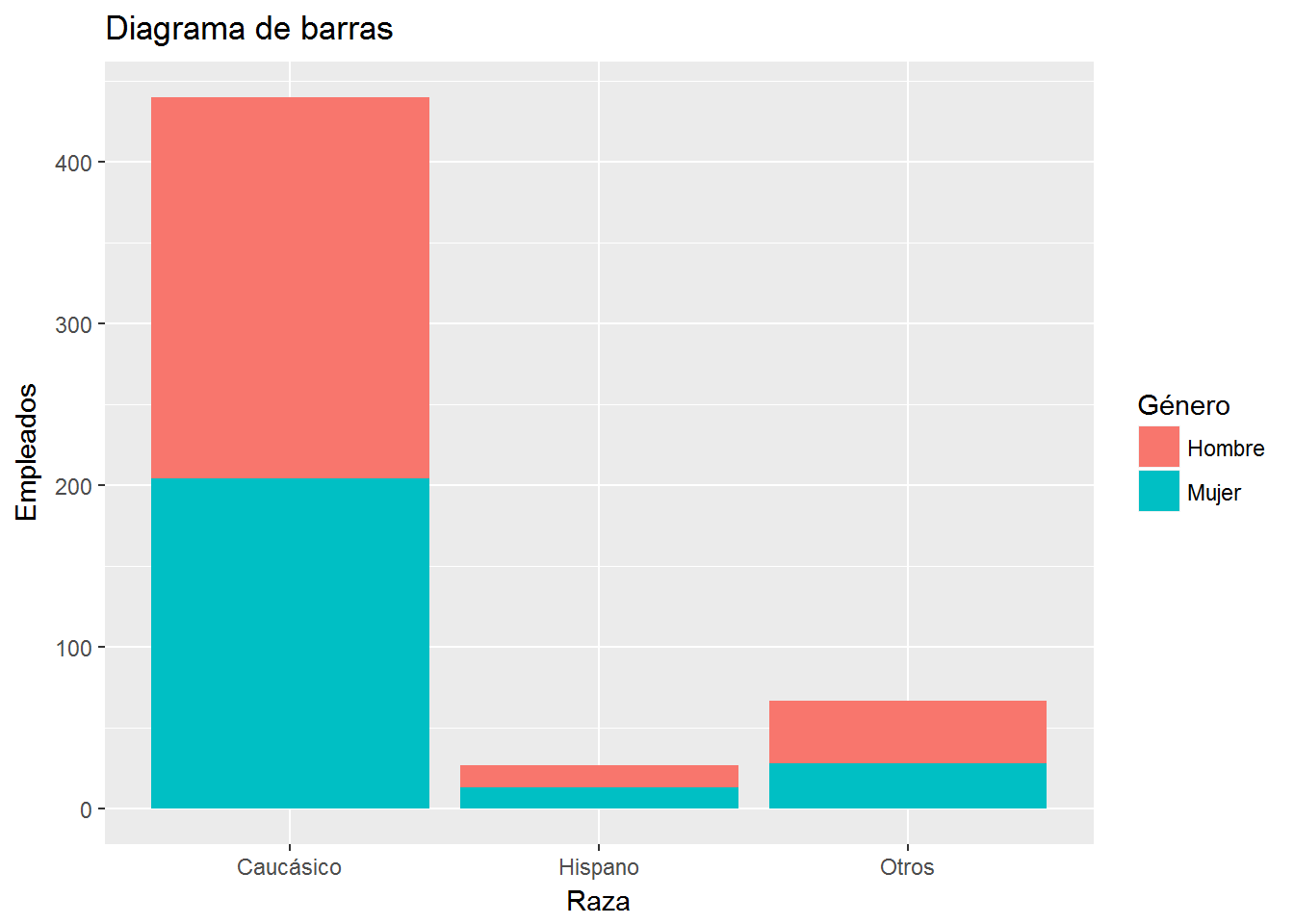
Si queremos otros colores los podemos introducir manualmente o a través de una paleta:
ggplot(CPS1985, aes(ethnicity, fill=gender)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_manual(values=c("#FF0033", "#3300FF"),
"Género",
labels=c("Hombre","Mujer"))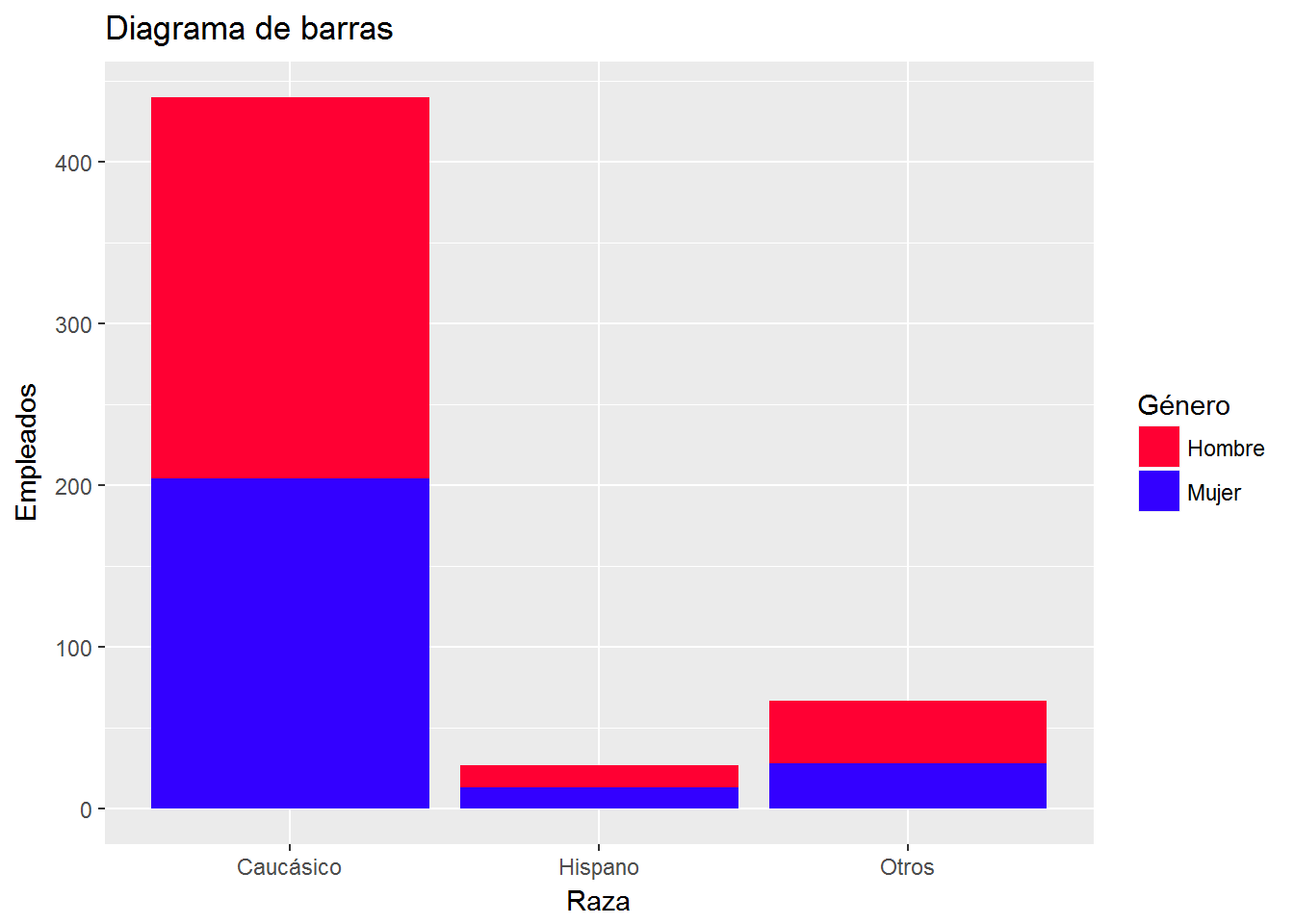
# Ejemplo 1. Paleta de colores
ggplot(CPS1985, aes(ethnicity, fill=gender)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_manual(values = heat.colors(2),
"Género",
labels=c("Hombre","Mujer"))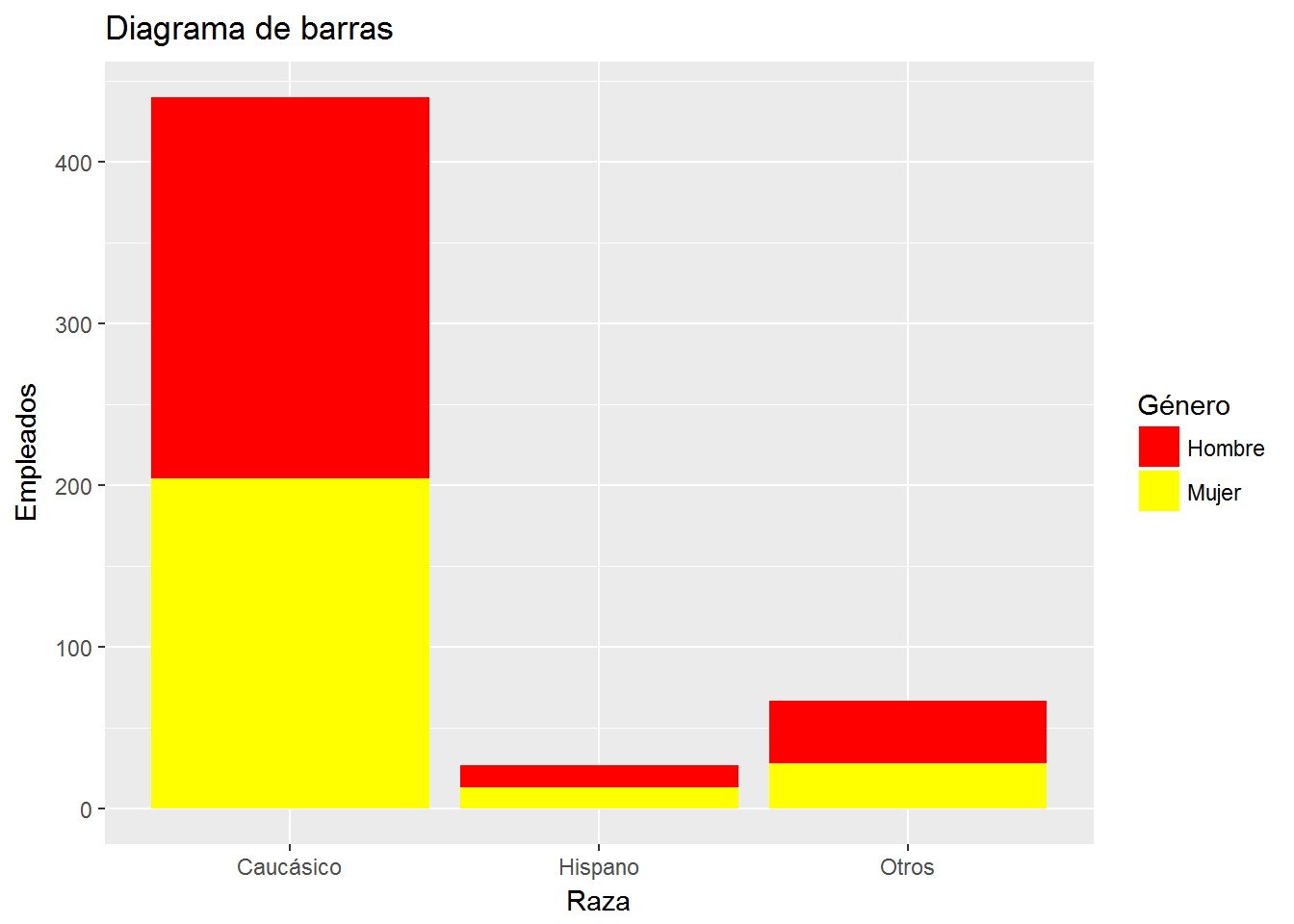
# Ejemplo 2. Paleta de colores
ggplot(CPS1985, aes(ethnicity, fill=gender)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_brewer(palette = "Accent",
"Género",
labels=c("Hombre","Mujer"))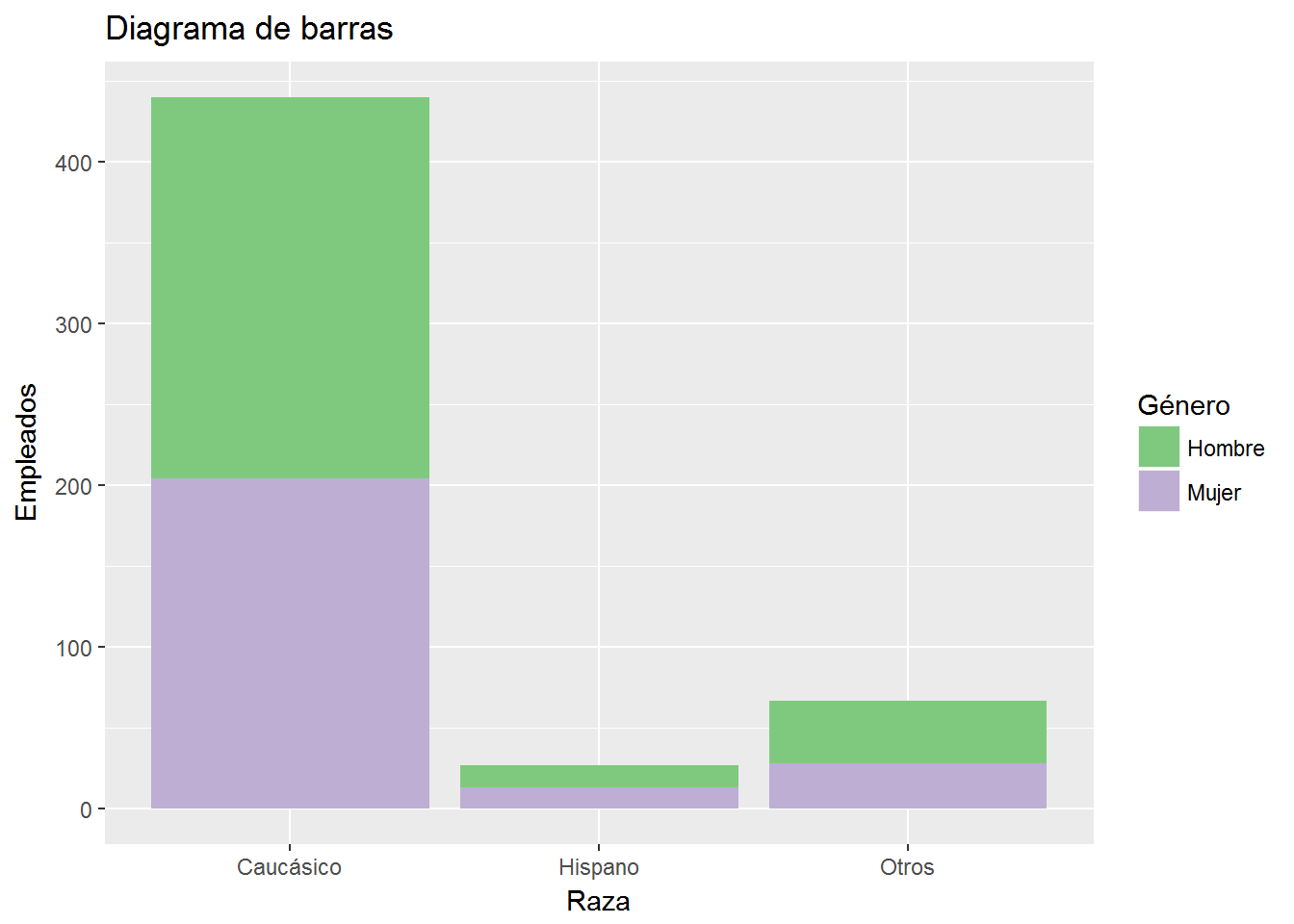 Como hicimos antes, incluimos el número de casos como parte de la información que proporciona el diagrama de barras.
Como hicimos antes, incluimos el número de casos como parte de la información que proporciona el diagrama de barras.
ggplot(CPS1985, aes(ethnicity, fill=gender)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_brewer(palette = "Accent",
"Género",
labels=c("Hombre","Mujer")) +
geom_text(stat='count',aes(label=..count..),
position = "stack",
vjust=1,
size=2,
color="red")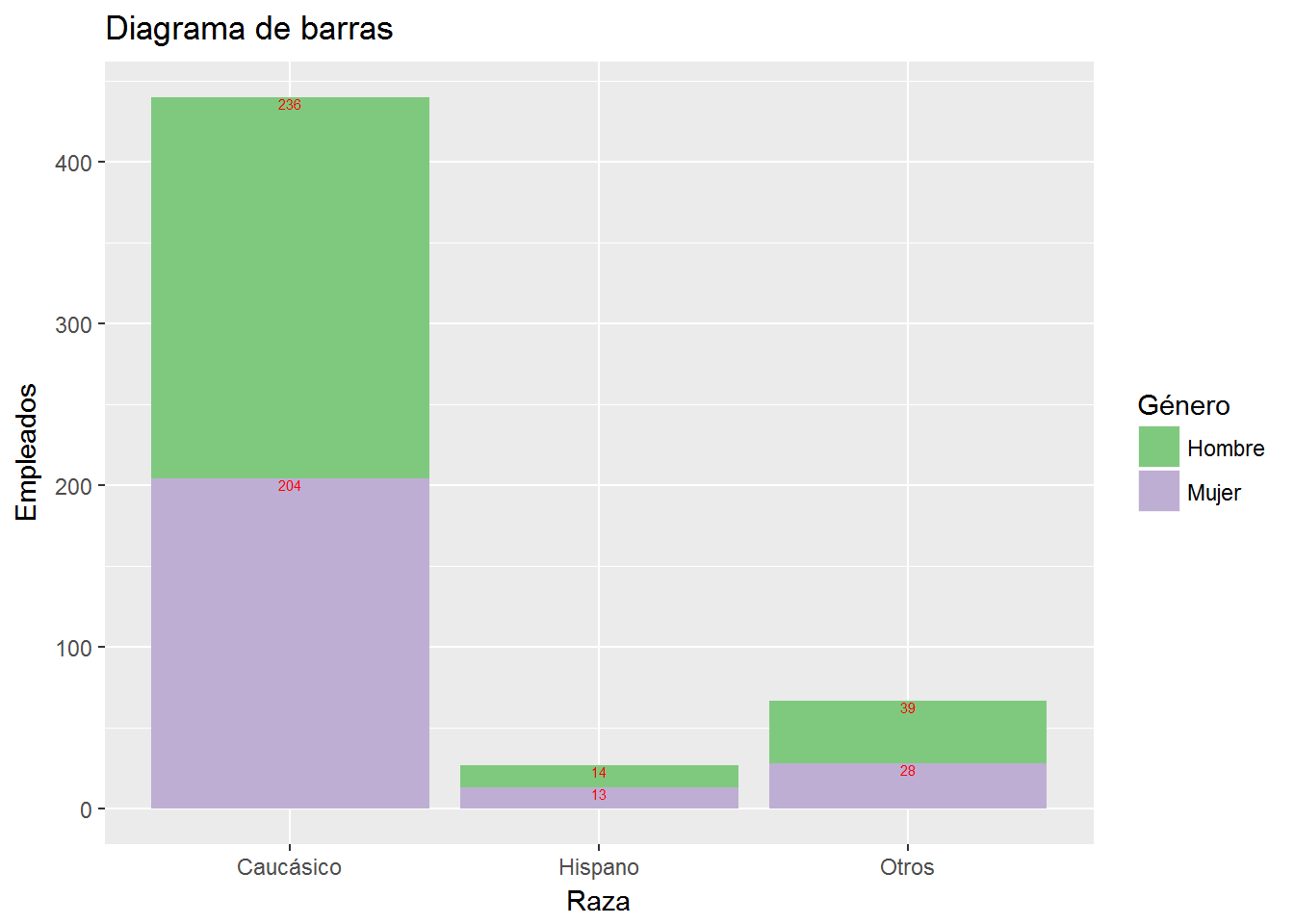
El mismo diagrama de barras apilado pero ahora en porcentajes:
ggplot(CPS1985, aes(ethnicity,y = (..count..)/sum(..count..), fill=gender)) +
geom_bar() +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_brewer(palette = "Accent",
"Género",
labels=c("Hombre","Mujer")) +
geom_text(stat="count",
aes(label = paste(round((..count..)/sum(..count..)*100), "%")),
position = "stack",
vjust=1,
size=2,
color="red")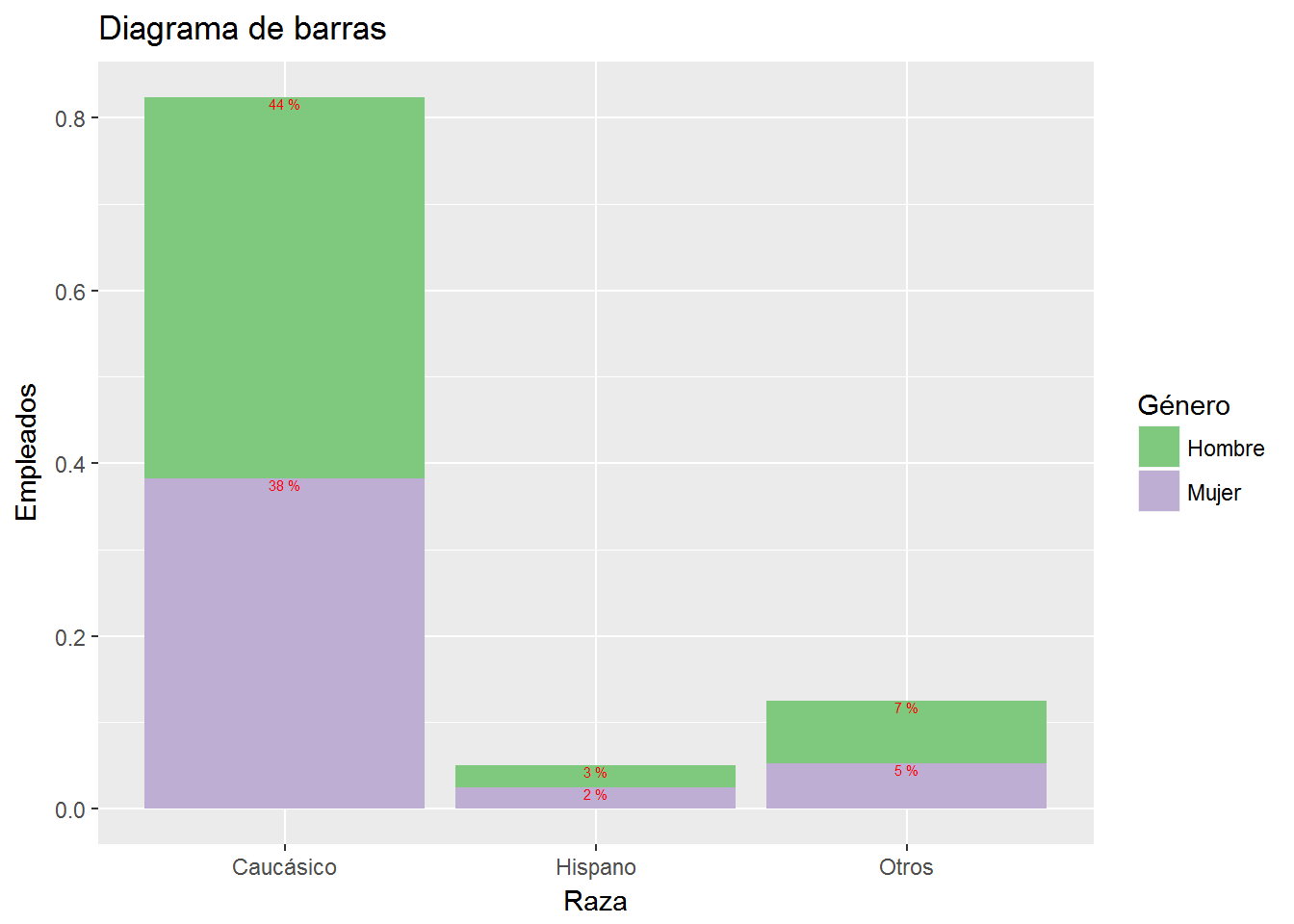
Y para ver la proporción de hombres y mujeres en cada categoría hacemos uso del parámetro position = fill dentro de la geometría.
ggplot(CPS1985, aes(ethnicity, fill=gender)) +
geom_bar(position = "fill") +
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_brewer(palette = "Accent",
"Género",
labels=c("Hombre","Mujer")) 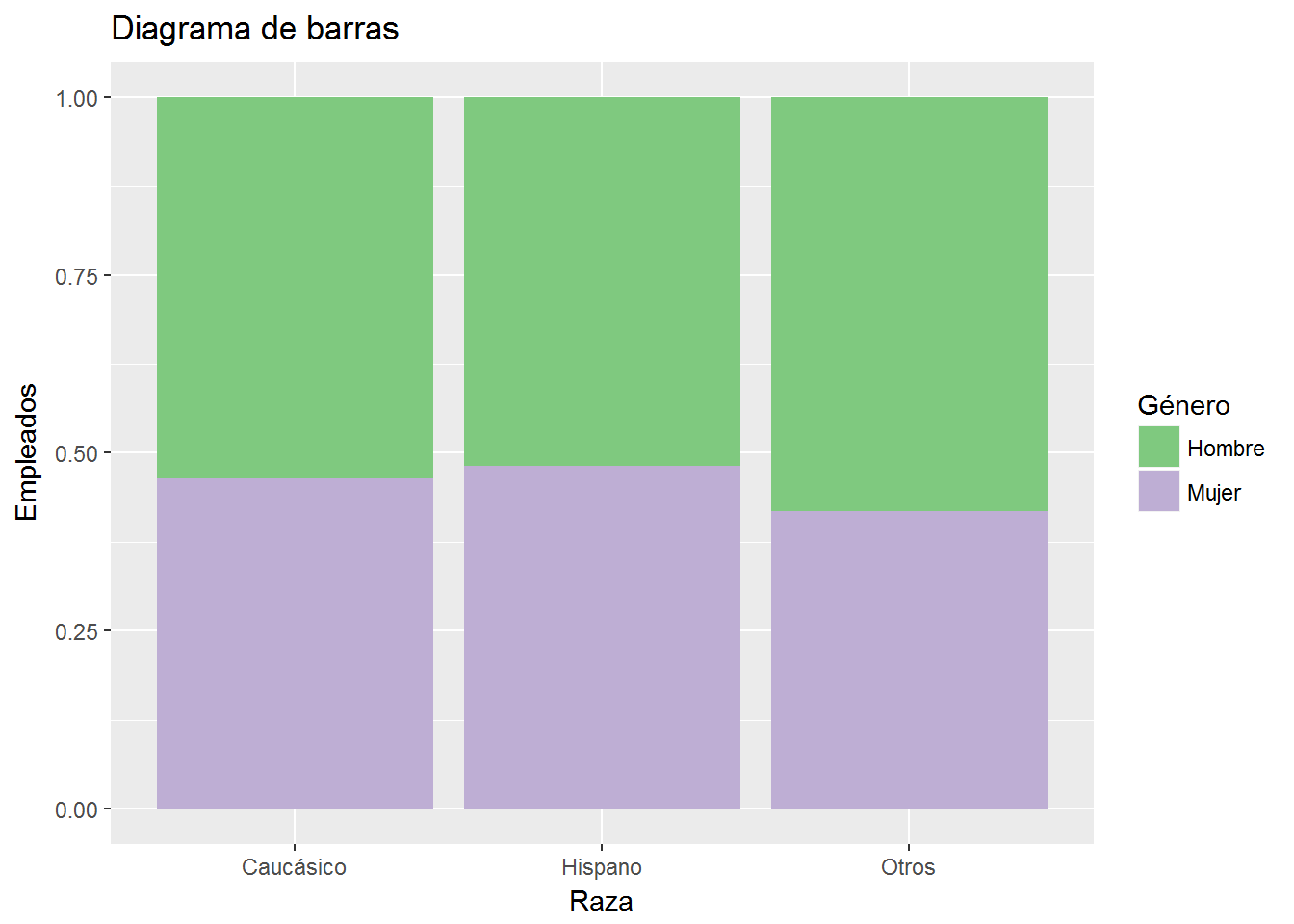
Como hemos podido comprobar hasta ahora, cuando hacemos un diagrama de barras en el que consideramos más de una variable categórica, las barras aparecen apiladas (la opción por defecto es position = “stack”). Podemos hacer que las barras se sitúen unas junto a las otras con position = “dodge”.
ggplot(CPS1985, aes(ethnicity, fill=gender)) +
geom_bar(position="dodge") + # también: position=position_dodge()
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_brewer(palette = "Accent",
"Género",
labels=c("Hombre","Mujer"))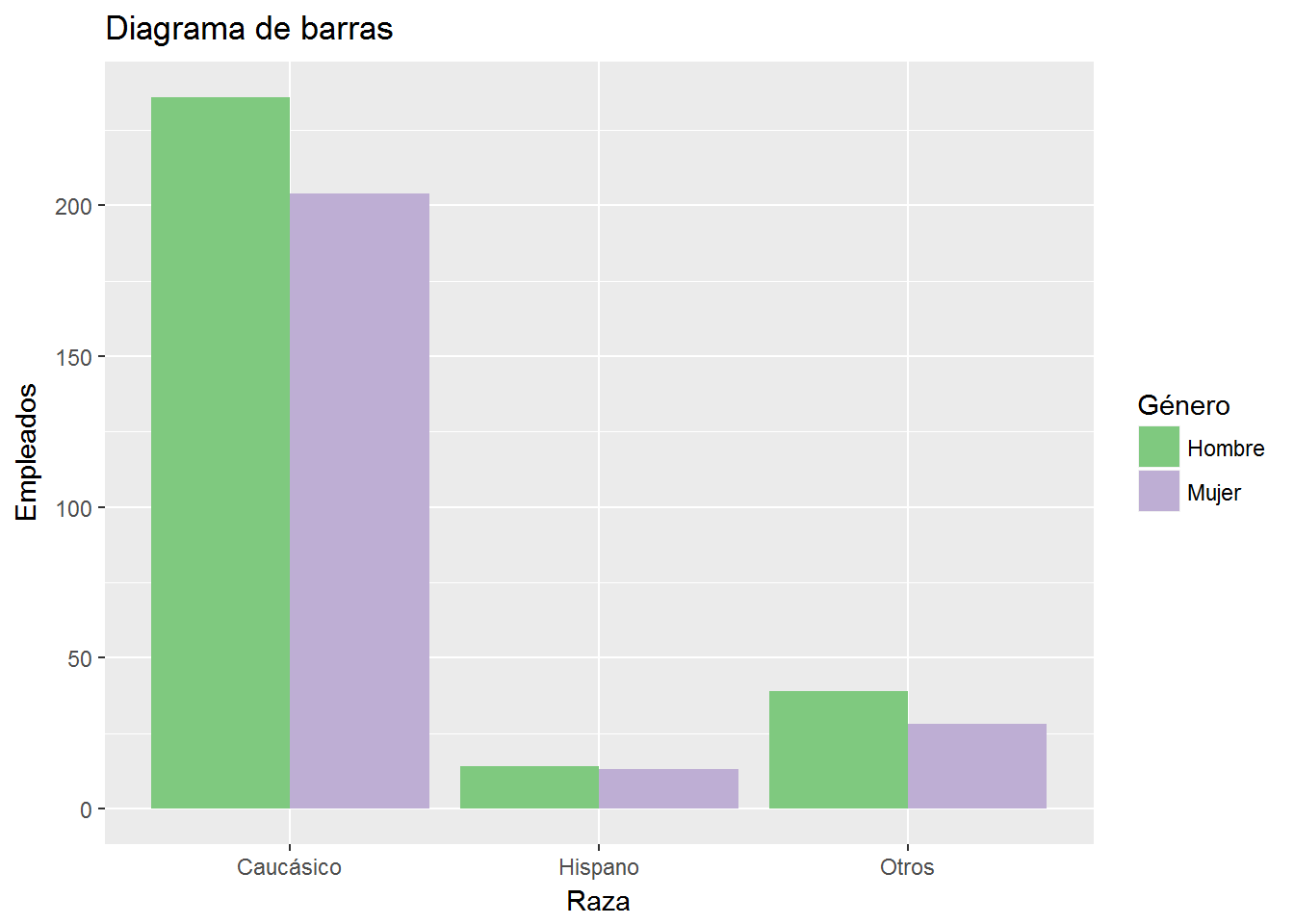
y, finalmente, podemos cambiar la orientación de las barras de vertical a horizontal.
ggplot(CPS1985, aes(ethnicity, fill=gender)) +
geom_bar(position="dodge") + # también: position=position_dodge()
labs(title="Diagrama de barras",
x= "Raza",
y="Empleados") +
scale_x_discrete(labels=c("Caucásico", "Hispano", "Otros")) +
scale_fill_brewer(palette = "Accent",
"Género",
labels=c("Hombre","Mujer")) +
coord_flip()
En R para muy principiantes encontraréis una serie de cuatro video-blogs sobre cómo elaborar un diagrama de barras en ggplot2.
5. Un ejemplo para.. “picar la curiosidad”
Para que nos hagamos una idea de las posibilidades que ofrece R, tanto en el tratamiento como en la visualización de datos, aquí os dejamos este ejemplo que aparece en la Cheat Sheet del paquete eurostat, desarrollado por Leo Lahti, Janne Huovari, Markus Kainu y Przemyslaw Biecek.
¿Qué os parece?
library(dplyr)
library(eurostat)
# Cargamos los datos de eurostat
fertility <- get_eurostat("demo_r_frate3") %>%
filter(time == "2014-01-01") %>%
mutate(cat = cut_to_classes(values, n=7, decimals=1))
mapdata <- merge_eurostat_geodata(fertility,
resolution = "20")
# Representamos los datos
ggplot(mapdata, aes(x = long, y = lat, group = group)) +
geom_polygon(aes(fill=cat), color="grey", size = .1) +
scale_fill_brewer(palette = "RdYlBu") +
labs(title="Fertility rate, by NUTS-3 regions, 2014",
subtitle="Avg. number of live births per woman",
fill="Total fertility rate(%)") +
theme_light() +
coord_map(xlim=c(-12,44), ylim=c(35,67))
6. Más referencias y sugerencias.
- R for data science.(Garrett Grolemund and Hadley Wickham)Data visualisation
- Taller de gráficos de María Elvira Ferre Jaén
- Blog de David Robinson: Don’t teach built-in plotting to beginners (teach ggplot2)
- r-statistics.co de Selva Pabhakaran.
- Be Awesome in ggplot2: A Practical Guide to be Highly Effective - R software and data visualization
- Data visualization with ggplot2. Curso gratuito de Data Camp.
- ggplot2 documentation
Libros:
- ggplot2: Elegant Graphics for Data Analysis de Hadley Wickham.
- R Graphics Cookbook: Practical Recipies for Visualizing Data. de Winston Chang.
- The R Book de Michael Crawley. Texto completo en línea a través de la biblioteca de la Universitat de València aquí