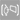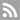Equatorial Solar and Lunar Calendar Sundial
Author: Joan Olivares
This sundial is based on the traditional equatorial model, but its operation differs: instead of the gnomon casting its shadow onto the dial, the hour figures, perforated into the equatorial ring, project sunlight onto the gnomon or central cylinder. The hours are shown using Arabic numerals, but the duodecimal system (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B) is used to maintain a symmetrical and balanced appearance. The hour indicated on the gnomon corresponds to true solar time. To read the time, one must stand with their back to the Sun and look at the centre of the illuminated area. A number will be projected onto the central cylinder together with dots (quarter hours) and stars (half hours). The solar hour is whichever number or symbol appears the brightest.
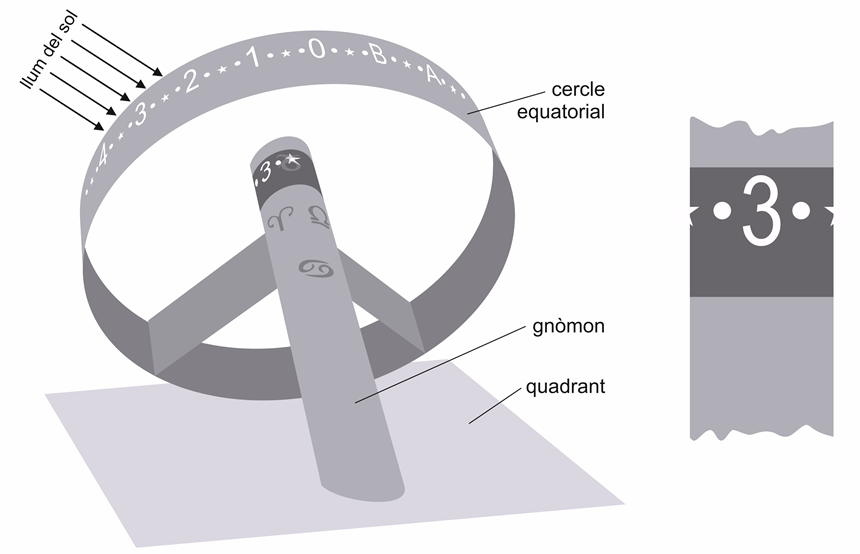
The Sun does not move across the sky at a constant speed throughout the year, as its apparent movement depends on the Earth’s motion along its elliptical orbit around the Sun. The Earth travels faster near perihelion (3 January) and more slowly near aphelion (5 July). Furthermore, the Earth’s axis of rotation is tilted relative to its orbital plane, causing true solar time to flow faster around the equinoxes than around the solstices.
These variations mean that true solar hours are not all of equal length throughout the year. For this reason, the concept of mean sun was introduced—a fictitious Sun that travels along the celestial equator at a constant speed, enabling us to measure mean solar time. A similar measure is Universal Time Coordinated (UTC), used to establish global time zones, based on the Greenwich meridian. In València, civil time is UTC+1, and during summer, one additional hour is currently applied.
The difference between true solar time and mean solar time is known as the equation of time (see the graph).
As this sundial is not located exactly on the Greenwich meridian but 0.42° west of it, a delay of 1 minute and 41 seconds must be corrected for.
How can I calculate civil time from the sundial solar time?
Civil time = Sundial solar time – Equation of time + 1 min 41 sec + 1 hour + (an extra 1 hour in summer if seasonal time change applies)
Calendar
Throughout the year, the projection zone of the hour figures shifts across the central cylinder according to the Sun’s position.
• Upper section (Capricorn): winter solstice (21 December).
• Central section (Aries and Libra): spring (21 March) and autumn (22 September) equinoxes.
• Lower section (Cancer): summer solstice (21 June).
The figure besides the sundial shows the shadow cast on the winter solstice (21 December) at three o’clock.
Moon
The sundial includes a representation of the lunar phases located at various positions around the equatorial cylinder. To read the time by moonlight, one must visually estimate the Moon’s phase and identify it with one of the lunar markers. The position of this marker will correspond to midnight, meaning that when the image of that phase appears projected on the central cylinder it will indicate midnight. Other hours must be calculated by adding or subtracting the number of hours separating this phase from the full moon, which is located at the top of the dial.
Examples:
On a full moon, the lunar phase mark will be found at twelve (12).
The difference between the phase and twelve is 12–12 = 0 hours.
The correction is zero, so the time indicated by moonlight will match the (night-time) solar time.
On a day when the Moon is exactly at last quarter, the lunar phase will be found at six in the morning.
The difference between the phase and twelve is 12–6 = 6 hours.
The correction is 6 hours. Thus, to obtain the (night-time) solar time, 6 hours must be added to the time indicated by moonlight.