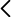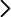- Varillas finas de madera (también podrían ser espaguetis)

- Anillos, pie de rey, regla

Descripción

Conceptos de corrientes volumétrica y superficial:

- En electromagnetismo, la densidad de corriente eléctrica volumétrica J se define como una magnitud vectorial cuyo módulo proporciona la corriente por unidad de área transversal. Se dice volumétrica porque está repartida en el volumen del conductor, aunque se toma como referencia la sección que atraviesa. Sus unidades en el SI son A/m² . En el caso de una corriente distribuida uniformemente en la sección A de un conductor, la relación entre la corriente I y la densidad de corriente volumétrica J viene dada por:

I = J·A     igualmente, J = I / A

- Hay ocasiones en que la corriente fluye, no distribuida en el volumen del conductor, sino por una parte superficial de él, de grosor despreciable (efecto piel).

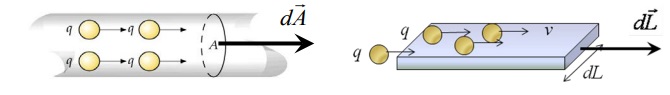
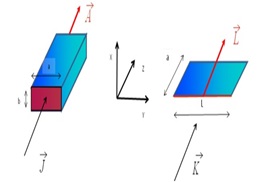
- Se define entonces la densidad de corriente superficial K como una magnitud vectorial cuyo módulo proporciona la corriente por unidad de longitud transversal atravesada. Sus unidades en el SI son A/m. En el caso de una corriente distribuida uniformemente en la longitud transversal L de una lámina conductora de grosor despreciable, la relación entre la corriente I y la densidad de corriente superficial K viene dada por:

I = K·L     igualmente, K = I / L

Densidad de corriente volumétrica representada por varillas:

Supondremos que las varillas finas representan líneas de corriente eléctrica y que cada una de ellas transporta una corriente de, por ejemplo, de 1 mA (valor arbitrario). Como son todas iguales, podemos suponer que equivalen a una densidad de corriente uniforme. Si introducimos las varillas dentro de un anillo, simularemos una densidad de corriente volumétrica que atraviesa la sección del anillo.

Densidad de corriente volumétrica representada por varillas:

Supondremos que las varillas finas representan líneas de corriente eléctrica y que cada una de ellas transporta una corriente de, por ejemplo, de 1 mA (valor arbitrario). Como son todas iguales, podemos suponer que equivalen a una densidad de corriente uniforme. Si introducimos las varillas dentro de un anillo, simularemos una densidad de corriente volumétrica que atraviesa la sección del anillo.

Disponemos de un anillo de sección transversal A conocida (midiendo el diámetro). Podemos determinar la densidad de corriente volumétrica J contando el número N de varillas que caben en esa sección y dividiendo por el valor de la sección transversal: J = N varillas(mA) / A (cm² ).

Conocida la densidad de corriente volumétrica, podemos saber la corriente que atraviesa un anillo problema, si medimos su sección transversal. La corriente que lo atraviesa será la densidad de corriente volumétrica determinada anteriormente multiplicada por el área del anillo problema: I(problema) = J·A(problema). Este valor debería de coincidir con el número de varillas que caben en el anillo problema.

Densidad de corriente superficial K representada por varillas:

Continuando con el símil de las varillas, una densidad superficial será un conjunto de varillas distribuidas sobre una superficie, de tal manera que su altura es de tan sólo una varilla.

Al igual que antes, podemos determinar la densidad de corriente superficial K que atraviesa una cierta longitud transversal conocida (en este caso, una regla), contando las varillas y dividiendo por la longitud transversal que ocupan.

Si caben N varillas en una longitud transversal L, la densidad de corriente superficial K será: K = N varillas(mA) / L(cm).

Conocida la densidad de corriente superficial, podemos saber la corriente que atraviesa una longitud problema, colocándola transversalmente a las varillas anillo problema. La corriente que atraviesa la longitud problema será la densidad de corriente superficial determinada anteriormente multiplicada por la longitud: I(problema) = K·L(problema). Este valor debería de coincidir con el número de varillas que ocupan la longitud problema.

Repetir las medidas con diferentes secciones problema y diferentes longitudes problema