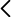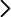Tarjetas y soportes para tarjetas
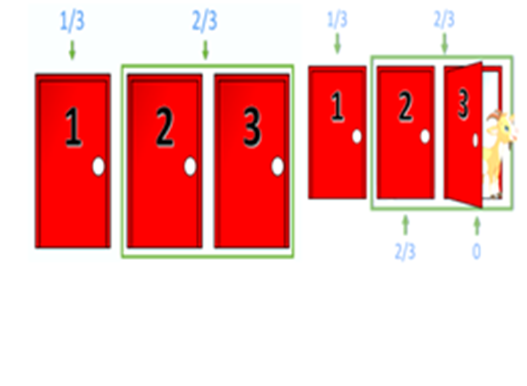
El problema de Monty Hall es un famoso dilema matemático de probabilidad que se basa en un escenario hipotético inspirado en el concurso televisivo estadounidense “Let’s Make a Deal”. La situación es la siguiente: Imagina que estás en un concurso y tienes que elegir entre tres puertas cerradas. Detrás de una de ellas hay un coche y detrás de las otras dos, hay sendas cabras (como ejemplo de premio sin valor). Escoges una puerta, por ejemplo, la número 1. El presentador, que sabe lo que hay detrás de cada puerta, abre otra puerta, digamos la número 3, revelando siempre una cabra (es decir, la única puerta con cabra si la que has elegido esconde una cabra o una aleatoria entre las dos posibilidades que habría si has elegido la puerta del coche). Luego te ofrece la oportunidad de cambiar tu elección inicial por la otra puerta cerrada, la número 2. La pregunta es: ¿Deberías mantener tu elección original o cambiar a la otra puerta? ¿Aumentan tus probabilidades de ganar el coche si cambias de puerta? La respuesta (para algunos) contraintuitiva es que sí deberías cambiar de puerta. Al principio, la probabilidad de que el coche esté detrás de la puerta que elegiste es de 1/3, y la probabilidad de que esté detrás de una de las otras dos puertas es de 2/3. Cuando el presentador abre una puerta que tiene una cabra, la probabilidad de 2/3 no cambia, pero ahora se concentra en la única puerta que queda cerrada. Por lo tanto, cambiar de puerta duplica tus posibilidades de ganar el coche a 2/3. Este problema ha generado mucho debate y confusión porque desafía la intuición de muchas personas, pero matemáticamente, cambiar de puerta es la estrategia que maximiza tus posibilidades de ganar [1]. En esta demostración se propone realizar el experimento repetidas veces para mostrar cuál es la mejor estrategia acumulando suficiente estadística. Existen también sitios web donde se puede hacer dicha simulación [2]. Mucha gente razona que da igual cambiar o no, ya que la probabilidad de acertar es del 50% en cada una, pero eso solo sería cierto para el caso en el que el jugador eligiera después de abrir una de las puertas.
Para poder realizar muchas pruebas in situ, se utilizan tres tarjetas plastificadas que se pueden colocar sobre soportes (los numerados del 1 al 3). En cada tarjeta hay una puerta por un lado y un coche o una cabra por el otro. Hay más tarjetas con cabras para una prueba que se explicará después. El procedimiento es el siguiente:
1) Se elige un “secretario” que saldrá a la pizarra para apuntar cuáles van siendo los resultados (es decir, si cada estudiante-concursante se lleva el coche o no) 2) Se pregunta a los alumnos si se quedarían con la puerta inicial, si cambiarían o si piensan que da igual. Se hacen así dos grupos, uno con los que cambiarían y otro con los que no cambiarían o piensan que da igual. Alternativamente se pueden incluir a los que piensan que da igual en el otro grupo si así se consiguen grupos más parejos en número. Esta clasificación se hace previamente para evitar que conforme vean lo que eligen los compañeros anteriores o el resultado de las pruebas, acaben todos eligiendo lo mismo. 3) Se lleva a cabo el concurso con cada uno de los estudiantes (primero para uno de los grupos anteriores, luego para el otro, para facilitar el conteo por parte del secretario). En cada prueba el profesor baraja las cartas, colocándolas en el soporte de manera que muestren a los alumnos las puertas. El alumno elige una puerta, el profesor “abre” una de las otras dos que no tiene cabra y el alumno cambia su elección o no según haya elegido estar en el grupo de los que cambian o no. El secretario apunta si acierta o no con su “elección” final. 4) Para asegurar que hay suficiente estadística, se pueden hacer varias rondas para cada uno de los grupos, de manera que al final se tengan unos 30 casos al menos en ambos grupos, mejor si son 40. Una forma para que los alumnos vean de manera más intuitiva que lo mejor es cambiar es plantear el experimento con 10 puertas, con solo un premio. En ese caso es más evidente que si elegimos una puerta al azar y el presentador abre 8 puertas sin premio, lo más razonable es cambiar de puerta porque claramente la probabilidad de haber acertado en nuestra primera elección es muy baja (10%). Esta prueba se puede realizar con los soportes y tarjetas adicionales (hay también una tarjeta extra de reemplazo).
Se puede comentar que es un problema que se menciona en varios elementos de cultura popular, por ejemplo: El problema fue popularizado por Marilyn vos Savant en su columna de la revista Parade Magazine en 1990, lo que llevó a un amplio debate público sobre la solución correcta. Esta historia se menciona en la novela “El curioso incidente del perro a medianoche”, de M. Haddon. También aparece en la película “21 blackjack”, dirigida por R. Luketic, o en episodios de las series Friends, Broklyn Nine-Nine o The Hollow
[1] https://es.wikipedia.org/wiki/Problema_de_Monty_Hall [2] https://www.mathwarehouse.com/monty-hall-simulation-online/