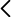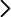Sistema de ejes coordenados en acero. Sistema de ejes coordenados con vector (en acero) aplicado en 0 y desplazable. Producto vectorial con módulo realista (vector producto extensible).
Descripción El sistema de ejes coordenados de la Figura 1 permite visualizar las coordenadas o componentes cartesianas de un punto en 3 dimensiones. Las componentes (X, Y, Z) de un punto sobre los tres ejes coordenados (), que se cortan en el origen del sistema coordenado O, representan las dimensiones de alto, ancho y profundidad del punto en el espacio real tridimensional.

Figura 4. Los ejes coordenados (x,y,z) están representados por los vectores unitarios ()
Dado un punto A con componentes (Ax, Ay, Az) en el espacio real tridimensional, el sistema de ejes coordenados nos permite representar, con dirección al punto, el vector que une el origen del sistema coordenado O y el propio punto. Este sistema de ejes coordenados, formado por tres vectores, (
), unitarios (de módulo unidad) y linealmente independientes y que permiten generar o representar cualquier vector del espacio real tridimensional, forma una base del espacio vectorial real tridimensional (Figura 4). El sistema de ejes coordenados de la Figura 2 también nos permite visualizar la proyección (o la sombra) de un vector sobre cualquiera de los tres ejes coordenados o sobre el plano definido por dos de ellos (Figura 5). La barra con flecha (vector) tiene movimiento en dirección azimutal y polar. Permite visualizar también los ángulos que el vector forma con el eje z y el plano XY. También los ángulos que la proyección sobre el plano XY forma con el eje x e y.

Figura 5. Izquierda: el vector forma un ángulo 𝜃1 con el eje coordenado S. La proyección de
en la dirección de S es un vector de módulo
. Derecha: la proyección de 𝐴⃗ sobre el plano ZX viene dada por el vector
Dados dos vectores, 𝐴⃗ y , en un espacio vectorial tridimensional, su producto vectorial,
, da como resultado un vector perpendicular a ellos y, por lo tanto, normal al plano que los contiene (imagen izquierda de la Figura 6). Para determinar la dirección del vector resultante se suele usar la regla de la mano derecha: la dirección del dedo pulgar de la mano derecha indica la dirección del vector resultante del producto vectorial, 𝐶⃗=
, mientras que los dedos índice y corazón representan, respectivamente, los vectores
(imagen izquierda de la Figura 6).

Figura 6. Producto vectorial de dos vectores. Izquierda: dirección del vector resultante y regla de la mano derecha. Derecha: área del paralelogramo definido por los vectores que se multiplican.

A su vez, el módulo del producto vectorial de dos vectores, ||, coincide con el área del paralelogramo definido por los vectores que se multiplican (imagen derecha de la Figura 6). En este sentido, en el montaje de la Figura 3 la antena se alarga de forma que representa, de manera realista, el módulo del producto vectorial de los vectores que se multiplican (ver Figura 7).
Figura 7.